Buckling and Free Vibrations of Nanoplates—Comparison of Nonlocal Strain and Stress Approaches
Abstract
:1. Introduction
2. Formulation of the Problem
2.1. Kinematic Relations
2.2. Constitutive Nonlocal Equations and Variational Formulation
- local stress theory
- local strain theoryrepresents the classical 2-D Laplacian operator.
- the nonlocal stress theory
- the nonlocal strain theorywhere is the local stress tensor, is the stiffness matrix and is an operator.
3. The Rayleigh-Ritz Method
- the nonlocal stress theory
- the nonlocal strain theorywhere λ is the Rayleigh quotient.
4. Numerical Results and Discussion
4.1. Buckling Loads–Uniform, Uni-Axial Compression along the x-axis ()
4.1.1. Nonlocal Stress Theory
- CPT:
- FSDT and HSDT:The determinant of the coefficient matrix derived from Equation (20) must be equal to zero, i.e.,:
4.1.2. Nonlocal Strain Theory
- CPT:
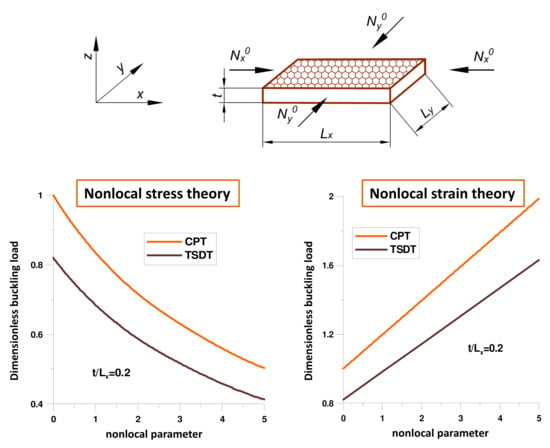
- FSDT and HSDT:The fundamental relations for FSDT or HSDT can be derived in a similar manner as in the previous section. Since they are more complicated as for the nonlocal stress theory, we do not demonstrate them in the explicit form. Instead of, we show the effects in the form of graphs plotted in Figure 5. In general, the nonlocal strain theory leads to the growth of buckling loads in comparison with the nonlocal stress theory (Figure 4). The increase factor is equal to . Those effects are identical to the reported in the literature by Lim et al. [14] for beams.
4.2. Free Vibrations
- the nonlocal stress theory:
- the nonlocal strain theory:
5. Conclusions and Future Works
- The description of the displacements with the use of the third order polynomial or exponential approximations leads to the identical results.
- The first order shear deformation theory seems to be a good approximation; the use of the higher order shear deformation theory can be necessary as transverse shear effects are significantly enhanced by the low values of the Gxz/E and Gyz/E ratios.
- In the strain or stress nonlocal problems, the evaluation of eigenvalues is reduced to the operation of division/multiplication by the identical factor; therefore two different physical formulations have different effects on the searched values understood in the sense of weakening or enhancement the buckling/vibration effects in comparison with the classical global approach.
Author Contributions
Funding
Conflicts of Interest
References
- Peddieson, J.; Buchanan, G.R.; McNitt, R.P. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Lu, P.; Zhang, P.Q.; Lee, H.P.; Wang, C.M.; Reddy, J.N. Non-local elastic plate theories. Proc. R. Soc. A 2007, 463, 3225–3240. [Google Scholar] [CrossRef]
- Barretta, R.; Feo, L.; Luciano, R.; Marotti de Sciarra, F. Application of an enhanced version of the Eringen differential model to nanotechnology. Compos. B 2016, 96, 274–280. [Google Scholar] [CrossRef]
- Chen, W.J.; Li, X.P. Size-dependent free vibration analysis of composite laminated Timoshenko beam based on new modified couple stress theory. Arch. Appl. Mech. 2013, 83, 431–444. [Google Scholar] [CrossRef]
- Wang, Q. Wave propagation in carbon nanotubes via nonlocal continuum mechanics. J. Appl. Phys. 2005, 98, 124301. [Google Scholar] [CrossRef]
- Ma, H.M.; Gao, X.L.; Reddy, J.N. A non-classical Mindlin plate model based on a modified couple stress theory. Acta Mech. 2011, 220, 217–235. [Google Scholar] [CrossRef]
- Kim, J.; Żur, K.K.; Reddy, J.N. Bending, free vibration, and buckling of modified couples stress-based functionally graded porous micro-plates. Compos. Struct. 2019, 209, 879–888. [Google Scholar] [CrossRef]
- Barretta, R.; Feo, L.; Luciano, R.; Marotti de Sciarra, F. An Eringen-like model for Timoshenko nanobeams. Compos. Struct. 2016, 139, 104–110. [Google Scholar] [CrossRef]
- Hu, Y.G.; Liew, K.M.; Wang, Q.; He, X.Q.; Yakobson, B.I. Nonlocal shell model for elastic wave propagation in single- and double-walled carbon nanotubes. J. Mech. Phys. Sol. 2008, 56, 3475–3485. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Nonlocal bending analysis of curved nanobeams reinforced by graphene nanoplatelets. Compos. B 2019, 166, 1–12. [Google Scholar] [CrossRef]
- Arash, B.; Wang, Q. A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes. Comput. Mater. Sci. 2012, 51, 303–313. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E.C. Gradient elasticity in statics and dynamics: An overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Sol. Struct. 2011, 48, 1962–1990. [Google Scholar] [CrossRef]
- Akgoz, B.; Civalek, O. Bending analysis of FG microbeams resting on Winkler elastic foundation via strain gradient elasticity. Compos. Struct. 2015, 134, 294–301. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Barretta, R.; Canadija, M.; Marotti de Sciarra, F. Modified nonlocal strain gradient elasticity for nano-rods and application to carbon nanotubes. Appl. Sci. 2019, 9, 514. [Google Scholar] [CrossRef]
- Nowacki, W. Couple stresses in thermoelasticity. Rozprawy Inżynierskie 1968, 16, 441–471. (In Polish) [Google Scholar]
- Voigt, W. Theoretische Studien über die Elastizitatsverhaltnisse der Kristalle. Abh Koniglichen Gesellschaft Wiss Gottingen 1887, 43. [Google Scholar]
- Cosserat, E.; Cosserat, F. Théorie des corps déformables; Herman et Fils: Paris, France, 1909. [Google Scholar]
- Altenbach, J.; Altenbach, H.; Eremeyev, V.A. On generalized Cosserat-type theories of plates and shells: A short review and bibliography. Arch. Appl. Mech. 2010, 80, 73–92. [Google Scholar] [CrossRef]
- Toupin, R.A. Theory of elasticity with couple stresses. Arch. Ration Mech. Anal. 1964, 17, 85–112. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stesses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D.G.B. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Aifantis, E. On the role of gradients in the localization of deformation and fracture. Int. J. Eng. Sci. 1992, 30, 1279–1299. [Google Scholar] [CrossRef]
- Aifantis, E. Gradient deformation models at nano, micro, and macro scales. J. Eng. Mater Technol. 1999, 121, 189–202. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.M.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Rat. Mech. Anal. 1964, 16, 52–78. [Google Scholar] [CrossRef]
- Fernandez-Saez, J.; Zaera, R.; Loya, J.A.; Reddy, J.N. Bending of Euler-Bernoulli beams using Eringen’s integral formulation: A paradox resolved. Int. J. Eng. Sci. 2016, 99, 107–116. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; Marotti de Sciarra, F. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Aifantis, E. On the microstructural origin of certain inelastic models. J. Eng. Mater. Technol. 1984, 106, 326–330. [Google Scholar] [CrossRef]
- Altan, S.; Aifantis, E. On the structure of the mode III crack-tip in gradient elasticity. Scripta Metall. Mater. 1992, 26, 319–324. [Google Scholar] [CrossRef]
- Aifantis, E. Strain gradient interpretation of size effects. Int. J. Fract. 1999, 95, 299–314. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M. Micromorphic continua: Non-redundant formulations. Contin. Mech. Thermodyn. 2016, 28, 1659–1670. [Google Scholar] [CrossRef]
- Barbagallo, G.; Madeo, A.; d’Agostino, M.V.; Abreu, R.; Ghiba, I.-D.; Neff, P. Transparent anisotropy for the relaxed micromorphic model: Macroscopic consistency conditions and long wave length asymptotics. Int. J. Sol. Struct. 2017, 120, 7–30. [Google Scholar] [CrossRef]
- Neff, P.; Madeo, A.; Barbagallo, G.; d’Agostino, M.V.; Abreu, R.; Ghiba, I.-D. Real wave propagation in the isotropic-relaxed micromorphic model. Proc. R. Soc. A 2017, 473, 20160790. [Google Scholar] [CrossRef]
- Sourki, R.; Hosseini, S.A. Coupling effects of nonlocal and modified couple stress theories incorporating surface energy on analytical transverse vibration of a weakened nanobeam. Eur. Phys. J. Plus 2017, 132, 184. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Pradhan, S. Buckling of single layer graphene sheet based on nonlocal elasticity and higher order shear deformation theory. Phys. Lett. A 2009, 373, 4182–4188. [Google Scholar] [CrossRef]
- Pradhan, S.; Murmu, T. Small scale effect on the buckling of single-layered graphene sheets under biaxial compression via nonlocal continuum mechanics. Comput. Mater. Sci. 2009, 47, 268–274. [Google Scholar] [CrossRef]
- Pradhan, S.; Phadikar, J. Small scale effect on vibration of embedded multilayered graphene sheets based on nonlocal continuum models. Phys. Lett. A 2009, 373, 1062–1069. [Google Scholar] [CrossRef]
- Sakhaee-Pour, A. Elastic buckling of single-layered graphene sheet. Comput. Mater. Sci. 2009, 45, 266–270. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J.N. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Civalek, O.; Demir, C. Bending analysis of microtubules using nonlocal Euler–Bernoulli beam theory. Appl. Math. Model 2011, 35, 2053–2067. [Google Scholar] [CrossRef]
- Fazelzadeh, S.A.; Ghavanloo, E. Nonlocal anisotropic elastic shell model for vibrations of single-walled carbon nanotubes with arbitrary chirality. Compos. Struct. 2012, 94, 1016–1022. [Google Scholar] [CrossRef]
- Shen, Z.-B.; Tang, H.-L.; Li, D.-K.; Tang, G.-J. Vibration of single-layered graphene sheet-based nanomechanical sensor via nonlocal Kirchhoff plate theory. Comput. Mater. Sci. 2012, 61, 200–205. [Google Scholar] [CrossRef]
- Nami, M.R.; Janghorban, M. Resonance behavior of FG rectangular micro/nano plate based on nonlocal elasticity theory and strain gradient theory with one gradient constant. Compos. Struct. 2014, 111, 349–353. [Google Scholar] [CrossRef]
- Ansari, R.; Faghih Shojaei, M.; Mohammadi, V.; Gholami, R.; Darabi, M.A. Nonlinear vibrations of functionally graded Mindlin microplates based on the modified couple stress theory. Compos. Struct. 2014, 114, 124–134. [Google Scholar] [CrossRef]
- Barretta, R.; Marotti de Sciarra, F. Analogies between nonlocal and local Bernoulli–Euler nanobeams. Arch. Appl. Mech. 2015, 85, 89–99. [Google Scholar] [CrossRef]
- Sarrami-Foroushani, S.; Azhari, M. Nonlocal buckling and vibration analysis of thick rectangular nanoplates using finite strip method based on refined plate theory. Acta Mech. 2016, 227, 721–742. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Hrcek, S.; Pan, E. The nonlocal and gradient theories for a large deformation of piezoelectric nanoplates. Compos. Struct. 2017, 172, 119–129. [Google Scholar] [CrossRef]
- De Domenico, D.; Askes, H. Stress gradient, strain gradient and inertia gradient beam theories for the simulation of flexural wave dispersion in carbon nanotubes. Compos. B 2018, 153, 285–294. [Google Scholar] [CrossRef]
- Zenkour, A.M. A novel mixed nonlocal elasticity theory for thermoelastic vibration of nanoplates. Compos. Struct. 2018, 185, 821–833. [Google Scholar] [CrossRef]
- Zhu, J.; Lv, Z.; Liu, H. Thermo-electro-mechanical vibration analysis of nonlocal piezoelectric nanoplates involving material uncertainties. Compos. Struct. 2019, 208, 771–783. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; Marotti de Sciarra, F. Nonlocal strain gradient exact solutions for functionally graded inflected nano-beams. Compos. B 2019, 164, 667–674. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Rafii-Tabar, H.; Fazelzadeh, S.A. Computational continuum mechanics of nanoscopic structures. Nonlocal elasticity approaches; Springer: New York, NY, USA, 2019. [Google Scholar]
- Muc, A. Design and identification methods of effective mechanical properties for carbon nanotubes. Mater. Design 2010, 31, 1671–1675. [Google Scholar] [CrossRef]
- Muc, A. Modelling of carbon nanotubes behaviour with the use of a thin shell theory. J. Theor. Appl. Mech. 2011, 49, 531–540. [Google Scholar]
- Muc, A. Natural frequencies of rectangular laminated plates-introduction to optimal design in aeroelastic problems. Aerospace 2018, 5, 95. [Google Scholar] [CrossRef]
- Muc, A.; Chwał, M. Vibration control of defects in carbon nanotubes. Solid Mech. Appl. 2011, 30, 239–246. [Google Scholar]
- Muc, A.; Banaś, A.; Chwał, M. Free vibrations of carbon nanotubes with defects. Mech. Mech. Eng. 2013, 17, 157–166. [Google Scholar]
- Chwał, M. Free vibrations analysis of carbon nanotubes. Adv. Mater. Res. 2014, 849, 94–99. [Google Scholar]
- Chwał, M. Nonlocal analysis of natural vibrations of carbon nanotubes. J. Mater. Eng. Perform. 2018, 27, 6087–6096. [Google Scholar]
- Muc, A.; Jamróz, M. Homogenization models for carbon nanotubes. Mech. Compos. Mater. 2004, 40, 101–106. [Google Scholar] [CrossRef]
- Chwał, M.; Muc, A. Transversely isotropic properties of carbon nanotube/polymer composites. Compos. B 2016, 88, 295–300. [Google Scholar]
- Chwał, M. Deformations and tensile fracture of carbon nanotubes based on the numerical homogenization. Acta Phys. Pol. A 2017, 131, 440–442. [Google Scholar]
- Reddy, J.N. A simple higher-order theory for laminated composite plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, Sh.; Fadaee, M.; Es’haghi, M. A novel approach for in-plane/out-of-plane frequency analysis of functionally graded circular/annular plates. Int. J. Mech. Sci. 2010, 52, 1025–1035. [Google Scholar] [CrossRef]
- Muc, A.; Kędziora, P.; Stawiarski, A. Buckling enhancement of laminated composite structures partially covered by piezoelectric actuators. Eur. J. Mech. A 2019, 73, 112–125. [Google Scholar] [CrossRef]
- Muc, A.; Chwał, M.; Barski, M. Remarks on experimental and theoretical investigations of buckling loads for laminated plated and shell structures. Compos. Struct. 2018, 203, 861–874. [Google Scholar] [CrossRef]
- Shi, J.-X.; Natsuki, T.; Lei, X.-W.; Ni, Q.-Q. Equivalent Young’s modulus and thickness of graphene sheets for the continuum mechanical models. Appl. Phys. Lett. 2014, 104, 223101. [Google Scholar] [CrossRef]
- Shi, J.-X.; Ni, Q.-Q.; Lei, X.-W.; Natsuki, T. Study on wave propagation characteristics of double-layer graphene sheets via nonlocal Mindlin-Reissner plate theory. Int. J. Mech. Sci. 2014, 84, 25–30. [Google Scholar] [CrossRef]
- Shi, J.-X.; Ni, Q.-Q.; Lei, X.-W.; Natsuki, T. Nonlocal vibration analysis of nanomechanical systems resonators using circular double-layer graphene sheets. Appl. Phys. A 2014, 115, 213–219. [Google Scholar] [CrossRef]
- Muc, A. Choice of design variables in the stacking sequence optimization for laminated structures. Mech. Compos. Mater. 2016, 52, 211–224. [Google Scholar] [CrossRef]
- Muc, A.; Chwał, M. Analytical discrete stacking sequence optimization of rectangular composite plates subjected to buckling and FPF constraints. J. Theor. Appl. Mech. 2016, 54, 423–436. [Google Scholar] [CrossRef]
- Muc, A. Transverse shear effects in stability problems of laminated shallow shells. Compos. Struct. 1989, 12, 171–180. [Google Scholar] [CrossRef]
- Shi, J.W.; Nakatani, A.; Kitagawa, H. Vibration analysis of fully clamped arbitrarily laminated plate. Compos. Struct. 2004, 63, 115–122. [Google Scholar] [CrossRef]
- Muc, A.; Barski, M. Design of particulate-reinforced composite materials. Materials 2018, 11, 234. [Google Scholar] [CrossRef]
- Barski, M.; Chwał, M.; Kędziora, P. Molecular dynamics in simulation of magneto-rheological fluids behavior. Key Eng. Mater. 2013, 542, 11–27. [Google Scholar] [CrossRef]





| Classical Plate Theory (CPT) | First Order Shear Deformation Theory (FSDT) | Higher Order Shear Deformation Theory (HSDT)–Reddy [67] | Higher Order Shear Deformation Theory (HSDT)–Hosseini-Hashemi et al. [68] | |
|---|---|---|---|---|
| F(z) | 0 | z; the second term in Equation (10) is eliminated |
| CPT | FSDT/HSDT | |
|---|---|---|
| Equations of equilibrium | ||
| Kinematical variables | u, v, w | u, v, w, ψ1, ψ2 |
| Stress resultants | , , , , , | , , , , , , , |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chwał, M.; Muc, A. Buckling and Free Vibrations of Nanoplates—Comparison of Nonlocal Strain and Stress Approaches. Appl. Sci. 2019, 9, 1409. https://doi.org/10.3390/app9071409
Chwał M, Muc A. Buckling and Free Vibrations of Nanoplates—Comparison of Nonlocal Strain and Stress Approaches. Applied Sciences. 2019; 9(7):1409. https://doi.org/10.3390/app9071409
Chicago/Turabian StyleChwał, Małgorzata, and Aleksander Muc. 2019. "Buckling and Free Vibrations of Nanoplates—Comparison of Nonlocal Strain and Stress Approaches" Applied Sciences 9, no. 7: 1409. https://doi.org/10.3390/app9071409
APA StyleChwał, M., & Muc, A. (2019). Buckling and Free Vibrations of Nanoplates—Comparison of Nonlocal Strain and Stress Approaches. Applied Sciences, 9(7), 1409. https://doi.org/10.3390/app9071409