Mathematical Modeling of the Effect of Water Splitting on Ion Transfer in the Depleted Diffusion Layer Near an Ion-Exchange Membrane
Abstract
:1. Introduction
2. Mathematical Description
2.1. Formulation of the Problem. Governing Equations and Additional Conditions
2.2. Transformation and Integration of the Equations. Relationships between the Fluxes
2.3. Approximate Solution. The Diffusion Layer Structure
2.3.1. Equations in Dimensionless Form
2.3.2. Thicknesses of Different Zones. Stitching of Solutions
2.3.3. Potential Drops
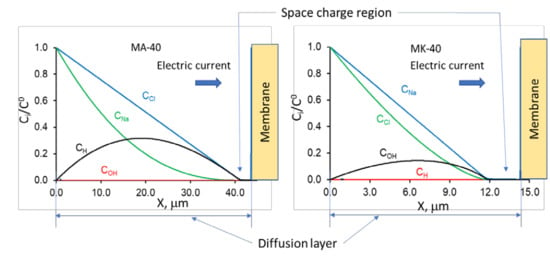
3. Experimental CVC Treatment
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Thickness of Different Zones of the Depleted Diffusion Layer
Appendix B. Space Charge and Relation between the Strengths of Electric Field in the Membrane and Solution
Appendix C. Potential Drops in Different Zones
Appendix C.1. Electroneutral Zone ()
Appendix C.2. Electromigration Space Charge Region ()
Appendix D. Concentration Profiles
Appendix D.1. Electroneutral Zone ()
Appendix D.2. Electromigration Space Charge Region ()
Appendix D.3. Equilibrium Electric Double Layer ()
References
- Valero, F.; Arbós, R. Desalination of brackish river water using Electrodialysis Reversal (EDR). Desalination 2010, 253, 170–174. [Google Scholar] [CrossRef]
- Burn, S.; Hoang, M.; Zarzo, D.; Olewniak, F.; Campos, E.; Bolto, B.; Barron, O. Desalination techniques — A review of the opportunities for desalination in agriculture. Desalination 2015, 364, 2–16. [Google Scholar] [CrossRef]
- Chehayeb, K.M.; Farhat, D.M.; Nayar, K.G.; Lienhard, J.H. Optimal design and operation of electrodialysis for brackish-water desalination and for high-salinity brine concentration. Desalination 2017, 420, 167–182. [Google Scholar] [CrossRef]
- Nayar, K.G.; Lienhard V, J.H. Brackish water desalination for greenhouse agriculture: Comparing the costs of RO, CCRO, EDR, and monovalent-selective EDR. Desalination 2020, 475, 114188. [Google Scholar] [CrossRef] [Green Version]
- Al-Amshawee, S.; Yunus, M.Y.B.M.; Azoddein, A.A.M.; Hassell, D.G.; Dakhil, I.H.; Hasan, H.A. Electrodialysis desalination for water and wastewater: A review. Chem. Eng. J. 2020, 380, 122231. [Google Scholar] [CrossRef]
- Campione, A.; Cipollina, A.; Toet, E.; Gurreri, L.; Bogle, I.D.L.; Micale, G. Water desalination by capacitive electrodialysis: Experiments and modelling. Desalination 2020, 473, 114150. [Google Scholar] [CrossRef]
- Turek, M.; Laskowska, E.; Mitko, K.; Chorążewska, M.; Dydo, P.; Piotrowski, K.; Jakóbik-Kolon, A. Application of nanofiltration and electrodialysis for improved performance of a salt production plant. Desalination Water Treat. 2017, 64, 244–250. [Google Scholar] [CrossRef]
- Chen, G.Q.; Eschbach, F.I.I.; Weeks, M.; Gras, S.L.; Kentish, S.E. Removal of lactic acid from acid whey using electrodialysis. Sep. Purif. Technol. 2016, 158, 230–237. [Google Scholar] [CrossRef]
- Merkel, A.; Ashrafi, A.M.; Ečer, J. Bipolar membrane electrodialysis assisted pH correction of milk whey. J. Membr. Sci. 2018, 555, 185–196. [Google Scholar] [CrossRef]
- Bazinet, L.; Firdaous, L. Recent patented applications of ion-exchange membranes in the agrifood sector. Recent Pat. Chem. Eng. 2011, 4, 207–216. [Google Scholar] [CrossRef]
- Taller, D.; Richards, K.; Slouka, Z.; Senapati, S.; Hill, R.; Go, D.B.; Chang, H.-C. On-chip surface acoustic wave lysis and ion-exchange nanomembrane detection of exosomal RNA for pancreatic cancer study and diagnosis. Lab Chip. 2015, 15, 1656–1666. [Google Scholar] [CrossRef] [PubMed]
- La Cerva, M.; Gurreri, L.; Cipollina, A.; Tamburini, A.; Ciofalo, M.; Micale, G. Modelling and cost analysis of hybrid systems for seawater desalination: Electromembrane pre-treatments for Reverse Osmosis. Desalination 2019, 467, 175–195. [Google Scholar] [CrossRef]
- Kadel, S.; Pellerin, G.; Thibodeau, J.; Perreault, V.; Lainé, C.; Bazinet, L. How molecular weight cut-offs and physicochemical properties of polyether sulfone membranes affect peptide migration and selectivity during electrodialysis with filtration membranes. Membranes 2019, 9, 153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deng, D.; Dydek, E.V.; Han, J.-H.; Schlumpberger, S.; Mani, A.; Zaltzman, B.; Bazant, M.Z. Overlimiting current and shock electrodialysis in porous media. Langmuir 2013, 29, 16167–16177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alkhadra, M.A.; Gao, T.; Conforti, K.M.; Tian, H.; Bazant, M.Z. Small-scale desalination of seawater by shock electrodialysis. Desalination 2020, 476, 114219. [Google Scholar] [CrossRef]
- Pan, S.-Y.; Snyder, S.W.; Ma, H.-W.; Lin, Y.J.; Chiang, P.-C. Development of a resin wafer electrodeionization process for impaired water desalination with high energy efficiency and productivity. ACS Sustain. Chem. Eng. 2017, 5, 2942–2948. [Google Scholar] [CrossRef]
- Park, S.; Kwak, R. Microscale electrodeionization: In situ concentration profiling and flow visualization. Water Res. 2020, 170, 115310. [Google Scholar] [CrossRef]
- de Jong, J.; Lammertink, R.G.H.; Wessling, M. Membranes and microfluidics: A review. Lab Chip. 2006, 6, 1125. [Google Scholar] [CrossRef]
- Kim, S.J.; Ko, S.H.; Kang, K.H.; Han, J. Direct seawater desalination by ion concentration polarization. Nat. Nanotechnol. 2010, 5, 297–301. [Google Scholar] [CrossRef]
- Slouka, Z.; Senapati, S.; Chang, H.-C. Microfluidic systems with ion-selective membranes. Annu. Rev. Anal. Chem. 2014, 7, 317–335. [Google Scholar] [CrossRef] [Green Version]
- Nikonenko, V.V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 342, 85–106. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 2000, 62, 2238–2251. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, I.; Zaltzman, B. Equilibrium electro-osmotic instability in concentration polarization at a perfectly charge-selective interface. Phys. Rev. Fluids 2017, 2, 093702. [Google Scholar] [CrossRef]
- Dukhin, S.S.; Mishchuk, N.A. Intensification of electrodialysis based on electroosmosis of the second kind. J. Membr. Sci. 1993, 79, 199–210. [Google Scholar] [CrossRef]
- de Valença, J.; Jõgi, M.; Wagterveld, R.M.; Karatay, E.; Wood, J.A.; Lammertink, R.G.H. Confined electroconvective vortices at structured ion exchange membranes. Langmuir 2018, 34, 2455–2463. [Google Scholar] [CrossRef] [Green Version]
- Roghmans, F.; Evdochenko, E.; Stockmeier, F.; Schneider, S.; Smailji, A.; Tiwari, R.; Mikosch, A.; Karatay, E.; Kühne, A.; Walther, A.; et al. 2D patterned ion-exchange membranes induce electroconvection. Adv. Mater. Interfaces 2019, 6, 1801309. [Google Scholar] [CrossRef] [Green Version]
- Simons, R. Water splitting in ion exchange membranes. Electrochim. Acta 1985, 30, 275–282. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Shel’deshov, N.V.; Gnusin, N.P. Dissociation of water molecules in systems with ion-exchange membranes. Russ. Chem. Rev. 1988, 57, 801–808. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Pismenskaya, N.D.; Belova, E.I.; Sistat, P.; Huguet, P.; Pourcelly, G.; Larchet, C. Intensive current transfer in membrane systems: Modelling, mechanisms and application in electrodialysis. Adv. Colloid Interface Sci. 2010, 160, 101–123. [Google Scholar] [CrossRef]
- Slouka, Z.; Senapati, S.; Yan, Y.; Chang, H.-C. Charge inversion, water splitting, and vortex suppression due to DNA sorption on ion-selective membranes and their ion-current signatures. Langmuir 2013, 29, 8275–8283. [Google Scholar] [CrossRef]
- Gnusin, N.P.; Zabolotskii, V.I.; Nikonenko, V.V.; Urtenov, M.K. Convective-diffusion model of electrodialytic desalination-limiting current and diffusion layer. Sov. Electrochem. 1986, 22, 273–278. [Google Scholar]
- Mishchuk, N.; Gonzalez-Caballero, F.; Takhistov, P. Electroosmosis of the second kind and current through curved interface. Colloids Surf. A Physicochem. Eng. Asp. 2001, 181, 131–144. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Equilibrium electroconvective instability. Phys. Rev. Lett. 2015, 114, 114502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaltzman, B.; Rubinstein, I. Electro-osmotic slip and electroconvective instability. J. Fluid Mech. 2007, 579, 173–226. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Mareev, S.A.; Pis’menskaya, N.D.; Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Pourcelly, G. Effect of electroconvection and its use in intensifying the mass transfer in electrodialysis (Review). Russ J Electrochem 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Kwak, R.; Guan, G.; Peng, W.K.; Han, J. Microscale electrodialysis: Concentration profiling and vortex visualization. Desalination 2013, 308, 138–146. [Google Scholar] [CrossRef]
- Shelistov, V.S.; Demekhin, E.A.; Ganchenko, G.S. Electrokinetic instability near charge-selective hydrophobic surfaces. Phys. Rev. E 2014, 90, 013001. [Google Scholar] [CrossRef] [Green Version]
- Karatay, E.; Druzgalski, C.L.; Mani, A. Simulation of chaotic electrokinetic transport: Performance of commercial software versus custom-built direct numerical simulation codes. J. Colloid Interface Sci. 2015, 446, 67–76. [Google Scholar] [CrossRef]
- Davidson, S.M.; Wessling, M.; Mani, A. On the dynamical regimes of pattern-accelerated electroconvection. Sci. Rep. 2016, 6, 22505. [Google Scholar] [CrossRef]
- Chang, H.-C.; Yossifon, G.; Demekhin, E.A. Nanoscale electrokinetics and microvortices: How microhydrodynamics affects nanofluidic ion flux. Annu. Rev. Fluid Mech. 2012, 44, 401–426. [Google Scholar] [CrossRef] [Green Version]
- Nikonenko, V.V.; Vasil’eva, V.I.; Akberova, E.M.; Uzdenova, A.M.; Urtenov, M.K.; Kovalenko, A.V.; Pismenskaya, N.P.; Mareev, S.A.; Pourcelly, G. Competition between diffusion and electroconvection at an ion-selective surface in intensive current regimes. J. Colloid Interface Sci. 2016, 235, 233–246. [Google Scholar] [CrossRef] [PubMed]
- Zabolotsky, V.I.; Korzhov, A.N.; But, A.Y.; Melnikov, S.S. Reagent-free electromembrane process for decarbonization of natural water. Membr. Membr. Technol. 2019, 1, 341–346. [Google Scholar] [CrossRef] [Green Version]
- Mikhaylin, S.; Bazinet, L. Fouling on ion-exchange membranes: Classification, characterization and strategies of prevention and control. Adv. Colloid Interf. Sci. 2016, 229, 34–56. [Google Scholar] [CrossRef] [PubMed]
- Dufton, G.; Mikhaylin, S.; Gaaloul, S.; Bazinet, L. Positive impact of pulsed electric field on lactic acid removal, demineralization and membrane scaling during acid whey electrodialysis. Int. J. Mol. Sci. 2019, 20, 797. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lemay, N.; Mikhaylin, S.; Bazinet, L. Voltage spike and electroconvective vortices generation during electrodialysis under pulsed electric field: Impact on demineralization process efficiency and energy consumption. Innov. Food Sci. Emerg. Technol. 2019, 52, 221–231. [Google Scholar] [CrossRef]
- Andreeva, M.A.; Gil, V.V.; Pismenskaya, N.D.; Dammak, L.; Kononenko, N.A.; Larchet, C.; Grande, D.; Nikonenko, V.V. Mitigation of membrane scaling in electrodialysis by electroconvection enhancement, pH adjustment and pulsed electric field application. J. Membr. Sci. 2018, 549, 129–140. [Google Scholar] [CrossRef]
- Simons, R. Strong electric field effects on proton transfer between membrane-bound amines and water. Nature 1979, 280, 824–826. [Google Scholar] [CrossRef]
- Simons, R. Electric field effects on proton transfer between ionizable groups and water in ion exchange membranes. Electrochim. Acta 1984, 29, 151–158. [Google Scholar] [CrossRef]
- Timashev, S.F.; Kirganova, E.V. Mechanism of the electrolytic decomposition of water-molecules in bipolar ion-exchange membranes. Sov. Electrochem. 1981, 17, 366–369. [Google Scholar]
- Mafé, S.; Ramírez, P.; Alcaraz, A. Electric field-assisted proton transfer and water dissociation at the junction of a fixed-charge bipolar membrane. Chem. Phys. Lett. 1998, 294, 406–412. [Google Scholar] [CrossRef]
- Strathmann, H.; Krol, J.J.; Rapp, H.-J.; Eigenberger, G. Limiting current density and water dissociation in bipolar membranes. J. Membr. Sci. 1997, 125, 123–142. [Google Scholar] [CrossRef] [Green Version]
- Umnov, V.V.; Shel’deshov, N.V.; Zabolotskii, V.I. Current-voltage curve for the space charge region of a bipolar membrane. Russ. J. Electrochem. 1999, 35, 871–878. [Google Scholar]
- Abdu, S.; Martí-Calatayud, M.-C.; Wong, J.E.; García-Gabaldón, M.; Wessling, M. Layer-by-layer modification of cation exchange membranes controls ion selectivity and water splitting. ACS Appl. Mater. Interfaces 2014, 6, 1843–1854. [Google Scholar] [CrossRef] [PubMed]
- Femmer, R.; Mani, A.; Wessling, M. Ion transport through electrolyte/polyelectrolyte multi-layers. Sci. Rep. 2015, 5, 11583. [Google Scholar] [CrossRef] [Green Version]
- Martí-Calatayud, M.C.; Evdochenko, E.; Bär, J.; García-Gabaldón, M.; Wessling, M.; Pérez-Herranz, V. Tracking homogeneous reactions during electrodialysis of organic acids via EIS. J. Membr. Sci. 2020, 595, 117592. [Google Scholar] [CrossRef]
- Urtenov, M.K.; Pismensky, A.V.; Nikonenko, V.V.; Kovalenko, A.V. Mathematical modeling of ion transport and water dissociation at the ion-exchange membrane/solution interface in intense current regimes. Pet. Chem. 2018, 58, 121–129. [Google Scholar] [CrossRef]
- Kharkats, Y.I. The mechanism of “‘supralimiting’” currents at ion-exchange membrane/electrolyte interfaces. Soviet Electrochemistry 1985, 21, 917–920. [Google Scholar]
- Kharkats, Y.I.; Sokirko, A.V. Theory of the effect of migration current exaltation taking into account dissociation-recombination reactions. J. Electroanal. Chem. Interf. Electrochem. 1991, 303, 27–44. [Google Scholar] [CrossRef]
- Zholkovskij, E.K. The over-limiting current in the system: Ion-exchange membrane/electrolyte solution. Elektrokhimiya 1987, 23, 180. [Google Scholar]
- Gnusin, N.P. Overlimiting electrodiffusion transport in the diffusion layer as a function of rate constants of dissociation and recombination of water: A numerical calculation. Russ. J. Electrochem. 2002, 38, 839–845. [Google Scholar] [CrossRef]
- Volgin, V.M.; Davydov, A.D. Ionic transport through ion-exchange and bipolar membranes. J. Membr. Sci. 2005, 259, 110–121. [Google Scholar] [CrossRef]
- Stodollick, J.; Femmer, R.; Gloede, M.; Melin, T.; Wessling, M. Electrodialysis of itaconic acid: A short-cut model quantifying the electrical resistance in the overlimiting current density region. J. Membr. Sci. 2014, 453, 275–281. [Google Scholar] [CrossRef]
- Listovnichy, A.V. Passage of currents higher than the limiting one through the electrode–electrolyte solution system. Sov. Electrochem. 1989, 25, 1651–1658. [Google Scholar]
- Nikonenko, V.V.; Zabolotskii, V.I.; Gnusin, N.P. Electric transport of ions through diffusion layers with impaired electroneutrality. Sov. Electrochem. 1989, 25, 262–266. [Google Scholar]
- Babeshko, V.A.; Zabolotskii, V.I.; Korzhenko, N.M.; Seidov, R.R.; Urtenov, M.K. The theory of the steady-state transfer of binary electrolytes in a unidimensional case. Russ. J. Electrochem. 1997, 33, 793–800. [Google Scholar]
- Chu, K.T.; Bazant, M.Z. Electrochemical thin films at and above the classical limiting current. SIAM J. Appl. Math. 2005, 65, 1485–1505. [Google Scholar] [CrossRef] [Green Version]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric effects in the dynamics of electrolytes at large applied voltages. I. Double-layer charging. Phys. Rev. E 2007, 75, 021502. [Google Scholar] [CrossRef] [Green Version]
- Urtenov, M.A.-K.; Kirillova, E.V.; Seidova, N.M.; Nikonenko, V.V. Decoupling of the Nernst−Planck and Poisson equations. application to a membrane system at overlimiting currents. J. Phys. Chem. B 2007, 111, 14208–14222. [Google Scholar] [CrossRef]
- Smyrl, W.H.; Newman, J. Double layer structure at the limiting current. Trans. Faraday Soc. 1967, 63, 207. [Google Scholar] [CrossRef] [Green Version]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 1979, 75, 231. [Google Scholar] [CrossRef]
- Manzanares, J.A.; Murphy, W.D.; Mafe, S.; Reiss, H. Numerical simulation of the nonequilibrium diffuse double layer in ion-exchange membranes. J. Phys. Chem. 1993, 97, 8524–8530. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V.; Pismenskaya, N.D.; Laktionov, E.V.; Urtenov, M.K.; Strathmann, H.; Wessling, M.; Koops, G.H. Coupled transport phenomena in overlimiting current electrodialysis. Sep. Purif. Technol. 1998, 14, 255–267. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V.; Pismenskaya, N.D. On the role of gravitational convection in the transfer enhancement of salt ions in the course of dilute solution electrodialysis. J. Membr. Sci. 1996, 119, 171–181. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Concentration polarization of interface and non-linear electrokinetic phenomena. J. Colloid Interf. Sci. 2010, 160, 16–39. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B.; Kedem, O. Electric fields in and around ion-exchange membranes. J. Membr. Sci. 1997, 125, 17–21. [Google Scholar] [CrossRef]
- Simons, R.; Khanarian, G. Water dissociation in bipolar membranes: Experiments and theory. J. Membrain Biol. 1978, 38, 11–30. [Google Scholar] [CrossRef]
- Grafov, B.M.; Chernenko, A.A. The theory of the passage of a direct current through a binary electrolyte solution. Dokl. Akad. Nauk SSSR. 1962, 146, 135–138, (in Rus.). [Google Scholar]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikonenko, V.; Urtenov, M.; Mareev, S.; Pourcelly, G. Mathematical Modeling of the Effect of Water Splitting on Ion Transfer in the Depleted Diffusion Layer Near an Ion-Exchange Membrane. Membranes 2020, 10, 22. https://doi.org/10.3390/membranes10020022
Nikonenko V, Urtenov M, Mareev S, Pourcelly G. Mathematical Modeling of the Effect of Water Splitting on Ion Transfer in the Depleted Diffusion Layer Near an Ion-Exchange Membrane. Membranes. 2020; 10(2):22. https://doi.org/10.3390/membranes10020022
Chicago/Turabian StyleNikonenko, Victor, Mahamet Urtenov, Semyon Mareev, and Gérald Pourcelly. 2020. "Mathematical Modeling of the Effect of Water Splitting on Ion Transfer in the Depleted Diffusion Layer Near an Ion-Exchange Membrane" Membranes 10, no. 2: 22. https://doi.org/10.3390/membranes10020022
APA StyleNikonenko, V., Urtenov, M., Mareev, S., & Pourcelly, G. (2020). Mathematical Modeling of the Effect of Water Splitting on Ion Transfer in the Depleted Diffusion Layer Near an Ion-Exchange Membrane. Membranes, 10(2), 22. https://doi.org/10.3390/membranes10020022