Optimising the Flux Enhancer Dosing Strategy in a Pilot-Scale Anaerobic Membrane Bioreactor by Mathematical Modelling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Data
2.2. General Model Description and Approach
2.3. Biochemical-Flocculation Model
2.4. AnMBR Filtration: Alternate FR_RIS Models
2.4.1. Resistance-In-Series (RIS) Submodel
2.4.2. Alternate Specific Cake Resistance (SCR) Submodels
2.4.3. Alternate Deposition Submodels
2.5. AnMBR Filtration: Alternate Empirical FR Models
2.6. AnDFCm Filtration: Alternate Models
- The gas superficial velocity in the AnMBR membrane tank () was replaced by the crossflow velocity in the AnDFCm membrane tube ( = 1.5 m s−1);
- The transmembrane flux was = (1.67 × 10−5 m3 m−2 s−1) and = ;
- There were no relaxation cycles (continuous filtration);
- The parameters of the mixed liquor viscosity model, and in Equation (36), were estimated based on the viscosity measurement performed in the AnDFCm installation with sludge samples with different TSS, presented in Section S2;
- Deposition Submodels D1a and D1b were not used because they were equal to D1c for the AnDFCm installations; the superficial velocity in the AnDFCm installation ( = 1.5 m s−1) was three orders of magnitude higher than in the AnMBR (0.5 × 10−3 < < 5.7 × 10−3 m s−1), and thus in Equations (31) and (32).
2.7. Model Implementation and Parameter Values
2.8. Model Calibration and Validation
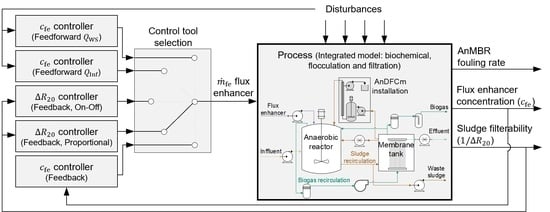
2.9. Control Tools for Flux Enhancer Dosage
3. Results and Discussion
3.1. Biochemical-Flocculation Model
3.2. AnMBR Filtration Model
3.3. AnDFCm Filtration Model
3.4. Model Limitation, Applicability, and Further Development
3.5. Control Tools for Dosing Flux Enhancer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- van Lier, J.B.; Mahmoud, N.; Zeeman, G. Anaerobic Wastewater Treatment. In Biological Wastewater Treatment, Principles, Modelling and Design, 2nd ed.; van Loosdrecht, M.C.M., Ekama, G.A., Brdjanovic, D., Eds.; IWA Publishing: London, UK, 2020; ISBN 9781789060355. [Google Scholar]
- Shin, C.; Bae, J. Current status of the pilot-scale anaerobic membrane bioreactor treatments of domestic wastewaters: A critical review. Bioresour. Technol. 2018, 247, 1038–1046. [Google Scholar] [CrossRef]
- Robles, A.; Ruano, M.V.; Charfi, A.; Lesage, G.; Heran, M.; Harmand, J.; Seco, A.; Steyer, J.-P.; Batstone, D.J.; Kim, J.; et al. A review on anaerobic membrane bioreactors (AnMBRs) focused on modelling and control aspects. Bioresour. Technol. 2018, 270, 612–626. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoon, S.; Collins, J.H. A novel flux enhancing method for membrane bioreactor (MBR) process using polymer. Desalination 2006, 191, 52–61. [Google Scholar] [CrossRef]
- Iversen, V.; Mehrez, R.; Horng, R.Y.; Chen, C.H.; Meng, F.; Drews, A.; Lesjean, B.; Ernst, M.; Jekel, M.; Kraume, M. Fouling mitigation through flocculants and adsorbents addition in membrane bioreactors: Comparing lab and pilot studies. J. Memb. Sci. 2009, 345, 21–30. [Google Scholar] [CrossRef]
- Díaz, H.; Azócar, L.; Torres, A.; Lopes, S.I.C.; Jeison, D. Use of flocculants for increasing permeate flux in anaerobic membrane bioreactors. Water Sci. Technol. 2014, 69, 2237–2242. [Google Scholar] [CrossRef]
- Kooijman, G.; Lopes, W.; Zhou, Z.; Guo, H.; de Kreuk, M.; Spanjers, H.; van Lier, J. Impact of coagulant and flocculant addition to an anaerobic dynamic membrane bioreactor (AnDMBR) treating waste-activated sludge. Membranes 2017, 7, 18. [Google Scholar] [CrossRef] [Green Version]
- Braguglia, C.M.; Mininni, G.; Rolle, E. Influence of anaerobic digestion on particle surface charge and optimal polymer dosage. Water Sci. Technol. 2006, 54, 43–50. [Google Scholar] [CrossRef]
- Gkotsis, P.; Peleka, E.; Zamboulis, D.; Mitrakas, M.; Tolkou, A.; Zouboulis, A. Wastewater Treatment in Membrane Bioreactors: The Use of Polyelectrolytes to Control Membrane Fouling. Environ. Process. 2017, 4, 9–21. [Google Scholar] [CrossRef]
- Wozniak, T. MBR design and operation using MPE-technology (Membrane Performance Enhancer). Desalination 2010, 250, 723–728. [Google Scholar] [CrossRef]
- Collins, J.H.; Yoon, S.-H.; Musale, D.; Kong, J.F.; Koppes, J.; Sundararajan, S.; Tsai, S.-P.; Hallsby, G.A.; Cachia, P.; Kronoveter, K. Membrane performance enhancer evaluations on pilot- and full-scale membrane bioreactors. Water Environ. J. 2006, 20, 43–47. [Google Scholar] [CrossRef]
- Alkmim, A.R.; da Costa, P.R.; Moser, P.B.; França Neta, L.S.; Santiago, V.M.J.; Cerqueira, A.C.; Amaral, M.C.S. Long-term evaluation of different strategies of cationic polyelectrolyte dosage to control fouling in a membrane bioreactor treating refinery effluent. Environ. Technol. 2016, 37, 1026–1035. [Google Scholar] [CrossRef] [PubMed]
- Odriozola, M.; Morales, N.; Vázquez-Padín, J.R.; Lousada-Ferreira, M.; Spanjers, H.; van Lier, J.B. Fouling Mitigation by Cationic Polymer Addition into a Pilot-Scale Anaerobic Membrane Bioreactor Fed with Blackwater. Polymers 2020, 12, 2383. [Google Scholar] [CrossRef] [PubMed]
- Guo, W.S.; Vigneswaran, S.; Ngo, H.H.; Kandasamy, J.; Yoon, S. The role of a membrane performance enhancer in a membrane bioreactor: A comparison with other submerged membrane hybrid systems. Desalination 2008, 231, 305–313. [Google Scholar] [CrossRef] [Green Version]
- Hwang, B.K.; Lee, W.N.; Park, P.K.; Lee, C.H.; Chang, I.S. Effect of membrane fouling reducer on cake structure and membrane permeability in membrane bioreactor. J. Memb. Sci. 2007, 288, 149–156. [Google Scholar] [CrossRef]
- Jamal Khan, S.; Visvanathan, C.; Jegatheesan, V. Effect of powdered activated carbon (PAC) and cationic polymer on biofouling mitigation in hybrid MBRs. Bioresour. Technol. 2012, 113, 165–168. [Google Scholar] [CrossRef]
- Lee, W.N.; Chang, I.S.; Hwang, B.K.; Park, P.K.; Lee, C.H.; Huang, X. Changes in biofilm architecture with addition of membrane fouling reducer in a membrane bioreactor. Process Biochem. 2007, 42, 655–661. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Li, Y.; Hu, C. Influence of Filtration Aids on Continuous Filtration in Membrane Bioreactors. Ind. Eng. Chem. Res. 2014, 53, 7202–7208. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, Z.; Zhang, L.; Song, L. Performance enhancement and fouling mitigation by organic flocculant addition in membrane bioreactor at high salt shock. Bioresour. Technol. 2014, 164, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.-H.; Wu, C.-H.; Cheng, G.-F.; Hong, Q.-K.; Li, Y.-Z.; Wang, H.-Y. Impact of poly dimethyldiallylammonium chloride on membrane fouling mitigation in a membrane bioreactor. Environ. Technol. 2019, 40, 1043–1049. [Google Scholar] [CrossRef] [PubMed]
- Iversen, V. Comprehensive Assessment of Flux Enhancers in Membrane Bioreactors for Wastewater Treatment; Doctoral Thesis, Technische Universität: Berlin, Germany, 2010. [Google Scholar]
- Brauns, E.; Van Hoof, E.; Huyskens, C.; De Wever, H. On the concept of a supervisory, fuzzy set logic based, advanced filtration control in membrane bioreactors. Desalin. Water Treat. 2011, 29, 119–127. [Google Scholar] [CrossRef]
- Kraume, M.; Wedi, D.; Schaller, J.; Iversen, V.; Drews, A. Fouling in MBR: What use are lab investigations for full scale operation? Desalination 2009, 236, 94–103. [Google Scholar] [CrossRef]
- Naessens, W.; Maere, T.; Nopens, I. Critical review of membrane bioreactor models—Part 1: Biokinetic and filtration models. Bioresour. Technol. 2012, 122, 95–106. [Google Scholar] [CrossRef] [PubMed]
- Naessens, W.; Maere, T.; Ratkovich, N.; Vedantam, S.; Nopens, I. Critical review of membrane bioreactor models—Part 2: Hydrodynamic and integrated models. Bioresour. Technol. 2012, 122, 107–118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Odriozola, M.; Lousada-Ferreira, M.; Spanjers, H.; van Lier, J.B. Effect of sludge characteristics on optimal required dosage of flux enhancer in anaerobic membrane bioreactors. J. Memb. Sci. 2021, 619, 118776. [Google Scholar] [CrossRef]
- Christensen, M.L.; Niessen, W.; Sørensen, N.B.; Hansen, S.H.; Jørgensen, M.K.; Nielsen, P.H. Sludge fractionation as a method to study and predict fouling in MBR systems. Sep. Purif. Technol. 2018, 194, 329–337. [Google Scholar] [CrossRef]
- Judd, S.; Judd, C. The MBR Book: Principles and Applications of Membrane Bioreactors for Water and Wastewater Treatment, 2nd ed.; Judd, S., Judd, C., Eds.; Butterworth-Heinemann: Oxford, UK, 2011; ISBN 9780080966823. [Google Scholar]
- Remy, M.J.J. Low Concentration of Powdered Activated Carbon Decreases Fouling in Membrane Bioreactors. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 2012. [Google Scholar]
- Gil, J.A.; Krzeminski, P.; Van Lier, J.B.; Van Der Graaf, J.H.J.M.; Wijffels, T.; Prats, D. Analysis of the filterability in industrial MBRs. Influence of activated sludge parameters and constituents on filterability. J. Memb. Sci. 2011, 385–386, 96–109. [Google Scholar] [CrossRef]
- Huang, B.C.; Guan, Y.F.; Chen, W.; Yu, H.Q. Membrane fouling characteristics and mitigation in a coagulation-assisted microfiltration process for municipal wastewater pretreatment. Water Res. 2017, 123, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.; Evans, P.J.; Utter, J.; Malki, M.; Parameswaran, P. Dynamic monitoring and proactive fouling management in a pilot scale gas-sparged anaerobic membrane bioreactor. Environ. Sci. Water Res. Technol. 2020, 6, 2914–2925. [Google Scholar] [CrossRef]
- Hamedi, H.; Ehteshami, M.; Mirbagheri, S.A.; Rasouli, S.A.; Zendehboudi, S. Current Status and Future Prospects of Membrane Bioreactors (MBRs) and Fouling Phenomena: A Systematic Review. Can. J. Chem. Eng. 2019, 97, 32–58. [Google Scholar] [CrossRef] [Green Version]
- Belfort, G.; Davis, R.H.; Zydney, A.L. The behavior of suspensions and macromolecular solutions in crossflow microfiltration. J. Memb. Sci. 1994, 96, 1–58. [Google Scholar] [CrossRef]
- Shen, L.G.; Lei, Q.; Chen, J.R.; Hong, H.C.; He, Y.M.; Lin, H.J. Membrane fouling in a submerged membrane bioreactor: Impacts of floc size. Chem. Eng. J. 2015, 269, 328–334. [Google Scholar] [CrossRef]
- Lousada-Ferreira, M.; van Lier, J.B.; van der Graaf, J.H.J.M. Impact of suspended solids concentration on sludge filterability in full-scale membrane bioreactors. J. Memb. Sci. 2015, 476, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Batstone, D.J.; Keller, J.; Angelidaki, I.; Kalyuzhnyi, S.V.; Pavlostathis, S.G.; Rozzi, A.; Sanders, W.T.; Siegrist, H.; Vavilin, V.A. Anaerobic Digestion Model No. 1 (ADM1); IWA Publishing: London, UK, 2002; ISBN 1900222787/9781900222785. [Google Scholar]
- Batstone, D.J.; Puyol, D.; Flores-Alsina, X.; Rodríguez, J. Mathematical modelling of anaerobic digestion processes: Applications and future needs. Rev. Environ. Sci. Bio/Technol. 2015, 14, 595–613. [Google Scholar] [CrossRef]
- Donoso-Bravo, A.; Mailier, J.; Martin, C.; Rodríguez, J.; Aceves-Lara, C.A.; Wouwer, A. Vande Model selection, identification and validation in anaerobic digestion: A review. Water Res. 2011, 45, 5347–5364. [Google Scholar] [CrossRef] [PubMed]
- Barat, R.; Serralta, J.; Ruano, M.V.; Jiménez, E.; Ribes, J.; Seco, A.; Ferrer, J. Biological nutrient removal model no. 2 (BNRM2): A general model for wastewater treatment plants. Water Sci. Technol. 2013, 67, 1481–1489. [Google Scholar] [CrossRef] [Green Version]
- Benyahia, B.; Sari, T.; Cherki, B.; Harmand, J. Anaerobic membrane bioreactor modeling in the presence of Soluble Microbial Products (SMP)—The Anaerobic Model AM2b. Chem. Eng. J. 2013, 228, 1011–1022. [Google Scholar] [CrossRef] [Green Version]
- Odriozola, M.; Abraham, E.; Lousada-Ferreira, M.; Spanjers, H.; van Lier, J.B. Identification of the Methanogenesis Inhibition Mechanism Using Comparative Analysis of Mathematical Models. Front. Bioeng. Biotechnol. 2019, 7, 93. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; He, C.; Zhang, Y. Modeling membrane fouling in a submerged membrane bioreactor by considering the role of solid, colloidal and soluble components. J. Memb. Sci. 2012, 397–398, 102–111. [Google Scholar] [CrossRef]
- Cho, J.; Song, K.G.; Ahn, K.H. The activated sludge and microbial substances influences on membrane fouling in submerged membrane bioreactor: Unstirred batch cell test. Desalination 2005, 183, 425–429. [Google Scholar] [CrossRef]
- Zarragoitia-González, A.; Schetrite, S.; Alliet, M.; Jáuregui-Haza, U.; Albasi, C. Modelling of submerged membrane bioreactor: Conceptual study about link between activated slugde biokinetics, aeration and fouling process. J. Memb. Sci. 2008, 325, 612–624. [Google Scholar] [CrossRef] [Green Version]
- Charfi, A.; Thongmak, N.; Benyahia, B.; Aslam, M.; Harmand, J.; Amar, N.B.; Lesage, G.; Sridang, P.; Kim, J.; Heran, M. A modelling approach to study the fouling of an anaerobic membrane bioreactor for industrial wastewater treatment. Bioresour. Technol. 2017, 245, 207–215. [Google Scholar] [CrossRef]
- Zuthi, M.F.R.; Ngo, H.H.; Guo, W.S.; Li, J.X.; Xia, S.Q.; Zhang, Z.Q. New proposed conceptual mathematical models for biomass viability and membrane fouling of membrane bioreactor. Bioresour. Technol. 2013, 142, 737–740. [Google Scholar] [CrossRef] [PubMed]
- Jeldres, R.I.; Fawell, P.D.; Florio, B.J. Population balance modelling to describe the particle aggregation process: A review. Powder Technol. 2018, 326, 190–207. [Google Scholar] [CrossRef]
- Moreau, A.A.; Ratkovich, N.; Nopens, I.; van der Graaf, J.H.J.M. The (in)significance of apparent viscosity in full-scale municipal membrane bioreactors. J. Memb. Sci. 2009, 340, 249–256. [Google Scholar] [CrossRef]
- Geilvoet, S. The Delft Filtration Characterisation Method Assessing Membrane Bioreactor Activated Sludge Filterability; Delft University of Technology: Delft, The Netherlands, 2010. [Google Scholar]
- El-Naas, M.H.; Alhaija, M.A. Modelling of adsorption processes. In Mathematical Modelling; Brennan, C.R., Ed.; Nova Publishers, Inc.: New York, NY, USA, 2011; ISBN 9781612096513. [Google Scholar]
- Tugtas, A.E.; Tezel, U.; Pavlostathis, S.G. An extension of the Anaerobic Digestion Model No. 1 to include the effect of nitrate reduction processes. Water Sci. Technol. 2006, 54, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Astals, S.; Peces, M.; Batstone, D.J.; Jensen, P.D.; Tait, S. Characterising and modelling free ammonia and ammonium inhibition in anaerobic systems. Water Res. 2018, 143, 127–135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Janssen, L.P.B.; Warmoeskerken, M.M.C. Transport Phenomena Data Companion, 3rd ed.; Delftse Universitaire Pers: Delft, The Netherlands, 1997; ISBN 9040713022/9789040713026. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Chem. Eng. Res. Des. 1997, 75, S32–S48. [Google Scholar] [CrossRef]
- Naessens, W. Towards Improved Membrane Fouling Modelling: From an Empirical to a Spatially Explicit Framework. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2018. [Google Scholar]
- Jørgensen, M.K.; Keiding, K.; Christensen, M.L. On the reversibility of cake buildup and compression in a membrane bioreactor. J. Memb. Sci. 2014, 455, 152–161. [Google Scholar] [CrossRef]
- Robles, A.; Ruano, M.V.; Ribes, J.; Seco, A.; Ferrer, J. A filtration model applied to submerged anaerobic MBRs (SAnMBRs). J. Memb. Sci. 2013, 444, 139–147. [Google Scholar] [CrossRef] [Green Version]
- Bugge, T.V.; Jørgensen, M.K.; Christensen, M.L.; Keiding, K. Modeling cake buildup under TMP-step filtration in a membrane bioreactor: Cake compressibility is significant. Water Res. 2012, 46, 4330–4338. [Google Scholar] [CrossRef]
- Sørensen, B.L.; Sørensen, P.B. Structure Compression in Cake Filtration. J. Environ. Eng. 1997, 123, 345–353. [Google Scholar] [CrossRef]
- Boyle-Gotla, A.; Jensen, P.D.; Yap, S.D.; Pidou, M.; Wang, Y.; Batstone, D.J. Dynamic multidimensional modelling of submerged membrane bioreactor fouling. J. Memb. Sci. 2014, 467, 153–161. [Google Scholar] [CrossRef] [Green Version]
- Suh, C.; Lee, S.; Cho, J. Investigation of the effects of membrane fouling control strategies with the integrated membrane bioreactor model. J. Memb. Sci. 2013, 429, 268–281. [Google Scholar] [CrossRef]
- Mannina, G.; Di Bella, G.; Viviani, G. An integrated model for biological and physical process simulation in membrane bioreactors (MBRs). J. Memb. Sci. 2011, 376, 56–69. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, X.M. Modelling of membrane fouling in a submerged membrane bioreactor. J. Memb. Sci. 2006, 278, 151–161. [Google Scholar] [CrossRef]
- Nam, K.; Heo, S.; Rhee, G.; Kim, M.; Yoo, C. Dual-objective optimization for energy-saving and fouling mitigation in MBR plants using AI-based influent prediction and an integrated biological-physical model. J. Memb. Sci. 2021, 626, 119208. [Google Scholar] [CrossRef]
- Perry, R.H.; Green, D.W. Perry’s Chemical Engineers’ Handbook; McGraw-Hill Professional: Columbus, OH, USA, 2008; Volume 1, ISBN 9788578110796. [Google Scholar]
- Krauth, K.; Staab, K.F. Pressurized bioreactor with membrane filtration for wastewater treatment. Water Res. 1993, 27, 405–411. [Google Scholar] [CrossRef]
- Feng, Y. Calibration and Verification of a Mathematical Model for the Simulation of Blackwater/Biowaste Digestion. Master’s Thesis, Hamburg University of Technology, Hamburg, Germany, 2004. [Google Scholar]
- Gorini, D.; Choubert, J.-M.; le Pimpec, P.; Heduit, A. Concentrations and fate of sugars, proteins and lipids during domestic and agro-industrial aerobic treatment. Water Sci. Technol. 2011, 63, 1669–1677. [Google Scholar] [CrossRef]
- Hubbe, M.A.; Wu, N.; Rojas, O.J.; Park, S. Permeation of a cationic polyelectrolyte into mesoporous silica. Part 3. Using adsorption isotherms to elucidate streaming potential results. Colloids Surf. A Physicochem. Eng. Asp. 2011, 381, 1–6. [Google Scholar] [CrossRef]
- Zhao, X.; Ma, J.; Ma, H.; Gao, D.; Lv, X.; Zhang, J. Adsorptive removal of vinyl polymer tanning agents from aqueous solution using wastewater activated sludge. Desalin. Water Treat. 2016, 57, 11422–11432. [Google Scholar] [CrossRef]
- Horvath, A.E.; Lindström, T.; Laine, J. On the indirect polyelectrolyte titration of cellulosic fibers. Conditions for charge stoichiometry and comparison with ESCA. Langmuir 2006, 22, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Robles, A.; Ruano, M.V.; Ribes, J.; Seco, A.; Ferrer, J. Global sensitivity analysis of a filtration model for submerged anaerobic membrane bioreactors (AnMBR). Bioresour. Technol. 2014, 158, 365–373. [Google Scholar] [CrossRef] [PubMed]
- Lidholm, O.; Ossiansson, E. Modeling Anaerobic Digestion—Validation and Calibration of the Siegrist Model with Uncertainty and Sensitivity Analysis. Master’s Thesis, Lund University, Lund, Sweden, 2008. [Google Scholar]
- Mara, D.; Horan, N.; Hao, O.J. Handbook of Water and Wastewater Microbiology; Academic Press: London, UK, 2003; ISBN 9780124701007. [Google Scholar]
- Durán, F. Modelación Matemática del Tratamiento Anaerobio de Aguas Residuales Urbanas Incluyendo las Bacterias Sulfatorreductoras. Aplicación a un Biorreactor Anaerobio de Membranas; Universitat Politècnica de València: Valencia, Spain, 2013. [Google Scholar]
- Metcalf, L.; Eddy, H.P.; Tchobanoglous, G.; Burton, F.L.; Stensel, H.D. Wastewater Engineering: Treatment and Reuse, 4th ed.; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef] [Green Version]
- Batstone, D.J.; Keller, J.; Blackall, L.L. The influence of substrate kinetics on the microbial community structure in granular anaerobic biomass. Water Res. 2004, 38, 1390–1404. [Google Scholar] [CrossRef]
- Guo, H.; Oosterkamp, M.J.; Tonin, F.; Hendriks, A.; Nair, R.; van Lier, J.B.; de Kreuk, M. Reconsidering hydrolysis kinetics for anaerobic digestion of waste activated sludge applying cascade reactors with ultra-short residence times. Water Res. 2021, 202, 117398. [Google Scholar] [CrossRef]
- Elmitwalli, T.A.; van Leeuwen, M.; Kujawa-Roeleveld, K.; Sanders, W.; Zeeman, G. Anaerobic biodegradability and digestion in accumulation systems for concentrated black water and kitchen organic-wastes. Water Sci. Technol. 2006, 53, 167–175. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wendland, C. Anerobic Digestion of Blackwater and Kitchen Refuse; Technischen Universität Hamburg-Harburg: Hamburg, Germany, 2008. [Google Scholar]
- Benedetti, L.; Claeys, F.; Nopens, I.; Vanrolleghem, P.A. Assessing the convergence of LHS Monte Carlo simulations of wastewater treatment models. Water Sci. Technol. 2011, 63, 2219–2224. [Google Scholar] [CrossRef] [Green Version]
- Sin, G.; Gernaey, K. Data Handling and Parameter Estimation. In Experimental Methods in Wastewater Treatment; van Loosdrecht, M.C.M., Nielsen, P.H., Lopez-Vazquez, C.M., Brdjanovic, D., Eds.; IWA Publishing: London, UK, 2016; pp. 201–234. ISBN 9781780404752. [Google Scholar]
- Merkus, H.G. Particle Size Measurements: Fundamentals, Practice, Quality; Springer Science & Business Media B.V.: Berlin/Heidelberg, Germany, 2009; ISBN 978-1-4020-9015-8. [Google Scholar]
- Dong, Q.; Parker, W.; Dagnew, M. Impact of FeCl3; dosing on AnMBR treatment of municipal wastewater. Water Res. 2015, 80, 281–293. [Google Scholar] [CrossRef]
- Dong, Q.; Parker, W.; Dagnew, M. Dynamic characterization of a FeCl3-dosed anaerobic membrane bioreactor (AnMBR) treating municipal wastewater. Water Sci. Technol. 2018, 2017, 481–491. [Google Scholar] [CrossRef] [PubMed]
- Evenblij, H. Filtration Characteristics in Membrane Bioreactors; Delft University of Technology: Delft, The Netherlands, 2006. [Google Scholar]
- Lousada-Ferreira, M.; Krzeminski, P.; Geilvoet, S.; Moreau, A.; Gil, J.A.; Evenblij, H.; van Lier, J.B.; van der Graaf, J.H.J.M.; Van Lier, J.B.; Van Der Graaf, J.H.J.M. Filtration characterization method as tool to assess membrane bioreactor sludge filterability-the Delft experience. Membranes 2014, 4, 227–242. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| SCR Submodel | Equation | Effects Considered | ||
|---|---|---|---|---|
| Colloidal Material | Particle Size | Compression, TMP | ||
| X | X | |||
| X | X | X | ||
| X | ||||
| X | X | |||
| X | ||||
| X | X | |||
| X | X | |||
| Component
Process | Deposited Particulate | Deposited Colloidal | Particulate in Bulk Liquid | Colloidal in Bulk Liquid | Deposition Submodel 1 (D1) (Drag Forces) | Deposition Submodel 2 (D2) (Drag and Lift Forces) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | Attachment of particulate material | 1 | −1 | (23) | (24) | ||||
| 2 | Detachment of particulate material by biogas sparging | −1 | 1 | (25) | (26) | ||||
| 3 | Attachment of colloidal material | 1 | −1 | (27) | (28) | ||||
| 4 | Detachment of colloidal material by biogas sparging | −1 | 1 | (29) | (30) | ||||
| Deposition Submodel | Equation | |
|---|---|---|
| D1a | with | (31) |
| D1b | with | (32) |
| D1c | (33) | |
| FR Model | ||
|---|---|---|
| 1 | (32) | |
| 2 | (37) | |
| 3 | (38) | |
| 4 | (39) | |
| 5 | (40) | |
| 6 | (41) | |
| Reference | Type of Control | Measured Variable | Controlled Variable | Calculation |
|---|---|---|---|---|
| FB__10 | Feedback, proportional | 1.6 × 10−7 | ||
| FB__8–12 | Feedback, on-off | 5 × 10−6 | ||
| FB_ | Feedback, proportional | 1 × 10−3 | ||
| FF_ | Feedforward, pulse + proportional 1 | |||
| FF_ | Feedforward, proportional | |||
| No_FE | No control | NA | NA | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Odriozola, M.; van Lier, J.B.; Spanjers, H. Optimising the Flux Enhancer Dosing Strategy in a Pilot-Scale Anaerobic Membrane Bioreactor by Mathematical Modelling. Membranes 2022, 12, 151. https://doi.org/10.3390/membranes12020151
Odriozola M, van Lier JB, Spanjers H. Optimising the Flux Enhancer Dosing Strategy in a Pilot-Scale Anaerobic Membrane Bioreactor by Mathematical Modelling. Membranes. 2022; 12(2):151. https://doi.org/10.3390/membranes12020151
Chicago/Turabian StyleOdriozola, Magela, Jules B. van Lier, and Henri Spanjers. 2022. "Optimising the Flux Enhancer Dosing Strategy in a Pilot-Scale Anaerobic Membrane Bioreactor by Mathematical Modelling" Membranes 12, no. 2: 151. https://doi.org/10.3390/membranes12020151
APA StyleOdriozola, M., van Lier, J. B., & Spanjers, H. (2022). Optimising the Flux Enhancer Dosing Strategy in a Pilot-Scale Anaerobic Membrane Bioreactor by Mathematical Modelling. Membranes, 12(2), 151. https://doi.org/10.3390/membranes12020151