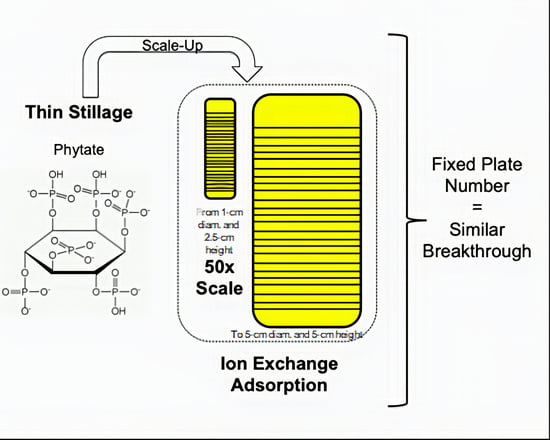
Volumetric Scale-Up of a Packed-Bed Ion-Exchange System to Extract Phytate from Thin Stillage
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental and Analytical Procedures
2.2. Model Development
3. Results and Discussion
3.1. Effect of the Column Height
3.2. The Effect of a Similar Q for Different Heights
3.3. Considerations Regarding the Scale-Up Approach for the Extraction of Phytate
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Maga, J.A. Phytate: Its chemistry, occurrence, food interactions, nutritional significance, and methods of analysis. J. Agric. Food Chem. 1982, 30, 1–9. [Google Scholar] [CrossRef]
- Cromwell, G.L.; Coffey, R.D.; Monegue, H.J.; Randolph, J.H. Efficacy of low-activity, microbial phytase in improving the bioavailability of phosphorus in corn-soybean meal diets for pigs. J. Anim. Sci. 1995, 73, 449–456. [Google Scholar] [CrossRef] [Green Version]
- Cai, K.; Shen, W.; Ren, B.; He, J.; Wu, S.; Wang, W. A phytic acid modified CoFe2O4 magnetic adsorbent with controllable morphology, excellent selective adsorption for dyes and ultra-strong adsorption ability for metal ions. Chem. Eng. J. 2017, 330, 936–946. [Google Scholar] [CrossRef]
- Li, P.; Wang, B.; Liu, Y.-Y.; Xu, Y.-J.; Jiang, Z.-M.; Dong, C.-H.; Zhang, L.; Liu, Y.; Zhu, P. Fully bio-based coating from chitosan and phytate for fire-safety and antibacterial cotton fabrics. Carbohydr. Polym. 2020, 237, 116173. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, Z.; Luo, K.; Xie, F.; He, Z.; Liao, H.; Giesy, J.P. The adsorption of phytate onto an Fe–Al–La trimetal composite adsorbent: Kinetics, isotherms, mechanism and implication. Environ. Sci.: Water Res. Technol. 2021, 7, 1971–1984. [Google Scholar] [CrossRef]
- Reis, C.E.R.; Rajendran, A.; Hu, B. New technologies in value addition to the thin stillage from corn-to-ethanol process. Rev. Environ. Sci. Bio/Technol. 2017, 16, 175–206. [Google Scholar] [CrossRef]
- He, Q.; Rodrigues Reis, C.E.; Wang, F.; Hu, B. Phytate extraction from coproducts of the dry-grind corn ethanol process. RSC Adv. 2017, 7, 5466–5472. [Google Scholar] [CrossRef] [Green Version]
- Reis, C.E.R.; He, Q.; Rajendran, A.; Hu, B. Retrofit Process Development for Phytate Extraction from Corn-Ethanol Coproducts Using Industrial Anion-Exchange Resins. Ind. Eng. Chem. Res. 2017, 56, 6391–6400. [Google Scholar] [CrossRef]
- Reis, C.E.R.; He, Q.; Urriola, P.E.; Shurson, G.C.; Hu, B. Effects of Modified Processes in Dry-Grind Ethanol Production on Phosphorus Distribution in Coproducts. Ind. Eng. Chem. Res. 2018, 57, 14861–14869. [Google Scholar] [CrossRef]
- Xu, Z.; Cai, J.-g.; Pan, B.-c. Mathematically modeling fixed-bed adsorption in aqueous systems. J. Zhejiang Univ. SCI. A 2013, 14, 155–176. [Google Scholar] [CrossRef] [Green Version]
- Greluk, M.; Hubicki, Z. Evaluation of polystyrene anion exchange resin for removal of reactive dyes from aqueous solutions. Chem. Eng. Res. Des. 2013, 91, 1343–1351. [Google Scholar] [CrossRef]
- Lorenz, A.J.; Scott, M.P.; Lamkey, K.R. Quantitative Determination of Phytate and Inorganic Phosphorus for Maize Breeding. Crop Sci. 2007, 47, 600–604. [Google Scholar] [CrossRef]
- Rajendran, A.; Fox, T.; Reis, C.R.; Wilson, B.; Hu, B. Deposition of manure nutrients in a novel mycoalgae biofilm for Nutrient management. Biocatal. Agric. Biotechnol. 2018, 14, 120–128. [Google Scholar] [CrossRef]
- Martin, A.J.; Synge, R.L.J.B.J. A new form of chromatogram employing two liquid phases: A theory of chromatography. 2. Application to the micro-determination of the higher monoamino-acids in proteins. Biochem. J. 1941, 35, 1358–1368. [Google Scholar] [CrossRef]
- Yamamoto, S.; Akazaki, N.; Kaltenbrunner, O.; Watler, P. Factors affecting dispersion in expanded bed chromatography. In Expanded Bed Chromatography; Mattiasson, B., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 1999; pp. 33–41. [Google Scholar]
- Hansen, E.B. Chromatographic Scale-Up on a Volume Basis. Preparative Chromatography for Separation of Proteins; Staby, A., Rathore, A.S., Ahuja, S., Eds.; Wiley Online Library: Hoboken, NJ, USA, 2017. [Google Scholar]
- van Deemter, J.J.; Zuiderweg, F.J.; Klinkenberg, A. Longitudinal diffusion and resistance to mass transfer as causes of nonideality in chromatography. Chem. Eng. Sci. 1995, 50, 3869–3882. [Google Scholar] [CrossRef]
- DeVault, D. The Theory of Chromatography. J. Am. Chem. Soc. 1943, 65, 532–540. [Google Scholar] [CrossRef]
- Ketelle, B.H.; Boyd, G.E. The Exchange Adsorption of Ions from Aqueous Solutions by Organic Zeolites. IV. The Separation of the Yttrium Group Rare Earths. J. Am. Chem. Soc. 1947, 69, 2800–2812. [Google Scholar] [CrossRef]
- Boyd, G.E. ION Exchange. Ann. Rev. Phys. Chem. 1951, 2, 309–342. [Google Scholar] [CrossRef]
- Glueckauf, E. Theory of chromatography. Part 10.—Formulæ for diffusion into spheres and their application to chromatography. Trans. Faraday Soc. 1955, 51, 1540–1551. [Google Scholar] [CrossRef]
- Watler, P.; Yamamoto, S.; Kaltenbrunner, O.; Feng, D.N. Engineering aspects of ion-exchange chromatography. In Scale-Up and Optimization in Preparative Chromatography; CRC Press: Boca Raton, FL, USA, 2002; pp. 132–176. [Google Scholar]
- Lapidus, L.; Amundson, N.R. Mathematics of Adsorption in Beds. VI. The Effect of Longitudinal Diffusion in Ion Exchange and Chromatographic Columns. J. Phys. Chem. 1952, 56, 984–988. [Google Scholar] [CrossRef]
- Colby, C.B.; O’Neill, B.K.; Middelberg, A.P.J. A Modified Version of the Volume-Averaged Continuum Theory To Predict Pressure Drop across Compressible Packed Beds of Sepharose Big-Beads SP. Biotechnol. Progr. 1996, 12, 92–99. [Google Scholar] [CrossRef]
- Soriano, G.A.; Titchener-Hooker, N.J.; Shamlou, P.A. The effects of processing scale on the pressure drop of compressible gel supports in liquid chromatographic columns. Bioproc. Eng. 1997, 17, 115–119. [Google Scholar] [CrossRef]
- Stickel, J.J.; Fotopoulos, A. Pressure-Flow Relationships for Packed Beds of Compressible Chromatography Media at Laboratory and Production Scale. Biotechnol. Prog. 2001, 17, 744–751. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, R.R.; Miller, J.E.; De Leon, P.; Leitch, W.E.; Cole, D.L.; Sanghvi, Y.S. Process Development for Purification of Therapeutic Antisense Oligonucleotides by Anion-Exchange Chromatography. Org. Proc. Res. Develop. 2000, 4, 205–213. [Google Scholar] [CrossRef]
- Heuer, C.; Hugo, P.; Mann, G.; Seidel-Morgenstern, A. Scale up in preparative chromatography. J. Chromat. A 1996, 752, 19–29. [Google Scholar] [CrossRef]
- Al-Jibbouri, S. Scale-up of chromatographic ion-exchange processes in biotechnology. J. Chromat. A 2006, 1116, 135–142. [Google Scholar] [CrossRef]
- Kalil, S.J.; Silveira, S.T.; Maugeri-Filho, F.; Rodrigues, M.I.J.B. Evaluation of different parameters for the purification of inulinase using an ion exchange fixed bed. Biotechnol. Bioproc. Eng. 2010, 15, 676–679. [Google Scholar] [CrossRef]
- Marcus, Y.; Howery, D.G. Ion Exchange Equilibrium Constants; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Bedzo, O.K.K.; Trollope, K.; Gottumukkala, L.D.; Coetzee, G.; Görgens, J.F. Amberlite IRA 900 versus calcium alginate in immobilization of a novel, engineered β-fructofuranosidase for short-chain fructooligosaccharide synthesis from sucrose. Biotechnol. Prog. 2019, 35, e2797. [Google Scholar] [CrossRef]


| Anion | qm (mg g−1) | R2 |
|---|---|---|
| Phytate-P | 130 | 0.9206 |
| NO3−-N | 36.28 | 0.9284 |
| Reactive PO43−-P | 68.98 | 0.9345 |
| SO42− | 47.35 | 0.9435 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues Reis, C.E.; Hu, B. Volumetric Scale-Up of a Packed-Bed Ion-Exchange System to Extract Phytate from Thin Stillage. Membranes 2022, 12, 230. https://doi.org/10.3390/membranes12020230
Rodrigues Reis CE, Hu B. Volumetric Scale-Up of a Packed-Bed Ion-Exchange System to Extract Phytate from Thin Stillage. Membranes. 2022; 12(2):230. https://doi.org/10.3390/membranes12020230
Chicago/Turabian StyleRodrigues Reis, Cristiano E., and Bo Hu. 2022. "Volumetric Scale-Up of a Packed-Bed Ion-Exchange System to Extract Phytate from Thin Stillage" Membranes 12, no. 2: 230. https://doi.org/10.3390/membranes12020230
APA StyleRodrigues Reis, C. E., & Hu, B. (2022). Volumetric Scale-Up of a Packed-Bed Ion-Exchange System to Extract Phytate from Thin Stillage. Membranes, 12(2), 230. https://doi.org/10.3390/membranes12020230