Calculation of Permeability Coefficients from Solute Equilibration Dynamics: An Assessment of Various Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geometric Parameters
2.2. Model Description
3. Results and Discussion
3.1. Non Ionisable Solutes
3.1.1. Non-Lipophilic Solutes
3.1.2. Lipophilic Solutes
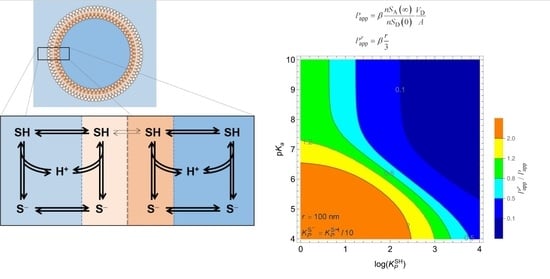
3.2. Weak Acids
3.2.1. Non-Lipophilic Solutes
3.2.2. Lipophilic Solutes
3.3. Following the Solute in the Aqueous Compartment Only
3.4. Intrinsic Permeability Coefficient
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
Estimation of the Bilayer Thickness
Appendix B
Appendix B.1. Calculation of the Local Concentrations for Model I–Non Ionizable Solute
Appendix B.2. Calculation of the Local Concentrations for Model II–Weak Acids
References
- Artursson, P.; Palm, K.; Luthman, K. Caco-2 monolayers in experimental and theoretical predictions of drug transport. Adv. Drug Deliv. Rev. 2012, 64, 280–289. [Google Scholar] [CrossRef]
- Artursson, P.; Karlsson, J. Correlation Between Oral-Drug Absorption in Humans and Apparent Drug Permeability Coefficients in Human Intestinal Epithelial (Caco-2) Cells. Biochem. Biophys. Res. Commun. 1991, 175, 880–885. [Google Scholar] [CrossRef]
- Hellinger, E.; Veszelka, S.; Toth, A.E.; Walter, F.; Kittel, A.; Bakk, M.L.; Tihanyi, K.; Hada, V.; Nakagawa, S.; Thuy, D.H.D.; et al. Comparison of brain capillary endothelial cell-based and epithelial (MDCK-MDR1, Caco-2, and VB-Caco-2) cell-based surrogate blood-brain barrier penetration models. Eur. J. Pharm. Biopharm. 2012, 82, 340–351. [Google Scholar] [CrossRef]
- Pires, C.L.; Praça, C.; Martins, P.A.T.; Batista de Carvalho, A.L.M.; Ferreira, L.; Marques, M.P.M.; Moreno, M.J. Re-Use of Caco-2 Monolayers in Permeability Assays—Validation Regarding Cell Monolayer Integrity. Pharmaceutics 2021, 13, 1563. [Google Scholar] [CrossRef]
- Di, L.; Artursson, P.; Avdeef, A.; Ecker, G.F.; Faller, B.; Fischer, H.; Houston, J.B.; Kansy, M.; Kerns, E.H.; Kramer, S.D.; et al. Evidence-based approach to assess passive diffusion and carrier-mediated drug transport. Drug Discov. Today 2012, 17, 905–912. [Google Scholar] [CrossRef] [PubMed]
- Filipe, H.A.L.; Salvador, A.; Silvestre, J.M.; Vaz, W.L.C.; Moreno, M.J. Beyond Overton’s Rule: Quantitative Modeling of Passive Permeation through Tight Cell Monolayers. Mol. Pharm. 2014, 11, 3696–3706. [Google Scholar] [CrossRef] [PubMed]
- Coreta-Gomes, F.M.; Martins, P.A.T.; Velazquez-Campoy, A.; Vaz, W.L.C.; Geraldes, C.F.G.; Moreno, M.J. Interaction of Bile Salts with Model Membranes Mimicking the Gastrointestinal Epithelium: A Study by Isothermal Titration Calorimetry. Langmuir 2015, 31, 9097–9104. [Google Scholar] [CrossRef]
- Kramer, S.D.; Aschmann, H.E.; Hatibovic, M.; Hermann, K.F.; Neuhaus, C.S.; Brunner, C.; Belli, S. When barriers ignore the “rule-of-five”. Adv. Drug Deliv. Rev. 2016, 101, 62–74. [Google Scholar] [CrossRef]
- Sharifian, M.G. Recent Experimental Developments in Studying Passive Membrane Transport of Drug Molecules. Mol. Pharm. 2021, 18, 2122–2141. [Google Scholar] [CrossRef]
- Eyer, K.; Paech, F.; Schuler, F.; Kuhn, P.; Kissner, R.; Belli, S.; Dittrich, P.S.; Kramer, S.D. A liposomal fluorescence assay to study permeation kinetics of drug-like weak bases across the lipid bilayer. J. Control. Release 2014, 173, 102–109. [Google Scholar] [CrossRef]
- Barbet, J.; Machy, P.; Truneh, A.; Leserman, L.D. Weak Acid-Induced Release of Liposome-Encapsulated Carboxyfluorescein. Biochim. Biophys. Acta 1984, 772, 347–356. [Google Scholar] [CrossRef]
- Henning, R. pH Gradient Across Lysosomal Membrane Generated by Selective Cation Permeability and Donnan Equilibrium. Biochim. Biophys. Acta 1975, 401, 307–316. [Google Scholar] [CrossRef]
- Walter, A.; Hastings, D.; Gutknecht, J. Weak Acid Permeability Through Lipid Bilayer-Membranes—Role of Chemical-Reactions in the Unstirred Layer. J. Gen. Physiol. 1982, 79, 917–933. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hofmann, M.; Schumann, C.; Zimmer, G.; Henzel, K.; Locher, U.; Leuschner, U. LUV’s lipid composition modulates diffusion of bile acids. Chem. Phys. Lipids 2001, 110, 165–171. [Google Scholar] [CrossRef]
- Kramer, S.D. Quantitative aspects of drug permeation across in vitro and in vivo barriers. Eur. J. Pharm. Sci. 2016, 87, 30–46. [Google Scholar] [CrossRef]
- Samelo, J.; Mora, M.J.; Granero, G.E.; Moreno, M.J. Partition of Amphiphilic Molecules to Lipid Bilayers by ITC: Low-Affinity Solutes. ACS Omega 2017, 2, 6863–6869. [Google Scholar] [CrossRef]
- Martins, P.T.; Velazquez-Campoy, A.; Vaz, W.L.C.; Cardoso, R.M.S.; Valerio, J.; Moreno, M.J. Kinetics and Thermodynamics of Chlorpromazine Interaction with Lipid Bilayers: Effect of Charge and Cholesterol. J. Am. Chem. Soc. 2012, 134, 4184–4195. [Google Scholar] [CrossRef]
- Hannesschlaeger, C.; Barta, T.; Pechova, H.; Pohl, P. The Effect of Buffers on Weak Acid Uptake by Vesicles. Biomolecules 2019, 9, 63. [Google Scholar] [CrossRef] [Green Version]
- Sezer, D.; Oruc, T. Protonation Kinetics Compromise Liposomal Fluorescence Assay of Membrane Permeation. J. Phys. Chem. B 2017, 121, 5218–5227. [Google Scholar] [CrossRef]
- Chakrabarti, A.C.; Deamer, D.W. Permeability of Lipid Bilayers to Amino-Acids and Phosphate. Biochim. Biophys. Acta 1992, 1111, 171–177. [Google Scholar] [CrossRef]
- Verkman, A.S.; Dix, J.A.; Seifter, J.L. Water and Urea Transport in Renal Microvillus Membrane-Vesicles. Am. J. Physiol. 1985, 248, F650–F655. [Google Scholar] [CrossRef] [PubMed]
- Lawaczeck, R. Water Permeability Through Biological-Membranes by Isotopic Effects of Fluorescence and Light-Scattering. Biophys. J. 1984, 45, 491–494. [Google Scholar] [CrossRef] [Green Version]
- Paula, S.; Volkov, A.G.; Deamer, D.W. Permeation of halide anions through phospholipid bilayers occurs by the solubility-diffusion mechanism. Biophys. J. 1998, 74, 319–327. [Google Scholar] [CrossRef] [Green Version]
- Thomae, A.V.; Wunderli-Allenspach, H.; Kramer, S.D. Permeation of aromatic carboxylic acids across lipid bilayers: The pH-partition hypothesis revisited. Biophys. J. 2005, 89, 1802–1811. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, P.; Eyer, K.; Allner, S.; Lombardi, D.; Dittrich, P.S. A Microfluidic Vesicle Screening Platform: Monitoring the Lipid Membrane Permeability of Tetracyclines. Anal. Chem. 2011, 83, 8877–8885. [Google Scholar] [CrossRef]
- Hermann, K.F.; Neuhaus, C.S.; Micallef, V.; Wagner, B.; Hatibovic, M.; Aschmann, H.E.; Paech, F.; Alvarez-Sanchez, R.; Kramer, S.D.; Belli, S. Kinetics of lipid bilayer permeation of a series of ionisable drugs and their correlation with human transporter-independent intestinal permeability. Eur. J. Pharm. Sci. 2017, 104, 150–161. [Google Scholar] [CrossRef]
- Venema, K.; Gibrat, R.; Grouzis, J.P.; Grignon, C. Quantitative Measurement of Cationic Fluxes, Selectivity and Membrane-Potential Using Liposomes Multilabelled with Fluorescent-Probes. Biochim. Biophys. Acta 1993, 1146, 87–96. [Google Scholar] [CrossRef]
- Paula, S.; Volkov, A.G.; VanHoek, A.N.; Haines, T.H.; Deamer, D.W. Permeation of protons, potassium ions, and small polar molecules through phospholipid bilayers as a function of membrane thickness. Biophys. J. 1996, 70, 339–348. [Google Scholar] [CrossRef] [Green Version]
- Dordas, C.; Brown, P.H. Permeability of boric acid across lipid bilayers and factors affecting it. J. Membr. Biol. 2000, 175, 95–105. [Google Scholar] [CrossRef]
- Dickson, C.J.; Hornak, V.; Pearlstein, R.A.; Duca, J.S. Structure-Kinetic Relationships of Passive Membrane Permeation from Multiscale Modeling. J. Am. Chem. Soc. 2017, 139, 442–452. [Google Scholar] [CrossRef]
- Deamer, D.W.; Bramhall, J. Permeability of Lipid Bilayers to Water and Ionic Solutes. Chem. Phys. Lipids 1986, 40, 167–188. [Google Scholar] [CrossRef]
- Sanden, T.; Salomonsson, L.; Brzezinski, P.; Widengren, J. Surface-coupled proton exchange of a membrane-bound proton acceptor. Proc. Natl. Acad. Sci. USA 2010, 107, 4129–4134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jing, P.; Rodgers, P.J.; Amemiya, S. High Lipophilicity of Perfluoroalkyl Carboxylate and Sulfonate: Implications for Their Membrane Permeability. J. Am. Chem. Soc. 2009, 131, 2290–2296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sawada, G.A.; Barsuhn, C.L.; Lutzke, B.S.; Houghton, M.E.; Padbury, G.E.; Ho, N.F.H.; Raub, T.J. Increased lipophilicity and subsequent cell partitioning decrease passive transcellular diffusion of novel, highly lipophilic antioxidants. J. Pharmacol. Exp. Ther. 1999, 288, 1317–1326. [Google Scholar]
- Grime, J.M.A.; Edwards, M.A.; Rudd, N.C.; Unwin, P.R. Quantitative visualization of passive transport across bilayer lipid membranes. Proc. Natl. Acad. Sci. USA 2008, 105, 14277–14282. [Google Scholar] [CrossRef] [Green Version]
- Thomae, A.V.; Koch, T.; Panse, C.; Wunderli-Allenspach, H.; Kramer, S.D. Comparing the lipid membrane affinity and permeation of drug-like acids: The intriguing effects of cholesterol and charged lipids. Pharm. Res. 2007, 24, 1457–1472. [Google Scholar] [CrossRef]
- Wolfram Research Inc. Mathematica; Version 12; Wolfram Research, Inc.: Champaign, IL, USA, 2021. [Google Scholar]
- Konig, B.; Dietrich, U.; Klose, G. Hydration and structural properties of mixed lipid/surfactant model membranes. Langmuir 1997, 13, 525–532. [Google Scholar] [CrossRef]
- Greenwood, A.I.; Tristram-Nagle, S.; Nagle, J.F. Partial molecular volumes of lipids and cholesterol. Chem. Phys. Lipids 2006, 143, 1–10. [Google Scholar] [CrossRef] [Green Version]
- MacCallum, J.L.; Bennett, W.F.D.; Tieleman, D.P. Distribution of Amino Acids in a Lipid Bilayer from Computer Simulations. Biophys. J. 2008, 94, 3393–3404. [Google Scholar] [CrossRef] [Green Version]
- Yue, Z.; Li, C.; Voth, G.A.; Swanson, J.M.J. Dynamic Protonation Dramatically Affects the Membrane Permeability of Drug-like Molecules. J. Am. Chem. Soc. 2019, 141, 13421–13433. [Google Scholar] [CrossRef]
- Panahi, A.; Brooks, C.L. Membrane Environment Modulates the pK(a) Values of Transmembrane Helices. J. Phys. Chem. B 2015, 119, 4601–4607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Teixeira, V.H.; Vila-Vicosa, D.; Reis, P.; Machuqueiro, M. pK(a) Values of Titrable Amino Acids at the Water/Membrane Interface. J. Chem. Theory Comput. 2016, 12, 930–934. [Google Scholar] [CrossRef] [PubMed]
- Vila-Vicosa, D.; Silva, T.F.D.; Slaybaugh, G.; Reshetnyak, Y.K.; Andreev, O.A.; Machuqueiro, M. Membrane-Induced pK(a) Shifts in wt-pHLIP and Its L16H Variant. J. Chem. Theory Comput. 2018, 14, 3289–3297. [Google Scholar] [CrossRef] [PubMed]
- Cardoso, R.M.S.; Martins, P.A.T.; Gomes, F.; Doktorovova, S.; Vaz, W.L.C.; Moreno, M.J. Chain-Length Dependence of Insertion, Desorption, and Translocation of a Homologous Series of 7-Nitrobenz-2-oxa-1,3-diazol-4-yl-Labeled Aliphatic Amines in Membranes. J. Phys. Chem. B 2011, 115, 10098–10108. [Google Scholar] [CrossRef]
- Filipe, H.A.L.; Moreno, M.J.; Rog, T.; Vattulainen, I.; Loura, L.M.S. How To Tackle the Issues in Free Energy Simulations of Long Amphiphiles Interacting with Lipid Membranes: Convergence and Local Membrane Deformations. J. Phys. Chem. B 2014, 118, 3572–3581. [Google Scholar] [CrossRef]
- Cardoso, R.M.S.; Filipe, H.A.L.; Gomes, F.; Moreira, N.D.; Vaz, W.L.C.; Moreno, M.J. Chain Length Effect on the Binding of Amphiphiles to Serum Albumin and to POPC Bilayers. J. Phys. Chem. B 2010, 114, 16337–16346. [Google Scholar] [CrossRef]
- Santos, A.; Rodrigues, A.M.; Sobral, A.; Monsanto, P.V.; Vaz, W.L.C.; Moreno, M.J. Early Events in Photodynamic Therapy: Chemical and Physical Changes in a POPC:Cholesterol Bilayer due to Hematoporphyrin IX-mediated Photosensitization. Photochem. Photobiol. 2009, 85, 1409–1417. [Google Scholar] [CrossRef]
- Moreno, M.J.; Prieto, M. Interaction of the Peptide-Hormone Adrenocorticotropin, ACTH(1- 24), with a Membrane Model System—A Fluorescence Study. Photochem. Photobiol. 1993, 57, 431–437. [Google Scholar] [CrossRef]
- Kramer, S.D.; Braun, A.; Jakits-Deiser, C.; Wunderli-Allenspach, H. Towards the predictability of drug-lipid membrane interactions: The pH-dependent affinity of propranolol to phosphatidylinositol containing liposomes. Pharm. Res. 1998, 15, 739–744. [Google Scholar] [CrossRef]
- Balon, K.; Riebesehl, B.U.; Muller, B.W. Drug liposome partitioning as a tool for the prediction of human passive intestinal absorption. Pharm. Res. 1999, 16, 882–888. [Google Scholar] [CrossRef]
- Grunewald, F.; Souza, P.C.T.; Abdizadeh, H.; Barnoud, J.; de Vries, A.H.; Marrink, S.J. Titratable Martini model for constant pH simulations. J. Chem. Phys. 2020, 153, 024118. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Domicevica, L.; Schnell, J.R.; Biggin, P.C. Position and orientational preferences of drug-like compounds in lipid membranes: A computational and NMR approach. Phys. Chem. Chem. Phys. 2015, 17, 19766–19776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klabunde, R.E. Cardiovascular Physiology Concepts, 2nd ed.; Lippincott Williams & Wilkins: Baltimore, MD, USA, 2012; p. 94. [Google Scholar]
- Filipe, H.A.L.; Javanainen, M.; Salvador, A.; Galvao, A.M.; Vattulainen, I.; Loura, L.M.S.; Moreno, M.J. Quantitative Assessment of Methods Used To Obtain Rate Constants from Molecular Dynamics Simulations-Translocation of Cholesterol across Lipid Bilayers. J. Chem. Theory Comput. 2018, 14, 3840–3848. [Google Scholar] [CrossRef] [PubMed]
- Martinotti, C.; Ruiz-Perez, L.; Deplazes, E.; Mancera, R.L. Molecular Dynamics Simulation of Small Molecules Interacting with Biological Membranes. ChemPhysChem 2020, 21, 1486–1514. [Google Scholar] [CrossRef]
- Kramer, A.; Ghysels, A.; Wang, E.; Venable, R.M.; Klauda, J.B.; Brooks, B.R.; Pastor, R.W. Membrane permeability of small molecules from unbiased molecular dynamics simulations. J. Chem. Phys. 2020, 153, 124107. [Google Scholar] [CrossRef]
- Juračka, J.; Šrejber, M.; Melíková, M.; Bazgier, V.; Berka, K. MolMeDB: Molecules on Membranes Database. Database 2019, 2019, baz078. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.; Han, Y.N.; Swanson, J.M.J.; Tan, J.S.; Rose, J.P.; Voth, G.A. Molecular transport through membranes: Accurate permeability coefficients from multidimensional potentials of mean force and local diffusion constants. J. Chem. Phys. 2018, 149, 072310. [Google Scholar] [CrossRef]
- Badaoui, M.; Kells, A.; Molteni, C.; Dickson, C.J.; Hornak, V.; Rosta, E. Calculating Kinetic Rates and Membrane Permeability from Biased Simulations. J. Phys. Chem. B 2018, 122, 11571–11578. [Google Scholar] [CrossRef] [Green Version]
- Sun, R.; Dama, J.F.; Tan, J.S.; Rose, J.P.; Voth, G.A. Transition-Tempered Metadynamics Is a Promising Tool for Studying the Permeation of Drug-like Molecules through Membranes. J. Chem. Theory Comput. 2016, 12, 5157–5169. [Google Scholar] [CrossRef]
- Paloncyova, M.; DeVane, R.; Murch, B.; Berka, K.; Otyepka, M. Amphiphilic Drug-Like Molecules Accumulate in a Membrane below the Head Group Region. J. Phys. Chem. B 2014, 118, 1030–1039. [Google Scholar] [CrossRef]
- Moreno, M.J.; Bastos, M.; Velazquez-Campoy, A. Partition of amphiphilic molecules to lipid bilayers by isothermal titration calorimetry. Anal. Biochem. 2010, 399, 44–47. [Google Scholar] [CrossRef] [PubMed]












| Geometric parameters | 25 nm to 5 μm | Partition coefficients | 1 to 104 | ||
| h | 3.96 to 3.94 nm | 1 to 104 | |||
| 6.4 × 10−17 dm2 [38] | 1 to 104 | ||||
| 1 dm3 | Acidity constants (M) | 10−7 | |||
| 0.76 M−1 [39] | 10−7 | ||||
| Concentrations (M) | 10−3 M | 10−7 or 10−4 to 10−10 | |||
| 10−6 M | |||||
| 0 to 10−4 M | Rate constants (s−1) | 1 s−1 | |||
| 0.01 M | |||||
| 10−7 M | 1 s−1 | ||||
| 10−7 M |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordeiro, M.M.; Salvador, A.; Moreno, M.J. Calculation of Permeability Coefficients from Solute Equilibration Dynamics: An Assessment of Various Methods. Membranes 2022, 12, 254. https://doi.org/10.3390/membranes12030254
Cordeiro MM, Salvador A, Moreno MJ. Calculation of Permeability Coefficients from Solute Equilibration Dynamics: An Assessment of Various Methods. Membranes. 2022; 12(3):254. https://doi.org/10.3390/membranes12030254
Chicago/Turabian StyleCordeiro, Margarida M., Armindo Salvador, and Maria João Moreno. 2022. "Calculation of Permeability Coefficients from Solute Equilibration Dynamics: An Assessment of Various Methods" Membranes 12, no. 3: 254. https://doi.org/10.3390/membranes12030254
APA StyleCordeiro, M. M., Salvador, A., & Moreno, M. J. (2022). Calculation of Permeability Coefficients from Solute Equilibration Dynamics: An Assessment of Various Methods. Membranes, 12(3), 254. https://doi.org/10.3390/membranes12030254