1. Introduction
With the increasing environmental pollution issues and global energy crisis, more and more attention has been paid to green energy resources, particularly hydrogen (H
2) energy [
1,
2]. Though lots of methods have been developed, steam–methane reforming is still the main approach for industrial production of H
2 [
3]. During the steam–methane reforming process, however, the mixture composed of H
2, CO
2, and CH
4 is inevitable, which renders the purification of H
2 highly crucial in hydrogen production. The membrane separation technology is one of the most widely accepted methods for H
2 separation and purification [
4]. Among the reported membranes, two-dimensional (2D) carbon-based membranes have been extensively studied due to their distinct advantages, e.g., low energy consumption and good cyclicity through physical interactions [
5,
6,
7].
Material design by computational methods has been an effective tool to achieve novel 2D carbon-based ultrathin membranes for H
2 separation and purification, especially for the ones with intrinsic pores. As one of the most well-known representatives, the porous graphitic carbon nitride (g-C
3N
4) monolayer has received a lot of attention for its potential as an effective gas separation membrane. Under room temperature, g-C
3N
4 could exhibit extremely high theoretical selectivity for H
2/CH
4 in the order of 10
46 [
8]. Moreover, further theoretical simulations indicated that g-C
3N
4 is also capable in helium (He) purification from both natural gas and noble gas molecules [
9]. With the help of theoretical simulations, the porous C
2N monolayer was reported to be suitable for He separation from other gases (Ne, CH
4, CO
2, etc.) [
10]. Wang et al. investigated the diffusion properties of He, Ne, CO
2, Ar, N
2, CO, and CH
4 through a porous monolayer covalent triazine-based framework (CTF) membrane. Calculation results demonstrate that the selectivity for He and H
2 against common gas molecules (such as CO
2, N
2, CO, and CH
4) is highly promising for practical applications [
11]. Meng et al. theoretically explored the structural and mechanical properties of metal-free fused-ring polyphthalocyanine (H
2PPc) and halogenated H
2PPc (F-H
2PPc and Cl-H
2PPc) membranes. It was found that fluorination and chlorination can effectively tune the permeable pores. Particularly, F-H
2PPc is fascinating as a separation membrane for H
2 purification [
12]. Recently, a series of 2D γ-C
4X (X = O, S, or Se) membranes with intrinsic pores were theoretically designed, among which γ-C
4O shows both low diffusion barriers (0.35 eV) and high permeance (5.0 × 10
−7 mol m
−2 s
−1 Pa
−1) for H
2. Moreover, γ-C
4O is highly promising as a H
2 purification membrane from the H
2/CH
4 mixture with a selectivity of about 10
19 [
13]. The existing studies indicate that there are abundant possibilities for carbon-based ultrathin membranes with intrinsic pores. Therefore, carbon-based membranes with different pore sizes and termination on the pore edges are indispensable for H
2 purification.
Besides the ones entirely composed of non-metal elements, 2D membranes composed of carbon and metal atoms may also play a vital role as gas separation membranes due to the incorporation of metal atoms. In the pioneering work by Li et al., a novel 2D transition metal carbide (h-TMC
6, TM = Mo, W) structure was theoretically designed [
14]. It was found that the crystal structure of h-TMC
6 belongs to the hexagonal Kagome lattice. The stability of h-TMC
6 was confirmed by molecular dynamics simulations and phonon spectra calculations. Later, Liu et al. reported other transition-metal carbides with the same composition of TMC
6 (TM = Mo, W) but a tetragonal lattice [
15], therefore being named s-TMC
6. In general, the TMC
6 monolayers show triple atomic layer structures with Mo/W atomic layers sandwiched between two carbon atomic layers, with TM atoms coordinated with six nearest neighboring C atoms. More importantly, in both h-TMC
6 and s-TMC
6, there are intrinsic pores surrounded by the TM atoms and carbon atoms, whose sizes are mainly determined by the lattice structures.
In this work, the capability of holey structures of TMC6 (M = Mo, W) membranes for H2 purification was theoretically explored, both square and hexagonal phases. By comparing the pore size and separation performance against H2 and other gas molecules (N2, CO, CO2, CH4), it was found that s-TMC6 is more promising for H2 purification, especially from H2/(CO2, CH4) mixtures below room temperature (150–250 K). Our work not only predicts the potential applications of the TMC6 membranes but also recommends the novel membrane materials for H2 purification under low temperature.
3. Results and Discussion
As predicted in previous work, the single-layered TMC
6 (M = Mo, W) includes two different phases with holey structure, namely, the square phase (s-TMC
6) and the hexagonal phase (h-TMC
6). s-TMC
6 shows
P4/mbm symmetry with a lattice constant of 8.541 and 8.543 Å for s-MoC
6 and s-WC
6, respectively. There are 4 TM atoms and 24 carbon atoms in the unit cell of s-TMC
6. Due to the extremely close lattice parameters, s-MoC
6 and s-WC
6 exhibit intrinsic pores with the same diameter of about 5.65 Å, which were obtained by directly measuring from the optimized atomic positions of carbon in the edge of pores. The intrinsic pores are composed of four TM atoms and eight C atoms, as displayed in
Figure 1a. Differently, the h-TMC
6 exhibits
Pm2 symmetry with the lattice constant of 4.381 and 4.383 Å for h-MoC
6 and h-WC
6, respectively. The unit cell of h-TMC
6 contains one TM atom and six carbon atoms. Due to the more compact atomic configurations of h-TMC
6, their intrinsic pores have smaller sizes when compared with s-TMC
6. As indicated in
Figure 1b, the pores in h-TMC
6 are composed of three TM atoms and six C atoms, whose diameters are about 4.48 Å.
After the confirmation of pore structures in the 2D TMC
6, we then tested their performance in gas adsorption and diffusion. In this work, five different kinds of gas molecules (containing H
2, N
2, CO, CO
2, and CH
4) were tested, which are the main components of the gas mixture in the steam–methane reforming process. All the adsorption configurations of gas molecules were fully relaxed. The adsorption energies (
Ead), equilibrium adsorption heights (h), and diffusion barriers (
Eb) are systematically summarized in
Table 1. In the equilibrium configurations, the adsorption heights between the gas molecules and substrate are mostly in the range of 2.0–2.5 Å, along with adsorption energies within −0.18 eV, as shown in
Figure 2a,b. The large adsorption heights and weak adsorption strength evidently indicate physisorption through van der Waals interaction between the gas molecules and TMC
6 substrates. Generally speaking, the
Ead of the same gas molecule on MoC
6 and WC
6 is almost the same, implying the negligible influence of TM atoms on the gas adsorption. Meanwhile, the
Ead values of a gas molecule on s-TMC
6 will be slightly smaller than those on h-TMC
6. However, it is interesting to see that the diffusion of the same molecule on h-TMC
6 will be much more difficult than that on s-TMC
6 due to the much greater
Eb values (see
Figure 2c). Another finding is that for s-MoC
6 and s-WC
6, due to the relatively small
Eb values, the difference between
Eb of the same gas molecule on them is also very small (<0.1 eV). For h-MoC
6 and h-WC
6, a significant difference between
Eb of the same gas molecule on them arises (up to 0.33 eV). Therefore, though the gas molecules have close adsorption interaction on the TMC
6 membranes, their diffusion performance is highly distinguished.
After the comparison of adsorption and diffusion performance of different gas molecules on 2D TMC
6, we then turned to the microscopic insights. As displayed in
Figure 3, the electron density isosurfaces of H
2, N
2, CO, CO
2, and CH
4 at their corresponding transition states are provided with the same isosurface value of 0.015 e Å
−3. For s-TMC
6, it is evident that the smaller pores are fully occupied by the electron density isosurfaces, and the unoccupied parts only appear in larger pores with square shapes. Meanwhile, for h-TMC
6, the triangle shapes appear in the pores as unoccupied parts, whose area is significantly smaller than that in s-TMC
6. As we can see, under the transition states, there is significant overlapping between the electron density distribution of h-TMC
6 and gas molecules, while the overlapping between s-TMC
6 and gas molecules is lower, especially for H
2, N
2, CO, and CO
2. The overlapping of electron density distribution will cause significant electrostatic interactions. The electrostatic interaction plays a leading part during the permeation process because higher overlapping of electron density distribution corresponds to larger E
b values. In this work, the electrostatic interaction mainly originates from the different pore sizes of 2D TMC
6. As a useful tool to quantitatively understand the selectivity of TMC
6 against different gases, a comparison between the measured diameters of the cross section in the van der Waals (vdW) surface (D
c) of different gas molecules and the pore size of unoccupied vdW surface in 2D TMC
6 was also performed. As measured, the unoccupied vdW diameters of pore in s-MoC
6 and s-WC
6 are 2.29 and 2.32 Å, significantly higher than those of g-C
3N
4 (about 1.70 Å) [
8] which results in significantly smaller E
b values for gas molecules permeating g-C
3N
4 when compared with s-TMC
6. As reported, the D
c of H
2, N
2, CO, CO
2, and CH
4 is 2.44, 3.20, 3.46, 3.44, and 3.78 Å, respectively. Therefore, the pore size of s-TMC
6 is very close to the D
c of H
2 but much smaller than those of N
2, CO, CO
2, and CH
4. This finding means that s-TMC
6 will have considerable selectivity against H
2, attributed to the suitable pore size. Notably, though the pore size of s-WC
6 is slightly larger than that of s-MoC
6, it causes higher E
b for the same gas molecule. Hence, the metal species has relatively less influence on the diffusion of gas molecules, but it is not negligible. In the meantime, the unoccupied vdW diameters of pore in h-TMC
6 are 0, which explains why h-TMC
6 exhibits very high diffusion barriers for all the studied gas molecules.
In addition to the comparison between pore sizes, the steric deformation of 2D TMC
6 caused by electrostatic repulsion was also checked. We measured the main bond lengths of different molecules in isolated state (
l1) and TS (
l2), that is, H-H bond length for H
2, N-N bond length for N
2, C-O bond length for CO and CO
2, and C-H bond length for CH
4, taking in consideration the non-polarized structures of CO
2 and CH
4. The comparison between
l1 and
l2 (seeing
Table 1) indicates that the structural changes of the gas molecules under TS are negligible, except for CO and N
2 on h-TMC
6. Then, by removing the gas molecule in its TS structure and calculating the single-point energy (SPE) of the 2D TMC
6, we can obtain the energy differences (Δ
Esub) of the 2D TMC
6 between free-standing state and TS without adsorbates, as listed in
Table 1. It can be summarized that the Δ
Esub is directly proportional to the corresponding
Eb. For H
2, N
2, and CO, the electrostatic repulsion takes the proportion of 10–18% in the
Eb, and the proportion increases to 20–30% for CO
2 and CH
4. It is revealed that CO
2 and CH
4 have more significant electrostatic repulsion with the pore edge of 2D-TMC
6 when compared with other smaller gas molecules. Moreover, as indicated by
Figure 2d, the Δ
Esub in CO
2 involved TS is obviously larger than that in the corresponding CH
4 involved TS, implying stronger electrostatic repulsion of CO
2 to the substrate. This finding explains the origin of the high
Eb values of CO
2 permeating into the pores of 2D TMC
6.
To evaluate the gas separation performance quantitatively, we calculated the permeability and selectivity based on diffusion energy barriers. For the permeability, gas kinetic theory was employed under the ideal gas approximation. Herein, the permeance (
P, in mol m
−2 s
−1 Pa
−1) of the penetrated gases is determined by [
12]
In Equation (1),
Ap denotes the area of the pores, and the total number of collisions per unit time per area (
N) is described as
, where
p,
m,
kB, and
T stand for pressure, the mass of the molecule, the Boltzmann constant, and temperature, respectively. Hence,
ApN could be viewed as the number of molecules that collide with the pore area per unit time. The portion of molecules with a speed large enough to overcome the diffusion barrier through the pore (i.e.,
) is counted as the penetrant portion.
Am,
, and
represent the total area of the membrane, the pressure difference (absolute value) between the two sides of the membrane, and the Maxwell velocity distribution, respectively. It is worth noting that
Am is explicit for a 2D membrane, while
Ap is related to the pore shapes and the effective radii (
Reff) of the atoms at the pore rim. Here,
Reff is calculated as
, where
RvdW denotes the vdW radius. The feed pressure and the pressure difference are
Pa and
Pa as provided in previous work [
24].
The calculated permeance vs. temperature for H
2, N
2, CO, CO
2, and CH
4 passing through the intrinsic pore of s-TMC
6 and h-TMC
6 are displayed in
Figure 4. The green dashed line indicates the industrially acceptable permeance capability for gas separation (green dashed line, 6.7 × 10
−9 mol m
−2 s
−1 Pa
−1). Over the temperature range of 100–500 K, the permeance values for each gas molecule through s-TMC
6 are evidently larger than those through h-TMC
6. s-TMC
6 shows good permeance capability against hydrogen, while h-TMC
6 has low permeance capability for the different gas molecules. Specifically, in the temperature range of 100–300 K, the permeance values of H
2 through s-TMC
6 are always higher than the industrially acceptable one for gas separation. Meanwhile, the permeance values of CO
2 and CH
4 are always lower than the standard. For N
2 and CO, the permeance values will not be higher than the standard until the temperature is higher than 300 K. It is suggested that s-TMC
6 could be a potential H
2 purification membrane to separate H
2 from a mixture composed of N
2, CO, CO
2, or CH
4 below room temperature (100–300 K).
It is well accepted that the performance of a separation membrane is characterized by both the permeance capability and selectivity. Herein, the selectivity between two gas species is defined as the ratio of the diffusion rates,
Sgas-1/gas-2 =
Agas-1/
Agas-2, which comes from the Arrhenius equation:
In Equation (2), the
A0 means the diffusion prefactor that can be taken as the same value for all gases (10
11 s
−1). Based on the definition, the selectivity gradually decreases with the increase in temperature. In
Figure 5, the selectivity versus temperature for H
2/N
2, H
2/CO, H
2/CH
4, and H
2/CO
2 separation by s-MoC
6 and s-WC
6 are illustrated. It is easy to find that the s-TMC
6 membranes mainly exhibit excellent selectivity for H
2/CH
4 and H
2/CO
2 due to the great differences in E
b between H
2 and CH
4/CO
2. Different from other carbon-based 2D membranes, under room temperature (300 K), the selectivity of s-TMC
6 for H
2 against other gas molecules is not ideal enough, with 10
11 and 10
13 for H
2/CH
4 and H
2/CO
2, respectively. It is suggested that s-TMC
6 could be applied as H
2 purification membranes under low temperatures (100–250 K), with the selectivity of H
2/(CO
2, CH
4) larger than 10
15. As indicated by the selectivity, s-WC
6 possesses better H
2 purification ability when compared with s-MoC
6.
The convection–diffusion process is a problem in the field of fluid mechanics. Generally, the finite difference method (FDM) is a major method to treat with the convection–diffusion equation [
25] which only applies to macroscopic systems. However, for microscopic systems such as the TMC
6 membranes in this work, it is extremely difficult to perform quantitative calculations on convection and diffusion of gas flow. As a result, the MD simulations were widely adopted to visualize the time-dependence diffusion process of the molecules, as well as to assess some parameters such as gas diffusion coefficient and the permeated number of gas molecules [
26,
27,
28,
29]. Due to the lack of quantitative results, MD simulations are often applied to confirm the results of DFT calculations.
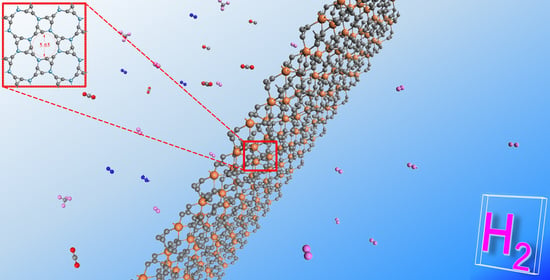
To better understand the transmembrane processes during gas separation, we performed classical MD simulations (at 250 K) on the permeation of gas mixture through the TMC
6 membranes. During the MD simulations, a box of about 4 nm × 4 nm × 12 nm was employed; then, 60 H
2, 60 CO
2, and 60 CH
4 molecules were randomly put into a chamber composed of two TMC
6 membranes (the distance between the membranes was set as 4 nm). In
Figure 6a,b, the number of permeated H
2 molecules versus the simulation time for gas mixture in the chamber composed of s-TMC
6 are depicted. It is found that after MD simulations of 5000 ps, there are 35 and 40 H
2 molecules diffusing outside of the s-MoC
6 and s-WC
6 membranes, respectively. It is worth noting that the diffusion equilibrium was not achieved within 5000 ps; we can expect that after a long enough time, all the H
2 molecules will diffuse through the s-TMC
6 membranes into the product chamber. The snapshots of the gas mixture permeating through the s-TMC
6 membranes at 0 ps, 500 ps, 1000 ps, and 5000 ps are given in
Figure 6c,d. During the permeation process, the H
2 molecules gradually migrate from the feed chamber to the product chamber. Moreover, none of CO
2 or CH
4 is found outside the membranes, clearly indicating that the s-TMC
6 membranes could efficiently separate H
2 molecules from the H
2, CO
2, and CH
4 mixture. Therefore, the MD simulations could well simulate the transmembrane processes of H
2 molecules, which greatly supports our first-principle calculation results.
In addition, it should be mentioned that we also performed the same MD simulations on h-TMC6. However, there are no gas molecules that run out from the chamber after 5000 ps at 250 K, indicating that h-TMC6 could not work as effective gas separation membranes.