Membranes: A Variety of Energy Landscapes for Many Transfer Opportunities
Abstract
:1. Introduction
2. Theoretical Background and Model Development
2.1. Transport of Colloids and Fluid
- the coupling of diffusive flux and migration induced by colloid-membrane interaction describes the Boltzmann exclusion that is due to the colloid-membrane interaction [26]
2.2. Membranes as an Energy Landscape
2.3. Modelling the Transmission and the Counter-Pressure through the Membrane
2.4. Model Application and Validation
3. Impact of Energy Landscape Stiffness
3.1. Impacts of Colloid-Membrane Stiffness on Colloid Transmission
3.2. Asymetric Transmission through a Membrane
- with the flow directed from the bulk to the skin layer of the membrane (the interaction occurs abruptly at the pore entrance)—referred to as forward filtration and corresponding to Figure 5c.
- with the flow directed through the open pores in the substructure before the skin (the interaction with the pore wall take place progressively)—referred to as reverse filtration and corresponding to Figure 5d.
- the forward filtration (through the skin layer supported on the macroporous support Figure 5c) is represented with a thin exclusion layer at the inlet and a thick exclusion layer at the outlet, PeEXi = 0.1 Pe, PeExo = 5 Pe, PePL = PeM = Pe
- the reverse filtration (through the macroporous layer first, Figure 5d) is represented with a thick exclusion layer at the inlet and a thin exclusion layer at the outlet, PeEXi = 5 Pe, PeEXo = 0.1 Pe, PePL = PeM = Pe (thus corresponding to the reversal of the previous case).
3.3. Softer Colloid-Membrane Interaction Ramp Reduces the Separation Energy Cost Asymetric Transmission through a Membrane
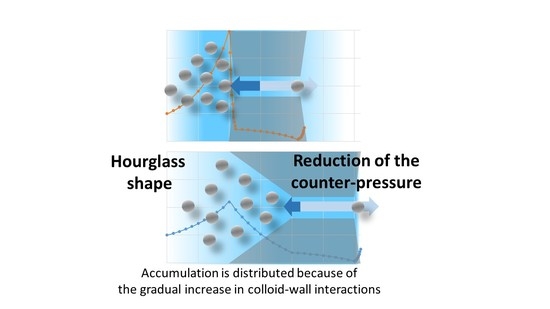
3.4. A New Paradigm: The Accumulation Should Be Distributed
4. Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
References
- Shannon, M.A.; Bohn, P.W.; Elimelech, M.; Georgiadis, J.G.; Mariñas, B.J.; Mayes, A.M. Science and technology for water purification in the coming decades. Nature 2008, 452, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Bocquet, L.; Barrat, J.-L. Flow boundary conditions from nano- to micro-scales. Soft Matter 2007, 3, 685–693. [Google Scholar] [CrossRef]
- Kedem, O.; Katchalsky, A. Thermodynamic analysis of the permeability of biological membranes to non-electrolytes. Biochim. Biophys. Acta 1958, 27, 229–246. [Google Scholar] [CrossRef]
- Bocquet, L.; Charlaix, E. Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 2010, 39, 1073–1095. [Google Scholar] [CrossRef] [PubMed]
- Gravelle, S.; Joly, L.; Detcheverry, F.; Ybert, C.; Cottin-Bizonne, C.; Bocquet, L. Optimizing water permeability through the hourglass shape of aquaporins. Proc. Natl. Acad. Sci. USA 2013, 110, 16367–16372. [Google Scholar] [CrossRef] [PubMed]
- Fermi, E. Thermodynamics; Dover Publications: Mineola, NY, USA, 1937. [Google Scholar]
- Van’t Hoff, J.H. The role of osmotic pressure in the analogy between solutions and gases. J. Membr. Sci. 1995, 100, 39–44. [Google Scholar] [CrossRef]
- Einstein, A. Investigations on the Theory of the Brownian Movement; Courier Corporation: New York, NY, USA, 1956. [Google Scholar]
- Manning, G.S. Binary Diffusion and Bulk Flow through a Potential-Energy Profile: A Kinetic Basis for the Thermodynamic Equations of Flow through Membranes. J. Chem. Phys. 1968, 49, 2668–2675. [Google Scholar] [CrossRef]
- Anderson, J.L.; Malone, D.M. Mechanism of Osmotic Flow in Porous Membranes. Biophys. J. 1974, 14, 957–982. [Google Scholar] [CrossRef]
- Cardoso, S.S.S.; Cartwright, J.H.E. Dynamics of osmosis in a porous medium. R. Soc. Open Sci. 2014, 1, 140352. [Google Scholar] [CrossRef] [PubMed]
- Lachish, U. Osmosis and thermodynamics. Am. J. Phys. 2007, 75, 997–998. [Google Scholar] [CrossRef]
- Nelson, P.H. Osmosis and thermodynamics explained by solute blocking. Eur. Biophys. J. 2017, 46, 59–64. [Google Scholar] [CrossRef] [PubMed]
- Kramer, E.M.; Myers, D.R. Osmosis is not driven by water dilution. Trends Plant Sci. 2013, 18, 195–197. [Google Scholar] [CrossRef] [PubMed]
- Bauer, W.R.; Nadler, W. Molecular transport through channels and pores: Effects of in-channel interactions and blocking. Proc. Natl. Acad. Sci. USA 2006, 103, 11446–11451. [Google Scholar] [CrossRef] [PubMed]
- Zilman, A. Effects of Multiple Occupancy and Interparticle Interactions on Selective Transport through Narrow Channels: Theory versus Experiment. Biophys. J. 2009, 96, 1235–1248. [Google Scholar] [CrossRef] [PubMed]
- Kolomeisky, A.B. Channel-Facilitated Molecular Transport across Membranes: Attraction, Repulsion, and Asymmetry. Phys. Rev. Lett. 2007, 98, 048105. [Google Scholar] [CrossRef] [PubMed]
- Bacchin, P. An energy map model for colloid transport. Chem. Eng. Sci. 2017, 158, 208–215. [Google Scholar] [CrossRef]
- Bacchin, P. Colloid-interface interactions initiate osmotic flow dynamics. Colloids Surf. Physicochem. Eng. Asp. 2017. [Google Scholar] [CrossRef]
- Wales, D. Energy Landscapes; Cambridge University Press: Cambridge, UK, 2004; ISBN 978-0-511-72172-4. [Google Scholar]
- Israelachvili, J.; Wennerström, H. Role of hydration and water structure in biological and colloidal interactions. Nature 1996, 379, 219–225. [Google Scholar] [CrossRef] [PubMed]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids; Courier Dover Publications: New York, NY, USA, 1948; ISBN 978-0-486-40929-0. [Google Scholar]
- Sastry, S.; Debenedetti, P.G.; Stillinger, F.H. Signatures of distinct dynamical regimes in the energy landscape of a glass-forming liquid. Nature 1998, 393, 554–557. [Google Scholar] [CrossRef]
- Vollebregt, H.M.; van der Sman, R.G.M.; Boom, R.M. Suspension flow modelling in particle migration and microfiltration. Soft Matter 2010, 6, 6052. [Google Scholar] [CrossRef]
- Nott, P.R.; Guazzelli, E.; Pouliquen, O. The suspension balance model revisited. Phys. Fluids 1994–Present 2011, 23, 043304. [Google Scholar] [CrossRef]
- Bacchin, P. Dynamics of osmotic flows. arXiv, 2017; arXiv:1705.03248. [Google Scholar]
- Zydney, A.L.; Colton, C.K. A Concentration Polarization Model for the Filtrate Flux in Cross-Flow Microfiltration of Particulate Suspensions. Chem. Eng. Commun. 1986, 47, 1–21. [Google Scholar] [CrossRef]
- Porter, M.C. Concentration Polarization with Membrane Ultrafiltration. Prod. RD 1972, 11, 234–248. [Google Scholar] [CrossRef]
- Cohen, R.; Probstein, R. Colloidal fouling of reverse osmosis membranes. J. Colloid Interface Sci. 1986, 114, 194–207. [Google Scholar] [CrossRef]
- Jönsson, A.-S.; Jönsson, B. Ultrafiltration of Colloidal Dispersions—A Theoretical Model of the Concentration Polarization Phenomena. J. Colloid Interface Sci. 1996, 180, 504–518. [Google Scholar] [CrossRef]
- Bessiere, Y.; Abidine, N.; Bacchin, P. Low fouling conditions in dead-end filtration: Evidence for a critical filtered volume and interpretation using critical osmotic pressure. J. Membr. Sci. 2005, 264, 37–47. [Google Scholar] [CrossRef] [Green Version]
- Bessiere, Y.; Fletcher, D.F.; Bacchin, P. Numerical simulation of colloid dead-end filtration: Effect of membrane characteristics and operating conditions on matter accumulation. J. Membr. Sci. 2008, 313, 52–59. [Google Scholar] [CrossRef] [Green Version]
- Chen, V.; Fane, A.; Madaeni, S.; Wenten, I. Particle deposition during membrane filtration of colloids: Transition between concentration polarization and cake formation. J. Membr. Sci. 1997, 125, 109–122. [Google Scholar] [CrossRef]
- Espinasse, B.; Bacchin, P.; Aimar, P. Filtration method characterizing the reversibility of colloidal fouling layers at a membrane surface: Analysis through critical flux and osmotic pressure. J. Colloid Interface Sci. 2008, 320, 483–490. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bacchin, P.; Aimar, P.; Sanchez, V. Model for colloidal fouling of membranes. AIChE J. 1995, 41, 368–376. [Google Scholar] [CrossRef]
- Bacchin, P.; Marty, A.; Duru, P.; Meireles, M.; Aimar, P. Colloidal surface interactions and membrane fouling: Investigations at pore scale. Adv. Colloid Interface Sci. 2011, 164, 2–11. [Google Scholar] [CrossRef] [PubMed]
- Lomholt, S.; Maxey, M.R. Force-coupling method for particulate two-phase flow: Stokes flow. J. Comput. Phys. 2003, 184, 381–405. [Google Scholar] [CrossRef]
- Agbangla, G.C.; Climent, É.; Bacchin, P. Numerical investigation of channel blockage by flowing microparticles. Comput. Fluids 2014, 94, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Agbangla, G.C.; Bacchin, P.; Climent, E. Collective dynamics of flowing colloids during pore clogging. Soft Matter 2014, 10, 6303–6315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Opong, W.S.; Zydney, A.L. Diffusive and convective protein transport through asymmetric membranes. AIChE J. 1991, 37, 1497–1510. [Google Scholar] [CrossRef]
- Picallo, C.B.; Gravelle, S.; Joly, L.; Charlaix, E.; Bocquet, L. Nanofluidic Osmotic Diodes: Theory and Molecular Dynamics Simulations. Phys. Rev. Lett. 2013, 111, 244501. [Google Scholar] [CrossRef] [PubMed]
- Wijmans, J.G.; Nakao, S.; Van Den Berg, J.W.A.; Troelstra, F.R.; Smolders, C.A. Hydrodynamic resistance of concentration polarization boundary layers in ultrafiltration. J. Membr. Sci. 1985, 22, 117–135. [Google Scholar] [CrossRef]
- Elimelech, M.; Bhattacharjee, S. A novel approach for modeling concentration polarization in crossflow membrane filtration based on the equivalence of osmotic pressure model and filtration theory. J. Membr. Sci. 1998, 145, 223–241. [Google Scholar] [CrossRef]
- Bacchin, P.; Aimar, P.; Sanchez, V. Influence of surface interaction on transfer during colloid ultrafiltration. J. Membr. Sci. 1996, 115, 49–63. [Google Scholar] [CrossRef]
- Jacazio, G.; Probstein, R.F.; Sonin, A.A.; Yung, D. Electrokinetic salt rejection in hyperfiltration through porous materials. Theory and experiment. J. Phys. Chem. 1972, 76, 4015–4023. [Google Scholar] [CrossRef]
- Staverman, A.J. The theory of measurement of osmotic pressure. Recl. Trav. Chim. Pays-Bas 1951, 70, 344–352. [Google Scholar] [CrossRef]
- Elmoazzen, H.Y.; Elliott, J.A.W.; McGann, L.E. Osmotic Transport across Cell Membranes in Nondilute Solutions: A New Nondilute Solute Transport Equation. Biophys. J. 2009, 96, 2559–2571. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Borujeni, E.E.; Zydney, A.L. Use of preconditioning to control membrane fouling and enhance performance during ultrafiltration of plasmid DNA. J. Membr. Sci. 2015, 479, 117–122. [Google Scholar] [CrossRef]
- Volkov, A.V.; Tsarkov, S.E.; Gilman, A.B.; Khotimsky, V.S.; Roldughin, V.I.; Volkov, V.V. Surface modification of PTMSP membranes by plasma treatment: Asymmetry of transport in organic solvent nanofiltration. Adv. Colloid Interface Sci. 2015, 222, 716–727. [Google Scholar] [CrossRef] [PubMed]
- Marquardt, D.; Geier, B.; Pabst, G. Asymmetric Lipid Membranes: Towards More Realistic Model Systems. Membranes 2015, 5, 180–196. [Google Scholar] [CrossRef] [PubMed]
- Caspi, Y.; Zbaida, D.; Cohen, H.; Elbaum, M. Synthetic Mimic of Selective Transport Through the Nuclear Pore Complex. Nano Lett. 2008, 8, 3728–3734. [Google Scholar] [CrossRef] [PubMed]
- Sendekie, Z.B.; Bacchin, P. Colloidal Jamming Dynamics in Microchannel Bottlenecks. Langmuir 2016, 32, 1478–1488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pagliara, S.; Schwall, C.; Keyser, U.F. Optimizing Diffusive Transport Through a Synthetic Membrane Channel. Adv. Mater. 2013, 25, 844–849. [Google Scholar] [CrossRef] [PubMed]
- Locatelli, E.; Pierno, M.; Baldovin, F.; Orlandini, E.; Tan, Y.; Pagliara, S. Single-File Escape of Colloidal Particles from Microfluidic Channels. Phys. Rev. Lett. 2016, 117, 038001. [Google Scholar] [CrossRef] [PubMed]










| Tr | Pe | CP/ | CP (Pa) | ||
|---|---|---|---|---|---|
| Steep ramps | 0.6 | 2.36 | 4.24·10−3 | 0.95 | 3.96 |
| Soft ramps | 0.6 | 1.56 (–34%) | 1.90·10−3 | 1.28 | 2.39 (–40%) |
| Steep ramps | 0.9 | 4.11 | 6.09·10−3 | 0.99 | 5.95 |
| Soft ramps | 0.9 | 2.79 (–34%) | 1.63·10−3 | 1.69 | 2.70 (–55%) |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bacchin, P. Membranes: A Variety of Energy Landscapes for Many Transfer Opportunities. Membranes 2018, 8, 10. https://doi.org/10.3390/membranes8010010
Bacchin P. Membranes: A Variety of Energy Landscapes for Many Transfer Opportunities. Membranes. 2018; 8(1):10. https://doi.org/10.3390/membranes8010010
Chicago/Turabian StyleBacchin, Patrice. 2018. "Membranes: A Variety of Energy Landscapes for Many Transfer Opportunities" Membranes 8, no. 1: 10. https://doi.org/10.3390/membranes8010010
APA StyleBacchin, P. (2018). Membranes: A Variety of Energy Landscapes for Many Transfer Opportunities. Membranes, 8(1), 10. https://doi.org/10.3390/membranes8010010