Application of Artificial Neural Networks to Assess the Mycological State of Bulk Stored Rapeseeds
Abstract
:1. Introduction
2. Materials and Methods
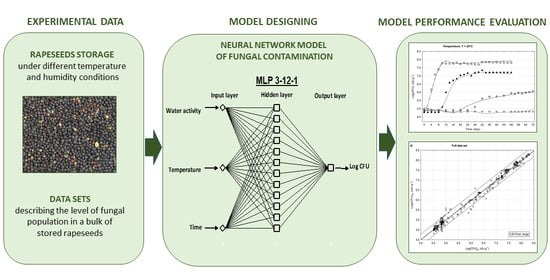
2.1. Experimental Data
2.2. Data Sets Used for Modeling
2.3. Neural Network Models of Mould Contamination
2.4. Model Performance Assessment
3. Results and Discussion
3.1. Neural Network Models of Mould Contamination
3.1.1. Model Based on MLP Networks
3.1.2. Model Based on RBF Networks
3.2. Model Performance Assessment
4. Conclusions
Funding
Conflicts of Interest
References
- Wawrzyniak, J.; Gawrysiak-Witulska, M.; Rudzińska, M. Dynamics of phytosterol degradation in a bulk of rapeseed stored under different temperature and humidity conditions. J. Stored Prod. Res. 2019, 83, 292–304. [Google Scholar] [CrossRef]
- Siger, A.; Gawrysiak-Witulska, M.; Wawrzyniak, J. Changes in contents of phenolic compounds (sinapic acid derivatives) in seeds of Brassica napus L. under adverse storage conditions. Acta Sci. Pol. Technol. Aliment. 2018, 17, 367–375. [Google Scholar] [PubMed]
- Gawrysiak-Witulska, M.; Siger, A.; Wawrzyniak, J.; Nogala-Kalucka, M. Changes in tocochromanol content in seeds of Brassica napus L. during Adverse conditions of storage. J. Am. Oil Chem. Soc. 2011, 88, 1379–1385. [Google Scholar] [CrossRef]
- Sun, K.; Jian, F.; Jayas, D.S.; White, N.D.G. Quality changes in high and low oil content canola during storage: Part I—Safe storage time under constant temperatures. J. Stored Prod. Res. 2014, 59, 320–327. [Google Scholar] [CrossRef]
- Senthilkumar, T.; Jayas, D.S.; White, N.D.G. Detection of different stages of fungal infection in stored canola using near-infrared hyperspectral imaging. J. Stored Prod. Res. 2015, 63, 80–88. [Google Scholar] [CrossRef]
- Wawrzyniak, J.; Gawrysiak-Witulska, M.; Ryniecki, A. Management control points related to the lag phase of fungal growth in a stored rapeseed ecosystem. J. Am. Oil Chem. Soc. 2018, 95, 1223–1235. [Google Scholar] [CrossRef]
- Sujith Kumar, M.S.; Mawlong, I.; Singh, D. Phytosterol recovery from oilseeds: Recent advances. J. Food Process Eng. 2017, 40, e12466. [Google Scholar] [CrossRef]
- Bhat, R.; Reddy, K.R.N. Challenges and issues concerning mycotoxins contamination in oil seeds and their edible oils: Updates from last decade. Food Chem. 2017, 215, 425–437. [Google Scholar] [CrossRef]
- Gancarz, M.; Wawrzyniak, J.; Gawrysiak-Witulska, M.; Wiącek, D.; Nawrocka, A.; Tadla, M.; Rusinek, R. Application of electronic nose with MOS sensors to prediction of rapeseed quality. Measurement 2017, 103, 227–234. [Google Scholar] [CrossRef]
- Gancarz, M.; Wawrzyniak, J.; Gawrysiak-Witulska, M.; Wiącek, D.; Nawrocka, A.; Rusinek, R. Electronic nose with polymer-composite sensors for monitoring fungal deterioration of stored rapeseed. Int. Agrophys. 2017, 31, 317–325. [Google Scholar] [CrossRef] [Green Version]
- Kogkaki, E.A.; Sofoulis, M.; Natskoulis, P.; Tarantilis, P.A.; Pappas, C.S.; Panagou, E.Z. Differentiation and identification of grape-associated black aspergilli using Fourier transform infrared (FT-IR) spectroscopic analysis of mycelia. Int. J. Food Microbiol. 2017, 259, 22–28. [Google Scholar] [CrossRef] [PubMed]
- Marks, B.P. Status of microbial modeling in food process models. Compr. Rev. Food Sci. Food Saf. 2008, 7, 137–143. [Google Scholar] [CrossRef]
- Natskoulis, P.I.; Panagou, E.Z. Predictive modelling of Aspergillus flavus growth and aflatoxins production. In Aflatoxins: Biochemistry, Toxicology, Public Health, Policies and Modern Methods of Analysis; Kintzios, S., Mavrikou, S., Eds.; Nova Science Publishers Inc.: Hauppauge, NY, USA, 2020; pp. 157–206. ISBN 978-1-53616-785-6. [Google Scholar]
- Zwietering, M.H.; Jongenburger, I.; Rombouts, F.M.; Van’t Riet, K. Modeling of the bacterial growth curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baranyi, J.; Roberts, T.A. A dynamic approach to predicting bacterial growth in food. Int. J. Food Microbiol. 1994, 23, 277–294. [Google Scholar] [CrossRef]
- Przybył, K.; Gawałek, J.; Koszela, K.; Wawrzyniak, J.; Gierz, L. Artificial neural networks and electron microscopy to evaluate the quality of fruit and vegetable spray-dried powders. Case study: Strawberry powder. Comput. Electron. Agric. 2018, 155, 314–323. [Google Scholar] [CrossRef]
- Kaya, E.; Saritas, İ. Towards a real-time sorting system: Identification of vitreous durum wheat kernels using ANN based on their morphological, colour, wavelet and gaborlet features. Comput. Electron. Agric. 2019, 166, 105016. [Google Scholar] [CrossRef]
- Nasirahmadi, A.; Behroozi-Khazaei, N. Identification of bean varieties according to color features using artificial neural network. Span. J. Agric. Res. 2013, 11, 670–677. [Google Scholar] [CrossRef] [Green Version]
- Behroozi Khazaei, N.; Tavakoli, T.; Ghassemian, H.; Khoshtaghaza, M.H.; Banakar, A. Applied machine vision and artificial neural network for modeling and controlling of the grape drying process. Comput. Electron. Agric. 2013, 98, 205–213. [Google Scholar] [CrossRef]
- Cinar, I.; Koklu, M. Classification of Rice Varieties Using Artificial Intelligence Methods. Int. J. Intell. Syst. Appl. Eng. 2019, 7, 188–194. [Google Scholar] [CrossRef] [Green Version]
- Ali, S.S.E.; Dildar, S.A. An Efficient Quality Inspection of Food Products Using Neural Network Classification. J. Intell. Syst. 2020, 29, 1425–1440. [Google Scholar] [CrossRef]
- Gu, S.; Wang, J.; Wang, Y. Early discrimination and growth tracking of Aspergillus spp. contamination in rice kernels using electronic nose. Food Chem. 2019, 292, 325–335. [Google Scholar] [CrossRef] [PubMed]
- Adiani, V.; Gupta, S.; Ambolikar, R.; Variyar, P.S. Development of rapid method to assess microbial quality of minimally processed pomegranate arils using FTIR. Sens. Actuators B Chem. 2018, 260, 800–807. [Google Scholar] [CrossRef]
- Siripatrawan, U.; Makino, Y. Monitoring fungal growth on brown rice grains using rapid and non-destructive hyperspectral imaging. Int. J. Food Microbiol. 2015, 199, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Jeyamkondan, S.; Jayas, D.S.; Holley, R.A. Microbial growth modelling with artificial neural networks. Int. J. Food Microbiol. 2001, 64, 343–354. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Safari Sinegani, A.A.; Sarikhani, M.R.; Mohammadi, S.A. Comparison of artificial neural network and multivariate regression models for prediction of Azotobacteria population in soil under different land uses. Comput. Electron. Agric. 2017, 140, 409–421. [Google Scholar] [CrossRef]
- Alghooneh, A.; Alizadeh Behbahani, B.; Noorbakhsh, H.; Tabatabaei Yazdi, F. Application of intelligent modeling to predict the population dynamics of Pseudomonas aeruginosa in Frankfurter sausage containing Satureja bachtiarica extracts. Microb. Pathog. 2015, 85, 58–65. [Google Scholar] [CrossRef]
- Amina, M.; Kodogiannis, V.S.; Petrounias, I.P.; Lygouras, J.N.; Nychas, G.-J.E. Identification of the Listeria monocytogenes survival curves in UHT whole milk utilising local linear wavelet neural networks. Expert Syst. Appl. 2012, 39, 1435–1450. [Google Scholar] [CrossRef]
- Keeratipibul, S.; Phewpan, A.; Lursinsap, C. Prediction of coliforms and Escherichia coli on tomato fruits and lettuce leaves after sanitizing by using Artificial Neural Networks. LWT—Food Sci. Technol. 2011, 44, 130–138. [Google Scholar] [CrossRef]
- Valero, A.; Hervás, C.; García-Gimeno, R.M.; Zurera, G. Product unit neural network models for predicting the growth limits of Listeria monocytogenes. Food Microbiol. 2007, 24, 452–464. [Google Scholar] [CrossRef]
- Yu, C.; Davidson, V.J.; Yang, S.X. A neural network approach to predict survival/death and growth/no-growth interfaces for Escherichia coli O157:H7. Food Microbiol. 2006, 23, 552–560. [Google Scholar] [CrossRef]
- Panagou, E.Z.; Kodogiannis, V.; Nychas, G.J.E. Modelling fungal growth using radial basis function neural networks: The case of the ascomycetous fungus Monascus ruber van Tieghem. Int. J. Food Microbiol. 2007, 117, 276–286. [Google Scholar] [CrossRef] [PubMed]
- Panagou, E.Z.; Kodogiannis, V.S. Application of neural networks as a non-linear modelling technique in food mycology. Expert Syst. Appl. 2009, 36, 121–131. [Google Scholar] [CrossRef]
- Mateo, F.; Gadea, R.; Medina, Á.; Mateo, R.; Jiménez, M. Predictive assessment of ochratoxin A accumulation in grape juice based-medium by Aspergillus carbonarius using neural networks. J. Appl. Microbiol. 2009, 107, 915–927. [Google Scholar] [CrossRef] [PubMed]
- Mateo, F.; Gadea, R.; Mateo, E.M.; Jiménez, M. Multilayer perceptron neural networks and radial-basis function networks as tools to forecast accumulation of deoxynivalenol in barley seeds contaminated with Fusarium culmorum. Food Control 2011, 22, 88–95. [Google Scholar] [CrossRef]
- Aldars-García, L.; Sanchis, V.; Ramos, A.J.; Marín, S. Single vs multiple-spore inoculum effect on growth kinetic parameters and modeled probabilities of growth and aflatoxin B1 production of Aspergillus flavus on pistachio extract agar. Int. J. Food Microbiol. 2017, 243, 28–35. [Google Scholar] [CrossRef]
- Marín, S.; Cuevas, D.; Ramos, A.J.; Sanchis, V. Fitting of colony diameter and ergosterol as indicators of food borne mould growth to known growth models in solid medium. Int. J. Food Microbiol. 2008, 121, 139–149. [Google Scholar] [CrossRef]
- Yogendrarajah, P.; Vermeulen, A.; Jacxsens, L.; Mavromichali, E.; De Saeger, S.; De Meulenaer, B.; Devlieghere, F. Mycotoxin production and predictive modelling kinetics on the growth of Aspergillus flavus and Aspergillus parasiticus isolates in whole black peppercorns (Piper nigrum L.). Int. J. Food Microbiol. 2016, 228, 44–57. [Google Scholar] [CrossRef]
- Garcia, D.; Ramos, A.J.; Sanchis, V.; Marín, S. Predicting mycotoxins in foods: A review. Food Microbiol. 2009, 26, 757–769. [Google Scholar] [CrossRef]
- Magan, N.; Aldred, D. Post-harvest control strategies: Minimizing mycotoxins in the food chain. Int. J. Food Microbiol. 2007, 119, 131–139. [Google Scholar] [CrossRef] [Green Version]
- Mylona, K.; Magan, N. Fusarium langsethiae: Storage environment in fluences dry matter losses and T2 and HT-2 toxin contamination of oats. J. Stored Prod. Res. 2011, 47, 321–327. [Google Scholar] [CrossRef]
- Huang, Y.; Lan, Y.; Thomson, S.J.; Fang, A.; Hoffmann, W.C.; Lacey, R.E. Development of soft computing and applications in agricultural and biological engineering. Comput. Electron. Agric. 2010, 71, 107–127. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, R.J.; Fernández, M.B.; Nolasco, S.M. Artificial neural network model for the kinetics of canola oil extraction for different seed samples and pretreatments. J. Food Process Eng. 2018, 41, e12608. [Google Scholar] [CrossRef]
- López-Aguilar, K.; Benavides-Mendoza, A.; González-Morales, S.; Juárez-Maldonado, A.; Chiñas-Sánchez, P.; Morelos-Moreno, A. Artificial neural network modeling of greenhouse tomato yield and aerial dry matter. Agriculture 2020, 10, 97. [Google Scholar] [CrossRef] [Green Version]
- Mittal, G.S. Artificial Neural Network (ANN) Based Process Modeling. In Handbook of Farm, Dairy and Food Machinery Engineering, 2nd ed.; Kutz, M., Ed.; Academic Press: Cambridge, MA, USA; Elsevier Inc.: Amsterdam, The Netherlands, 2013; pp. 467–473. ISBN 9780123858818. [Google Scholar]
- Te Giffel, M.C.; Zwietering, M.H. Validation of predictive models describing the growth of Listeria monocytogenes. Int. J. Food Microbiol. 1999, 46, 135–149. [Google Scholar] [CrossRef]
- Walther, B.A.; Moore, J.L. The concepts of bias, precision and accuracy, and their use in testing the performance of species richness estimators, with a literature review of estimator performance. Ecography 2005, 28, 815–829. [Google Scholar] [CrossRef]
- Du, C.J.; Sun, D.W. Learning techniques used in computer vision for food quality evaluation: A review. J. Food Eng. 2006, 72, 39–55. [Google Scholar] [CrossRef]
- Sheela, K.G.; Deepa, S.N. Selection of number of hidden neurons in neural networks in renewable energy systems. J. Sci. Ind. Res. 2014, 73, 686–688. [Google Scholar]
- Fernández, J.C.; Hervás, C.; Martínez-Estudillo, F.J.; Gutiérrez, P.A. Memetic Pareto Evolutionary Artificial Neural Networks to determine growth/no-growth in predictive microbiology. Appl. Soft Comput. 2011, 11, 534–550. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Huang, Y. Advances in artificial neural networks—Methodological development and application. Algorithms 2009, 2, 973–1007. [Google Scholar] [CrossRef]
- Zimmermann, M.; Miorelli, S.; Massaguer, P.R.; Falcão Aragão, G.M. Modeling the influence of water activity and ascospore age on the growth of Neosartorya fischeri in pineapple juice. LWT Food Sci. Technol. 2011, 44, 239–243. [Google Scholar] [CrossRef]
- Wawrzyniak, J. A Predictive Model for Assessment of the Risk of Mold Growth in Rapeseeds Stored in a bulk as a Decision Support Tool for Postharvest Management Systems. J. Am. Oil Chem. Soc. 2020. [Google Scholar] [CrossRef]








| Temperature (°C) | Type of Experiments | |
|---|---|---|
| Model Development | Model Validation | |
| Water Activity | ||
| 12 | 0.76 | 0.86 |
| 0.80 | ||
| 0.90 | ||
| 18 | 0.76 | 0.80 |
| 0.86 | ||
| 0.90 | ||
| 24 | 0.75 | 0.85 |
| 0.81 | ||
| 0.90 | ||
| 30 | 0.75 | 0.80 |
| 0.84 | ||
| 0.90 | ||
| Type of Network | Activation Function | |||
|---|---|---|---|---|
| Hidden Layer | Output Layer | |||
| Linear | Logistic | Hyperbolic Tangent | ||
| MLP | Linear | Lin/Lin | Lin/Log | Lin/Tanh |
| Logistic | Log/Lin | Log/Log | Log/Tanh | |
| Hyperbolic tangent | Tanh/Lin | Tanh/Log | Tanh/Tanh | |
| RBF | Gaussian | Gau/Lin | - | - |
| Architecture of Neural Network Model | Activation Function Hidden/Output Layer | Errors | ||
|---|---|---|---|---|
| El | Et | Ev | ||
| MLP 3-12-1 | Tanh/Lin | 0.007 | 0.009 | 0.018 |
| RBF 3-30-1 | Gau/Lin | 0.039 | 0.032 | 0.055 |
| Statistical Index | Type of Model | Data Set | |||
|---|---|---|---|---|---|
| Training | Test | Validation | Full | ||
| Number of Observation Points (N) | 153 | 69 | 74 | 296 | |
| Fitting indicators | |||||
| Coefficient of determination (R2) | MLP | 0.99 | 0.99 | 0.97 | 0.99 |
| RBF | 0.96 | 0.97 | 0.89 | 0.95 | |
| Root mean square error (RMSE) | MLP | 0.12 | 0.14 | 0.19 | 0.14 |
| RBF | 0.28 | 0.25 | 0.33 | 0.29 | |
| Mean absolute error (MAE) | MLP | 0.08 | 0.09 | 0.14 | 0.10 |
| RBF | 0.20 | 0.17 | 0.26 | 0.21 | |
| Bias indexes | |||||
| Bias factor (Bf) | MLP | 1.00 | 1.00 | 0.99 | 1.00 |
| RBF | 1.00 | 1.00 | 1.00 | 1.00 | |
| Mean relative percentage error (MRPE), (%) | MLP | −0.14 | −0.06 | 1.25 | 0.24 |
| RBF | 0.00 | −0.15 | −0.27 | 0.09 | |
| Accuracy indexes | |||||
| Accuracy factor (Af) | MLP | 1.01 | 1.02 | 1.03 | 1.02 |
| RBF | 1.03 | 1.03 | 1.05 | 1.04 | |
| Mean absolute percentage error (MAPE), (%) | MLP | 1.45 | 1.55 | 2.53 | 1.74 |
| RBF | 3.26 | 2.75 | 4.66 | 3.49 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wawrzyniak, J. Application of Artificial Neural Networks to Assess the Mycological State of Bulk Stored Rapeseeds. Agriculture 2020, 10, 567. https://doi.org/10.3390/agriculture10110567
Wawrzyniak J. Application of Artificial Neural Networks to Assess the Mycological State of Bulk Stored Rapeseeds. Agriculture. 2020; 10(11):567. https://doi.org/10.3390/agriculture10110567
Chicago/Turabian StyleWawrzyniak, Jolanta. 2020. "Application of Artificial Neural Networks to Assess the Mycological State of Bulk Stored Rapeseeds" Agriculture 10, no. 11: 567. https://doi.org/10.3390/agriculture10110567
APA StyleWawrzyniak, J. (2020). Application of Artificial Neural Networks to Assess the Mycological State of Bulk Stored Rapeseeds. Agriculture, 10(11), 567. https://doi.org/10.3390/agriculture10110567