Structure-Borne Wave Radiation by Impact and Vibratory Piling in Offshore Installations: From Sound Prediction to Auditory Damage †
Abstract
:1. Introduction
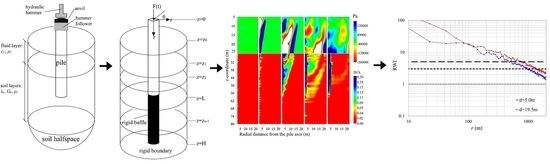
2. Model Description and Governing Equations
3. Wave Radiation during Installation with an Impact Hammer
4. Validation of the Model Predictions
4.1. Reference Measurement at the Anholt site in the Baltic Sea
4.2. Offshore Wind Farm in the German North Sea
4.3. Reference Measurement at the Bard Offshore 1 Construction Site
4.4. Theoretical Benchmark Case: COMPILE
4.5. Concluding Remarks
5. Noise Prediction during Installation with a Vibratory Device
- The response of the system reaches a steady-state regime after a few loading cycles. Here, only a limited number of loading cycles is investigated (nine in total) in order to show the radiated wave pattern and the generated acoustic field. In reality, thousands of loading cycles are needed to install a single pile, and the same response will continue unaltered for longer periods of time.
- The wave field in the soil consists of vertically-polarized shear waves with almost cylindrical fronts that propagate outwards from the vibrating pile with the shear wave velocity in each soil layer. As time advances, the waves in the bottom soil layer are separated from the ones at the upper soil layer due to the difference in the shear wave speed between the two layers, i.e., . This results in an upward bending of the shear fronts at the interface of the two soil layers, which is clearly visible at s.
- The Scholte waves, which propagate parallel to the seabed-water interface, attenuate much less in comparison to the shear waves in the soil. In addition, despite the fact that the maximum amplitude of the exerted force at the top of the pile is reduced by a factor of 20, when compared to the one exerted by the impact hammer (Section 3), the amplitude of the Scholte waves is reduced only by a factor of six. This is related to the fact that the soil responds mainly at low frequencies, which dominate the response in the case of vibratory piling.
- The highest pressures are predicted close to the seabed surface. The typical Mach wave radiation pattern in the fluid region (primary noise path) is not observed in this case. This is in line with the observations and the model developed by Dahl et al. [29] in which the vibratory pile source is modeled as an incoherent line source (and not as a coherent one with a predefined time delay, as was the case when impact piling was examined). As mentioned in [29], any sense of line-source spatial coherency is lost or at the very least rendered vastly more complex with effects not observable in the ensuing pressure field. In other words, the Mach wave radiation from a coherent source traveling down the pile surface is not seen in the case of vibratory piling. On the contrary, the secondary noise path, which consists of the Scholte waves, seems to govern the noise field in the seawater at low frequencies in the vicinity of the seabed surface. This is again in line with the measurements presented in [29], albeit for a different installation setup and pile dimensions, in which it was observed that the Scholte mode contributes to more than 30 dB in the 63-Hz octave band.
- The pressures in the water column are significantly lower when compared to the ones generated by the impact hammer. At this low frequency range, only a few modes propagate in the seawater, i.e., the bulk of the energy irradiates into the soil domain. The contribution of the few propagating modes into the fluid region and its experimental identification are discussed extensively in [29].
6. Zones of Impact for the Aquatic Species
6.1. Impact of Pile Driving Noise on Fish
6.2. Pile Driving Scenarios
- First scenario: The energy input of the hydraulic hammer equals 1000 kJ, and 2000 strikes are required to install the pile;
- Second scenario: The energy input of the hydraulic hammer doubles, i.e., 2000 kJ, and only 1000 strikes suffice to reach the final penetration depth.
6.3. Impact of Pile Driving Noise on Mammals
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- The European Offshore Wind Industry—Key Trends and Statistics 2013; Technical report; The European Wind Energy Association: Brussels, Belgium, 2014; Available online: http://www.ewea.org/fileadmin/files/library/publications/statistics/Europeanoffshorestatistics2013.pdf (accessed on 26 July 2016).
- Gerwick, B.C. Construction of Marine and Offshore Structures, 3rd ed.; CRC Press: San Francisco, CA, USA, 2007; pp. 255–318. ISBN 9781420004571. [Google Scholar]
- Deeks, A.J.; Randolph, M.F. Analytical modeling of hammer impact for pile driving. Int. J. Numer. Anal. Methods Geomech. 1993, 17, 279–302, ISSN 1096-9853. [Google Scholar] [CrossRef]
- Wong, D.; O’Neill, M.W.; Vipulanandan, C. Modeling of vibratory pile driving in sand. Int. J. Numer. Anal. Methods Geomech. 1992, 16, 189–210. [Google Scholar] [CrossRef]
- Bailey, H.; Senior, B.; Simmons, D.; Rusin, J.; Picken, G.; Thompson, P.M. Assessing underwater noise levels during pile-driving at an offshore wind farm and its potential effects on marine mammals. Mar. Pollut. Bull. 2010, 60, 888–897. [Google Scholar] [CrossRef] [PubMed]
- David, J.A. Likely sensitivity of bottlenose dolphins to pile-driving noise. Water Environ. J. 2006, 20, 48–54. [Google Scholar] [CrossRef]
- Madsen, P.T.; Wahlberg, M.; Tougaard, J.; Lucke, K.; Tyack, P. Wind turbine underwater noise and marine mammals: Implications of current knowledge and data needs. Mar. Ecol. Prog. Ser. 2006, 309, 279–295. [Google Scholar] [CrossRef]
- Popper, A.N.; Hastings, M.C. The effects of anthropogenic sources of sound on fishes. J. Fish Biol. 2009, 75, 455–489. [Google Scholar] [CrossRef] [PubMed]
- Damian, H.-P.; Merck, T. Cumulative impacts of offshore windfarms. In Ecological Research at the Offshore Windfarm Alpha Ventus; Federal Maritime, Hydrographic Agency, Nature Conservation Federal Ministry for the Environment, Nuclear Safety, Eds.; Springer Fachmedien: Wiesbaden, Germany, 2014; pp. 193–198. [Google Scholar]
- Erbe, C. International regulation of underwater noise. Acoust. Aust. 2013, 41, 12–19. [Google Scholar]
- Statutory Nature Conservation Agency Protocol for Minimising the Risk Injury to Marine Mammals from Piling Noise; Joint Nature Conservation Committee: Aberdeen, UK, 2010.
- Werner, S. Towards a Precautionary Approach for Regulation of Noise Introduction in the Marine Environment from Pile Driving; Federal Environmental Agency: Stralsund, Germany, 2010. [Google Scholar]
- Lucke, K.; Siebert, U.; Lepper, P.A.; Blanchet, M.-A. Temporary shift in masked hearing thresholds in a harbor porpoise (phocoena phocoena) after exposure to seismic airgun stimuli. J. Acoust. Soc. Am. 2009, 125, 4060–4070. [Google Scholar] [CrossRef] [PubMed]
- Reinhall, P.G.; Dahl, P.H. Underwater mach wave radiation from impact pile driving: Theory and observation. J. Acoust. Soc. Am. 2011, 130, 1209–1216. [Google Scholar] [CrossRef] [PubMed]
- Lippert, S.; Lippert, T.; Heitmann, K.; von Estorff, O. Prediction of underwater noise and far field propagation due to pile driving for offshore wind farms. Proc. Meet. Acoust. 2013, 19. [Google Scholar] [CrossRef]
- Zampolli, M.; Nijhof, M.J.J.; de Jong, C.A.F.; Ainslie, M.A.; Jansen, E.H.W.; Quesson, B.A.J. Validation of finite element computations for the quantitative prediction of underwater noise from impact pile driving. J. Acoust. Soc. Am. 2013, 133, 72–81. [Google Scholar] [CrossRef] [PubMed]
- Lippert, T.; von Estorff, O. The significance of parameter uncertainties for the prediction of offshore pile driving noise. J. Acoust. Soc. Am. 2014, 136, 2463–2471. [Google Scholar] [CrossRef] [PubMed]
- Lippert, T.; Lippert, S. Modeling of pile driving noise by means of wavenumber integration. Acoust. Aust. 2012, 40, 178–182. [Google Scholar]
- Huikwan, K.; Potty, G.R.; Dossot, G.; Smith, K.B.; Miller, J.H. Long range propagation modeling of offshore wind turbine construction noise using Finite Element and Parabolic Equation models. In Proceedings of the OCEANS, Yeosu, Korea, 21–24 May 2012; pp. 1–5.
- Berenger, J.-P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Masoumi, H.R.; Degrande, G. Numerical modeling of free field vibrations due to pile driving using a dynamic soil-structure interaction formulation. J. Comput. Appl. Math. 2008, 215, 503–511. [Google Scholar] [CrossRef]
- Tsouvalas, A.; Metrikine, A.V. A semi-analytical model for the prediction of underwater noise from offshore pile driving. J. Sound Vib. 2013, 332, 3232–3257. [Google Scholar] [CrossRef]
- Tsouvalas, A.; Metrikine, A.V. A three-dimensional vibroacoustic model for the prediction of underwater noise from offshore pile driving. J. Sound Vib. 2014, 333, 2283–2311. [Google Scholar] [CrossRef]
- Deng, Q.; Jianga, W.; Tan, M.; Xing, J.T. Modeling of offshore pile driving noise using a semi-analytical variational formulation. Appl. Acoust. 2016, 104, 85–100. [Google Scholar] [CrossRef]
- Hall, M.V. An analytical model for the underwater sound pressure waveforms radiated when an offshore pile is driven. J. Acoust. Soc. Am. 2015, 138, 795–806. [Google Scholar] [CrossRef] [PubMed]
- Tsouvalas, A. Underwater noise generated by offshore pile driving. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2015; pp. 1–315. [Google Scholar]
- Wilkes, D.R.; Gavrilov, A. Numerical Modeling of Sound Radiation from Marine Pile Driving over Elastic Seabeds. In Fluid-Structure-Sound Interactions and Control; Springer: Berlin; Heidelberg, Germany, 2016; pp. 107–112. [Google Scholar]
- Tsouvalas, A.; Metrikine, A.V. Wave radiation from vibratory and impact pile driving in a layered acousto-elastic medium. In Proceedings of the 9th International Conference on Structural Dynamics (EURODYN 2014), Porto, Portugal, 30 June–2 July 2014; pp. 3137–3144.
- Dahl, P.H.; Dall’Osto, D.R.; Farrell, D.M. The underwater sound field from vibratory pile driving. J. Acoust. Soc. Am. 2015, 137, 3544–3554. [Google Scholar] [CrossRef] [PubMed]
- Halvorsen, M.B.; Casper, B.M.; Woodley, C.M.; Carlson, T.J.; Popper, A.N. Threshold for Onset of Injury in Chinook Salmon from Exposure to Impulsive Pile Driving Sounds. PLoS ONE 2012, 7, e38968. [Google Scholar] [CrossRef] [PubMed]
- Fricke, M.B.; Rolfes, R. Towards a complete physically based forecast model for underwater noise related to impact pile driving. J. Acoust. Soc. Am. 2015, 137, 1564–1575. [Google Scholar] [CrossRef] [PubMed]
- Göttsche, K.M.; Steinhagen, U.; Juhl, P.M. Numerical evaluation of pile vibration and noise emission during offshore pile driving. Appl. Acoust. 2015, 99, 51–59. [Google Scholar] [CrossRef]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics. In Modern Acoustics and Signal Processing; Springer: New York, NY, USA, 2011. [Google Scholar]
- Kaplunov, J.D.; Yu Kossovich, L.; Nolde, E.V. Dynamics of Thin Walled Elastic Bodies; Academic Press: San Diego, CA, USA, 1998; pp. 129–134. [Google Scholar]
- Tsouvalas, A.; van Dalen, K.N.; Metrikine, A.V. The significance of the evanescent spectrum in structure-waveguide interaction problems. J. Acoust. Soc. Am. 2015, 138, 2574–2588. [Google Scholar] [CrossRef] [PubMed]
- Tsouvalas, A.; Metrikine, A.V. Noise reduction by the application of an air-bubble curtain in offshore pile driving. J. Sound Vib. 2016, 371, 150–170. [Google Scholar] [CrossRef]
- Hamilton, E.L. Geoacoustic modeling of the sea floor. J. Acoust. Soc. Am. 1980, 68, 1313–1340. [Google Scholar] [CrossRef]
- Buckingham, M.J. Wave propagation, stress relaxation, and grain-to-grain shearing in saturated, unconsolidated marine sediments. J. Acoust. Soc. Am. 2000, 108, 2796–2815. [Google Scholar] [CrossRef]
- Buckingham, M.J. Compressional and shear wave properties of marine sediments: Comparisons between theory and data. J. Acoust. Soc. Am. 2005, 117, 137–152. [Google Scholar] [CrossRef] [PubMed]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid Saturated Porous Solid: I. Low Frequency Range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid Saturated Porous Solid: II. Higher Frequency Range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Bruns, B.; Stein, P.; Kuhn, C.; Sychla, H.; Gattermann, J. Hydro sound measurements during the installation of large diameter offshore piles using combinations of independent noise mitigation systems. In Proceedings of the Inter-noise 2014 Conference, Melbourne, Australia, 1–10 November 2014.
- Lippert, S.; Nijhof, M.; Lippert, T.; Wilkes, D.; Gavrilov, A.; Heitmann, K.; Ruhnau, M.; von Estorff, O.; Schäfke, A.; Schäfer, I.; et al. COMPILE—A Generic Benchmark Case for Predictions of Marine Pile-Driving Noise. IEEE J. Ocean. Eng. 2016, 1–11. [Google Scholar] [CrossRef]
- MacGillivray, A. A model for underwater sound levels generated by marine impact pile driving. In Proceedings of the 166th Meeting of the Acoustical Society of America, San Francisco, CA, USA, December 2013; Volume 20, pp. 1–12.
- Woodbury, D.P.; Stadler, J.H. A Proposed Method to Assess Physical Injury to Fishes from Underwater Sound Produced During Pile Driving. Bioacoustics 2008, 17, 289–291. [Google Scholar] [CrossRef]
- Roberto, M.; Hamernik, R.P.; Salvi, R.J.; Henderson, D.; Milone, R. Impact noise and the equal energy hypothesis. J. Acoust. Soc. Am. 1985, 77, 1514–1520. [Google Scholar] [CrossRef] [PubMed]
- Stadler, J.H.; Woodbury, D.P. Assessing the effects to fishes from pile driving: Application of new hydroacoustic criteria. In Proceedings of the 38th International Congress and Exposition on Noise Control Engineering (Inter-noise 2009), Ottawa, ON, Canada, 23–29 August 2009.
- Henderson, D.; Subramaniam, M.; Gratton, M.A.; Samuel, S.S. Impact noise: The importance of level, duration, and repetition rate. J. Acoust. Soc. Am. 1991, 89, 1350–1357. [Google Scholar] [CrossRef] [PubMed]
- Hamernik, R.P.; Qiu, W.; Davis, B. The effects of the amplitude distribution of equal energy exposures on noise-induced hearing loss: The kurtosis metric. J. Acoust. Soc. Am. 2003, 114, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Heinis, F.; de Jong, C.A.F.; Rijkswaterstaat Underwater Sound Working Group. Framework for assessing ecological and cumulative effects of offshore wind farms: Cumulative Effects of Impulsive Underwater Sound on Marine Mammals. TNO Report. April 2015. Available online: https://www.noordzeeloket.nl/en/Images/Framework%20for%20assessing%20ecological%20and%20cumulative%20effects%20of%20offshore%20wind%20farms%20-%20Cumulative%20effects%20of%20impulsive%20underwater%20sound%20on%20marine%20mammals_4646.pdf (accessed on 26 July 2016).

















| Parameter | Value | Unit |
|---|---|---|
| E | 210,000 | MPa |
| ν | - | |
| ρ | 7850 | kg·m−3 |
| R | m | |
| L | m | |
| m | ||
| m | ||
| m | ||
| m | ||
| H | m |
| Layer | Depth | ρ | ||||
|---|---|---|---|---|---|---|
| m/m | kg·m−3 | ms−1 | ms−1 | dB/λ | dB/λ | |
| Water | 20 | 1023 | 1453 | − | − | − |
| Fine sand | 8 | 1900 | 1797 | 113 | ||
| Sand-silt-clay | 57 | 1780 | 1635 | 175 |
| Distance | Quantity | Prediction | Scaled Prediction | Measurement | ΔSEL; |
|---|---|---|---|---|---|
| (m) | (2000 kJ) | (350 kJ) | (mean value) | - | |
| 60 | |||||
| 750 | |||||
| Distance | Depth | Quantity | Computed | Measured [31] | ΔSEL |
|---|---|---|---|---|---|
| 10 | 20 | (dB re 1 Pa s) | |||
| 1500 | 38 | (dB re 1 Pa s) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsouvalas, A.; Metrikine, A.V. Structure-Borne Wave Radiation by Impact and Vibratory Piling in Offshore Installations: From Sound Prediction to Auditory Damage. J. Mar. Sci. Eng. 2016, 4, 44. https://doi.org/10.3390/jmse4030044
Tsouvalas A, Metrikine AV. Structure-Borne Wave Radiation by Impact and Vibratory Piling in Offshore Installations: From Sound Prediction to Auditory Damage. Journal of Marine Science and Engineering. 2016; 4(3):44. https://doi.org/10.3390/jmse4030044
Chicago/Turabian StyleTsouvalas, Apostolos, and Andrei V. Metrikine. 2016. "Structure-Borne Wave Radiation by Impact and Vibratory Piling in Offshore Installations: From Sound Prediction to Auditory Damage" Journal of Marine Science and Engineering 4, no. 3: 44. https://doi.org/10.3390/jmse4030044
APA StyleTsouvalas, A., & Metrikine, A. V. (2016). Structure-Borne Wave Radiation by Impact and Vibratory Piling in Offshore Installations: From Sound Prediction to Auditory Damage. Journal of Marine Science and Engineering, 4(3), 44. https://doi.org/10.3390/jmse4030044