Coastal Management Software to Support the Decision-Makers to Mitigate Coastal Erosion

Abstract

There are no sequential and integrated approaches that include the steps needed to perform an adequate management and planning of the coastal zones to mitigate coastal erosion problems and climate change effects. Important numerical model packs are available for users, but often looking deeply to the physical processes, demanding big computational efforts and focusing on specific problems. Thus, it is important to provide adequate tools to the decision-makers, which can be easily interpreted by populations, promoting discussions of optimal intervention scenarios in medium to long-term horizons. COMASO (coastal management software) intends to fill this gap, presenting a group of tools that can be applied in standalone mode, or in a sequential order. The first tool should map the coastal erosion vulnerability and risk, also including the climate change effects, defining a hierarchy of priorities where coastal defense interventions should be performed, or limiting/constraining some land uses or activities. In the locations identified as priorities, a more detailed analysis should consider the application of shoreline and cross-shore evolution models (second tool), allowing discussing intervention scenarios, in medium to long-term horizons. After the defined scenarios, the design of the intervention should be discussed, both in case of being a hard coastal structure or an artificial nourishment (third type of tools). Finally, a cost-benefit assessment tool should optimize the decisions, forecasting costs and benefits for each different scenario, through definition of economic values to the interventions and to the land/services/ecosystems, weighting all the environmental, cultural, social and historical aspects. It is considered that COMASO tools can help giving answers to the major problems of the coastal planning and management entities, integrating transversal knowledge in risk assessment, physical processes, engineering and economic evaluations. The integrated coastal zone management needs these tools to ensure sustainable coastal zones, mitigating erosion and climate change effects.

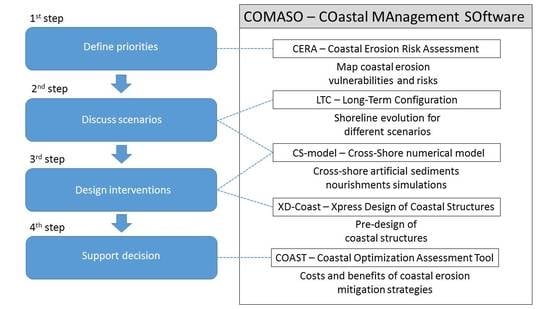
1. Introduction

Coastal erosion is an important problem around the world and requires frequent discussion on mitigation measures and coastal zones management policies [1,2]. In fact, several countries in the world lack an integrated coastal zone management policy capable of assessing the societal goals for a given coastal area [3,4,5,6,7,8]. The typical diagnosis, small-scale, unique and objective, over the coastal system does not produce the best results in the long-term and it should no longer exist [5]. Long-term strategic approaches are needed in coastal governance, including adaptation measures built upon monitoring, multi-criteria and cost–benefit analysis, as a way to deal with opposite interests and challenges within the limits set by the natural dynamics. Only by understanding the ongoing processes behind the natural evolution of such complex and sensitive systems, the vulnerabilities, the risks, the costs, the benefits and impacts of nature–human interactions, managers will be in position to establish a fair decision-making process and reduce the negative impacts of coastal change [4,7]. However, there are no sequential and integrated approaches to guide engineers and managers on the process to develop an adequate management and planning of the coastal zones, capable to tackle coastal erosion and climate change effects. Thus, as a first step to support numerical modeling approaches, providing data and allowing calibration and validation, important monitoring programs should be established. Coastal observatories are recognized as appropriate networks to fight against coastal risks [9]. These authors refer that generally, regional coastal observatories aim to rationalize and mutualize expensively acquired and shared data in regards to coastal risks, in order to respond to public and private requirements for better management of coastal areas. Monitoring programs are considered to improve the context for strengthening the numerical tools that counteract coastal risks.

Important numerical model packs are available for users, but often looking deeply to the physical processes, demanding big computational efforts and focusing on specific problems. Important research on this topic may be referred. Delft University of Technology (The Netherlands) developed SWAN [10], a third-generation wave model that computes random, short-crested wind-generated waves in coastal regions and inland waters. The same institution developed SWASH [11], which is a general-purpose numerical tool for simulating unsteady, non-hydrostatic, free-surface, rotational flow and transport phenomena in coastal waters as driven by waves, tides, buoyancy and wind forces. It provides a general basis for describing wave transformations from deep water to a beach, port or harbor, complex changes to rapidly varied flows and density driven flows in coastal seas, estuaries, lakes and rivers. North Carolina State University (USA) also considers that computational modeling is a crucial tool in the effort to understand coastal processes. They develop models to describe the oceans in deep water and the nearshore, and then validate them against the best available measurements and knowledge of natural behavior. These large-scale models lead to better representations of coastal processes, and thus to improved understanding of the natural and built environments. Their focus is mainly extending model capabilities, through the incorporation of additional physical processes, improving model efficiency, through the use of modern techniques for parallel computing, and communicating model results, through the integration of novel visualization techniques with the needs of end users. MIKE [12,13], powered by Danish Hydraulic Institute (Denmark), is a numerical modeling software to provide maximum versatility and quality in coastal and marine modeling, helping to develop efficient, reliable and sustainable solutions. MIKE products can simulate a range of flow phenomena, waves, sediment dynamics, dispersion phenomena and ecological systems. The two main coast and marine products are MIKE 21 for 2D modeling and MIKE 3 for 3D modeling. Both products have an ample range of application possibilities and are typically used to support coastal engineering and studies related to harbors or similar structures, and environmental applications. CEDAS integrates NEMOS software [14] and it was developed for engineers and scientists in the fields of coastal, ocean and hydraulic engineering, oceanography and geology. It represents a comprehensive collection of coastal engineering design and analysis software developed by or for the Waterways Experiment Station (USA). CEDAS models range from simplified techniques to more sophisticated models for multi-dimensional hydrodynamics, wave propagation, nearshore hydrodynamics and beach processes and inlet technology.

Many other institutions may be referred and it is clear that process-based numerical models have been and still are widely used to describe the complex interaction between waves, tides and sediment transport, and the resulting morphological and shoreline changes. These models are successfully applied for short-term (hours to days) and medium-term (weeks to months) forecasting, such as single or multiple storm events, often at a limited spatial scale associated with specific engineering schemes [15]. Examples of such models include the applications of XBeach for morphological evolutions [16,17,18], and the statistical-process based approach for beach profiles [19]. For the predictions over a longer time and space scales, hybrid modeling, also termed behavior-oriented models have been used as are the cases of the one-line shoreline evolution models [20,21,22,23,24,25] and the cross-shore profile evolution models of [26,27,28]. Process-based models continue to represent valuable insights into complex processes, thus improving their level of understanding [29]. However, it is important to provide proper tools to the decision-makers, which can be easily interpreted by populations, promoting discussions of optimal intervention scenarios in medium to long-term horizons.

COMASO (COastal MAnagement SOftware) intends to fill this gap, presenting a group of tools that can be applied in standalone mode, or in a sequential order (Figure 1). COMASO pack of numerical tools resulted from the collection of the programming work developed since 2000 in the Civil Engineering Department of the Aveiro University, Portugal, in collaboration with an extended group of colleagues of Porto University and National Laboratory of Civil Engineering, in Portugal, and Lund University, in Sweden. COMASO presents five tools: (1) CERA—coastal erosion risk assessment; (2) LTC—long-term configuration; (3) CS-model—cross-shore numerical model; (4) XD-Coast—Xpress design of coastal structures; and (5) COAST—coastal optimization assessment tool. The main goal of COMASO is to support decision-makers on coastal management, planning and engineering practices, presenting four steps of adequate procedures. The first tool also represents the first management step and should map the coastal erosion vulnerability and risk, also including the climate change effects, defining a hierarchy of priorities where coastal defense interventions should be performed, or constraining some land uses or activities. In the second step, in the locations identified as priorities, a more detailed analysis should considerer the application of shoreline and cross-shore evolution models (second and third tools), allowing discussing intervention scenarios, in medium to long-term horizons. After the defined scenarios, the third management step should discuss the design of the intervention, both in cases of soft or hard engineering intervention solutions (third and fourth tools). Finally, in the fourth management step, a cost–benefit assessment tool (fifth tool) should optimize the decisions, forecasting costs and benefits for each different scenario, through definition of economic values to the interventions and their maintenance along time, and to the land/services/ecosystems, weighting all the environmental, cultural, social and historical aspects. This paper presents a brief review of coastal modeling tools and discusses the procedures considered important in the coastal management and planning, presenting the sequence of tools brought in COMASO. Note that each tool requires different data, and consequent calibration and validation procedures and thus, for a deeper description of each tool and their previous applications, additional bibliography is recommended along the manuscript.

2. Mapping Vulnerability and Risk

It is important to have access to tools or methods that allows us to map coastal erosion vulnerabilities and risk, and related climate change effects. A method to identify and highlight the priorities of intervention in a simple and low data demanding process is considered a relevant tool in the coastal management process. Depending on the science and context that is studying risk, the interpretation process of this concept takes numerous outcomes [30]. The perspective of risk terminology has been evolving along the years [31], mainly revolving around concepts of probability, uncertainty and expected consequences. The most core and widely accepted definition of risk is to be understood as the expected consequences associated with a given event [32]. On the other hand, the risk is defined as the effect of uncertainty on objectives and is often characterized by reference to potential events or consequences, or a combination of both (Figure 2) [33]. The United Nations supports this definition by stating that risk is a combination of the probability of an event and its negative consequences [34]. Risk is the actual exposure of something of human value to a hazard [35], but these authors also state that is often measured as the product of probability and loss.

2.1. Coastal Risk Assessment Methods

To classify and map coastal risk to support decision-makers started about 30 years ago. The oldest coastal assessment methodology found in the literature was presented in 1991 by the Intergovernmental Panel on Climate Change (IPCC) [36]. Since then, several methodologies were developed, mainly focused on sea-level rise (SLR) and its consequences for coastal zones around the world. In the last decade, in addition to the more traditional methodologies to evaluate coastal risk, several GIS-based (geographic information system) coastal risk assessment tools were developed, mainly to evaluate the impacts of sea-level rise in coastal areas. Many of these GIS-based applications integrate decision support systems (DSS) in their methodologies and aim to help coastal managers in the process of decision making.

Table 1. Risk assessment methodologies and their correspondent objective [30].

Name	Year	Reference	Objective
IPCC Common Methodology (CM)	1991	[36]	Assessment of potential coastal impacts of sea-level rise and adaptation measures
Aerial Videotape-Assisted Vulnerability Analysis (AVVA)	1992	[37]	Assessment of coastal vulnerability to sea-level rise
Coastal Vulnerability Index (CVI)	1999	[38]	Assessment of relative vulnerability of the coast to changes due to sea-level rise
Coastal Vulnerability and Risk Assessment (CVRA)	2005	[39]	Assessment of coastal vulnerability and risk to coastal erosion
Smartline (SL)	2006	[40]	Physical and social vulnerability assessment to coastal erosion and flooding and resulting coastal risk
Tyndall Coastal Simulator (TCS)	2000	[41]	Determining geomorphological response to climate change and its effects on coastline evolution
Dynamic and Interactive Vulnerability Assessment (DIVA)	2004	[42]	Assessment of coastal vulnerability for user-selected climatic, and socio-economic scenarios and adaptation strategies
Decision Support System for Coastal Climate Change Impact (DESYCO)	2005	[43]	Assessment of climate change impacts on coastal areas and related ecosystems
SimCLIM (SC)	2005	[44]	Simulation of bio-physical impacts and socio-economic effects of climatic variations
THESEUS DSS	2009	[45]	Assessment of vulnerability, impacts and risks of coastal areas and identification and evaluation of coastal adaptation options
Coastal Hazard Wheel (CHW)	2012	[46]	Assessment of coastal hazard level for multi-hazard scenarios
RISC-KIT Coastal Risk Assessment Framework 1 (CRAF1)	2013	[47]	Assessment of hazard, exposure and risk of coastal zones for identification of high-risk segments

summarizes some of the methodologies identified by [30].

Additionally to the references presented by [30], other studies related to index-based methodologies can be mentioned, highlighting the importance of defining the priority of interventions. A detailed analysis of available methods (indicators, index, GIS and model based methods) that can be concretely applied for assessing coastal vulnerability to climate change at the European and Regional Sea levels is provided by [48]. A multi-scale coastal risk index for local scale (CRI-LS) in the coast of Morocco was applied by [49]. These authors considered that the local scale approach provides a useful tool for local coastal planning and management by exploring the effects and the extensions of the hazards and combining hazard, vulnerability and exposure variables in order to identify areas where the risk is relatively high. Other authors [50,51] have also performed vulnerability and risk analysis applied to the Italian coast. Finally, a spatial modeling approach applied to UK was presented by [52], which draws together a range of key criteria into a single framework to identify marine areas, which should be prioritized for management and monitoring.

The identified methodologies present a wide range of processes, indicators and scope, both in time and spatial scale, to assess coastal risk, hazards and/or vulnerability. The increase of complexity is noticeable along time. According to [30], common methodology (CM) and aerial videotape-assisted vulnerability analysis (AVVA) are essentially guidelines that lean on local expert knowledge to perform first-order assessments on vulnerable areas. Then, coastal vulnerability index (CVI), coastal vulnerability and risk assessment (CVRA) and the Smartline use a series of established physical, social and environmental indicators to perform the assessment. However, the output differs in the range of classes and in the meaning of those outputs. CVI presents four levels of relative vulnerability, while CVRA considers five levels of vulnerability, value and risk output. On the other hand, the Smartline has six levels of physical vulnerability and 4 risk levels. Finally, the remaining seven identified methodologies go beyond the development of a framework and incorporate software-based tools to assess coastal risk. These methods are mainly based on chains of models that simulate the coastal risk propagation. Although there are some exceptions (i.e. SimCLIM), these models are usually simplified to save on computational costs and due to the data requirements of more complex models.

According to [30], the spatial scale that each methodology can cover is an important feature. On one hand, assessing a large area means getting information about coastal risk for a much larger community. Being capable of evaluating different environments on the same assessment brings benefits in terms of classification comparison and prioritization of hotspots for the application of mitigation measures. The capacity of assessing large areas is good for national land-use planning, which usually requires assessments for large areas with limited deadlines. However, assessing coastal risk at a global scale can lead to a lack of detail and inaccurate or outdated data regarding certain areas, resulting in a less accurate risk evaluation on those areas.

The coastal risk assessment in a medium and long-term period could provide the information for a more thoughtful coastal management, supporting the execution of coastal interventions aiming at long-term development of the area. Thus, the first tool integrating COMASO is CERA (coastal erosion risk assessment) and intends to use simple data to assess coastal erosion risk instead of relying on complex models to estimate future behavior of a coastal zone. This approach will not allow long-term scenario generation, but will provide decision support for proper coastal management in its current state, mainly for developing countries, where complex models can be difficult to apply.

2.2. Coastal Erosion Risk Assessment: CERA

According to [30], in risk management, concepts of coastal vulnerability, exposure, susceptibility, among others, join the intricacy of risk definitions, leading to difficulties and variations in their understanding and relation to each other’s. Vulnerability is defined by the United Nations as the characteristics and circumstances of a community, system or asset that make it susceptible to the damaging effects of a hazard [34]. Moreover, vulnerability as inherent characteristics of a system that create the potential for harm, but are independent of the probabilistic risk of occurrence was described by [53]. Vulnerability as a characteristic of a system that describes its potential to be harmed was defined by [54]. However, the term vulnerability is often used in a broader sense depending on the subject. The remaining concepts are more consensual in their meaning. Hazard as a dangerous phenomenon, substance, human activity or condition that may cause loss of life, injury or other health impacts, property damage, loss of livelihoods and services, social and economic disruption or environmental damage was defined by [34]. Exposure is defined by [54], as the quantification of the receptors that may be influenced by a hazard, while [34] considers it as the people, property, systems or other elements present in hazard zones that are thereby subject to potential losses.

The source-pathway-receptors-consequence (SPRC) model [54] was adapted by [30], from coastal flooding to coastal erosion, to propose CERA. This model is used to link various components of a system, helping in the identification of how risk propagates. Therefore, for risk to arise, it must exist a source that triggers the hazard, a pathway that the hazard takes until reaches the receptor, which may be harmed by it, culminating in the consequence provoked by the hazard (Figure 3). Using the SPRC model, each part of the model corresponds to a component of risk estimation [55]. Therefore, an assessment on source conditions should be done to evaluate the hazard probability. A pathway assessment correlates to the degree of exposition and a study of the receptor is required to evaluate how susceptible they are to the hazard. The consequence will vary depending on the value present in the study area.

CERA follows closely the risk concepts of source-pathway-receptors-consequence (SPRC) model [54], by dividing the risk assessment in components of the system:

• Hazard (source)—intensity and/or likelihood of coastal erosion and/or driving sources of coastal erosion (waves, sea-level rise, extreme events);
• Exposure (receptors)—quantification of the receptors that are within range of potential land loss. The exposure assessment can be executed into levels of exposure, classifying receptors from highly exposed to low exposition;
• Susceptibility (pathway)—intrinsic characteristics of the land that makes it predisposed to be eroded by action of wave climate. The susceptibility is independent of the wave conditions at the study area;
• Value (consequence)—valorization of the territory, depending on economic, social, patrimonial and/or environmental factors;
• Vulnerability—the amount of potential damage caused by coastal erosion. Therefore, vulnerability is dependent of the soil predisposition to erode (susceptibility) and the value attributed to that same area. Vulnerability is independent of coastal erosion conditions and exposure level affecting the study area;
• Consequences—potential harm if coastal erosion affects the study area, combining exposure and vulnerability. Contrary to vulnerability, which is independent of exposure, the consequences include exposure to estimate the amount of area that is going to be affected by coastal erosion;
• Risk—a combination between the potential damage that erosion can cause and the likelihood/intensity that coastal erosion affects the study area.

Thus, the assessment process was divided into four different and independent modules: hazard; exposure; susceptibility; value. Each module produces a classification. Next, the modules’ outputs are combined to produce classifications (vulnerability and consequence), culminating in the risk classification. Although modules can be processed in any desired order, CERA framework performs the assessment in the inverted order of SPRC. Hence, the susceptibility module assesses how prone is the territory (i.e., receptor) to be affected by coastal erosion and the value module assesses the socio-economic relevance of that territory, the exposure module assesses the obstacles that coastal erosion must surpass (i.e., pathway) to reach the territory in evaluation and the coastal erosion module assesses how likely and/or intense is coastal erosion (i.e., sources) in the study area. A total of 12 indicators within the four modules were considered [30].

CERA presents an inland classification, being suitable for stakeholder communication and compatible with area delimitation asked by government programs. Overall, CERA corresponds to a coastal erosion risk assessment methodology for medium-term, based on current indicators. The methodology is flexible enough to be applicable to a wide range of coastal environments and scales, with variable accuracy, depending on the input data. Moreover, the methodology has an accessible process that avoids numerical modeling and can be replicated by interested users and stakeholders without major resources required. A GIS-based application was developed and can be used freely within QGIS, a free and open-source software, boosting the accessibility of the methodology. CERA was already successfully applied to different sandy coasts in the world, where it was possible to compare the tool performance in different scales of application. CERA applications to Aveiro coast (Portugal), Macaneta (Mozambique) and Quintana Roo (México) were presented by [30,56], where the extension of the coast ranged from about 12 to about 250 km. CERA was also applied to the Venice coast, in the Mediterranean [57]. More information about CERA can be found in [30,56].

3. Forecasting Shoreline and Profile Evolution

To proceed with an adequate management at the vulnerable and risk areas identified in the previous management step, it is considered important to forecast the shoreline evolution and the cross-shore beach profiles under alternative scenarios of wave climate and climate change effects and intervention options. Thus, in support of coastal engineering and management activities, sophisticated, robust and reliable models for simulating coastal evolution over decades to centuries have been pursued. The earliest type of long-term coastal evolution models focused on predicting the shoreline evolution in response to the potential sediment transport gradient generated by incident wave energy, following the one-line theory. According to this theory, firstly introduced by [20] and numerically implemented by numerous authors since then, the beach profile moves parallel to itself, maintaining an equilibrium configuration. Thus, one contour line can be used to describe changes in the beach shape and the associated volume during accretionary and erosional events. Some examples of such models are GENESIS [58], Unibest CL + by Deltares, LITPACK (LITLINE) by Danish Hydraulic Institute (DHI) and LTC [39]. Although, these models can be used at large temporal (annual–decadal) and spatial scales (kilometers), one of their weaknesses has been the simplified representation of the cross-shore (CS) material exchange, where usually CS processes are incorporated through sink or source terms, with representative values in time and space [7,28].

3.1. Shoreline Long-Term Configuration: LTC

The one-line theory models help to discuss different intervention scenarios when compared with a no intervention scenario, allowing testing different solutions and evaluating their adequate characteristics to improve the physical performance of artificial nourishment, groin, longitudinal revetment or detached breakwater. These models have been successfully applied to simulate shoreline response to wave and current actions [59], and the one-line theory has had a great development through [58], with GENESIS. One-line models used to estimate longshore sand transport rates and long-term shoreline changes generally assume that the profile is displaced parallel to itself in the cross-shore direction (Figure 4). These models are formulated based on the conservation equation of sediments in a control volume or shoreline stretch and on an alongshore sand transport equation [60]. It is assumed that there is an offshore depth of closure and an onshore upper end of the active profile, defining the limits where no significant changes happen [25]. The constant profile shape moves in the cross-shore direction between these two limits, implying that sediment transport gradients are uniformly distributed over the active portion of the profile [61].

COMASO considers LTC (long-term configuration) as an adequate model to define the shoreline evolution in time horizons of 10–50 years, in coastline extensions up to 10 km. This tool is important to support the cost–benefit analysis defined as the last step of COMASO tools. LTC was primary developed by [39], at Aveiro University, Portugal, to support coastal zone planning and management in relation to coastal erosion problems. Since then, the model has been improved and extensively applied. LTC combines a simple classical one-line model with a rule-based model for erosion/accretion volumes distribution along the beach profile [25,62]. This model was designed for sandy beaches, where the main cause of shoreline evolution is the alongshore sediment transport gradients, dependent on the wave climate, water levels, sediment sources and sinks, sediment characteristics and boundary conditions. The model inputs are the wave climate, water level and the bathymetry and topography of the landward adjacent zones (updated during calculation). The accuracy of the model is dependent of good input data (to calibrate and validate results), only achieved by frequent and consistent monitoring programs. The sediment transport volumes are estimated by formulae that consider the shoreline’s angle to oncoming breaking waves and the breaking wave height (CERC formula). The sediment volume variation in a coastal stretch is caused by sediment transport gradients between modeled cells where, similar to one-line models, the balance of volumes is defined through the continuity equation. LTC assumes a uniform cross-shore distribution of the alongshore sediment transport along the active width of the cross-shore profiles, thus performing a uniform variation of the vertical coordinates of the active profile grid points, adjusting the active profile at the boundaries based on the sediments friction angle defined by the users. This way, the variation of the shoreline position depends, not only, on the sediment volume variation, but also, on the topography and bathymetry associated with each cross-shore profile. With the LTC numerical model, the 3D topo-hydrographic data are continuously updated during simulation, allowing the model to distribute erosion or accretion sediment volumes for each wave action (computational time step). Moreover, different coastal protection works combinations may be considered with almost no limitation for the number of groins, breakwaters and seawalls, the number of sediment sources/sinks sites, and artificial nourishments [39]. The Portuguese Northwest coast was simulated with LTC in different scenarios, considering both scientific and consultant purposes. The calibration and validation of the model results in each study was dependent of longshore sediment transport and shoreline position variation rates registered in the past. An overview of the LTC applications performed to real situations was presented by [62], highlighting the main achievements of each study. LTC model can continue to be developed and may integrate complementary tools, which together with the design of interventions and the analysis of its costs and benefits will facilitate the identification of adequate coastal erosion mitigation scenarios, helping on planning and management of the coastal zones.

3.2. Cross-Shore Modelling: CS-Model

Profile evolution models are commonly used to simulate the beach change on a short-term basis (hours to days), for investigating the impact of storms in the beach-dune system evolution, as well as the response of beach fills under storm conditions [7], e.g., SBEACH [63], LITPACK (LITPROF) by DHI, XBEACH [16], but also on a short to medium-term (month to year) like Unibest TC, by Deltares. These numerical models have been designated as cross-shore profile models, taking into account cross-shore sediment transport processes but neglecting any differentials in the longshore direction. During a storm such a simplification is normally of adequate accuracy for engineering applications [28,64]. Nearshore morphology models simulating storm-induced changes have been widely applied for the last decade and demonstrated an acceptable level of accuracy as a result of well-defined cross-shore sediment transport equations, established numerical solutions, and high-quality field and laboratory data [65].

The beach-dune system is one of the most important natural coastal protections in low-lying and sandy shores. However, as dynamic natural system, impacts of single storm events (characterized by a considerable rise of the water level and energetic wave heights) can trigger episodes of erosion-overtopping-breaching-flooding, causing irreversible losses for natural environments and adjacent urban infrastructures [7]. Over the last decades, large efforts have been made to predict the impact of these extreme events, through the understanding and analytical reproduction, using numerical models, of the main physical processes involved in the coastal morphodynamic system [28,63,66,67].

Currently, profile models cannot simulate the beach recovery process on the post-storm scale. So, applying profile response models typically intend to predict beach and dune erosion produced by severe storms or hurricanes, and evaluate initial adjustment of beach fills to wave action and/or fill losses during a storm [68]. The typical timescale of profile response models is hours to days for a storm event, whereas if long-time beach recovery or fill adjustment is investigated a timescale of months is of interest [7]. For that reason, several model approaches have been developed to address these timescales: models using equilibrium concepts; empirical and semi-empirical models; process-based models (also termed as “deterministic”); behavior oriented models and data-driven models based on statistical analysis [69,70].

According to [28], to improve the predictive capabilities of coastal evolution models, physics-based formulations need to be employed for calculating CS exchange, although schematizations of the governing processes are required to reduce the computational effort. A proper balance between physical descriptions from theoretical considerations and empirical information based on data and observations is the key for simulations addressing large areas and long time periods, which will yield useful simulations results. Larson et al. [66] developed a semi-empirical model to simulate the long-term response of longshore bars to incident wave conditions, as well as the material exchange between the berm and bar region. In this model, the variation in the bar volume is taken to be proportional to the deviation from its equilibrium condition and it is coupled to the berm response (i.e., bar growth implies a decrease in the berm volume and vice-versa). Subsequently, this model was combined with modules to calculate dune erosion, overwash and wind-blown sand (forming a unique-coupled system) [28], in order to simulate the evolution of a schematized profile at a decadal scale. As a first attempt towards modeling regional cross-shore evolution, all of these merged modules gave rise to the CS-model, a cross-shore profile numerical model developed to fill the gap between a sediment budget approach and a detailed profile evolution model.

A detailed description about the theoretical developments of the cross-shore numerical model (CS-model) can be consulted in [28]. This model was developed to simulate the cross-shore exchange of sand and the resulting profile response at a decadal scale by taking into account the main relevant cross-shore processes in a long-term perspective: dune erosion and overwash, wind-blown sand transport, and bar-berm material exchange. Each one of these processes corresponds to an individual module integrated in the CS-model, which contain physically based algorithms that have been validated against laboratory and field data [28]. In order to model the long-term profile response, a set of sand volume conservation equations are employed and solved together with cross-shore transport equations to describe the evolution of key morphological features. It is assumed that the cross-shore sediment transport, causing changes in the profile shape, is induced by the power of waves and winds, and depends also on the still water levels. These changes, detailing the profile response, are geometrically prescribed so the schematization of the profile type is safeguarded, but the key parameters are changing with time (Figure 5).

The CS-model was successfully tested to several real situations in Portugal, Mozambique and Sweden [6], considering a representative cross-section and monitoring data collected from regular surveys. Artificial nourishment scenarios were also tested in real situations based on data collected in USA [7].

4. Design of Interventions

After evaluating what would be the impacts of different interventions in the shoreline evolution, the design of those interventions should be evaluated. The third COMASO tool comprise two models: one is the presented CS-model, to perform the analysis of artificial nourishments, allowing us to discuss the location, volumes and frequency of filling operations and correspondent longevity of the nourishment in the cross-section; the other, to design hard coastal structures, as groins, longitudinal revetments and detached breakwaters, defining the weight of the blocks required for the resistant layer and the cross-section geometry of the structure. These tools allow a preliminary definition of different intervention scenarios costs along the time span of the coastal management plans.

4.1. Artifitial Nourishments

According to [7], the CS-model has driven to useful simulations detailing the evolution of distinct fill design schemes and determining the time scale and movement of the fill material. Regarding the cross-shore exchange of nourished material, most of the nourishment schemes differed mainly concerning the time evolution of profile adjustment towards a new equilibrium state (which is dependent on the fill volume and placement), whereas the equilibrium states themselves were similar. Due to the coupling between the berm and the bar, placement along the profile and at the bar showed similar behavior, quickly reaching the same equilibrium states (typically during one seasonal cycle). On the contrary, simulation of dune nourishment indicated that the material remains high up in the profile, requiring longer periods to adjust compared to the other schemes, being highly dependent on the occurrence of energetic events to redistribute the nourished sand. An increase in the berm height acted as an additional dune protection against storms, since the probability of waves reaching the dune decreases, preventing erosion. After a specific nourishment volume, the profile does not benefit from an increased fill volume [7]. The schemes tested with different placement frequencies tend to reach similar values for the berm position (y_B) after the same nourishment volume has been placed in the profile. However, integrating the beach width in time, the concentrated fill presented larger accumulated beach width, implying protection during a longer time period.

Different types of nourishments may serve different purposes [7]. To strengthen the dune system over time, berm nourishment may be an appropriate solution, decreasing the probability of the waves reaching the dune foot and also promoting the build-up of the dune by wind. To protect the area around the shoreline on a short-term basis (e.g., when emergency operations due to storm damage are required), nourishment of the profile or at the bar may be suitable to get a faster cross-shore distribution of the fill. Finally, a long-term solution would be dune nourishment, where a storm surge will gradually distribute the fill material along the profile, increasing the berm width until new equilibrium condition prevails.

An extended version of the subaqueous module integrating the main algorithm of the CS-model to calculate bar-berm material exchange has been developed by [7]. Efforts have focused on improving the model to better reproduce the overall shift in material between the subaerial and subaqueous portions of the profile by taking into account the long-term evolution of multi-bar systems and the response of offshore mounds placed in the outer part of the nearshore zone to act as active or feeder bars (for beach nourishment purposes, [67]). The model is based on simplifications of the governing processes, where bar volume evolution determines the transport direction, i.e., bar growth implies offshore sediment transport and bar decay corresponds to onshore sediment transport. The presented two-bar model, rather than resolve the fine details of the profile response (or bar shape), relies on a simple approach to compute volume changes distributed between the two bars, with the assumption that larger waves result in more material in the bars compared to smaller waves (quantified based on data). A transfer of material from offshore deposits (longshore bars) towards shallower portions was incorporated, once an exchange of material continually takes place between these areas, depending on change in the nearshore wave conditions. As opposed to the deeper bars, which are exposed to wave breaking only during large storms, the surf zone experiences breaking waves during most of the year [67]. Thus, a rapid response rate is expected for this region, i.e., a considerable sensitivity to changes in the nearshore, affecting also the shoreline movement. The CS-model does not resolve the necessary hydrodynamic quantities to predict cross-shore sediment transport rates in the surf zone (as the SBEACH model does for example). Instead, from a regional perspective, the total volume corresponding to the subaqueous portion of the profiles is described as a function of the bar volume variation computed in relation to its equilibrium value [7].

4.2. Design Coastal Structures: XD-Coast

According to [71], waves, tides and currents represent the actions over coastal structures during their life time. However, the geotechnical/geological constitution of the bottoms and their dynamics, as well as the construction techniques and equipment, are aspects that can critically constrain the design in terms of its geometry and structural components. Nevertheless, the greatest uncertainty in the pre-design of the structures lies in the quantification of the actions, characterized essentially by the incident wave height, where the combination of knowledge and rules with common sense is required. As the recommended value for the design wave height is a complex subject, whose considerations vary for each specific case, it is convenient to study the solution sensitivity to its variation [72].

There are several methods to pre-design coastal structures, which basically consist of different formulations for defining the blocks weight of the resistant layer of a structure, which should resist to the incident wave actions. The formulations vary depending on whether the structures are non-overtopped, overtopped or submerged. Adding to the blocks weight, other aspects of the structures cross-section need to be defined (crest width, thickness of the layers, revetment slope, etc.) and different materials can be adopted. Thus, specific manuals are indispensable in the study and design of coastal structures, being highlighted below the main publications to be considered [72]:

• Shore Protection Manual [73]. It was the first publication of the United States Army Corps of Engineers, in 1974, being updated in 1984. This document contains the fundamental principles of coastal engineering;
• Coastal Engineering Manual (CEM). Following the Shore Protection Manual, CEM presents six parts, divided by chapters, being the Chapter 5 of part VI (Fundamentals of Design, [74]) direct to the pre-design of coastal structures;
• The Rock Manual [75]. It is a complete manual about the main concepts applied in coastal engineering. Chapters 5 (Physical Processes and Design Tools) and 6 (Design of Marine Structures), respectively [76,77], are directly related with the pre-design of coastal structures.
• Maritime Structures—Part 7: Guide to design and construction of breakwaters, of British Standard Institution [78]. This document is a practical guide of coastal structures design, being similar to a “Eurocode for Coastal Engineering”.

Information regarding the documents that define the design rules and practices in some countries was gathered by [79]. According to the author, the United States follows the standards set in the CEM and Rock Manual. In Europe, the UK stands out along the lines defined by the British Standard Institution, Spain follows the standards of the Maritime Works Recommendations (ROM) and Germany follows the rules set by the Committee for Waterfront Structures Harbors and Waterways. Other documents such as [80,81,82,83], etc., can assist the design phase of coastal works.

According to [72], the knowledge of the parameters involved in the empirical formulations is fundamental. The development of automatic tools that allow the implementation of different solutions in order to obtain optimized results, quickly and expeditiously is demanded. Some existing numerical tools can be referred: XD-Coast; BREAKWAT; CRESS; CLI. According to [84], BREAKWAT is a coastal structures design tool, developed by WL-Delft Hydraulics, in 1980. Reference [85] refers that this tool considers several different formulae for the design of different types of structures (non-overtopped, overtopped, submerged, with a berm, vertical, etc.). The coastal and river engineering support system (CRESS) model consists of a set of subroutines, each containing a formulation or group of formulas, of important application in coastal and river engineering [86]. The model is based on the concepts and formulations described in Rock Manual [75] and it is available online. Concrete layer innovations (CLI) is a company dedicated to the development and manufacture of precast concrete blocks for application in the rough layer of coastal structures. In order to assist the preliminary calculations of a coastal works project [87], CLI makes available on its website a block pre-design tool, based on the Hudson formula [88].

The numerical pre-design tool XD-Coast (Xpress design of coastal structures) was developed by [89], allowing the calculation of armor layer blocks unit weight, considering different formulations and types of structures. The main characteristics of the cross-section are also defined, in function of the armor layer blocks unit weight [90]. This tool considers the load represented by the wave height and allows evaluating three different formulations for calculations related to non-overtopped structures: [88,91] for rocks, and [92,93] for tetrapod. For low-crested and submerged structures, the model has one formulation available: [94] for rocks. Once the cross-section is defined, knowing the bathymetry and topography at the structures location, the total dimension and the volume of each structure layer and type of material is calculated (Figure 6).

Coastal intervention costs estimate (construction and maintenance) are based on structures dimensions and required material. In the cost–benefit tool, monetary values are assigned to the materials volumes and structures maintenance requirements [72].

5. Costs and Benefits

Costs and benefits analysis are fundamental to support the decisions on medium to long-term management and planning strategies. According to [72], over the last decades the focus of studies moved from physical effectiveness to a more comprehensive management of coastal zones, evaluating adaptation measures with economic tools such as cost-effectiveness, cost–benefit and efficiency analyses [95]. Moreover, when discussing climate related threats with decision-makers, cost–benefit analyses that support decisions are often demanded [96]. Cost–benefit studies provide insight in what adaptation measures/strategies provide largest net benefits, assessing costs and benefits of engineering measures [96,97,98,99,100,101,102,103,104,105]. Coastal zone managers should rely on cost–benefit analyses when defining protection, adaptation and/or retreat strategies [106]. In order to deal with the complexity and uncertainty of the coastal erosion problems, action-plans require well-developed methodologies and tools, including participatory approaches, to provide efficient and effective means of supporting decision-making [107,108,109]. However, traditionally, coastal erosion was assessed using engineering approaches, such that the physical effectiveness of adaptation measures was assessed without taking into consideration associated cost and benefit [110]. Coastal interventions to mitigate erosion need to be thoroughly evaluated, as they represent an interference with the coastal environment and, hence, lead to multiple, divergent and location specific impacts [39], and imply large investment, as well as maintenance costs.

Therefore, a methodology to analyze and discuss the most adequate adaptation strategies to coastal erosion in combination with socio-environmental-economic expertise was presented by [72], considering the costs and benefits related to each intervention, by applying a well-defined and sequential cost–benefit approach (COAST—coastal optimization assessment tool). The goal of this methodology is to support decision-making for planning and coastal management with sustainable coastal interventions, by encompassing the assessment of the shoreline evolution impacts (with a shoreline evolution model, preferentially LTC), and the design of artificial nourishment or coastal structures (preferentially applying the CS-model and/or XD-Coast, previously described), allowing the final costs and benefits analysis.

COAST allows identifying and quantifying all the positive factors (benefits) and negative factors (costs) related to a certain intervention scenario. The total costs associated with a coastal defense intervention encompass not only construction costs but also periodic maintenance costs, and both depend on the type of intervention to be carried out and vary depending on various factors (materials, cross section, location, etc.). It should be noticed that in addition to the costs related to the structural intervention, costs resulting from the social, cultural and environmental impact of the intervention, as well as any damage to neighboring infrastructure must be taken into account [72]. The quantification of benefits is determined on the basis of the areas gained and/or lost over the time period under analysis and vary depending on the land use value (which must take into account environmental, social, cultural, historical, etc. aspects). The benefit transfer methodology allows the qualitative or quantitative adaptation of environmental resources to economic values, as exemplified by the works of [99,111,112]. The only measure that allows evaluating benefits and costs in the same unit is the currency unit. It is important to note that for different periods it is necessary to update the economic values for a reference year [113].

Generally, the verification of the economic sustainability of each coastal intervention is made from the accumulated net flows of benefits and costs [72]. Thus, for a given time frame, the economic viability of each scenario under analysis is assessed from the balance between total benefits and total costs. The value associated with costs (construction and maintenance) and benefits is a matter to be given some attention as it depends on many factors, varying over time and location. Given that coastal interventions generally lead to large investments, in addition to verifying the economic sustainability of each intervention, cost–benefit analysis leading to optimized solutions is also vital. There are no known numerical tools for cost–benefit analysis of coastal defense interventions, existing only theoretical methodologies based on studies developed by several authors. However, the dynamic and interactive vulnerability assessment (DIVA) tool, which is a part of the dynamic and interactive assessment of national, regional and global vulnerability of coastal zones to climate change and sea-level rise, DINAS-COAST project allows us to develop economic and environmental studies applied to coastal areas, helping to choose adaptation strategies based on different economic scenarios [114,115]. This methodology has already been applied in studies related to climate change, namely by [96].

The cost–benefit analysis performed with COAST allows us to estimate the net present value of different intervention scenarios for coastal erosion mitigation, and the direct comparison of results between various simulated scenarios, also allowing the calculation of the benefit–cost ratio to assess the economic viability of each solution. At the same time, the main physical results (accretion and erosion areas) can be seen as a result of the analysis (Figure 7).

Different coastal intervention alternatives may be associated with different levels of functional effectiveness, structural robustness, sedimentary and morphological impacts on the environment, landscape impacts, construction difficulties, maintenance needs and cost [39]. The cost assessment of a coastal structure involves several aspects, not only related to the type of intervention, but also, with the location, function, economic conjecture, material availability, the intervention dimension, etc. The dimensions and depth at which the works will be deployed can lead to more difficulties, and thus increased costs. Costs also depend on the materials used, the frequency of maintenance and the degree of exposure to which the works are subject. It should also be noted that in a cost assessment, the costs can be divided into direct costs, directly related to the implementation of the intervention, and indirect, which may appear across the application of the chosen solution [72]. In the COAST tool, the cost estimate to be considered in the cost–benefit analysis encompasses the direct and indirect costs of construction and maintenance over the analyzed period. It is emphasized that when quantifying costs, the user must take into account economic, social, cultural, environmental, etc. aspects at the same time and should proceed with caution due to the high uncertainty associated with their estimation. According to [72], in any application, the user should collect information specific to the intervention site and should perform a sensitive analysis to the results.

The benefits of a coastal defense intervention correspond to areas of territory (gained or lost by the effect of the intervention) affected by its economic value. The area gained, or not lost, represents the area that is recovered due to the adopted solution. For cost–benefit analysis, the areas resulting from each simulation scenario are converted into a monetary value, thus enabling a comparison with the costs associated with coastal defense interventions. The attribution of economic value to the territory must take into account the various ecosystems that exist and the benefits they can bring over time, combining geomorphological, ecological and human occupation characteristics of the territory [72]. It is also important to mention that, when assigning a value to the territory, in addition to quantifying the benefits that both the territory and the ecosystems may represent, it is important to analyze the occupation evolution over time. This is because it is often possible to predict either the value increase or decrease of a given area over a time horizon (e.g., unpopulated neighborhoods that may give rise to housing/tourist facilities, etc.). Similar to this, temporal defenses or soft interventions can also represent an additional value to the territory during part of the time horizon of analysis. It is also highlight that the attribution of values to the territory is a key issue in the results that may be obtained [72], and should be sustained with information gathered from the city councils, insurance companies, real estate agencies, etc.

Some generic applications of COAST were presented by [72,116,117], considering hypothetical values to discuss different scenarios of interventions to mitigate coastal erosion. At the present, COAST is being considered in a real situation to evaluate costs and benefits of sand by-passing systems in two harbors of the Portuguese Northwest coast, and to discuss coastal erosion mitigation strategies at the Ovar municipality (Portuguese Northwest coast), in the aim of the INCCA (Integrated Coastal Climate Change Adaptation for Resilient Communities) project, started in February 2020. Those studies highlight the importance of COAST as a cost-benefit assessment tool.

6. Conclusions

A brief review of coastal modeling tools was presented, supporting a discussion on general coastal management and planning procedures. Following the numerical models review, a sequence of useful tools brought in COMASO was presented to guide coastal engineers and managers on the decision-making process. It is considered important to easily map coastal erosion vulnerabilities and risk, and related climate change effects since it offers means to put preventive measures in place. A method to identify and highlight the priorities of intervention in a simple and low data demanding process is highly valuable in the coastal management process. Overall, CERA corresponds to a coastal erosion risk assessment methodology for short to medium-term, based on current indicators. This methodology is flexible enough to be applicable to a wide range of coastal environments and scales, with variable accuracy, depending on the input data. Moreover, the methodology has an accessible process that avoids numerical modeling and can be replicated by interested users and stakeholders without major resources required.

To proceed with an adequate management at the vulnerable and risk areas, it is considered important to forecast the shoreline and profile evolution under alternative scenarios of wave climate and climate change effects and intervention options. The one-line theory models combined with the cross-shore numerical models can help to discuss different intervention scenarios, allowing to test different engineering solutions and evaluate their performance as an attempt to improve the physical response of the shoreline and the beach profile. It is considered that LTC model can continue to be developed and may integrate complementary tools, which together with the design of interventions and the analysis of its costs and benefits will facilitate the identification of adequate coastal erosion mitigation strategies, helping on planning and management of the coastal zones. Profile models operating at long-term, such CS-model, present great potential to be merged with longshore models, since it takes into account transport processes that act over compatible time scales, e.g., dune recovery, but also short-term processes such as the impact of individual storms, which may cause abrupt changes in the system with long-lasting consequences for the beach morphology.

The CS-model allows simulations detailing the gradual evolution of distinct fill design schemes in response to changes in the forcing conditions, determining the time scale and redistribution of the fill material. Fill design schemes may be discussed considering the purpose for which the project is designed. Coastal structures cross-section may be discussed with XD-Coast. When knowing the bathymetry and topography at the structures location, the total dimension and the volume of each structure layer and type of material is calculated with this tool. Coastal intervention costs estimate (construction and maintenance) are based on structures dimensions and required material, which is fundamental for an adequate planning of the interventions. In the cost–benefit tool, monetary values are assigned to the materials volumes and structures maintenance requirements.

Finally, costs and benefits analysis are fundamental to support the decisions on medium to long-term management and planning strategies. It was identified that over the last decades the focus of studies moved from physical effectiveness to a more comprehensive management of the coastal zones, evaluating adaptation measures with economic tools. The main objective of COAST tool is the analysis of different scenarios and the optimization of solutions considering simultaneously physical and economical aspects, since there are numerous possibilities and considerations that can be taken into account in the design of coastal defense interventions to mitigate the problem of coastal erosion.

Finally, it is considered that COMASO tools can help giving answers to the major problems of the coastal planning and management entities, integrating transversal knowledge in risk assessment, physical processes, engineering and economic evaluations. The integrated coastal zone management needs these tools to create resilient and sustainable coastal zones, mitigating erosion and climate change effects.