An Analytical Model for Rock Cutting with a Chisel Pick of the Cutter Suction Dredger
Abstract
:1. Introduction
2. A Brief Review of the Models for Rock Cutting with Chisel Picks
2.1. Evans’ Tensile Breakage Model
2.2. Nishimatsu’s Shear Breakage Model
2.3. Semi-Empirical Models
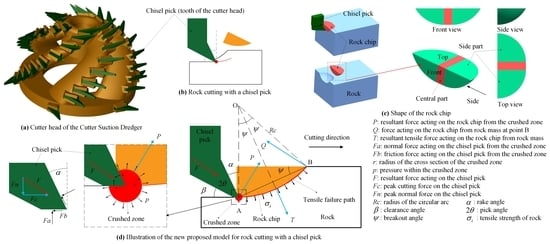
3. Establishment of the CEIT Model
3.1. Conception of the CEIT Model
3.2. Mechanical Model and Mathematical Formula of the CEIT Model
3.3. An Approximate Value of the Breakout Angle in the CEIT Model
4. Validation of the CEIT Model
4.1. Validity of the CEIT Model in Capturing the Effects of the Cutting Parameters
4.2. Comparison of the CEIT Model and the Existing Theoretical Models
5. Discussions
5.1. Sidewall Effect in the CEIT Model
5.2. Advantages and Limitations of the CEIT Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ab Adzis, A.H.; Abdul-Rani, A.M.; Yi, K.Y.; Maulianda, B.T.; Rao, T.V.V.L.N. Effect of back rake angle and shape on wear rate of pdc cutter in hard formation. In Proceedings of the 6th International Conference on Production, Energy and Reliability 2018: World Engineering Science & Technology Congress, Kuala Lumpur, Malaysia, 13–14 August 2018; Volume 2035. [Google Scholar]
- Rostamsowlat, I.; Akbari, B.; Evans, B. Analysis of rock cutting process with a blunt pdc cutter under different wear flat inclination angles. J. Pet. Sci. Eng. 2018, 171, 771–783. [Google Scholar] [CrossRef]
- Akbari, B.; Miska, S. The effects of chamfer and back rake angle on pdc cutters friction. J. Nat. Gas Sci. Eng. 2016, 35, 347–353. [Google Scholar] [CrossRef]
- Rostamsowlat, I.; Richard, T.; Evans, B. An experimental study of the effect of back rake angle in rock cutting. Int. J. Rock Mech. Min. Sci. 2018, 107, 224–232. [Google Scholar] [CrossRef] [Green Version]
- Rostamsowlat, I.; Richard, T.; Evans, B. Experimental investigation on the effect of wear flat inclination on the cutting response of a blunt tool in rock cutting. Acta Geotech. 2019, 14, 519–534. [Google Scholar] [CrossRef]
- Doshvarpassand, S.; Richard, T.; Mostofi, M. Effect of groove geometry and cutting edge in rock cutting. J. Pet. Sci. Eng. 2017, 151, 1–12. [Google Scholar] [CrossRef]
- Che, D.; Han, P.; Guo, P.; Ehmann, K. Issues in polycrystalline diamond compact cutter-rock interaction from a metal machining point of view-part I: Temperature, stresses, and forces. J. Manuf. Sci. Eng. Trans. ASME 2012, 134, 064001. [Google Scholar] [CrossRef]
- Che, D.; Han, P.; Guo, P.; Ehmann, K. Issues in polycrystalline diamond compact cutter-rock interaction from a metal machining point of view-part II: Bit performance and rock cutting mechanics. J. Manuf. Sci. Eng. Trans. ASME 2012, 134, 064002. [Google Scholar] [CrossRef]
- Detournay, E.; Richard, T.; Shepherd, M. Drilling response of drag bits: Theory and experiment. Int. J. Rock Mech. Min. Sci. 2008, 45, 1347–1360. [Google Scholar] [CrossRef]
- Li, X.B.; Summers, D.A.; Rupert, G.; Santi, P. Experimental investigation on the breakage of hard rock by the pdc cutters with combined action modes. Tunn. Undergr. Space Technol. 2001, 16, 107–114. [Google Scholar] [CrossRef]
- Menezes, P.L.; Lovell, M.R.; Avdeev, I.V.; Higgs, C.F., III. Studies on the formation of discontinuous rock fragments during cutting operation. Int. J. Rock Mech. Min. Sci. 2014, 71, 131–142. [Google Scholar] [CrossRef] [Green Version]
- Richard, T.; Dagrain, F.; Poyol, E.; Detournay, E. Rock strength determination from scratch tests. Eng. Geol. 2012, 147, 91–100. [Google Scholar] [CrossRef]
- Detournay, E.; Defourny, P. A phenomenological model for the drilling action of drag bits. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1992, 29, 13–23. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, X.; Jing, J. The analysis of ductile-brittle failure mode transition in rock cutting. J. Pet. Sci. Eng. 2018, 163, 311–319. [Google Scholar] [CrossRef]
- Richard, T.; Coudyzer, C.; Desmette, S. Influence of groove geometry and cutter inclination in rock cutting. In Proceedings of the 44th US Rock Mechanics Symposium—5th US/Canada Rock Mechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010. [Google Scholar]
- Richard, T.; Detournay, E.; Drescher, A.; Nicodeme, P.; Fourmaintraux, D. The scratch test as a means to measure strength of sedimentary rocks. In SPE/ISRM Rock Mechanics in Petroleum Engineering; Society of Petroleum Engineers: Trondheim, Norway, 1998; pp. 1–8. [Google Scholar]
- Miedema, S. The Delft Sand, Clay & Rock Cutting Model, 3rd ed.; IOS Press: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Zhou, Y.; Lin, J.-S. On the critical failure mode transition depth for rock cutting. Int. J. Rock Mech. Min. Sci. 2013, 62, 131–137. [Google Scholar] [CrossRef]
- He, X.; Xu, C.; Peng, K.; Huang, G. On the critical failure mode transition depth for rock cutting with different back rake angles. Tunn. Undergr. Space Technol. 2017, 63, 95–105. [Google Scholar] [CrossRef]
- Evans, I. A theory on the basic mechanics of coal ploughing. In Mining Research; Clark, G.B., Ed.; Elsevier: Amsterdam, The Netherlands, 1962; pp. 761–798. [Google Scholar]
- Evans, I. The force required to cut coal with blunt wedges. Int. J. Rock Mech. Min. Sci. 1965, 2, 1–2. [Google Scholar] [CrossRef]
- Evans, I. A theory of the cutting force for point attack-picks. Int. J. Min. Eng. 1984, 2, 9. [Google Scholar] [CrossRef]
- Goktan, R. Prediction of Drag Bit Cutting Force in Hard Rocks. In Proceedings of the 3rd International Symposium on Mine Mechanization and Automation, Golden, Colorado, 1 June 1995; pp. 10–31. [Google Scholar]
- Goktan, R.M. A Suggested Improvement on Evans’ Cutting Theory for Conical Bits. In Proceedings of the 4th International Symposium on Mine Mechanization and Automation, Brisbane, Australia, 1 July 1997. [Google Scholar]
- Goktan, R.M.; Gunes, N. A semi-empirical approach to cutting force prediction for point-attack picks. J. S. Afr. Inst. Min. Metall. 2005, 105, 257–263. [Google Scholar]
- Nishimatsu, Y. The mechanics of rock cutting. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1972, 9, 261–270. [Google Scholar] [CrossRef]
- Allington, A.V. The Machining of Rock Materials; University of Newcastle upon Tyne: Newcastle, UK, 1969. [Google Scholar]
- Bilgin, N. Investigations into the Mechanical Cutting Characteristics of Some Medium and High Strength Rocks; University of Newcastle Upon Tyne: Newcastle, UK, 1977. [Google Scholar]
- Spagnoli, G.; Bosco, C.; Oreste, P. The influence of the rake angle on the excavation energy in a sandstone. Géotechnique Lett. 2017, 7, 30–35. [Google Scholar] [CrossRef]
- Bilgin, N.; Demircin, M.A.; Copur, H.; Balci, C.; Tuncdemir, H.; Akcin, N. Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results. Int. J. Rock Mech. Min. Sci. 2006, 43, 139–156. [Google Scholar] [CrossRef]
- Yasar, S.; Yilmaz, A. Drag pick cutting tests: A comparison between experimental and theoretical results. J. Rock Mech. Geotech. Eng. 2018, 10, 893–906. [Google Scholar] [CrossRef]
- Yilmaz, N.G.; Yurdakul, M.; Goktan, R.M. Prediction of radial bit cutting force in high-strength rocks using multiple linear regression analysis. Int. J. Rock Mech. Min. Sci. 2007, 44, 962–970. [Google Scholar] [CrossRef]
- Ouyang, Y. Studies on Cutting Mechanism of Pick Cutters for Rock Dredging; Shanghai Jiao Tong University: Shanghai, China, 2013. [Google Scholar]
- Su, O. Numerical modeling of cuttability and shear behavior of chisel picks. Rock Mech. Rock Eng. 2019, 52, 1803–1817. [Google Scholar] [CrossRef]
- Yasar, S. A general semi-theoretical model for conical picks. Rock Mech. Rock Eng. 2020, 53, 2557–2579. [Google Scholar] [CrossRef]
- Dagrain, F.; Detournay, E.; Richard, T. Influence of the Cutter Geometry in Rock Cutting: An Experimental Approach; University of Minnesota: Minneapolis, MN, USA, 2001. [Google Scholar]
- Ghoshouni, M.; Richard, T. Effect of the back rake angle and groove geometry in rock cutting. In ISRM International Symposium—5th Asian Rock Mechanics Symposium; International Society for Rock Mechanics and Rock Engineering: Tehran, Iran, 2008; p. 10. [Google Scholar]
- Roxborough, F.F.; King, P.; Pedroncelli, E.J. Tests on the cutting performance of a continuous miner. J. S. Afr. Inst. Min. Metall. 1981, 81, 9–25. [Google Scholar]
- Rutten, T.; Chen, X.; Liu, G.; Hong, G.; Miedema, S. Experimental study on rock cutting with a pickpoint. In Proceedings of the CEDA Dredging Days 2019, Rotterdam, The Netherlands, 8 November 2019. [Google Scholar]
- Chen, X.; Miedema, S.; van Rhee, C. Numerical methods for modeling the rock cutting process in deep sea mining. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Chen, X.; Miedema, S.A.; van Rhee, C. Numerical modeling of excavation process in dredging engineering. Procedia Eng. 2015, 102, 804–814. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.H.; Liu, S.Y.; Tang, P. Coal fragment size model in cutting process. Powder Technol. 2015, 272, 282–289. [Google Scholar] [CrossRef]
- Shao, W.; Li, X.; Sun, Y.; Huang, H.; Tang, J. An experimental study of temperature at the tip of point-attack pick during rock cutting process. Int. J. Rock Mech. Min. Sci. 2018, 107, 39–47. [Google Scholar] [CrossRef]
- Mishnaevsky, L.L. Investigation of the cutting of brittle materials. Int. J. Mach. Tools Manuf. 1994, 34, 499–505. [Google Scholar] [CrossRef]
- Xue, J.; Xia, Y.; Ji, Z.; Zhou, X. Soft rock cutting mechanics model of tbm cutter and experimental research. In International Conference on Intelligent Robotics and Applications; Xie, M., Xiong, Y., Xiong, C., Liu, H., Hu, Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5928, pp. 383–391. [Google Scholar]
- Menezes, P.L. Influence of friction and rake angle on the formation of built-up edge during the rock cutting process. Int. J. Rock Mech. Min. Sci. 2016, 88, 175–182. [Google Scholar] [CrossRef]
- Yasar, S.; Yilmaz, A.O. Rock cutting tests with a simple-shaped chisel pick to provide some useful data. Rock Mech. Rock Eng. 2017, 50, 3261–3269. [Google Scholar] [CrossRef]
- Ouyang, Y.; Yang, Q.; Ma, J.; Qiu, Y. Effects of rake angle on linear rock cutting with chisel picks. J. Shanghai Jiaotong Univ. 2018, 52, 1422–1428. [Google Scholar]
- Copur, H.; Bilgin, N.; Tuncdemir, H.; Balci, C. A set of indices based on indentation tests for assessment of rock cutting performance and rock properties. J. S. Afr. Inst. Min. Metall. 2003, 103, 589–599. [Google Scholar]
- Kim, E.; Rostami, J.; Swope, C. Full scale linear cutting experiment to examine conical bit rotation. J. Min. Sci. 2012, 48, 882–895. [Google Scholar] [CrossRef]
- Wang, X.; Su, O.; Wang, Q.-F.; Liang, Y.-P. Effect of cutting depth and line spacing on the cuttability behavior of sandstones by conical picks. Arab. J. Geosci. 2017, 10, 525. [Google Scholar] [CrossRef]
- Gharsallaoui, H.; Jafari, M.; Holeyman, A. Cavity expansion in rock masses obeying the “hoek-brown” failure criterion. Rock Mech. Rock Eng. 2020, 53, 927–941. [Google Scholar] [CrossRef]
- Alehossein, H.; Detournay, E.; Huang, H. An analytical model for the indentation of rocks by blunt tools. Rock Mech. Rock Eng. 2000, 33, 267–284. [Google Scholar] [CrossRef]
- Huang, H.; Damjanac, B.; Detournay, E. Normal wedge indentation in rocks with lateral confinement. Rock Mech. Rock Eng. 1998, 31, 81–94. [Google Scholar] [CrossRef]
- Forrestal, M.J.; Tzou, D.Y. A spherical cavity-expansion penetration model for concrete targets. Int. J. Solids Struct. 1997, 34, 4127–4146. [Google Scholar] [CrossRef]
- Luk, V.K.; Forrestal, M.J.; Amos, D.E. Dynamic spherical cavity expansion of strain-hardening materials. Trans. ASME J. Appl. Mech. 1991, 58, 1–6. [Google Scholar] [CrossRef]
- Chen, L.H.; Labuz, J.F. Indentation of rock by wedge-shaped tools. Int. J. Rock Mech. Min. Sci. 2006, 43, 1023–1033. [Google Scholar] [CrossRef]
- Wang, X.; Su, O. Specific energy analysis of rock cutting based on fracture mechanics: A case study using a conical pick on sandstone. Eng. Fract. Mech. 2019, 213, 197–205. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Ge, S.; Malekian, R.; Li, Z. A theoretical model for estimating the peak cutting force of conical picks. Exp. Mech. 2018, 58, 709–720. [Google Scholar] [CrossRef]
- Gao, K.; Du, C.; Jiang, H.; Liu, S. A theoretical model for predicting the peak cutting force of conical picks. Frat. Integrita Strutt. 2014, 8, 43–52. [Google Scholar]
- Bao, R.; Zhang, L.; Yao, Q.; Lunn, J. Estimating the peak indentation force of the edge chipping of rocks using single point-attack pick. Rock Mech. Rock Eng. 2011, 44, 339–347. [Google Scholar] [CrossRef]
- Ouyang, Y.; Yang, Q. Numerical simulation of rock cutting in 3d with sph method and estimation of cutting force. J. Shanghai Jiaotong Univ. 2016, 50, 84–90. [Google Scholar]
- Roxborough, F. Cutting rock with picks. Min. Eng. 1973, 132, 445–455. [Google Scholar]
- Dogruoz, C.; Bolukbasi, N.; Rostami, J.; Acar, C. An experimental study of cutting performances of worn picks. Rock Mech. Rock Eng. 2016, 49, 213–224. [Google Scholar] [CrossRef]
















| Models | Establishments | Parameters | Advantages | Disadvantages |
|---|---|---|---|---|
| Evans | theoretical model in 2D based on tensile fracture | , , w, d, | strong adaptability and theoretical basis, very easy to apply, | underestimate cutting force, 2D model |
| Nishimatsu | theoretical model in 2D based on shear fracture | , , n, w, d, | strong adaptability and theoretical basis, moderate easy to apply | prediction accuracy depends on and n, 2D model |
| Goktan & Ouyang | empirical model in 3D based on experimental results | , , w, d, , | accurate estimation for some kinds of hard rocks | lack of theoretical support, uncertain adaptability |
| Rock Samples | ||||||
|---|---|---|---|---|---|---|
| /MPa | /MPa | /MPa | /deg. | /deg. | /deg. | |
| Anhydrite a | 112.91 | 5.47 | 12.5 | 43 | 36.4 | 21.4 |
| Limestone a | 127.25 | 7.45 | 20 | 37 | 32.3 | 23.4 |
| Granite a | 179.10 | 10.77 | 30 | 42 | 21.5 | 14.9 |
| Greywacke a | 183.86 | 16.45 | 34 | 33 | 23.6 | 11.3 |
| Anhydrite 2 b | 100 | 6.7 | 12.5 | 43 | 36.4 | 21.4 |
| Limestone 2 b | 200 | 7.8 | 20 | 37 | 32.3 | 23.4 |
| Models | Formulas | RMSE | Bias | R2 |
|---|---|---|---|---|
| Evans | Formula (6) | 7.19 | −5.43 | 0.56 |
| Nishimatsu | Formula (12) | 9.53 | −7.97 | 0.50 |
| CEIT | Formula (24) | 4.56 | −2.16 | 0.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, Y.; Yang, Q.; Chen, X.; Xu, Y. An Analytical Model for Rock Cutting with a Chisel Pick of the Cutter Suction Dredger. J. Mar. Sci. Eng. 2020, 8, 806. https://doi.org/10.3390/jmse8100806
Ouyang Y, Yang Q, Chen X, Xu Y. An Analytical Model for Rock Cutting with a Chisel Pick of the Cutter Suction Dredger. Journal of Marine Science and Engineering. 2020; 8(10):806. https://doi.org/10.3390/jmse8100806
Chicago/Turabian StyleOuyang, Yiping, Qi Yang, Xinquan Chen, and Yongfu Xu. 2020. "An Analytical Model for Rock Cutting with a Chisel Pick of the Cutter Suction Dredger" Journal of Marine Science and Engineering 8, no. 10: 806. https://doi.org/10.3390/jmse8100806
APA StyleOuyang, Y., Yang, Q., Chen, X., & Xu, Y. (2020). An Analytical Model for Rock Cutting with a Chisel Pick of the Cutter Suction Dredger. Journal of Marine Science and Engineering, 8(10), 806. https://doi.org/10.3390/jmse8100806