Significance of Arrhenius Activation Energy and Binary Chemical Reaction in Mixed Convection Flow of Nanofluid Due to a Rotating Disk
Abstract
:1. Introduction
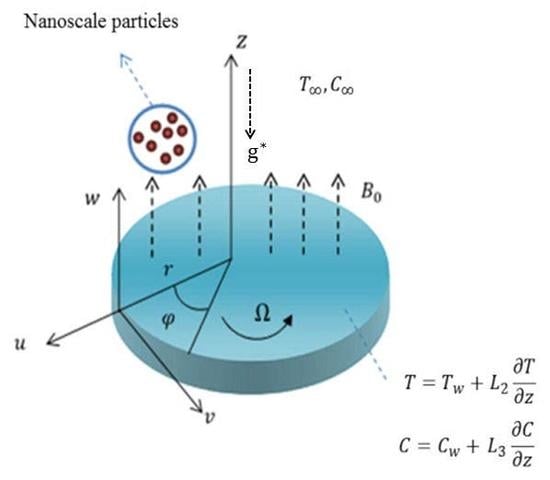
2. Problem Description
3. Solution Methodology
4. Graphical Results and Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| w | velocity components | z | coordinate axes |
| electrical conductivity | magnetic field strength | ||
| dynamic viscosity | density of base fluid | ||
| thermal expansion coefficient | concentration expansion coefficient | ||
| kinematic viscosity | acceleration due to gravity | ||
| velocity slip coefficient | temperature slip coefficient | ||
| concentration slip coefficient | constant angular velocity | ||
| T | temperature | C | concentration |
| wall temperature | wall concentration | ||
| ambient fluid temperature | ambient fluid concentration | ||
| thermal diffusivity | k | thermal conductivity | |
| effective heat capacity of nanoparticles | heat capacity of fluid | ||
| Brownian diffusion coefficient | thermophoretic diffusion coefficient | ||
| activation energy | n | fitted rate constant | |
| reaction rate | Boltzmann constant | ||
| similarity variable | g | dimensionless velocities | |
| dimensionless temperature | dimensionless concentration | ||
| Schmidt number | Hartman number | ||
| thermal buoyancy number | Pr | Prandtl number | |
| Brownian motion parameter | thermophoresis parameter | ||
| concentration buoyancy number | velocity slip parameter | ||
| thermal slip parameter | concentration slip parameter | ||
| E | dimensionless activation energy | temperature difference parameter | |
| skin friction coefficients | local rotational Reynolds number | ||
| Nusselt number | Sherwood number |
References
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids With Nanoparticles; FED 231/MD; Argonne National Lab.: Lemont, IL, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluid. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar]
- Abu-Nada, E.; Oztop, H.F. Effects of inclination angle on natural convection in enclosures filled with Cu-water nanofluid. Int. J. Heat Fluid Flow 2009, 30, 669–678. [Google Scholar]
- Mansur, S.; Ishak, A. Three-dimensional flow and heat transfer of a nanofluid past a permeable stretching sheet with a convective boundary condition. AIP Conf. Proc. 2014, 1614, 906–912. [Google Scholar]
- Hayat, T.; Muhammad, T.; Alsaedi, A.; Alhuthali, M.S. Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. J. Magn. Magn. Mater. 2015, 385, 222–229. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J.; Gorla, R.S.R. Nonlinear radiative heat transfer in MHD three-dimensional flow of water based nanofluid over a non-linearly stretching sheet with convective boundary condition. J. Niger. Math. Soc. 2016, 35, 178–198. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. On magnetohydrodynamic three-dimensional flow of nanofluid over a convectively heated nonlinear stretching surface. Int. J. Heat Mass Transf. 2016, 100, 566–572. [Google Scholar]
- Muhammad, T.; Alsaedi, A.; Shehzad, S.A.; Hayat, T. A revised model for Darcy-Forchheimer flow of Maxwell nanofluid subject to convective boundary condition. Chin. J. Phys. 2017, 55, 963–976. [Google Scholar]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A. On magnetohydrodynamic flow of nanofluid due to a rotating disk with slip effect: A numerical study. Comp. Methods Appl. Mech. Eng. 2017, 315, 467–477. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Kataria, H.R.; Mittal, A.S. Radiation effects on heat transfer of three dimensional nanofluid flow considering thermal interfacial resistance and micro mixing in suspensions. Chin. J. Phys. 2017, 55, 2254–2272. [Google Scholar] [CrossRef]
- Muhammad, T.; Alsaedi, A.; Hayat, T.; Shehzad, S.A. A revised model for Darcy-Forchheimer three-dimensional flow of nanofluid subject to convective boundary condition. Results Phys. 2017, 7, 2791–2797. [Google Scholar] [CrossRef]
- Hayat, T.; Sajjad, R.; Muhammad, T.; Alsaedi, A.; Ellahi, R. On MHD nonlinear stretching flow of Powell-Eyring nanomaterial. Results Phys. 2017, 7, 535–543. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Study of shiny film coating on multi-fluid flows of a rotating disk suspended with nano-sized silver and gold particles: A comparative analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef] [Green Version]
- Selimefendigil, F.; Oztop, H.F. Mixed convection of nanofluids in a three dimensional cavity with two adiabatic inner rotating cylinders. Int. J. Heat Mass Transf. 2018, 117, 331–343. [Google Scholar] [CrossRef]
- Muhammad, T.; Lu, D.C.; Mahanthesh, B.; Eid, M.R.; Ramzan, M.; Dar, A. Significance of Darcy-Forchheimer porous medium in nanofluid through carbon nanotubes. Commun. Theoret. Phys. 2018, 70, 361. [Google Scholar] [CrossRef]
- Suleman, M.; Ramzan, M.; Ahmad, S.; Lu, D.; Muhammad, T.; Chung, J.D. A numerical simulation of silver-water nanofluid flow with impacts of Newtonian heating and homogeneous-heterogeneous reactions past a nonlinear stretched cylinder. Symmetry 2019, 11, 295. [Google Scholar] [CrossRef] [Green Version]
- Asma, M.; Othman, W.A.M.; Muhammad, T. Numerical study for Darcy-Forchheimer flow of nanofluid due to a rotating disk with binary chemical reaction and Arrhenius activation energy. Mathematics 2019, 7, 921. [Google Scholar] [CrossRef] [Green Version]
- Asma, M.; Othman, W.A.M.; Muhammad, T.; Mallawi, F.; Wong, B.R. Numerical study formagnetohydrodynamic flow of nanofluid due to a rotating disk with binary chemical reaction and Arrhenius activation energy. Symmetry 2019, 11, 1282. [Google Scholar] [CrossRef] [Green Version]
- Saif, R.S.; Hayat, T.; Ellahi, R.; Muhammad, T.; Alsaedi, A. Darcy-Forchheimer flow of nanofluid due to a curved stretching surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 2–20. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Thermally charged MHD bi-phase flow coatings with non-Newtonian nanofluid and Hafnium particles along slippery walls. Coatings 2019, 9, 300. [Google Scholar] [CrossRef] [Green Version]
- Moradikazerouni, A.; Hajizadeh, A.; Safaei, M.R.; Afrand, M.; Yarmand, H.; Zulkifli, N.W.B.M. Assessment of thermal conductivity enhancement of nano-antifreeze containing single-walled carbon nanotubes: Optimal artificial neural network and curve-fitting. Phys. A 2019, 521, 138–145. [Google Scholar] [CrossRef]
- Asadi, A.; Aberoumand, S.; Moradikazerouni, A.; Pourfattah, F.; Żyła, G.; Estelle, P.; Mahian, O.; Wongwises, S.; Nguyen, H.M.; Arabkoohsar, A. Recent advances in preparation methods and thermophysical properties of oil-based nanofluids: A state-of-the-art review. Powder Technol. 2019, 352, 209–226. [Google Scholar] [CrossRef]
- Alsarraf, J.; Moradikazerouni, A.; Shahsavar, A.; Afrand, M.; Salehipour, H.; Tran, M.D. Hydrothermal analysis of turbulent boehmite alumina nanofluid flow with different nanoparticle shapes in a minichannel heat exchanger using two-phase mixture model. Phys. A 2019, 520, 275–288. [Google Scholar] [CrossRef]
- Vo, D.D.; Alsarraf, J.; Moradikazerouni, A.; Afrand, M.; Salehipour, H.; Qi, C. Numerical investigation of γ-AlOOH nano-fluid convection performance in a wavy channel considering various shapes of nanoadditives. Powder Technol. 2019, 345, 649–657. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Moradikazerouni, A.; Bakhtiari, R.; Asadi, A.; Afrand, M. An experimental study on stability and thermal conductivity of water/silica nanofluid: Eco-friendly production of nanoparticles. J. Clean. Prod. 2019, 206, 1089–1100. [Google Scholar] [CrossRef]
- Ma, Y.; Shahsavar, A.; Moradi, I.; Rostami, S.; Moradikazerouni, A.; Yarmand, H.; Zulkifli, N.W.B.M. Using finite volume method for simulating the natural convective heat transfer of nano-fluid flow inside an inclined enclosure with conductive walls in the presence of a constant temperature heat source. Phys. A 2019, 123035. [Google Scholar] [CrossRef]
- Von Karman, T. Uber laminare and turbulente Reibung. ZAMM Z. Angew. Math. Mech. 1921, 1, 233–252. [Google Scholar] [CrossRef] [Green Version]
- Turkyilmazoglu, M.; Senel, P. Heat and mass transfer of the flow due to a rotating rough and porous disk. Int. J. Thermal Sci. 2013, 63, 146–158. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Kavyani, N.; Abelman, S. Investigation of entropy generation in MHD and slip flow over rotating porous disk with variable properties. Int. J. Heat Mass Transf. 2014, 70, 892–917. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
- Hatami, M.; Sheikholeslami, M.; Gangi, D.D. Laminar flow and heat transfer of nanofluids between contracting and rotating disks by least square method. Powder Technol. 2014, 253, 769–779. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. On Bödewadt flow and heat transfer of nanofluids over a stretching stationary disk. J. Mol. Liq. 2015, 211, 119–125. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Numerical investigation of nanofluid spraying on an inclined rotating disk for cooling process. J. Mol. Liq. 2015, 211, 577–583. [Google Scholar] [CrossRef]
- Doh, D.H.; Muthtamilselvan, M. Thermophoretic particle deposition on magnetohydrodynamic flow of micropolar fluid due to a rotating disk. Int. J. Mech. Sci. 2017, 130, 350–359. [Google Scholar] [CrossRef]
- Aziz, A.; Alsaedi, A.; Muhammad, T.; Hayat, T. Numerical study for heat generation/absorption in flow of nanofluid by a rotating disk. Results Phys. 2018, 8, 785–792. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmad, S.; Khan, M.I.; Alsaedi, A. Modeling and analyzing flow of third grade nanofluid due to rotating stretchable disk with chemical reaction and heat source. Phys. B 2018, 537, 116–126. [Google Scholar] [CrossRef]
- Qayyum, S.; Imtiaz, M.; Alsaedi, A.; Hayat, T. Analysis of radiation in a suspension of nanoparticles and gyrotactic microorganism for rotating disk of variable thickness. Chin. J. Phys. 2018, 56, 2404–2423. [Google Scholar] [CrossRef]
- Hayat, T.; Khalid, H.; Waqas, M.; Alsaedi, A. Numerical simulation for radiative flow of nanoliquid by rotating disk with carbon nanotubes and partial slip, Comput. Methods Appl. Mech. Eng. 2018, 341, 397–408. [Google Scholar] [CrossRef]






© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, M. Significance of Arrhenius Activation Energy and Binary Chemical Reaction in Mixed Convection Flow of Nanofluid Due to a Rotating Disk. Coatings 2020, 10, 86. https://doi.org/10.3390/coatings10010086
Alghamdi M. Significance of Arrhenius Activation Energy and Binary Chemical Reaction in Mixed Convection Flow of Nanofluid Due to a Rotating Disk. Coatings. 2020; 10(1):86. https://doi.org/10.3390/coatings10010086
Chicago/Turabian StyleAlghamdi, Metib. 2020. "Significance of Arrhenius Activation Energy and Binary Chemical Reaction in Mixed Convection Flow of Nanofluid Due to a Rotating Disk" Coatings 10, no. 1: 86. https://doi.org/10.3390/coatings10010086
APA StyleAlghamdi, M. (2020). Significance of Arrhenius Activation Energy and Binary Chemical Reaction in Mixed Convection Flow of Nanofluid Due to a Rotating Disk. Coatings, 10(1), 86. https://doi.org/10.3390/coatings10010086