Electron Transfer through a Natural Oxide Layer on Real Metal Surfaces Occurring during Sliding with Polytetrafluoroethylene: Dependence on Heat of Formation of Metal Oxides
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. TriboEE and XPS
3.2. Heat of Formation of Metal Oxides with Various Oxidation Numbers
- As one moves down groups 4, 5, 6, 10, and 11 from period 4 to period 6, the highest absolute value of ΔH0 per oxygen atom in periodic groups 4, 5, and 6 does not change uniformly, as follows: TiO < ZrO2 (1/2) (Group 4); VO > NbO < Ta2O5 (Group 5); WO2 ≈ MoO2 (Group 6), while moving down groups 10 and 11 it smoothly decreases as follows: NiO > PdO > Pt3O4 (1/4) (Group 10); Cu2O > Ag2O > Au2O3 (1/3) (Group 11).
- As one progresses to the right from group 4 to group 6 in periods 4 and 5, the absolute value of ΔfH0 per oxygen atom with the same oxidation number decreases in the following order: TiO > VO (Period 4); ZrO2 (1/2) > NbO2 (1/2) > MoO2 (1/2) (Period 5); in period 6, although the oxidation number decreases from V to IV, it decreases in the following order: Ta2O5 (1/5) > WO2 (1/2) (period 6).
- Moving to the right from group 10 to group 11 in periods 4, 5, and 6, the absolute value of ΔfH0 per oxygen atom decreases in the following order: NiO > CuO (period 4); PdO > AgO (period 5); Pt3O4 (1/4) > Au2O3 (1/3) (period 6).
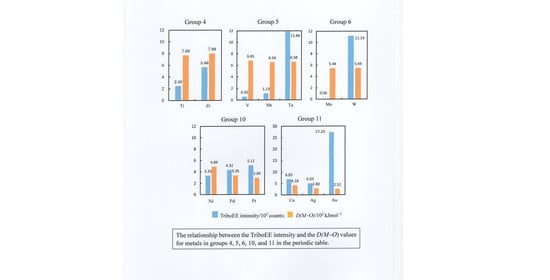
3.3. TriboEE Intensity and D(M−O)
- (a)
- 3Fe(s) + 2O2(g) → Fe3O4(s) Δf H0(Fe3O4)) = −1118.4 kJ·mol−1
- (b)
- (1/2)O2(g) → O(g) Δf H0(O(g))= +249.2 kJ·mol−1
- (c)
- (1/4) [3Fe(s) + 2O2(g)] → (1/4)[Fe3O4(s) + 1118.4 kJ·mol−1]
- (d)
- (1/2)O2(g) → O(g) − 249.2 kJ mol−1
- (e)
- (3/4)Fe(s) + O(g) →(1/4)Fe3O4(s) + [(1/4) × 1118.4] kJ·mol−1 + 249.2kJ·mol−1.
3.4. TriboEE Intensity, D(M–O), and Electrical Conductivity of Metals
3.5. D(M–O) and XPS Intensity after TriboEE Measurement
3.6. D(M–O) and XPS Intensity before TriboEE Measurement
3.7. Scheme of TriboEE by D(M–O) and O1s/Metal Core Ratio
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Masel, R.I. Adsorption I: The binding of molecules to surfaces. In Principles of Adsorption and Reaction on Solid Surfaces; John Wiley & Sons: New York, NY, USA, 1996; pp. 108–234. [Google Scholar]
- Nienhaus, H. Electronic excitations by chemical reactions on metal surfaces. Surf. Sci. Rep. 2002, 45, 1–78. [Google Scholar] [CrossRef]
- Greber, T. Charge-transfer induced particle emission in gas surface reactions. Surf. Sci. Rep. 1997, 28, 1–64. [Google Scholar] [CrossRef]
- Spikes, H.A. Triboelectrochemistry: Influence of applied electrical potentials on friction and wear of lubricated contacts. Tribol. Lett. 2020, 68, 1–27. [Google Scholar] [CrossRef]
- Ciniero, A.; Le Rouzic, J.; Baikie, I.; Reddyhoff, T. The origins of triboemission−correlating wear damage with electron emission. Wear 2017, 374–375, 113–119. [Google Scholar] [CrossRef]
- Lu, C.X.; Han, C.B.; Gu, G.Q.; Chen, J.; Yang, Z.W.; Jiang, T.; He, C.; Wang, Z.L. Temperature effect on performance of triboelectric nanogenerator. Adv. Eng. Mater. 2017, 19, 1700275–1700283. [Google Scholar] [CrossRef]
- Momose, Y.; Yamashita, Y.; Honma, M. Observation of real metal surfaces by tribostimulated electron emission and its relationship to the analyses by XPS and photoemission. Tribol. Lett. 2008, 29, 75–84. [Google Scholar] [CrossRef]
- Momose, Y.; Yamashita, Y. Triboelectron emission from metal surfaces in sliding contact with polytetrafluoroethylene: Relevance to work function and surface potential. Tribol. Int. 2012, 48, 232–236. [Google Scholar] [CrossRef]
- Momose, Y.; Kubo, K. Observation of triboelectron emission from real copper surfaces in sliding contact with polytetrafluoroethylene and polyimide. Tribol. Int. 2012, 47, 212–220. [Google Scholar] [CrossRef]
- Momose, Y.; Kosaka, S.; Sakurai, T.; Yanagisawa, M.; Nakayama, K. Photoelectric threshold of silicon wafer surfaces implanted with H, Si and Ar ions. Surf. Interface Anal. 2010, 42, 1333–1337. [Google Scholar] [CrossRef]
- Momose, Y.; Sakurai, T.; Nakayama, K. Thermal analysis of photoelectron emission (PE) and X-ray photoelectron spectroscopy (XPS) data for iron surfaces scratched in air, water, and liquid organics. Appl. Sci. 2020, 10, 2111. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Kiuchi, K.; Chinone, K.; Eguchi, M.; Momose, Y. Cyclic voltammetric study of the corrosion protection of metal surfaces by plasma-polymerized coatings. J. Adhes. Sci. Technol. 2001, 15, 371–391. [Google Scholar] [CrossRef]
- Momose, Y.; Sato, K.; Ohno, O. Electrochemical reduction of CO2 at copper electrodes and its relationship to the metal surface characteristics. Surf. Interface Anal. 2002, 34, 615–618. [Google Scholar] [CrossRef]
- Momose, Y.; Umeki, M.; Suzuki, D.; Nakayama, K. Surface electronic states and electrostatic attractive forces between metals or semiconductor and tribocharged polymers. Mater. Res. Soc. Symp Proc. 2005, 872, J21.1.1–J21.1.6. [Google Scholar] [CrossRef]
- Benziger, J.B. Thermochemical methods for reaction energetics on metal surfaces. In Metal-Surface Reaction Energetics, Theory and Applications to Heterogeneous Catalysis, Chemisorption, and Surface Diffusion; Shustorovich, E., Ed.; VCH Publishers Inc.: New York, NY, USA, 1991; Chapter 2; pp. 53–107. [Google Scholar]
- Yagyu, S.; Yoshitake, M.; Chikyow, T. Consideration of thiol and carboxylic acid chemisorption on various electrode materials by thermodynamic calculation. J. Vac. Soc. Jpn. 2012, 55, 108–111. (In Japanese) [Google Scholar] [CrossRef]
- Shriver, D.F.; Atkins, P.W. Inorganic Chemistry, 3rd ed.; Tamamushi, R., Sato, G., Kakihana, M., Eds.; Oxford University Press: London, UK, 1999; pp. 237–239. [Google Scholar]
- Huheey, J.H. Inorganic Chemistry, Principles of Structure and Reactivity, 3rd ed.; Kodama, G., Nakazawa, H., Eds.; Harper & Row: New York, NY, USA, 1983; pp. 291–292. [Google Scholar]
- Moore, W.J. Physical Chemistry, 4th ed.; Longman Group: Great Britain, UK, 1972; pp. 608–611. [Google Scholar]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 80th ed.; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Dean, J.A. (Ed.) Lange’s Handbook of Chemistry, 12th ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Weast, R.C.; Astle, M.J. (Eds.) CRC Handbook of Chemistry and Physics, 62nd ed.; CRC: Boca Raton, FL, USA, 1981. [Google Scholar]
- Momose, M.; Noguchi, M. Electron emission during frictional contact between metals and polymers. Phys. Stat. Sol. (A) 1984, 82, K83–K86. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 5th ed.; John Wiley & Sons: New York, NY, USA, 1976; p. 170. [Google Scholar]
- Moore, W.J. Physical Chemistry, 3rd ed.; Fujishiro, R., Imamura, M., Kawaguchi, S., Nakatsuka, K., Eds.; Prentice-Hall: Engelwood Cliffs, NJ, USA, 1962; p. 516. [Google Scholar]
- Dekker, A.J. Solid State Physics; Asia, M., Ed.; Prentice-Hall: New York, NY, USA, 1957; pp. 225–228. [Google Scholar]
- Nakayama, K.; Nevshupa, R.A. Plasma generation in a gap around a sliding contact. J. Phys. D Appl. Phys. 2002, 35, L53–L56. [Google Scholar] [CrossRef]
- Tsukada, M. Shigoto Kansu (Work Function); Kyoritsu-Shuppan: Tokyo, Japan, 1983; p. 55. (In Japanese) [Google Scholar]




















| Group | 4 | - | 5 | - | 6 | 8 | - | 9 | - | 10 | - | 11 | - | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Element (Period 3) | - | - | - | - | - | - | - | - | - | - | - | - | Al | - | ||
| TriboEE (105 counts) Heat of formation of oxide/O (kJ mol−1) D(M–O) (102 kJ mol−1) | - | - | - | - | - | - | - | - | - | - | - | - | - | 3.44 ± 2.66 Al2O3(1/3) −558.5 8.07 | - | |
| Element (Period 4) | Ti | - | V | - | Fe | - | Co | - | Ni | - | Cu | - | Zn | - | - | |
| TriboEE (105 counts) | 2.45 ± 1.22 | > | 0.55 ± 0.59 | - | 6.59 ± 2.94 | < | 7.66± 0.86 | > | 3.33 ± 1.15 | < | 6.83 ± 2.61 | > | 5.79 ± 1.72 | - | - | |
| Heat of formation of oxide/O (kJ mol−1) | TiO −519.7 | - | VO −431.8 | Fe3O4(1/4) −279.6 | - | CoO −237.9 | - | NiO −239.9 | - | Cu2O −168.6 | - | ZnO −350.46 | - | - | ||
| D(M–O) (102 kJ mol−1) | 7.68 | > | 6.81 | 5.28 | > | 4.87 | ≈ | 4.89 | > | 4.18 | < | 5.99 | - | - | ||
| Element (Period 5) | Zr | - | Nb | - | Mo | - | - | - | - | Pd | - | Ag | - | - | - | Sn |
| TriboEE (105 counts) | 5.66 ± 3.87 | > | 1.13 ± 0.86 | > | 0.06 ± 0.005 | - | - | - | - | 4.32 ± 1.78 | < | 5.03 ± 2.77 | - | - | - | 6.29 ± 2.53 |
| Heat of formation of oxide/O (kJ mol−1) | ZrO2(1/2) −550.3 | - | NbO −405.6 | - | MoO2(1/2) −294.5 | - | - | - | - | PdO −85.4 | - | Ag2O −31.1 | - | - | - | SnO2(1/2) −288.8 |
| D(M–O) (102 kJ mol−1) | 7.99 | > | 6.54 | > | 5.44 | - | - | - | - | 3.35 | > | 2.80 | - | - | - | 5.38 |
| Element (Period 6) | - | - | Ta | - | W | - | - | - | - | Pt | - | Au | - | - | - | - |
| TriboEE (105 counts) | - | - | 11.84 ± 6.32 | > | 11.14 ± 5.92 | - | - | - | - | 5.11 ± 1.26 | < | 27.25 ± 6.42 | - | - | - | - |
| Heat of formation of oxide/O (kJ mol−1) | - | - | Ta2O5(1/5) –409.2 | WO2(1/2) −294.9 | - | - | - | - | Pt3O4(1/4) −40.8 | - | Au2O3(1/3) −3.01 | - | - | - | - | |
| D(M–O) (102 kJ mol−1) | - | - | 6.58 | > | 5.44 | - | - | - | - | 2.90 | > | 2.52 | - | - | - | - |
| Group | 4 | 5 | 6 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|
| Oxidation number of metal | - | - | - | - | - | - | - | - | - | - |
| Period 3 | - | - | - | - | - | - | - | - | Al | - |
| III | - | - | - | - | - | - | - | - | Al2O3(1/3) −558.6 | - |
| Period 4 | Ti | V | - | Fe | Co | Ni | Cu | Zn | - | - |
| I | - | - | - | - | - | - | Cu2O −168.6 | - | - | - |
| II | TiO −519.7 | VO −431.8 | - | FeO −272.0 | CoO −237.9 | NiO −239.9 | CuO −157.3 | ZnO −350.46 | - | - |
| II, III | - | - | - | Fe3O4(1/4) −279.6 | - | - | - | - | - | - |
| III | Ti2O3(1/3) −507.2 | V2O3(1/3) −406.2 | Fe2O3(1/3) −274.7 | - | Ni2O3(1/3) −163.2 | - | - | - | - | |
| IV | TiO2(1/2) −472.0 | VO2(1/2) −359.0 | - | - | - | - | - | - | - | - |
| V | - | V2O5(1/5) −310.1 | - | - | - | - | - | - | - | - |
| Period 5 | Zr | Nb | Mo | - | - | Pd | Ag | - | - | Sn |
| I | - | - | - | - | - | - | Ag2O −31.1 | - | - | - |
| II | - | NbO −405.6 | - | - | - | PdO −85.4 | AgO −11.4 | - | - | SnO −285.9 |
| IV | ZrO2(1/2) −550.3 | NbO2(1/2) −398.1 | MoO2(1/2) −294.5 | - | - | - | - | - | - | SnO2(1/2) −288.8 |
| V | - | Nb2O5(1/5) −379.9 | - | - | - | - | - | - | - | - |
| VI | - | - | MoO3(1/3) −248.4 | - | - | - | - | - | - | - |
| Period 6 | - | Ta | W | - | - | Pt | Au | - | - | - |
| II, IV | - | - | - | - | - | Pt3O4 (1/4) −40.8 | - | - | - | - |
| III | - | - | - | - | - | - | Au2O3 (1/3) −3.01 | - | - | - |
| IV | - | - | WO2(1/2) −294.9 | - | - | - | - | - | - | - |
| V | - | Ta2O5(1/5) −409.2 | - | - | - | - | - | - | - | - |
| VI | - | - | WO3(1/3) −281.0 | - | - | - | - | - | - | - |
| Group | 4 | - | 5 | - | 6 | 8 | - | 9 | - | 10 | - | 11 | - | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Element (Period 3) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | Al | - |
| Work function (eV) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 4.28 | - |
| Photothreshold (eV) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 4.25 | - |
| Electrical conductivity (107 Sm−1) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 3.65 | - |
| Element (Period 4) | Ti | - | V | - | - | Fe | - | Co | - | Ni | - | Cu | - | Zn | - | - |
| Work function (eV) | 4.33 | - | 4.3 | - | - | 4.5 | - | 5.0 | - | 5.15 | - | 4.65 | - | 4.33 | - | - |
| Photothreshold (eV) | 4.59 | - | - | - | - | 5.13 | - | 5.01 | - | 5.10 | - | 4.54 | - | 4.67 | - | - |
| Electrical conductivity (107 Sm−1) | 0.23 | < | 0.5 | - | - | 1.02 | < | 1.72 | > | 1.43 | < | 5.88 | > | 1.69 | - | - |
| Element (Period 5) | Zr | - | Nb | - | Mo | - | - | - | - | Pd | - | Ag | - | - | - | Sn |
| Work function (eV) | 4.05 | - | 4.3 | - | 4.6 | - | - | - | - | 5.12 | - | 4.26 | - | - | - | 4.42 |
| Photothreshold (eV) | - | - | 5.10 | - | 4.9 | - | - | - | - | 4.99 | - | 4.28 | - | - | - | 4.74 |
| Electrical conductivity (107 Sm−1) | 0.24 | < | 0.69 | < | 1.89 | - | - | - | - | 0.95 | < | 6.21 | - | - | - | 0.91 |
| Element (Period 6) | - | - | Ta | - | W | - | - | - | - | Pt | - | Au | - | - | - | - |
| Work function (eV) | - | - | 4.25 | - | 4.55 | - | - | - | - | 5.65 | - | 5.1 | - | - | - | - |
| Photothreshold (eV) | - | - | 4.58 | - | 4.60 | - | - | - | - | 5.09 | - | 4.56 | - | - | - | - |
| Electrical conductivity (107 Sm−1) | - | - | 0.76 | < | 1.89 | - | - | - | - | 0.96 | < | 4.55 | - | - | - | - |
| Group | 4 | - | 5 | - | 6 | 8 | - | 9 | - | 10 | - | 11 | - | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Element (Period 3) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | Al | - |
| F1s (103 counts) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 8.12 | - |
| O1s (103 counts) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 18.97 | - |
| C1s (104 counts) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 2.73 | - |
| metal 2p (103 counts) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 12.81 (Al2p) | - |
| O1s/metal 2p | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1.48 | - |
| Element (Period 4) | Ti | - | V | - | - | Fe | - | Co | - | Ni | - | Cu | - | Zn | - | - |
| F1s (103 counts) | 3.86 | < | 9.65 | - | - | 3.33 | > | 2.07 | < | 8.00 | < | 8.86 | > | 7.23 | - | - |
| O1s (103 counts) | 10.66 | > | 9.62 | - | - | 7.14 | < | 8.17 | < | 10.24 | > | 9.93 | > | 7.45 | - | - |
| C1s (104 counts) | 1.54 | < | 2.28 | - | - | 2.11 | ≈ | 2.14 | < | 3.38 | > | 2.08 | ≈ | 2.11 | - | - |
| metal 2p (103 counts) | 2.85 (Ti2p) | < | 3.08 (V2p) | - | - | 1.88 (Fe2p) | > | 1.32 (Co2p) | < | 1.63 (Ni2p) | > | 0.71 (Cu2p) | < | 1.18 (Zn2p) | - | - |
| O1s/metal 2p | 3.74 | > | 3.12 | - | - | 3.80 | < | 6.19 | < | 6.28 | < | 13.99 | > | 6.31 | - | - |
| Element (Period 5) | Zr | - | Nb | - | Mo | - | - | - | - | Pd | - | Ag | - | - | - | Sn |
| F1s (103 counts) | 7.60 | > | 6.35 | < | 13.40 | - | - | - | - | 9.65 | > | 9.21 | - | - | - | 11.49 |
| O1s (103 counts) | 7.21 | < | 15.17 | > | 9.90 | - | - | - | - | 5.79 | > | 2.59 | - | - | - | 11.66 |
| C1s (104 counts) | 1.66 | < | 1.94 | > | 1.33 | - | - | - | - | 1.52 | ≈ | 1.51 | - | - | - | 2.70 |
| metal3p,3d (103 counts) | 1.48 (Zr3p) | < | 4.80 (Nb3d) | > | 2.50 (Mo3d) | - | - | - | - | 3.21 (Pd3d) | < | 9.39 (Ag3d) | - | - | - | 4.56 (Sn3d) |
| O1s/metal 3p,3d | 4.87 | > | 3.16 | < | 3.96 | - | - | - | - | 1.80 | > | 0.28 | - | - | - | 2.56 |
| Element (Period 6) | - | - | Ta | - | W | - | - | - | - | Pt | - | Au | - | - | - | - |
| F1s (103 counts) | - | - | 26.91 | > | 2.28 | - | - | - | - | 23.70 | > | 12.58 | - | - | - | - |
| O1s (103 counts) | - | - | 14.62 | < | 16.93 | - | - | - | - | 3.76 | > | 2.93 | - | - | - | - |
| C1s (104 counts) | - | - | 1.97 | < | 2.20 | - | - | - | - | 2.52 | > | 1.58 | - | - | - | - |
| metal4d, 4f (103 counts) | - | - | 1.59 (Ta4d) | < | 3.65 (W4f) | - | - | - | - | 3.92 (Pt4f) | < | 5.23 (Au4f) | - | - | - | - |
| O1s/metal 4d,4f | - | - | 9.19 | > | 4.64 | - | - | - | - | 0.96 | > | 0.56 | - | - | - | - |
| Group | 4 | - | 5 | - | 6 | 8 | - | 9 | - | 10 | - | 11 | - | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Element (Period 3) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | Al | - |
| O1s (103 counts) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 18.52 | - |
| C1s (104 counts) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 3.68 | - |
| metal 2p (103 counts) | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 12.63 (Al2p) | - |
| O1s/metal 2p | - | - | - | - | - | - | - | - | - | - | - | - | - | - | 1.47 | - |
| Element (Period 4) | Ti | - | V | - | - | Fe | - | Co | - | Ni | - | Cu | - | Zn | - | - |
| O1s (103 counts) | 14.55 | < | 17.10 | - | - | 10.10 | > | 9.28 | > | 9.14 | < | 17.24 | > | 10.38 | - | - |
| C1s (104 counts) | 1.97 | < | 2.94 | - | - | 2.62 | > | 2.43 | < | 3.11 | > | 2.69 | < | 3.54 | - | - |
| metal 2p (103 counts) | 3.94 (Ti2p) | < | 5.35 (V2p) | - | - | 2.47 (Fe2p) | > | 1.33 (Co2p) | < | 1.42 (Ni2p) | > | 0.96 (Cu2p) | < | 1.37 (Zn2p) | - | - |
| O1s/metal 2p | 3.67 | > | 3.20 | - | - | 4.10 | < | 6.99 | > | 6.45 | < | 17.91 | > | 7.56 | - | - |
| Element (Period 5) | Zr | - | Nb | - | Mo | - | - | - | - | Pd | - | Ag | - | - | - | Sn |
| O1s (103 counts) | 14.14 | < | 21.97 | > | 13.76 | - | - | - | - | 10.86 | > | 4.21 | - | - | - | 17.45 |
| C1s (104 counts) | 1.88 | < | 3.07 | > | 2.63 | - | - | - | - | 2.58 | > | 1.87 | - | - | - | 3.02 |
| metal3p,3d (103 counts) | 2.95 (Zr3p) | < | 7.19 (Nb3d) | > | 3.62 (Mo3d) | - | - | - | - | 5.27 (Pd3d) | < | 13.02 (Ag3d) | - | - | - | 6.41 (Sn3d) |
| O1s/metal 3p,3d | 4.79 | > | 3.06 | < | 3.80 | - | - | - | - | 2.06 | > | 0.32 | - | - | - | 2.72 |
| Element (Period 6) | - | - | Ta | - | W | - | - | - | - | Pt | - | Au | - | - | - | - |
| O1s (103 counts) | - | - | 18.28 | > | 16.72 | - | - | - | - | 5.28 | > | 3.97 | - | - | - | - |
| C1s (104 counts) | - | - | 2.37 | > | 2.27 | - | - | - | - | 2.48 | > | 2.02 | - | - | - | - |
| metal4d,4f (103 counts) | - | - | 1.82 (Ta4d) | < | 3.09 (W4f) | - | - | - | - | 4.84 (Pt4f) | < | 11.78 (Au4f) | - | - | - | - |
| O1s/metal 4d,4f | - | - | 10.02 | > | 5.41 | - | - | - | - | 1.09 | > | 0.34 | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Momose, Y. Electron Transfer through a Natural Oxide Layer on Real Metal Surfaces Occurring during Sliding with Polytetrafluoroethylene: Dependence on Heat of Formation of Metal Oxides. Coatings 2021, 11, 109. https://doi.org/10.3390/coatings11010109
Momose Y. Electron Transfer through a Natural Oxide Layer on Real Metal Surfaces Occurring during Sliding with Polytetrafluoroethylene: Dependence on Heat of Formation of Metal Oxides. Coatings. 2021; 11(1):109. https://doi.org/10.3390/coatings11010109
Chicago/Turabian StyleMomose, Yoshihiro. 2021. "Electron Transfer through a Natural Oxide Layer on Real Metal Surfaces Occurring during Sliding with Polytetrafluoroethylene: Dependence on Heat of Formation of Metal Oxides" Coatings 11, no. 1: 109. https://doi.org/10.3390/coatings11010109
APA StyleMomose, Y. (2021). Electron Transfer through a Natural Oxide Layer on Real Metal Surfaces Occurring during Sliding with Polytetrafluoroethylene: Dependence on Heat of Formation of Metal Oxides. Coatings, 11(1), 109. https://doi.org/10.3390/coatings11010109