Approach to Heterogeneous Surface Roughness Evaluation for Surface Coating Preparation
Abstract
:1. Introduction
2. Materials and Methods
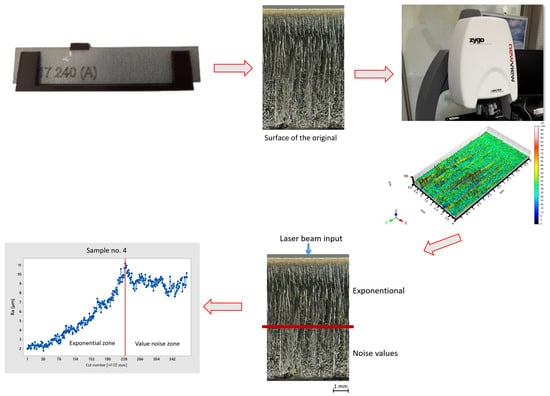
2.1. Sample Preparation for Measurement
2.2. Data Obtainment
3. Results
3.1. Exploratory Data Analysis (EDA)
3.2. Further Data Exploration
3.3. Linear Regression
3.4. Non-Linear Regression
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nazarpour, S. Introduction: What Are Coatings? In Thin Films and Coatings in Biology; Biological and Medical Physics, Biomedical Engineering; Springer: Dordrecht, The Netherlands, 2013; pp. 1–9. ISBN 978-94-007-2591-1. [Google Scholar]
- Pedroso, A.F.V.; Sousa, V.F.C.; Sebbe, N.P.V.; Silva, F.J.G.; Campilho, R.D.S.G.; Sales-Contini, R.C.M.; Jesus, A.M.P. A Comprehensive Review on the Conventional and Non-Conventional Machining and Tool-Wear Mechanisms of Inconel®. Metals 2023, 13, 585. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, Y.; Xie, J.; Xu, Q.; Fei, H.; Lu, Y.; Gong, J. Effect of Temperature, Vacuum Condition and Surface Roughness on Oxygen Boost Diffusion of Ti–6Al–4V Alloy. Coatings 2024, 14, 314. [Google Scholar] [CrossRef]
- Mičietová, A.; Neslušan, M.; Florková, Z.; Čilliková, M. Analysis of the Coating Delamination after Laser Beam Cutting. Manuf. Technol. 2023, 23, 670–675. [Google Scholar] [CrossRef]
- Bohdal, Ł.; Schmidtke, D. Effect of Fiber and CO2 Lasers Parameters on the Cut Surface Quality of Rvs 1.4301 Stainless Steel. J. Mech. Eng. Sci. 2022, 16, 8862–8872. [Google Scholar] [CrossRef]
- Wala, T.; Lis, K. Influence of Selected Diagnostic Parameters on the Quality of Awj Cutting Surface. Adv. Sci. Technol. Res. J. 2022, 16, 129–140. [Google Scholar] [CrossRef] [PubMed]
- Basmacı, G.; Kayacan, M.Y.; Ay, M.; Etyemez, A. Optimization of Cutting Forces and Surface Roughness via Anova and Grey Relational Analysis in Machining of In718. Open Chem. 2023, 21, 129–140. [Google Scholar] [CrossRef]
- Bautista, A.; Sáez-Maderuelo, A.; Monrrabal, G.; Ruiz-Lorenzo, M.L.; Perosanz, F.J.; Maffiotte, C.; Volpe, L.; Scenini, F.; Maurotto, A.; Halodová, P.; et al. Surface Characterization and Electrochemical Behavior of Aisi 316L Stainless Steel Machined with Green Supercritical CO2 Coolant. J. Mater. Eng. Perform. 2023, 21, 129–140. [Google Scholar] [CrossRef]
- Chmielewski, T.; Hudycz, M.; Krajewski, A.; Sałaciński, T.; Skowrońska, B.; Świercz, R.; Volpe, L.; Scenini, F.; Maurotto, A.; Halodová, P.; et al. Structure Investigation of Titanium Metallization Coating Deposited onto Aln Ceramics Substrate by Means of Friction Surfacing Process. Coatings 2019, 9, 129–140. [Google Scholar] [CrossRef]
- Patel, P.; Nakum, B.; Abhishek, K.; Rakesh Kumar, V. Machining Performance Optimization during Plasma Arc Cutting of Aisi D2 Steel: Application of Fis, Nonlinear Regression and Jaya Optimization Algorithm. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 240. [Google Scholar] [CrossRef]
- Anghel, C.; Gupta, K.; Jen, T.C. Analysis and Optimization of Surface Quality of Stainless Steel Miniature Gears Manufactured by CO2 Laser Cutting. Optik 2020, 203, 164049. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Ninikas, K.; Petousis, M.; Vidakis, N. Laser Cutting of 3D Printed Acrylonitrile Butadiene Styrene Plates for Dimensional and Surface Roughness Optimization. Int. J. Adv. Manuf. Technol. 2022, 119, 2301–2315. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Tsiolikas, A.; Petousis, M.; Ninikas, K.; Vidakis, N.; Tzounis, L. A Robust Methodology for Optimizing the Topology and the Learning Parameters of an Ann For Accurate Predictions of Laser-Cut Edges Surface Roughness. Simul. Model. Pract. Theory 2022, 114, 102414. [Google Scholar] [CrossRef]
- Biermann, D.; Steiner, M.; Krebs, E. Investigation of Different Hard Coatings for Micromilling of Austenitic Stainless Steel. Procedia CIRP 2013, 7, 246–251. [Google Scholar] [CrossRef]
- ISO 21920-2:2021; Specifications, Geometrical Product. “Surface Texture: Profile—Part 2: Terms, Definitions and Surface Texture Parameters”. International Organization for Standardization: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/72226.html (accessed on 10 March 2024).
- Marek, M.; Novák, M.; Šramhauser, K. The Impact of Changes in Infeed Rate on Surface Integrity after Chrome Plate Grinding by Microcrystalline Corundum. Manuf. Technol. 2019, 19, 461–468. [Google Scholar] [CrossRef]
- Timárová, Ľ.; Breznická, A.; Kopiláková, B. Application of the Method of Planned Experiment for the Evaluation of the Surface Roughness Parameter Ra. Manuf. Technol. 2023, 23, 348–353. [Google Scholar] [CrossRef]
- Allen, T.T.; Sui, Z.; Akbari, K.; Silva, F.J.G.; Campilho, R.D.S.G.; Sales-Contini, R.C.M.; Jesus, A.M.P. Exploratory Text Data Analysis for Quality Hypothesis Generation. Qual. Eng. 2018, 30, 701–712. [Google Scholar] [CrossRef]














| N | 376 |
|---|---|
| Mean | 7.343 [μm] |
| Se Mean | 0.220 [μm] |
| St. Dev. [σ] | 4.263 [μm] |
| Minimum | 1.943 [μm] |
| Q1 | 3.368 [μm] |
| Median | 6.457 [μm] |
| Q3 | 12.052 [μm] |
| Maximum | 15.264 [μm] |
| R-Sq(adj) [%] | ||
|---|---|---|
| Quadratic | Cubic | |
| Ra_1 | 95.4 | 97.7 |
| Ra_2 | 81.6 | 90.6 |
| Ra_3 | 84.2 | 87.5 |
| Ra_4 | 97.1 | 97.2 |
| Ra_5 | 89.9 | 90.3 |
| Ra_6 | 95.4 | 97.7 |
| Ra_7 | 97.1 | 97.9 |
| Ra_8 | 97.8 | 98.0 |
| Ra_9 | 96.6 | 96.9 |
| Ra_10 | 93.8 | 96.5 |
| Exponential Reg. Model | |||
|---|---|---|---|
| MSE | S | Iterations | |
| Ra_1 | 0.38 | 0.61 | 23 |
| Ra_2 | 0.74 | 0.86 | 18 |
| Ra_3 | 0.87 | 0.94 | 19 |
| Ra_4 | 0.15 | 0.39 | 17 |
| Ra_5 | 0.39 | 0.62 | 21 |
| Ra_6 | 0.38 | 0.61 | 23 |
| Ra_7 | 0.26 | 0.52 | 19 |
| Ra_8 | 0.31 | 0.56 | 22 |
| Ra_9 | 0.21 | 0.56 | 21 |
| Ra_10 | 0.54 | 0.73 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrbová, H.; Kubišová, M.; Pata, V.; Knedlová, J.; Javořík, J.; Bočáková, B. Approach to Heterogeneous Surface Roughness Evaluation for Surface Coating Preparation. Coatings 2024, 14, 471. https://doi.org/10.3390/coatings14040471
Vrbová H, Kubišová M, Pata V, Knedlová J, Javořík J, Bočáková B. Approach to Heterogeneous Surface Roughness Evaluation for Surface Coating Preparation. Coatings. 2024; 14(4):471. https://doi.org/10.3390/coatings14040471
Chicago/Turabian StyleVrbová, Hana, Milena Kubišová, Vladimír Pata, Jana Knedlová, Jakub Javořík, and Barbora Bočáková. 2024. "Approach to Heterogeneous Surface Roughness Evaluation for Surface Coating Preparation" Coatings 14, no. 4: 471. https://doi.org/10.3390/coatings14040471
APA StyleVrbová, H., Kubišová, M., Pata, V., Knedlová, J., Javořík, J., & Bočáková, B. (2024). Approach to Heterogeneous Surface Roughness Evaluation for Surface Coating Preparation. Coatings, 14(4), 471. https://doi.org/10.3390/coatings14040471