Investigation of the Tendency of Carbon Fibers to Disintegrate into Respirable Fiber-Shaped Fragments

Abstract

Recent reports of the release of large numbers of respirable and critically long fiber-shaped fragments from mesophase pitch-based carbon fiber polymer composites during machining and tensile testing have raised inhalation toxicological concerns. As carbon fibers and their fragments are to be considered as inherently biodurable, the fiber pathogenicity paradigm motivated the development of a laboratory test method to assess the propensity of different types of carbon fibers to form such fragments. It uses spallation testing of carbon fibers by impact grinding in an oscillating ball mill. The resulting fragments were dispersed on track-etched membrane filters and morphologically analyzed by scanning electron microscopy. The method was applied to nine different carbon fiber types synthesized from polyacrylonitrile, mesophase or isotropic pitch, covering a broad range of material properties. Significant differences in the morphology of formed fragments were observed between the materials studied. These were statistically analyzed to relate disintegration characteristics to material properties and to rank the carbon fiber types according to their propensity to form respirable fiber fragments. This tendency was found to be lower for polyacrylonitrile-based and isotropic pitch-based carbon fibers than for mesophase pitch-based carbon fibers, but still significant. Although there are currently only few reports in the literature of increased respirable fiber dust concentrations during the machining of polyacrylonitrile-based carbon fiber composites, we conclude that such materials have the potential to form critical fiber morphologies of WHO dimensions. For safe-and-sustainable carbon fiber-reinforced composites, a better understanding of the material properties that control the carbon fiber fragmentation is imperative.

1. Introduction

Carbon fibers (CFs) are generally used as a functional additive to various matrix materials. By incorporating carbon fibers, high material performance can be achieved, including mechanical strength, light weight, thermal and chemical resistance, thermal and electrical conductivity. As a result, carbon fiber composites, including carbon fiber reinforced polymers (CFRP), silicon carbide ceramics, carbon-carbon composites and carbon-concrete composites, are in a high and still increasing demand in several industrial sectors, such as aerospace, automotive, civil engineering and energy.

In general terms, carbon fibers mainly consist of elemental carbon in a highly cross-linked sp²-hybridized state, partly in an ordered graphitic, partly in a turbostratic configuration. Unlike polymer fibers, which, depending on the initial monomer, also contain a high proportion of carbon atoms, the art of synthesizing CFs requires a heat treatment of the hydrocarbon precursors without slackening or burning a spun filament in order to remove the majority of non-carbon atoms and to cross-link the product. Typically, precursors are spun and drawn into filament yarns. Microstructural order can be promoted by liquid crystal properties of the precursor molecules, chemitactical alignment and yarn stretching. Spinning and drawing are followed by heat treatments in oxidative and inert gas atmospheres to cross-link, carbonize and graphitize the filaments. Manufacturers have optimized their manufacturing processes in terms of desired product properties and cost.

Various CF precursors are used in mass production, including PAN, pitches, lignin or rayon. The two most industrially relevant precursors are polyacrylonitrile (PAN) and mesophase pitch. PAN-based carbon fibers (panCFs) have a market share of about 95%, while pitch-based CFs (pitchCFs) have a market share of about 4% [1]. Other precursors are still under development or have obtained only a small market share [2,3,4].

After manufacture, CFs are generally coated with polymers by so-called textile warp sizing to reduce abrasion, interyarn friction and breakage during winding on the bobbins or during weaving, stitching etc. In addition, sizing aims at adapting the chemical surface functionality and polarity of CFs to obtain chemically reactive or at least wettable CF surfaces for various composite matrix materials such as thermoplastics, thermosetting polymers or cements.

Variations in precursor, spinning, thermal treatments and sizing have resulted in a very wide range of products, with large differences in the material’s bulk and surface properties of the material, all of which are subsumed under the term “carbon fiber”. This wide material range of offers many choices for companies producing composites, semi-finished or finished products. For example, some satellites require lightweight structures that also act as heat spreaders and compensate for varying solar irradiative heating. They use CFs with very high tensile modulus and thermal conductivity and low coefficient of thermal expansion, properties mainly provided mainly by pitchCFs. Automotive applications, on the other hand, rely on low-cost CFs of lower stiffness but with high tensile strength, properties provided mainly by panCFs. At the design stage of a CF-containing product, the type of CF is generally carefully selected in terms of material properties and costs. However, during the processing, use, recycling and end-of-life phases of a product, information on the type of embedded CF is usually not available or not communicated.

This is critical from an occupational health and safety perspective, as striking differences in the fragmentation characteristics of panCFs and pitchCFs have been reported in literature [5,6,7,8]. CFs must therefore be considered to exhibit a material-specific risk profile with respect to their propensity to form respirable fiber-shaped fragments including “WHO-fibers”, i.e., fibers with dimensions according to the WHO fiber counting convention [9]. In particular, workers handling, machining, shredding or incinerating fiber-containing products must be protected from inhalative exposure to respirable biodurable fibers with WHO dimensions.

Taking into account measurement errors, the length L of a WHO-fiber satisfies (L + ΔL) ≥ 5 µm, its diameter 𝐷 satisfies (D − ΔD) ≤ 3 µm and its aspect ratio $AR$ satisfies L/D⋅(1+ΔL/L+ΔD/D) ≥ 3. Fibers satisfying the latter relation are called High Aspect Ratio (HAR) fibers. Respirability describes the potential of fibers to reach the alveolar region of the deep respiratory tract. Fibers that are not too long, with a diameter of less than 3 $\mathrm{\mu }\mathrm{m}$ and a specific density of 2.6 g/cm³ are considered respirable. These values originate from toxicologically well-studied vitreous fibers. There is no consensus in the literature on the maximum respirable fiber length. Fibers of 100 µm length and 3 µm diameter were reported to reach the alveolar region [10]. The cut-off fiber diameter of 3 µm may need adaption for materials with lower density than 2.6 g/cm³ due to higher buoyancy in air.

A fiber is said to be biopersistent if its material is insoluble in tissue fluids over long time scales, i.e., biodurable, and if the fiber cannot be removed from an alveolus by phagocytic clearance for morphological reasons, e.g., if its length exceeds the size of an alveolar macrophage.

Fibers that persist in the deep airways may become the cause of a chronic inflammation and may increase the risk of developing granuloma, asbestosis and mesothelioma [11]. Such fiber-characteristic pathogenicity is infamously known for asbestos [12,13,14,15,16].

Data in the literature on the toxicological relevance of CFs are sparse and inconsistent. Studies on pathological effects were reported by, e.g., [17,18,19,20,21,22,23,24,25]. Some authors have criticized the adequacy of such studies [26,27]. The authors of [28] reviewed the available toxicological literature on carbon fibers with focus on fiber length.

Indeed, the methodologies used for toxicological testing of inhalation-related fiber risks in laboratory studies have sometimes been questionable, e.g., when inhalation exposure of animals was studied with non-respirable fibers of original diameter of about 3.5 µm [20,29] or 6–8 µm [22,30], or fibers that were several millimeters long [29]. Cell culture experiments with fiber-shaped CF fragments are discussed as a substitute to animal studies, e.g., [24,25]. However, the relevance of observing no effects or only transient inflammation in short-living cell cultures for predicting long-term effects in the deep lung tissue is unclear.

Also for occupational exposure situations, the number of published studies is surprisingly small. Studies on the release of respirable fragments from CF or CFRP include [8,23,24,31,32,33,34,35,36,37,38,39,40,41,42]. The authors of [7,35] observed submicron fibers from machined nano- and microscale fiber composites, whereas earlier works reported that the original fiber diameters were maintained even during very different machining operations [33].

It is plausible that the observation of a release of respirable carbon fiber fragments depends on the details of the CF and composite matrix type, material amount and machining energy impact, ventilation and sampling conditions. For instance, no release was observed during continuous filament production and [32], whereas high release was observed during shredding of CFRP [24]. The majority of studies were also performed with the most common types of panCFs, so data on pitch-based CFs is sparse. A compilation of results of measurement performed between 1994 and 2011 at different industrial workplaces reported the observation of significant release of fiber-shaped fragments from machining carbon or glass-fiber (GF) reinforced composites [40]. These data requires further differentiation into CF and GF release but emphasize the importance of exposure assessment for workplaces handling CF materials.

The lack of epidemiological evidence, systematic toxicological studies on CF fragments and sparse data on exposure assessment are reasons why currently no occupational exposure limits (OELs) have been implemented for CFs. However, as a precautionary measure, some countries have established recommended exposure limits for fiber types that are not otherwise regulated [43]. For example, the “Recommendation from the Scientific Committee on Occupational Exposure Limits for man-made mineral fibers (MMMF) with no indication for carcinogenicity and not specified elsewhere” [44] recommends a value of 1 fiber per cm³. The German “Technical Rules for Hazardous Substances” (TRGS 905) [45] recommend that all inorganic fiber dusts with WHO dimensions but insufficient toxicological data are classified as carcinogenicity class 2 of the European CLP Regulation (“Classification, Labelling and Packaging” [46]).

In this context, the term fiber refers not only to the fibers of the product, but also to fibrous fragments formed from a material. Precautionary measures appear justified by the fiber pathogenicity paradigm [11,47,48], which states that the elongated shape of fibers is a carcinogenic principle for respirable and biodurable fibers. It is considered to be independent of the compositional details of an inert material and therefore implies generalizability in the absence of material-specific toxicological data. From an occupational hygiene perspective, all fibers meeting the criteria of the principle must be handled with appropriate care. Fibers of potential toxicological relevance also include carbon fibers that may have been thinned to a respirable diameter by a thermal and/or oxidative process [26,49], fibers that are intrinsically highly chemically inert or that develop such inertness as a result of cross-linking, crystallization or other stabilizing treatment, and materials that may release respirable fibrous fragments, for example during machining [50,51,52,53].

Following a safety-by-design concept, the majority of CFs are manufactured as textile fibers of controlled diameter in a range between 5 and 11 μm and can therefore be considered non-respirable when intact. However, in situations of mechanical overload, CFs will disintegrate and exhibit a material-specific fragmentation behavior. Firstly, CFs can break cleanly and perpendicular to the fiber axis. The fragments formed will generally vary in length but will retain the original fiber diameter in two directions. Fragments with an aspect ratio of about 0.5 and above will remain non-respirable, whereas disc-like particles with higher aspect ratios will exhibit platelet-like morphology and pose an inhalation risk. Secondly, CFs can disintegrate mostly perpendicular to the fiber axis into fibrous objects. For CFs thicker than 5 µm, the fragments formed may meet WHO-criteria both in diameter and length. Thirdly, if CF disintegration occurs predominantly in the direction of the fiber axis, the length of the fibrous fragments may exceed the diameter of the initial fiber. Fourth, CFs may shatter into granular, non-fibrous fragments of low aspect ratio morphology, some of which may be respirable. During the mechanical failure of CFs, all of these modes will contribute in varying proportions depending on the load profile, material properties and microstructural details.

Depending on the morphology and dimensions of the fragments formed, different toxicological concerns and dust exposure regulations must be considered and complied with. Non-respirable dusts that do not reach deep lung tissues are of less concern, whereas respirable granular biopersistent particle (GBP) dusts are subject to mass-based exposure limits. Whenever fragments, splinters or shivers are formed from a specific CF or composite material that exhibit WHO-dimensions, the inhalative exposure to such dusts must be assessed and controlled on the basis of WHO-fiber number concentrations. The precautionary principle requires that appropriate safety measures be taken when such potentially harmful exposure is to be expected or detected.

Recently, the reported high rate of release of respirable fiber fragments from a specific type of pitch-based CF [7] has raised new awareness for occupational hygiene requirements during the machining and tensile testing of CF composites. The large variety of CF types available, the wide range of material properties and the different nature of PAN and pitch precursors motivated detailed investigations of their fragmentation characteristics. The differences observed and reported in the following highlight the need to better understand which material properties influence the tendency to form respirable fragments. In particular, the microstructure of a fiber, its crystallite size and orientation are considered to play a central role. It is of high practical relevance to clarify whether the tendency of a carbon fiber to produce fragments with WHO-dimensions can be predicted from its material properties alone.

The present study addresses these questions by correlating the material properties and microstructures of nine different commercial CF types with the results of a spallation tendency assessment method developed during the study. To assess the propensity of CFs to form respirable fibers and WHO-fibers, a kind of worst-case scenario was simulated by grinding the CFs in an oscillating ball mill. Unlike a single machining process such as sawing or drilling, in an oscillating ball mill the materials are subjected to repeated impact, shear and friction processes from all possible directions. Furthermore, it is a process that can be continued until a selected degree of disintegration is achieved. The state of disintegration chosen in the present work allowed the morphology of a representative number of fragments to be characterize with reasonable effort.

Formed fragments were analyzed by means of scanning electron microscopy (SEM) imaging. Granular, non-fibrous objects were counted, while fibrous fragments were morphologically characterized by trained personnel to collect data on their length, diameter, agglomeration state and fracture surface characteristics. They were classified into different fragment classes and the proportion of WHO-fibers was determined. All class counts are then reported normalized to either the volume or total length of the milled CF material quantity. The number of WHO-fibers formed per volume or total length of milled CF is an ostensive measure of the tendency of a CF to produce fibrous fragments of potentially high toxicological relevance. This measure can then be correlated with the amount of CFs that disintegrated in a particular process to compare the results of a worst-case release scenario with the actual workplace exposure situation.

In this paper, the disintegration characteristics of nine different commercial CF types during ball milling are studied in order to rank the materials with respect to their propensity to form dusts containing respirable fibrous fragments. Different statistical techniques are combined to investigate possible correlations between CF material properties and morphological characteristics of the fragments formed.

2. Materials and Methods

2.1. Materials

Nine different types of CFs were studied. Five were synthesized from PAN and four from pitch precursors. Three of the pitchCFs were prepared from mesophase pitch (mPitchCF), a high polymer liquid crystal pitch. The fourth pitchCF was prepared from isotropic pitch (iPitchCF) [54], a pitch that does not exhibit liquid crystal properties. The nine CFs were selected to cover a wide range of mechanical properties and manufacturers, including SGL Carbon (Wiesbaden, Germany), Teijin Limited (Osaka, Japan), Mitsubishi Chemical Corporation (Tokyo, Japan) and Nippon Graphite Fiber Corporation (NGF, Himeji, Japan), as each company’s manufacturing processes are likely to be different. Some CFs were purchased on the open market and some were provided free of charge by the manufacturers. All fibers were used as received without any further treatment. Section 3.1 gives an overview of the fibers tested and their mechanical properties.

2.2. Measurements of Material Properties

Many material properties can determine or correlate with specific aspects of the fracture behavior of a CF under mechanical failure. Relevant properties include tensile strength, tensile modulus, elongation at break, density, specific electrical resistance, thermal volume conductivity and crystallographic properties, such as lattice plane spacing (d₀₀₂), crystallite sizes (L_c, L_a||, L_a⊥), degree of partial orientation (O_P) and microporosity. To investigate such correlations, these properties were measured by experts or taken from the manufacturer’s specifications.

All material density data were taken from the data sheet provided by the manufacturer or supplier.

Tensile strength ${\sigma }_T$, (longitudinal) tensile modulus E_L and elongation at break ${\epsilon }_{\mathrm{B}}$ were measured using a tensile test with fully impregnated rovings according to DIN EN ISO 10618 [55]. The testing machine was a Zwick TC-FR250SN.A4K (Zwick Roell Group, Ulm, Germany) and the extensometer was a makroXtens BT2-EXMACRO.H11 (Zwick Roell Group, Ulm, Germany). The test speed was set to 100 mm/min and the initial load was 2 cN/tex. Tensile strength refers to the maximum mechanical tensile stress a material can be loaded before it fails. For CFs it describes the stress level at the point of strain where a fiber begins to reduce in diameter. This occurs in the plastic deformation regime and therefore in the non-linear part of the stress-strain relationship.

Specific electrical resistivity was measured by four-terminal sensing using an RLC 100 (Digimess Instruments Limited, Leicester, UK).

Thermal volume conductivity q_T is generally not a key property for panCF applications. It is usually specified by the manufacturers mostly for pitchCFs. As we had no possibility to measure it, some thermal conductivity values of panCFs were missing. However, the high linear correlation observed between the electrical volume conductivity q_E and the thermal volume conductivity q_T with a Pearson correlation coefficient of 0.999 was used to interpolate the missing thermal values for panCFs 5, 8 and 15 from the known values of the other CFs by applying the formula q_T = (q_E⋅1284.8 W·µΩ/K − 58.2 W/m/K), see Figure S2 in the Supplementary Information. For the CF materials studied, sufficiently small crystalline domains with L_C < 30 nm apparently cause only small phonon-related heat transfer effects that lead to deviations from linearity and justify this approach.

Crystallographic parameters were measured in transmission with X-ray diffractometry (D/MAX Rapid II, Rigaku, Tokyo, Japan) using a copper anode emission (λ_Cu,Kα = 0.15406 nm, U_acc = 40 V, I_acc = 30 mA), 0.8 collimator and image plate detector. The scan rate was 0.2°/min with a scan increment of 0.1°. Each measurement took 5 h and was analyzed using the instrument manufacturer’s 2DP software. For peak integration, Pearson-VII curves were fitted in a 2θ-range from 10° to 100°.

The interlayer spacing d₀₀₂ was calculated from the Bragg condition d₀₀₂=λ/(2 sinθ_c) for the [002]-reflex at the scattering (Bragg) angle ${\theta }_{\mathrm{c}}≔{\theta }_{002}$. The symbol ${\beta }_{\mathbf{c}}≔{\beta }_{002}$ denotes the full width at half maximum (FWHM) of the selected reflection peak. The associated crystallite size (stacking height) L_C was calculated using the Scherrer equation for this reflex [56]. For the lateral crystallite dimensions perpendicular ($L_{\mathrm{a}\perp }$) or parallel ($L_{\mathrm{a}\Vert }$) to the fiber axis, the [110]- or [100]-reflex was used, respectively

$$L_{\mathrm{c}}≔{\mathrm{L}}_{002}=\frac{K_{\mathrm{c}}·\lambda }{{\beta }_{\mathrm{c}}·\cos {\theta }_{\mathrm{c}}}, L_{\mathrm{a}\Vert }≔{\mathrm{L}}_{100}=\frac{K_{\mathrm{a}}·\lambda }{{\beta }_{100}·\cos {\theta }_{100}}, L_{\mathrm{a}\perp }≔L_{110}=\frac{K_{\mathrm{a}}·\lambda }{{\beta }_{110}·\cos {\theta }_{110}}.$$

(1)

The Scherrer shape factors depend on the crystallite shape and were chosen to be K_a = 1.84 and K_C = 0.9 [57]. The microporosity of a carbon fiber $P_{\mu }$ was calculated from the specific material densities $\varrho$ (${\varrho }_{Gr}={2.26 \mathrm{g}/\mathrm{c}\mathrm{m}}^3$) and the interlayer spacings d₀₀₂ of the analyzed CF and the theoretical spacing of perfect graphite (d_002,Gr = 0.335 nm)

$$P_{\mathrm{\mu }}=\frac{d_{002,\mathrm{CF}}}{d_{002,\mathrm{G}\mathrm{r}}}·\frac{{\varrho }_{\mathrm{CF}}}{{\varrho }_{\mathrm{Gr}}}$$

(2)

The partial orientation $O_{\mathrm{P}}$ was determined by an azimuthal (horizontal) scan over the [002]-reflex. The symbol $\beta$ denotes the FWHM of this azimuthal scan

$$O_{\mathrm{P}}=\frac{180°-\beta }{180°}$$

(3)

The transverse tensile modulus $E_{\mathrm{T}}$ of the materials was calculated by using an interpolation to the data of Ref. [58] in the form of E_T = 90.461 – 28.617 · log₁₀(E_L), where E_L is the (longitudinal) tensile modulus.

Raman measurements were performed with a fiber-coupled WITec Apyron 300RA confocal Raman microscope (WITec GmbH, Ulm, Germany) equipped with a 300 mm focal length spectrometer (UHTS 300), a 600 lines/mm grating and an EMCCD camera using 0.5 mW laser power at 532 nm. The high signal-to-noise spectra were obtained from averaging a series of 210 spectra with an integration time after removing the spectra affected by cosmic ray spikes. The G- and D-band area ratios $A_{\mathrm{G},\mathrm{B}\mathrm{W}\mathrm{F}}/A_D$ were determined by fitting the spectra with a superposition of a constant offset value with 7 Lorentzian peaks and, for the G band, one Breit-Wigner-Fano (BWF, [59]) line profile using

$$I_{\mathrm{B}\mathrm{W}\mathrm{F}}\left(\Gamma ,Q,\tilde{\nu }\right)≔{\left(1-\frac{2\left(\tilde{\nu }-\raisebox{1ex}{$\Gamma $}\!\left/ \!\raisebox{-1ex}{$2Q$}\right.\right)}{Q·\Gamma }\right)}^2/\left(1+\frac{4{\left(\tilde{\nu }-\raisebox{1ex}{$\Gamma $}\!\left/ \!\raisebox{-1ex}{$2Q$}\right.\right)}^2}{{\Gamma }^2}\right).$$

(4)

Here, the term $\tilde{\nu }-\Gamma /\left(2\mathrm{Q}\right)$ serves to shift the center wavenumber of the BWF profile (${\tilde{\nu }}_{\mathrm{B}\mathrm{W}\mathrm{F}}$) that does not coincide with the position of its maximum (${\tilde{\nu }}_{\mathrm{m}\mathrm{a}\mathrm{x}}$).

The graphs and calculations in the ‘Results’ and ‘Discussion’ sections have been produced using data-derived or estimated margins of error. A description of the applied error model used is given in the Supplementary Information.

2.3. Fragmentation Characterization

Here, a method is presented that aims to assess the morphology of a fractured CF material. This requires the characterization and categorization of all fragments formed in a process in terms of their morphology and potential hazardous fragment properties. On the basis of such morphological data, CF materials that disintegrated under specific mechanical overload conditions are to evaluated with respect to their likelihood to form fiber-shaped fragments, in particular of WHO dimensions. In the present work, data were collected on various morphological characteristics, including the propensity to form wedge-shaped, long and diameter-reduced fragments, and fragments that indicate spallation along the fiber axis, see Section 2.3.6.

The aim of such a study is to identify and investigate possible relationships between material properties, processing parameters and observed fragment morphology.

Mechanical overload conditions leading to CF disintegration and the formation of fragments can be established in very different ways: Firstly, technically relevant steps for fibers like cutting, laying or weaving, and composites like abrasion, drilling or cutting, secondly, reference test methods like tensile testing, three-point-bend testing, puncture resistance. Here a third class of test method was applied to study CF disintegration: A well-standardizable, easy to implement and highly reproducible laboratory ball mill grinding test. Its practical relevance is discussed in more detail in Section 4.9.

The present investigation exemplifies how morphological fragmentation data can be compiled and correlated material properties of CFs for a specific mechanical processing scenario. Future studies could apply our approach to other, practically more relevant but more complex real-world machining steps.

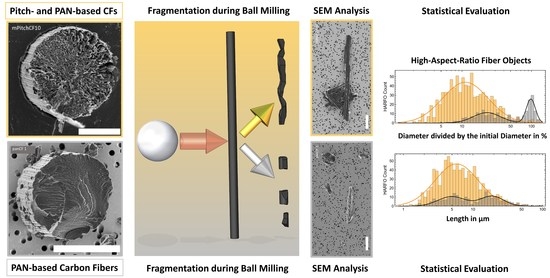
2.3.1. Structural Disintegration by Milling

An oscillating ball mill (MM200, RETSCH GmbH, Haan, Germany) with 10 mL zirconium oxide grinding jars and two zirconium oxide grinding balls of 10 mm diameter per jar was used to grind CF materials for 90 s at a vibration frequency of 25 Hz. By grinding identical CF volumes, the same volumetric energy density was applied to all materials tested. CF rovings of known filament number $n$ and filament diameter d_i were cut to a length h to obtain a volume of $V=\frac{\pi }{4}{d}_i^2·h·n={35 \mathrm{m}\mathrm{m}}^3$. The total length of the milled fibers was L_tot = h · n.

2.3.2. Suspension and Filtration

A suspension of $5 \mathrm{m}\mathrm{g}$ of the ground CF powder was prepared at a concentration of 0.5 mg/mL in 2-propanol. An aliquot of 0.1 mL of this suspension, containing approximately m_F = 55 µg ground CFs, was taken with a syringe from the center of the freshly shaken vial before sedimentation of larger fragments and diluted with 30 mL of 2-propanol. This diluted suspension was vacuum-filtrated onto gold-coated track-etched membrane filters of 25 mm diameter and 400 nm pore size (APC GmbH, Eschborn, Germany). The suspension was gradually added to the funnel and finally rinsed with a further 20 mL of 2-propanol.

2.3.3. SEM Analysis and Morphological Characterization

Subsequent SEM analysis of the membrane filters was performed using a Hitachi SU8230 (Hitachi High-Technologies Europe GmbH, Krefeld, Germany). A total of 25 randomly distributed filter locations were imaged with a size of 5120 × 3840 pixels and two different magnifications of 800×, corresponding to a pixel resolution of ΔP_800× = 31 nm, and 400×, corresponding to ΔP_400× = 62 nm, at an electron beam energy of 2 keV and a working distance of 8 mm using in-house developed software for automated stage control and image acquisition.

The evaluation of SEM images was performed visually by trained personnel, supported by an in-house developed object morphology analysis software. On each acquired image, all visible fibers and particles were registered according a set of specific counting rules, as described in detail in the Supplementary Information. Briefly, all objects were counted and the two lateral dimensions length $L$ and width $D$ of their SEM projection image were measured. As the accuracy of the length and diameter is limited by the achieved pixel resolution ΔP, measurement errors of ΔL = 15·ΔP and ΔD = 3·ΔP were assumed. The morphological data on length and diameter were used to categorize each object either as high aspect ratio fiber objects (HARFOs) with L/D·(1 + (ΔL/L + ΔD/D)) ≥ 3, or as low aspect ratio particle objects (LARPOs) with L/D·(1 + (ΔL/L + ΔD/D)) < 3. These relations result when error propagation of the aspect ratio function AR(L,D) ≔ L/D is taken into account.

For visual evaluation, a minimum of 500 objects per milled CF material were counted on as many SEM images as necessary to reach this number. Each image was evaluated in its entirety. Therefore, in general, more than 500 objects were recorded.

For imaging, an average suspended mass of m_F = 55 µg of ground CFs was vacuum filtered on a membrane filter of d_F = 25 mm diameter, corresponding to a mass area density of $\delta =\frac{4m_{\mathrm{F}}}{\pi d_{\mathrm{F}}^2}=112\frac{\mathrm{n}\mathrm{g}}{{\mathrm{m}\mathrm{m}}^2}$. On average, a filter area 0.321 mm² was evaluated, corresponding to approximately 17 SEM images with 334 × 10⁶ pixels. All object counts obtained for a specific experiment were thus renormalized to these average values. The correction factors are listed in

Table 1. The following correction factors for object counts when normalized to 55 µg and 32 mm² arise from the actually weighted mass per filter and evaluated filter area.

Fiber ID	12 iPitch	1 PAN	8 PAN	5 PAN	4 PAN	15 PAN	14 mPitch	11 mPitch	10 mPitch	Mean
Mass on Filter [mg]	0.055	0.050	0.050	0.050	0.050	0.050	0.050	0.040	0.100	0.055 ± 0.017
Evaluated Filter Area [mm2]	0.283	0.151	0.718	0.265	0.189	0.359	0.132	0.189	0.605	0.321 ± 0.207
Count Correction Factor	1.133	2.338	0.492	1.336	1.870	0.984	2.671	2.338	0.292

.

At a pixel size of ΔP = 31 nm, one evaluated SEM image of 5120 × 3840 pixels corresponds to a filter area of A_E = 0.0189 mm² and gives a mass per image of approximately m_E = A_E·δ = 1.9 ng.

Using the specific density $\varrho$ and the initial CF diameter $d_{\mathrm{i}}$, the resulting number of objects counted in a specific morphological category after $N_E$ images have been evaluated is normalized to the evaluated milled CF length $\mathcal{l}=\frac{4}{\pi ·d_{\mathrm{i}}^2}·\frac{N_{\mathrm{E}}·m_{\mathrm{E}}}{\varrho }$, or to the evaluated milled CF mass in $(N_{\mathrm{E}}·m_{\mathrm{E}})$ in the following. The length of CFs required to be milled to form 10,000 WHOFOs will also be referred to, see the ‘Discussion’ section.

2.3.4. Direction of Fragmentation

Based on the fragment shapes and morphologies as imaged by SEM, Ref. [7] assumed that mPitchCF preferentially formed fragments in the direction of the CF axis. To test this hypothesis, the maximum allowed fracture angle of a fragment was defined as $\phi ≔\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n} (d_{\mathrm{i}}/L)$, using the ratio of the initial CF diameter $d_{\mathrm{i}}$ and the measured fragment length $L$, see Section 4.4.3. For fragments shorter than the initial CF diameter, this hypothetical fracture angle was set to φ = 90° as they do not support the assumption that the CF disintegration occurred with a directional component parallel to the fiber axis.

2.3.5. Wedge-Shaped Fragments

Wedge-shaped objects are traditionally called “Krumme Hunde” (“culebra cigar”) among German fiber exposure assessment experts. They formally meet the WHO fiber condition of a length-to-diameter ratio greater than 3, but at small aspect ratios they bear little resemblance to a fiber-like object due to their wedge-like shape.

The degree of similarity to fiber-like objects was assessed in terms of the parallelism of flanks. A wedge-shape of a fragment was determined by estimating its opening angle using the following approach. The fragment was rectified along its central spine and several diameter (width) values were determined orthogonally to this backbone. The arctangent of the slope of the linear fit of these diameter values to the path length gave an estimate of the opening angle of a wedge, see Section 3.2.2.

For the subsequent discussion, the percentage of wedge-shaped fragments with an opening angle greater than 10° is determined.

2.3.6. Fragment Analysis and Compilation of Morphological Statistics

A very detailed evaluation of SEM images of milled CFs products was used to provide statistical information of the size and morphology of CF fragments. By categorizing the fragments in terms of respirability, aspect ratio and WHO dimensions, differences in CF fragmentation were investigated and related to material properties.

The following information was collected:

• Number and diameter of low aspect ratio fragments, i.e., LARPOs
• Number, length and diameter of high aspect ratio fragments, i.e., HARFOs.

LARPOs and HARFOs of approximately the original fiber diameter in one direction were referred to as “Chunks” (HARFCs or LARPCs). They are assumed to be the result of a cleanly broken carbon fiber, whereas “Splinter”-like fragments with a diameter below the original are referred to as HARFSs. A standard error of 10% was assumed on the CF original diameter to test for width similarity.

From the HARFO data the following subsets were formed

• HARFCs: HARFOs with diameters of the initial CF
• HARFSs: HARFOs with diameters below that of the initial CF
• Respirable HARFOs: HARFOs thinner than 3 µm
• WHOFOs: respirable HARFOs longer than 5 µm
• Respirable HARFOs too short to be WHOFOs, i.e., shorter than 5 µm
• Wedge-shaped HARFOs with opening-angle above 10°.

The data from these sets have been used to calculate observables to describe and study the fragmentation characteristics of the nine materials studied, including, e.g., the proportion of WHO-fibers in all high aspect ratio fragments, the ratio of fibrous to particulate fragments etc. Most of the following discussion will focus on such HARFSs, which result from disintegration pathways that lead to thinner fibrous objects, and especially on those fragments that exhibit WHO fiber dimensions.

3. Results

3.1. Material Properties

Table 2. Selected mechanical and physical properties data of the investigated carbon fibers. An asterisk (*) denotes data taken from the manufacturer’s technical specifications. Thermal conductivity was either taken from the technical specification or, for panCF 5, 8 and 15, estimated assuming a linear correlation with the electrical volume conductivity that was found for the manufacturer’s values, see text. The latter are emphasized by a blue background. Linear scale bars visualize relative magnitudes per column.

Fiber ID	Product	Tensile Modulus [GPa]	Specific Density * [g/cm3]	Thermal Conductivity * [W/m/K]	Transverse Modulus [GPa]	Electrical Resistivity [µΩ m]	Elongation at Break [%]	Tensile Strength [MPa]	Initial Diameter [µm]
12 iPitch	Mitsui GRANOC XN-05-30S	54	1.65	5.0	40.9	28.0	2.0	1100	10.0
1 PAN	Teijin Carbon Tenax HTS40 F13	240	1.77	17.0	22.3	16.4	1.8	4400	7.0
8 PAN	SGL Carbon SIGRAFIL CT50-4.0/240	240	1.77	26.0	22.3	15.3	1.7	4000	7.0
5 PAN	Teijin Carbon Tenax IMS65 E23	290	1.77	35.0	20.0	13.8	2.1	6000	5.0
4 PAN	Teijin Carbon Tenax UMS40 F23	390	1.79	46.6	16.3	10.8	1.1	4500	4.9
15 PAN	Teijin Carbon Tenax UMS55	550	1.91	107.0	12.0	7.8	0.7	4000	4.4
14 mPitch	Mitsui YSH-50A-60S	520	2.10	120.0	12.7	7.0	0.7	3830	7.0
11 mPitch	Mitsubishi Chemical Dialead K63712	640	2.12	140.0	10.2	6.6	0.4	2600	11.0
10 mPitch	Mitsubishi Chemical Dialead K13D2U	935	2.20	800.0	5.4	1.5	0.4	3700	11.0

presents data on the mechanical and physical properties of the CF materials studied, together with the associated identification codes used in this work. Subsequent tables present numerical data together with a linear scale bar to visualize relative magnitudes within a property column or a group of columns.

The investigated fibers 1, 4, 5 and 8 are typical panCFs within the range of common properties for such fibers. Fiber 15 is a panCF that was not commercially available on the European market. In terms of mechanical properties, panCF 15 is similar to mPitchCFs 14, a fiber at the lower end of the mPitchCF property range. Fiber 11 is an average mPitchCF, while fiber 10 is a high-end mPitchCF achieving very high tensile modulus and thermal conductivity. Fiber 12 is based on isotropic pitch.

Table 2 shows a clear distinction between PAN- and pitch-based CFs in terms of mechanical, electrical and thermal properties, with the mentioned exception of fibers 12 and 15. PanCFs generally exhibit higher tensile strength and elongation at break, whereas mPitchCFs exhibit higher tensile modulus, lower elongation at break and significantly better electrical and thermal conductivities. CFs that have undergone a high-temperature graphitization step tend to exhibit significantly higher material density. As the thermal conductivity data provided by the manufacturers was incomplete for some panCFs, the missing values were estimated by assuming a linear correlation with the electrical conductivity, see Section 2.2. The order of the CF materials in Table 2 corresponds to increasing tensile modulus, increasing density and decreasing electrical resistivity. The same order of CF materials is used in all subsequent tables of this format.

Table 3. Crystallographic properties obtained by XRD measurements of the fibers studied in this report.

Fiber ID	${\mathit{L}}_{\mathit{c}}\left[\mathbf{n}\mathbf{m}\right]$	${\mathit{L}}_{\left|\right|}\left[\mathbf{n}\mathbf{m}\right]$	${\mathit{L}}_{\perp }\left[\mathbf{n}\mathbf{m}\right]$	$2\mathsf{\Theta }[°]$	$\mathrm{P}.\mathbf{Orient}.{\mathit{O}}_{\mathrm{P}}[\%]$	${\mathit{d}}_{002}\left[\mathbf{n}\mathbf{m}\right]$	$\mathbf{Microporosity} {\mathit{P}}_{\mathit{\mu }}[\%]$
12 iPitch	1.36	2.9	1.6	25.3	57	0.353	23.1
1 PAN	1.36	2.9	2.3	25.4	80	0.351	17.9
8 PAN	1.61	3.5	2.4	25.5	81	0.349	18.4
5 PAN	1.55	3.3	1.8	25.6	83	0.348	18.6
4 PAN	2.87	6.2	6.6	25.8	88	0.345	18.4
15 PAN	5.36	11.5	8.0	26.0	93	0.342	13.7
14 mPitch	9.91	21.2	13.0	25.9	94	0.343	4.9
11 mPitch	11.64	24.9	12.6	25.9	95	0.344	3.7
10 mPitch	13.70	29.3	39.3	26.3	97	0.338	1.8

follows the ordering of materials in Table 2 to give an overview of the crystallographic properties obtained from XRD measurements. Pairwise correlation tests between the properties of Table 2 and Table 3 in Section 4.3.1 indicate that many of the XRD parameters are highly correlated with each other and/or with the material density as well as with mechanical properties such as tensile modulus and elongation at break.

The interlayer distance d₀₀₂ is related to the degree of graphitization (DoG) of the carbon fibers. The value of d₀₀₂ decreases with the (DoG) and approaches that of perfectly oriented graphite of 0.335 nm.

Table 4. Raman spectral area and intensity ratios of fitted Raman D- and G-bands, see text.

Fiber ID	${\mathit{L}}_{\mathit{c}}\left[\mathbf{n}\mathbf{m}\right]$	${\mathit{L}}_{\left|\right|}\left[\mathbf{n}\mathbf{m}\right]$	${\mathit{L}}_{\perp }\left[\mathbf{n}\mathbf{m}\right]$	$2\mathsf{\Theta }[°]$	$\mathrm{P}.\mathbf{Orient}.{\mathit{O}}_{\mathbf{P}}[\%]$	${\mathit{d}}_{002}\left[\mathbf{n}\mathbf{m}\right]$	$\mathbf{Microporosity} {\mathit{P}}_{\mathit{\mu }}[\%]$
12 iPitch	1.36	2.9	1.6	25.3	57	0.353	23.1
1 PAN	1.36	2.9	2.3	25.4	80	0.351	17.9
8 PAN	1.61	3.5	2.4	25.5	81	0.349	18.4
5 PAN	1.55	3.3	1.8	25.6	83	0.348	18.6
4 PAN	2.87	6.2	6.6	25.8	88	0.345	18.4
15 PAN	5.36	11.5	8.0	26.0	93	0.342	13.7
14 mPitch	9.91	21.2	13.0	25.9	94	0.343	4.9
11 mPitch	11.64	24.9	12.6	25.9	95	0.344	3.7
10 mPitch	13.70	29.3	39.3	26.3	97	0.338	1.8

summarizes the results of the deconvolution of Raman spectra to extract G/D peak intensities and area ratios, see Figure 1 and the Supplementary Information for more details. The order of the CF materials in Table 4 is the same as in Table 2. The G peak at about 1580 cm⁻¹ is a common feature of sp²-bonded carbon systems and is found in (partly) graphitic materials. The D peak at about 1360 cm⁻¹ is a feature observed in sp³-bonded carbon systems and indicates disordered or amorphous regions with defects and crystal boundaries [60]. In the literature, both the peak intensity I_G/I_D and the area ratio A_G,BWF/A_D are interpreted as measures of graphitization. The area ratio is more difficult to determine but allows correction for contributions to I_G from a D’ band appearing at about 1620 cm⁻¹.

The data in Table 3 and Table 4 show that the mPitchCFs have significantly higher graphitization and lower porosity than the panCFs with mPitchCF 10 having the highest values of all the CFs studied. Conversely, iPitchCF 12 has the lowest $O_{\mathrm{P}}$, $L_{\mathrm{c}}$, $L_{\mathrm{a}\perp }$ and $L_{\mathrm{a}\Vert }$ values and the highest d₀₀₂ value of all the fibers studied. Its carbonization temperature and duration may have been either low or the isotropic pitch may have only low molecular orientability.

Figure 2 shows examples of cross-sectional SEM-micrographs of some characteristic CF types. The only panCF in this micrograph, panCF 4, shows a granular microstructure typical of panCFs. This is consistent with the small crystallite sizes derived from the XRD-measurements. The isotropic pitchCF 12 in Figure 2 likewise shows a granular structure. The mPitchCFs 10, 11 and 14 show a very different, highly lamellar microstructure. Their high anisotropy is consistent with their significantly higher crystallite dimensions perpendicular ($L_{\mathrm{a}\perp }$) and parallel ($L_{\mathrm{a}\Vert }$) to the fiber axis. Fiber 11 is distinguished by an extremely radial orientation of these lamellae, which was not observed in the other mPitchCF materials. The cross section image of this specimen of mPitchCF 11 in Figure 2 shows a “missing-piece-of-the-cake” defect, sometimes also called a “Pac Man” defect. Such defects are known to form in highly graphitized materials partly already during fiber synthesis as a result of a relaxation of internal stresses due to high fiber volume loss during graphitization. The manufacturer of mPitchCF 14 claimed to use a pitch stirring process during yarn spinning to reduce such defects [61,62]. The lamellae of the mPitchCF 14 sample appear to be less radially oriented than those of the mPitchCF 10 and 11 specimen.

3.2. Fracture Behavior during Ball Milling

Table 5. Morphological characteristics related to the aspect ratio of fiber-shaped fragments after ball milling. Columns denoted by same superscript numbers 1,2 or 3 used a common normalization for their linear scale bars to the maximum of these columns. HARFSs denote HARFOs with diameters less than the initial CF diameter.

Fiber ID	Mean Aspect Ratio 1 of WHOFOs [1]	Mean Aspect Ratio 1 of HARFOs [1]	Mean Length 2 of WHOFOs [µm]	Mean Length 2 of HARFOs [µm]	Mean Length 2 of HARFSs [µm]	Mean Diameter 3 of WHOFOs [µm]	Mean Diameter 3 of HARFOs [µm]	Mean Diameter 3 of HARFSs [µm]
12 iPitch	4.8 ± 1.5	4.2 ± 1.1	10.4 ± 4.9	17.7 ± 12.5	15.9 ± 12.3	2.2 ± 0.7	4.3 ± 3.0	3.6 ± 2.4
1 PAN	4.6 ± 1.6	4.3 ± 1.0	8.8 ± 2.4	7.4 ± 8.6	5.6 ± 4.1	2.0 ± 0.4	1.7 ± 1.6	1.3 ± 1.0
8 PAN	5.0 ± 2.2	4.8 ± 2.1	7.9 ± 2.2	19.3 ± 21.8	10.0 ± 7.5	1.7 ± 0.5	3.7 ± 2.7	2.4 ± 1.7
5 PAN	4.4 ± 1.5	4.6 ± 2.3	7.5 ± 1.1	13.5 ± 15.9	6.1 ± 3.2	1.9 ± 0.7	2.7 ± 1.9	1.6 ± 1.0
4 PAN	4.8 ± 1.4	4.5 ± 1.1	7.6 ± 2.4	9.9 ± 6.4	8.1 ± 5.4	1.7 ± 0.6	2.3 ± 1.6	1.8 ± 1.2
15 PAN	4.3 ± 1.7	4.3 ± 1.2	7.1 ± 1.9	11.6 ± 7.6	5.0 ± 2.5	1.8 ± 0.6	2.8 ± 1.7	1.2 ± 0.8
14 mPitch	5.3 ± 2.9	5.3 ± 2.5	8.0 ± 2.3	6.4 ± 5.9	5.5 ± 3.4	1.7 ± 0.6	1.4 ± 1.5	1.2 ± 0.9
11 mPitch	6.9 ± 4.6	5.7 ± 3.2	8.0 ± 2.0	6.4 ± 5.3	6.1 ± 4.3	1.4 ± 0.6	1.3 ± 1.4	1.2 ± 1.1
10 mPitch	8.2 ± 5.1	7.1 ± 4.3	10.9 ± 5.5	10.5 ± 7.4	10.3 ± 6.6	1.5 ± 0.7	1.8 ± 1.5	1.8 ± 1.3

,

Table 6. Categorization results based on morphological characteristics of fiber-shaped fragments after ball milling. The linear scale bars of the percentages in the columns are normalized to 100%. HARFSs denote HARFOs with diameters below the initial CF diameter (Splinters), HARFCs and LARFCs those with approximately the initial diameter (Chunks).

Fiber ID	LARPCs per Fragments [%]	HARFOs per Fragments [%]	WHOFOs per Fragments [%]	WHOFOs per HARFOs [%]	HARFOs shorter 5 µm per HARFOs [%]	HARFOs thicker 3 µm per HARFOs [%]	HARFSs per HARFOs [%]	HARFCs per HARFOs [%]
12 iPitch	5.5 ± 1.1	5 ± 1	1.0 ± 0.4	20 ± 10	20 ± 10	60 ± 20	88 ± 26	12 ± 7
1 PAN	2.9 ± 0.8	11 ± 2	1.9 ± 0.6	19 ± 6	69 ± 15	13 ± 5	94 ± 18	6 ± 3
8 PAN	6.7 ± 1.2	14 ± 2	3.5 ± 0.9	25 ± 7	25 ± 7	51 ± 11	72 ± 13	30 ± 8
5 PAN	5.5 ± 1.0	12 ± 2	2.8 ± 0.7	25 ± 7	39 ± 9	36 ± 9	70 ± 14	33 ± 8
4 PAN	4.0 ± 0.9	5 ± 1	2.1 ± 0.6	41 ± 15	26 ± 11	33 ± 13	81 ± 23	26 ± 11
15 PAN	10.5 ± 1.5	13 ± 2	2.6 ± 0.7	19 ± 6	30 ± 8	51 ± 11	51 ± 11	49 ± 10
14 mPitch	1.0 ± 0.4	39 ± 3	13.7 ± 1.7	35 ± 5	58 ± 7	6 ± 2	97 ± 10	3 ± 1
11 mPitch	0.9 ± 0.4	47 ± 4	16.3 ± 1.9	35 ± 4	58 ± 6	7 ± 2	99 ± 9	1 ± 1
10 mPitch	0	72 ± 5	41.0 ± 3.4	57 ± 5	26 ± 3	18 ± 2	99 ± 7	1 ± 0

and

Table 7. Measurands for the propensity to form WHOFOs, HARFOs and LARPOs normalized to WHOFO number, milled length or milled volume, respectively. Milled length and volume are influenced by the fiber diameter and the number of filaments, see Table 2.

Fiber ID	Milled Filament Length for 10k WHOFOs [mm/10k]	WHOFOs per Milled Filament Length [1/mm]	HARFOs per Milled Filament Length [1/mm]	WHOFOs per Milled CF Volume [1/pL]	HARFOs per Milled CF Volume [1/pL]	LARPOs per Milled CF Volume [1/pL]	LARPOs+HARFOs per Milled CF Volume [1/pL]
12 iPitch	490 ± 290	20 ± 12	102 ± 44	0.3 ± 0.1	1.3 ± 0.4	26.0 ± 6.5	27.3 ± 6.8
1 PAN	226 ± 113	44 ± 22	239 ± 98	1.1 ± 0.5	6.2 ± 1.7	52.8 ± 13.0	59.0 ± 14.5
8 PAN	632 ± 288	16 ± 7	64 ± 26	0.4 ± 0.1	1.7 ± 0.5	10.0 ± 2.5	11.6 ± 2.9
5 PAN	517 ± 240	19 ± 9	79 ± 32	1.0 ± 0.3	4.0 ± 1.1	30.7 ± 7.6	34.8 ± 8.5
4 PAN	518 ± 254	19 ± 9	47 ± 20	1.0 ± 0.4	2.5 ± 0.8	45.9 ± 11.3	48.4 ± 11.9
15 PAN	969 ± 459	10 ± 5	53 ± 21	0.7 ± 0.2	3.5 ± 0.9	22.9 ± 5.6	26.4 ± 6.4
14 mPitch	24 ± 10	420 ± 168	1200 ± 467	10.9 ± 2.9	31.2 ± 7.7	48.6 ± 11.9	79.8 ± 19.3
11 mPitch	9 ± 3	1152 ± 457	3311 ± 1284	12.1 ± 3.2	34.8 ± 8.6	39.4 ± 9.6	74.2 ± 17.9
10 mPitch	29 ± 11	348 ± 135	614 ± 237	3.7 ± 0.9	6.5 ± 1.6	2.5 ± 0.6	8.9 ± 2.2

present the results of the morphological characteristics obtained from the analysis of the ball-milled fragments. These experimental data include the magnitude of different morphological classes in different metrics, hereafter referred to as ‘observables’. They are used to address the most pressing question of the propensity to form WHO-fibers in the disintegration scenario studied and to study in more detail the fracture modes that occur. The order of the CF materials in these tables is again the same as in the previous tables in order to facilitate visual identification of possible correlations between material properties and observables.

The ratio of WHOFOs or HARFOs per all fragments can be interpreted as the tendency of a CF material to form such objects in the investigated process, whereas 100% minus the HARFO percentage corresponds to the percentage of LARPOs formed.

3.2.1. Fragment Yield in Different Metrices

The morphological data, reported in Table 6 as the relative incidences of different morphological objects, were converted in Table 7 into three different metrics expressing the fragmentation propensities as the resulting number of WHOFOs, HARFOs or LARPOs for a given volume of CF milled, the filament length milled or its reciprocal: the filament length to be milled to a given number of WHOFOs. The normalization of the number of potentially hazardous respirable objects formed to the amount of CF processed relates such numbers to the macro world of CF handling and serves to compare and rank the CF materials studied with respect to their fracture characteristics. Although the fragments were produced under worst-case disintegration conditions in a closed system, they may nevertheless help to estimate upper limits on workplace concentrations and occupational exposure, and to design safety measures for the machining of CF materials, see Section 4.

3.2.2. Wedge-Shaped Fragments

Data on wedge-shaped objects with opening angles greater than 10° are summarized in

Table 8. Statistics for WHOFOs with a wedge-opening-angle (WOA) greater than 10°, both as a percentage and as a numerical ratio to all WHOFOs. The mean WOA and the standard deviation of the diameter variation along a WHOFO relative to the mean diameter are also given.

Fiber ID	WHOFOs ≤10° WOA [%]	WHOFOs ≤10° WOA [1]	Mean WOA [°]	Relative Error of Diameter [%]
12 iPitch	100 ± 76	7/7	1.2 ± 0.6	4.5 ± 1.8
1 PAN	92 ± 52	12/13	3.3 ± 0.9	15.4 ± 2.9
8 PAN	78 ± 39	14/18	5.9 ± 1.4	19.7 ± 2.6
5 PAN	89 ± 42	17/19	4.5 ± 1.1	12.0 ± 2.6
4 PAN	100 ± 63	10/10	1.7 ± 0.9	7.3 ± 3.3
15 PAN	81 ± 43	13/16	5.6 ± 1.8	16.0 ± 4.4
14 mPitch	92 ± 22	68/74	2.6 ± 0.5	8.9 ± 1.3
11 mPitch	97 ± 19	104/107	1.4 ± 0.3	6.3 ± 1.0
10 mPitch	95 ± 13	203/214	2.2 ± 0.2	8.6 ± 0.7

. The standard deviation (relative error) of the diameter along the fragment, the mean wedge angle and the number of WHOFOs with a wedge angle smaller than 10° all follow a similar trend. The data show that typically more than to 80–90% of the WHOFOs had a fiber-like appearance with an opening angle less than 10°. This shows that, again for panCFs, the majority of WHOFOs formed by ball milling were true fiber-like, not wedge-shaped fragments. Furthermore, there is currently no justification to consider wedge-shaped WHO-fibers as fiber-toxicologically irrelevant. Therefore all observed WHOFOs should be recorded and counted. Some examples of wedge-shaped fragments and classical fiber-shaped fragments are shown in

Table 9. Examples of wedge-shaped and fiber-shaped WHOFOs as observed after ball milling. The manual measurement of the fragment is shown as an overlay “segment” (left), the segment has been rectified along its backbone (red) to derive geometry-related data (right).

panCF 8 Wedge-shaped
Arc length: 6.4 µm|Median width: 2.0 µm|Mean width: (1.8 ± 0.7) µm, δ = 39%|Opening angle: 20.2°
panCF 8 Fiber-shaped
Arc length: 8.0 µm|Median width: 1.8 µm|Mean width: (1.7 ± 0.2) µm, δ = 13%|Opening angle: 3.5°
panCF 5 Wedge-shaped
Arc length: 7.7 µm|Median width: 2.0 µm|Mean width: (1.9 ± 0.8) µm, δ = 44%|Opening angle: 16.1°
panCF 5 Fiber-shaped
Arc length: 6.2 µm|Median width: 1.1 µm|Mean width: (1.0 ± 0.1) µm, δ = 14%|Opening angle: 4.1°
mPitchCF 14 Wedge-shaped
Arc length: 10.4 µm|Median width: 3.3 µm|Mean width: (2.6 ± 0.8) µm, δ = 32%|Opening angle: 13.9°
mPitchCF 14 Fiber-shaped
Arc length: 10.4 µm|Median width: 0.5 µm|Mean width: (0.5 ± 0.1) µm, δ = 17%|Opening angle: 0.1°

.

3.3. Visualization of Material Parameters and Fragment Characteristics

Selected material parameters and observed fragment characteristics are plotted on radial axes in Figure 3. The right plot helps to visually identify further differences between panCFs and pitchCFs: Unlike mPitchCFs, panCFs are confined to a V-shaped pattern of the radial plot. The left plot shows that panCFs 4, 5 and 8 (bluish colors) are very similar with respect to many features, whereas panCF 1 (black) and iPitchCF 15 (green) show significant deviations, with panCF 1 having the highest propensity of all panCFs to form WHO-fragments.

4. Discussion

The following sections discuss material-specific findings that lead to a proposal for grouping and ranking of CF materials. The study of correlations between observed fragmentation characteristics and material properties of the CFs aims to identify critical material properties that promote the formation of respirable fiber fragments.

4.1. Material Grouping Based on the Mean Diameter of High-Aspect Ratio Fragments

For the preceding presentation of results and the following discussion, the data in Table 5 and Table 6, and in particular the individual diameter-versus-length scatter plots in the Supplementary Information suggest that the investigated CF materials can be divided into two separate groups with respect to their fragmentation behavior:

• “LDH” (Lower mean Diameter HARFO) materials, including panCF 1 and mPitchCFs 10, 11, 14 which formed HARFOs with mean diameters below 2.0 µm
• “HDH” (Higher mean Diameter HARFO) materials, including panCFs 4, 5, 8, 15 and iPitchCF 12 which formed HARFOs with mean diameters greater than 2.0 µm.

When comparing the LDH materials panCF 1, mPitchCF 10, 11 and 14 with the HDH materials panCF 4, 5, 8 and iPitchCF 12, the following fragmentation characteristics are notable, see also Figure 4 and Figure 5.

• With respect to diameter

  ○

  Compared to the HDH materials, the LDH materials formed fewer HARFCs per HARFOs ((3 ± 1)% vs. (26 ± 4)%), i.e., “chunk” HARFOs of approximately the initial CF diameter.

  ○

  Therefore, not only the HARFOs but also the HARFSs, i.e., “splinter” HARFOs with diameters below the initial diameter, tended to be thinner for LDH than for HDH materials ((1.3 ± 0.5) µm vs. (2.0 ± 0.7) µm).

  ○

  This resulted in a significantly lower percentage of HARFOs thicker than 3 µm and HARFCs for the LDH materials than for the HDH materials ((9 ± 2)% vs. (44 ± 6)%).

  ○

  Naturally, the mean HARFO diameter of the LDH materials was lower than that of the HDH materials ((1.5 ± 0.8) µm vs. (3.0 ± 1.0) µm), as this observable was used to define the two groups of materials.

• In terms of length

  ○

  The HARFOs formed from the LDH materials were on average not only thinner than the HDH materials but also showed a tendency to be shorter ((7 ± 4) µm vs. (13 ± 5) µm), except for mPitchCF 10, see Section 4.4.

Figure 4 analyzes the data underlying Table 5 for six morphological classes: HARFOs, HARFSs, WHOFOs, HARFCs and HARFOs that are either too short or too thick to be a WHOFO. All individual HARFO diameters, normalized to the initial CF diameter, are plotted against the HARFO length data. This allows the diameter reduction of materials with different initial diameters to be directly compared. However, the vertical error bars shown do not include the uncertainty in the initial diameter but the normalized standard deviation. Individual plots for the nine CF materials can be found in the Supplementary Information. Images of fragments with diameters significantly larger than the initial CF diameter were examined. They were found to consist of densely-packed agglomerates that could not be disentangled and were counted as a single object.

As described above, a mean HARFO diameter greater than 2 µm was to assign materials to the HDH group. Figure 4 visualizes that all HDH fractions contribute to this larger diameter: A significantly larger percentage (30%) of HDH materials retained their initial CF diameter (HARFC, grey) than LDH materials (2%). Also the WHOFOs (red), HARFOs too thick (purple) and too short (blue) to be WHOFOs were systematically thicker for HDH material. These different fragmentation characteristics can be seen by fitting log-normal distributions to the histograms of the normalized diameter values in the left plot of Figure 5. The distribution of the HARFC diameters has a mean value of (101 ± 16)%, i.e., a relative error of 16%. Consequently, since thicker fibers break less easily, the mean HARFO (black) length of the HDH group was approximately twice that of the LDH HARFOs. With regard to the group-averaged WHOFO (red) lengths however, both mean lengths were similar: (8.1 ± 1.3) µm and (8.4 ± 1.3) µm. However, there is a significant separation between those HARFOs that are too short to be WHOFOs and the WHOFO fraction on the one hand, and those HARFOs that are too thick to be WHOFOs, i.e., HARFCs, and the other HARFOs, i.e., HARFSs, on the other hand, resulting in two peaks of the length distribution in the right plot of Figure 5.

The WHO limit on diameter also appears to limit the WHOFO length resulting from ball milling. The mechanical properties of a CF material appear to have only a minor effect on the resulting aspect ratio, see Section 4.3.1.

4.2. Material- and Group-Specific Findings

Table 6 shows on a relative scale that the three mPitchCFs of the LDH material group formed significantly more WHOFOs relative to all fragments compared to all other CF material, including panCF 1. Whereas in Table 7, at least on the scale of WHOFOs per milled filament length, all four LDH materials showed a higher propensity to form WHOFOs than the HDH material. However, this trend was not significant for panCF 1 on the scale of WHOFOs formed per milled volume.

For same machined filament length, thinner CFs carry less volume. A length-related metric thus emphasizes possible effects of the initial diameter of a CF material. However, for polymer reinforcement, the added CF volume or mass can generally be considered more relevant than the incorporated CF length. The excess of WHOFO formation of panCF 1 that was observed with the machined filament length metric may therefore not be of practical relevance for machining CFRP.

It is however important to note that, with respect to WHOFO formation, the ratio of the least critical mPitchCF 10 to the most critical non-mPitchCF, namely panCF 1, is just (3.7 ± 0.9)/(1.1 + 0.5) = (3.2 ± 1.5) with respect to milled pL CF and (1664 ± 395)/(650 ± 253) = (2.6 ± 1.2) with respect to milled µg CF mass and (348 ± 135)/(44 ± 22) = (8 ± 5) with respect to milled mm CF filament length, cf. Table 7.

For the averaged numbers of WHOFOs formed from all mPitch and all non-mPitch CFs, these ratios were (11 ± 2)/(0.9 ± 0.2) = (12.7 ± 3.4) with respect to milled pL CF and (5231 ± 922)/(487 ± 95) = (11 ± 3) with respect to milled µg CF mass and (7400 ± 2200)/(253 ± 71) = (29 ± 12) with respect to milled cm CF filament length.

Notable material-specific findings include

• The panCF 1, being a very commonly-used fiber with standard material properties, disintegrated into—on average—thinner HARFOs than the other panCFs. In this respect its fragmentation characteristics were more similar to mPitchCFs than to the other panCFs, which motivated to the formation of the LDH group of materials. As the mean diameter of the HARFSs formed was not significantly thinner than that of the other panCFs, the smaller mean HARFO diameter of panCF 1 was due to the lower percentage of HARFCs formed.
• PanCF 1 was the highest-ranking panCF in terms of HARFOs and WHOFOs per milled length. In terms of this metric, it differed significantly from panCF 8, which has the same initial diameter and quite similar material properties. PanCF 5, 4 and 15 are materials with a smaller initial diameter and require a greater length to be milled for the same volume. As a result, the distance of panCF 1 to 4, 5 and 15 is smaller when normalized to volume.
• Although panCF 8 is very similar to panCF 1 in terms of material properties, their fragmentation characteristics were significantly different, particularly in terms of the mean length and diameter of the HARFOs and the percentage of HARFOs that were too short or too thick to form WHOFOs.
• However, when compared to mPitchCF, the propensity of panCF 1 to form HARFOs and WHOFOs was only (11 ± 2)%/(44 ± 3)% = (24 ± 4)% and (1.9 ± 0.6)%/(16.3 ± 1.2)% = (12 ± 4)%, respectively, indicating that pan CF 1 formed far more LARPOs.
• The isotropic pitchCF 12, with material properties similar to those of panCFs, showed a disintegration behavior similar to panCFs in all aspects.

4.3. Correlations between Fragmentation Characteristics and Material Properties

In the following section we try to extract useful information about possible correlations between the fragmentation behavior of a CF material during ball milling and its material properties. Both Pearson correlation (PC) and ${\chi }^2$-tests were performed to search for statistically and experimentally significant relationships.

4.3.1. Testing of Normality, Linear Indepence and Goodness-of-Fit

Pearson correlation analysis tests the null hypothesis that two selected datasets are linearly independent, and the alternative hypothesis that they are not. Low resulting $p_{\mathrm{P}\mathrm{C}}$-values support the alternative hypothesis of linear dependence. To provide valid estimates of the statistical significance of such a linear independence, the test requires the data to be normally distributed. Selected material property and fragmentation characteristic datasets were therefore first subjected to a Kolmogorov-Smirnov (KS) test. KS performs a goodness-of-fit test with the null hypothesis that the dataset is drawn from a population with a normal distribution with the mean value and standard deviation of the dataset. High $p_{\mathrm{K}\mathrm{S}}$-values support the normality hypothesis.

However, as the ensemble of only nine materials from three very different precursor groups is rather small and diverse, these KS and PC analyzes must be considered as not very strong. An analysis of the responsibility of each fiber type for a deviation from normality can be found in the Supplementary Information.

KS test results for observed fragmentation characteristics (“observables”) and material properties are reported in the following

Table 10. Results of the-values of Kolmogorov-Smirnov (KS) normality tests and of Pearson Correlation (PC) tests for linear independence on the interlayer distance d₀₀₂ for selected material properties before and after applying a parameter transformation, see text. For the property grouping P1–P5, see Section 4.3.2.

Property Group	Original Material Property	Transformed Property of Improved Normality and Linear Dependence to ϱ	Original pKS-Value	Transformed pKS-Value	Original pPC-Value to ϱ	Transformed pPC-Value to ϱ
P1	Microporosity $P_{\mu }$		0.43		0.000
	Density $\varrho$		0.47		0.000
P2	Partial Orientation $O_{\mathrm{P}}$		0.69		0.007
P3	Interlayer Spacing $d_{002}$		0.99		0.003
	Tensile Modulus $E_{\mathrm{L}}$		0.98		0.000
	Crystallite Size $L_{a\perp }$	$\mathrm{l}\mathrm{o}\mathrm{g}\left(L_{a\perp }\right)$	0.40	0.69	0.006	0.000
	Crystallite Size $L_{a\left|\right|}$	$\mathrm{l}\mathrm{o}\mathrm{g}\left(L_{a\left|\right|}\right)$	0.51	0.59	0.000	0.000
	Thermal Conductivity $q_{\mathrm{T}}$	${\mathrm{l}\mathrm{o}\mathrm{g}(q}_{\mathrm{T}})$	0.09	0.96	0.028	0.000
	Raman Area Ratio $A_{\mathrm{G}}/A_{\mathrm{D}}$	log(AG/AD)	0.28	0.30	0.011	0.001
	Elongation at Break ${\epsilon }_{\mathrm{B}}$		0.73		0.001
P4	Tensile Strength ${\sigma }_{\mathrm{T}}$		0.54		0.924
P5	Initial Diameter $d_{\mathrm{i}}$		0.60		0.230

and

Table 11. Results of the p_KS-values of Kolmogorov-Smirnov (KS) normality tests for selected observables (first column). Pearson correlation (PC) and χ²-test results for selected observed fragment properties of the studied CFs (following columns). The 3rd and 4th columns give the results for the standard errors of the WHOFOs and HARFOs counts per volume, while the 5rd and 6th give the results for datasets where the relative errors of the counts of the mPitch 11 and 14 materials were set to 100% to reduce their χ²-fitting weight and where removed from the PC-test, see text. A small p_PC-value in the first row indicates that linear independence is unlikely. The sign indicates the slope of the correlation. A high χ²-probability of the linear fit results when it stays within the estimated experimental errors. A small relative error δb indicates that the slope of the linear fit is reliable. The color coding starts to change from green to cyan to blue for p_PC-values > 0.05 and from green to orange to red for P_ndf(χ²) < 5% or δb > 100% with RGB color mixing.

	${\mathit{p}}_{\mathbf{K}\mathbf{S}}$-Value		WHOFOs per Milled CF Volume		HARFOs per Milled CF Volume		*WHOFOs 11,14 per Milled CF Volume		*HARFOs11,14 per Milled CF Volume		Mean Length of WHOFOs		Mean Length of HARFOs		Mean Aspect Ratio of WHOFOs		Mean Aspect Ratio of HARFOs		Mean Diameter of WHOFOs		Mean Diameter of HARFOs		WHOFOs per HARFOs
WHOFOs per Milled CF Volume				$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.047	$p_{\mathrm{P}\mathrm{C}}$	−0.836	$p_{\mathrm{P}\mathrm{C}}$	−0.046	$p_{\mathrm{P}\mathrm{C}}$	+0.177	$p_{\mathrm{P}\mathrm{C}}$	+0.177	$p_{\mathrm{P}\mathrm{C}}$	−0.094	$p_{\mathrm{P}\mathrm{C}}$	−0.038	$p_{\mathrm{P}\mathrm{C}}$	+0.324
	0.16			$P_{{\chi }^2}$	68%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	69%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	0%
				$\delta b$	21%	$\delta b$	28%	$\delta b$	31%	$\delta b$	>199%	$\delta b$	113%	$\delta b$	>199%	$\delta b$	173%	$\delta b$	161%	$\delta b$	105%	$\delta b$	29%
HARFOs per Milled CF Volume		$p_{\mathrm{P}\mathrm{C}}$	+0.000			$p_{\mathrm{P}\mathrm{C}}$	+0.047	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.677	$p_{\mathrm{P}\mathrm{C}}$	−0.041	$p_{\mathrm{P}\mathrm{C}}$	+0.306	$p_{\mathrm{P}\mathrm{C}}$	+0.313	$p_{\mathrm{P}\mathrm{C}}$	−0.144	$p_{\mathrm{P}\mathrm{C}}$	−0.042	$p_{\mathrm{P}\mathrm{C}}$	+0.522
	0.10	$P_{{\chi }^2}$	68%			$P_{{\chi }^2}$	68%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	0%
		$\delta b$	21%			$\delta b$	30%	$\delta b$	27%	$\delta b$	>199%	$\delta b$	111%	$\delta b$	>199%	$\delta b$	197%	$\delta b$	184%	$\delta b$	106%	$\delta b$	80%
*WHOFOs11,14 per Milled CF Volume		$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.047			$p_{\mathrm{P}\mathrm{C}}$	+0.047	$p_{\mathrm{P}\mathrm{C}}$	+0.197	$p_{\mathrm{P}\mathrm{C}}$	−0.283	$p_{\mathrm{P}\mathrm{C}}$	+0.003	$p_{\mathrm{P}\mathrm{C}}$	+0.002	$p_{\mathrm{P}\mathrm{C}}$	−0.159	$p_{\mathrm{P}\mathrm{C}}$	−0.104	$p_{\mathrm{P}\mathrm{C}}$	+0.014
	0.16	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	68%			$P_{{\chi }^2}$	69%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	74%
		$\delta b$	28%	$\delta b$	30%			$\delta b$	32%	$\delta b$	>199%	$\delta b$	137%	$\delta b$	>199%	$\delta b$	188%	$\delta b$	172%	$\delta b$	132%	$\delta b$	32%
*HARFOs11,14 per Milled CF Volume		$p_{\mathrm{P}\mathrm{C}}$	+0.047	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.047			$p_{\mathrm{P}\mathrm{C}}$	+0.544	$p_{\mathrm{P}\mathrm{C}}$	−0.043	$p_{\mathrm{P}\mathrm{C}}$	+0.233	$p_{\mathrm{P}\mathrm{C}}$	+0.195	$p_{\mathrm{P}\mathrm{C}}$	−0.522	$p_{\mathrm{P}\mathrm{C}}$	−0.008	$p_{\mathrm{P}\mathrm{C}}$	+0.398
	0.10	$P_{{\chi }^2}$	69%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	69%			$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	13%
		$\delta b$	31%	$\delta b$	27%	$\delta b$	32%			$\delta b$	>199%	$\delta b$	138%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	192%	$\delta b$	136%	$\delta b$	33%
Mean Length of WHOFOs		$p_{\mathrm{P}\mathrm{C}}$	−0.836	$p_{\mathrm{P}\mathrm{C}}$	−0.677	$p_{\mathrm{P}\mathrm{C}}$	+0.197	$p_{\mathrm{P}\mathrm{C}}$	+0.544			$p_{\mathrm{P}\mathrm{C}}$	+0.692	$p_{\mathrm{P}\mathrm{C}}$	+0.110	$p_{\mathrm{P}\mathrm{C}}$	+0.193	$p_{\mathrm{P}\mathrm{C}}$	+0.563	$p_{\mathrm{P}\mathrm{C}}$	+0.748	$p_{\mathrm{P}\mathrm{C}}$	+0.315
	0.32	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%			$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%
		$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%			$\delta b$	>199%	$\delta b$	185%	$\delta b$	>199%	$\delta b$	175%	$\delta b$	>199%	$\delta b$	>199%
Mean Length of HARFOs		$p_{\mathrm{P}\mathrm{C}}$	−0.046	$p_{\mathrm{P}\mathrm{C}}$	−0.041	$p_{\mathrm{P}\mathrm{C}}$	−0.283	$p_{\mathrm{P}\mathrm{C}}$	−0.043	$p_{\mathrm{P}\mathrm{C}}$	+0.692			$p_{\mathrm{P}\mathrm{C}}$	−0.442	$p_{\mathrm{P}\mathrm{C}}$	−0.419	$p_{\mathrm{P}\mathrm{C}}$	+0.245	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.369
	0.97	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%			$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%
		$\delta b$	113%	$\delta b$	111%	$\delta b$	137%	$\delta b$	138%	$\delta b$	>199%			$\delta b$	>199%	$\delta b$	>199%	$\delta b$	151%	$\delta b$	117%	$\delta b$	>199%
Mean Aspect Ratio of WHOFOs		$p_{\mathrm{P}\mathrm{C}}$	+0.177	$p_{\mathrm{P}\mathrm{C}}$	+0.306	$p_{\mathrm{P}\mathrm{C}}$	+0.003	$p_{\mathrm{P}\mathrm{C}}$	+0.233	$p_{\mathrm{P}\mathrm{C}}$	+0.110	$p_{\mathrm{P}\mathrm{C}}$	−0.442			$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.055	$p_{\mathrm{P}\mathrm{C}}$	−0.222	$p_{\mathrm{P}\mathrm{C}}$	+0.006
	0.29	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%			$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%
		$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	185%	$\delta b$	>199%			$\delta b$	166%	$\delta b$	172%	$\delta b$	>199%	$\delta b$	195%
Mean Aspect Ratio of HARFOs		$p_{\mathrm{P}\mathrm{C}}$	+0.177	$p_{\mathrm{P}\mathrm{C}}$	+0.313	$p_{\mathrm{P}\mathrm{C}}$	+0.002	$p_{\mathrm{P}\mathrm{C}}$	+0.195	$p_{\mathrm{P}\mathrm{C}}$	+0.193	$p_{\mathrm{P}\mathrm{C}}$	−0.419	$p_{\mathrm{P}\mathrm{C}}$	+0.000			$p_{\mathrm{P}\mathrm{C}}$	−0.038	$p_{\mathrm{P}\mathrm{C}}$	−0.169	$p_{\mathrm{P}\mathrm{C}}$	+0.002
	0.58	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%			$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%
		$\delta b$	173%	$\delta b$	197%	$\delta b$	188%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	166%			$\delta b$	181%	$\delta b$	>199%	$\delta b$	178%
Mean Diameter of WHOFOs		$p_{\mathrm{P}\mathrm{C}}$	−0.094	$p_{\mathrm{P}\mathrm{C}}$	−0.144	$p_{\mathrm{P}\mathrm{C}}$	−0.159	$p_{\mathrm{P}\mathrm{C}}$	−0.522	$p_{\mathrm{P}\mathrm{C}}$	+0.563	$p_{\mathrm{P}\mathrm{C}}$	+0.245	$p_{\mathrm{P}\mathrm{C}}$	−0.055	$p_{\mathrm{P}\mathrm{C}}$	−0.038			$p_{\mathrm{P}\mathrm{C}}$	+0.089	$p_{\mathrm{P}\mathrm{C}}$	−0.044
	0.98	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%			$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%
		$\delta b$	161%	$\delta b$	184%	$\delta b$	172%	$\delta b$	192%	$\delta b$	175%	$\delta b$	151%	$\delta b$	172%	$\delta b$	181%			$\delta b$	148%	$\delta b$	132%
Mean Diameter of HARFOs		$p_{\mathrm{P}\mathrm{C}}$	−0.038	$p_{\mathrm{P}\mathrm{C}}$	−0.042	$p_{\mathrm{P}\mathrm{C}}$	−0.104	$p_{\mathrm{P}\mathrm{C}}$	−0.008	$p_{\mathrm{P}\mathrm{C}}$	+0.748	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.222	$p_{\mathrm{P}\mathrm{C}}$	−0.169	$p_{\mathrm{P}\mathrm{C}}$	+0.089			$p_{\mathrm{P}\mathrm{C}}$	−0.193
	0.91	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%			$P_{{\chi }^2}$	98%
		$\delta b$	105%	$\delta b$	106%	$\delta b$	132%	$\delta b$	136%	$\delta b$	>199%	$\delta b$	117%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	148%			$\delta b$	187%
WHOFOs per HARFOs		$p_{\mathrm{P}\mathrm{C}}$	+0.324	$p_{\mathrm{P}\mathrm{C}}$	+0.522	$p_{\mathrm{P}\mathrm{C}}$	+0.014	$p_{\mathrm{P}\mathrm{C}}$	+0.398	$p_{\mathrm{P}\mathrm{C}}$	+0.315	$p_{\mathrm{P}\mathrm{C}}$	−0.369	$p_{\mathrm{P}\mathrm{C}}$	+0.006	$p_{\mathrm{P}\mathrm{C}}$	+0.002	$p_{\mathrm{P}\mathrm{C}}$	−0.044	$p_{\mathrm{P}\mathrm{C}}$	−0.193
	0.63	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	74%	$P_{{\chi }^2}$	13%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	98%
		$\delta b$	29%	$\delta b$	31%	$\delta b$	32%	$\delta b$	33%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	195%	$\delta b$	178%	$\delta b$	132%	$\delta b$	187%

*WHOFO^11,14 and *HARFO^11,14 denote datasets where the relative errors of the counts of the mPitch 11 and 14 materials were set to 100% to reduce their χ²-fitting weight and where removed from the PC-test, see text.

, respectively.

In addition to the PC tests, χ²-goodness-of-fit tests were performed by fitting a linear function y = a + b·x to data pairs using the error-weighted approach of York et al. that account for both x- and y-errors [63]. This allows the hypothesis of a linear functional dependence to be tested in relation to the magnitude of the measurement errors.

The resulting error-weighted sum of residuals (χ²$)$ was subjected to a ${\chi }^2$-test. A linear fit with offset $a$ and slope $b$ consumes with its 2 parameters 2 of the 9 degrees-of-freedom (ndf) provided by the 9 CF materials studied: ndf = 9 – 2 = 7. If the ${\chi }^2$-probability value P_ndf(χ²) falls below a significance level of α = 0.05, the hypothesis of a linear correlation will be rejected. A significance level of α = 0.05 was chosen for the coloring of Table 11,

Table 12. χ²-probability for the sum-of-residua normalized to ndf = 7 degrees-of-freedom.

ndf = 7: χ2/ndf	0.00	0.12	0.18	0.30	0.40	0.55	0.69	0.91	1.00	1.40	1.72	2.01	2.64	3.47	4.27
Pndf(χ2) [%]	100.00	99.73	99.00	95.45	90.00	80.00	68.27	50.00	42.89	20.00	10.00	5.00	1.00	0.10	0.01

,

Table 13. Pearson correlation (PC) and χ² test results for selected material properties of the CFs studied: A small p_PC-value in the first row indicates that linear independence is unlikely. The sign indicates the slope of the correlation. A high χ²-probability of the linear fit results when it stays within the estimated experimental errors. A small relative error δb indicates that the slope of the linear fit is reliable. The color coding starts to change from green to cyan to blue for p_PC-values > 0.05 and from green to orange to red for P_ndf (χ²) < 5% or δb > 100% with RGB color mixing.

		P1				P2		P4														P4		P5
Property Group		Microporosity ${\mathit{P}}_{\mathit{\mu }}$		Specific Density $\mathit{\varrho }$		Partial Orientation ${\mathit{O}}_{\mathbf{P}}$		Interlayer Spacing ${\mathit{d}}_{002}$		Tensile Modulus ${\mathit{E}}_{\mathbf{L}}$		Crystallite Size ${\mathbf{l}\mathbf{o}\mathbf{g}(\mathit{L}}_{\mathit{a}\perp })$		Crystallite Size ${\mathbf{l}\mathbf{o}\mathbf{g}(\mathit{L}}_{\mathit{a}\left|\right|})$		Thermal Conductivity ${\mathbf{l}\mathbf{o}\mathbf{g}(\mathit{q}}_{\mathbf{T}})$		Raman Area Ratio $\mathbf{l}\mathbf{o}\mathbf{g}({\mathit{A}}_{\mathbf{G}}/{\mathit{A}}_{\mathbf{D}})$		Elongation at Break ${\mathit{\epsilon }}_{\mathbf{B}}$		Tensile Strength ${\mathit{\sigma }}_{\mathbf{T}}$		Initial CF Diameter ${\mathit{d}}_{\mathbf{i}}$
P1	Micro- porosity $P_{\mu }$			$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.010	$p_{\mathrm{P}\mathrm{C}}$	+0.006	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.002	$p_{\mathrm{P}\mathrm{C}}$	+0.873	$p_{\mathrm{P}\mathrm{C}}$	−0.193
				$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	84%	$P_{{\chi }^2}$	94%	$P_{{\chi }^2}$	97%	$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	96%	$P_{{\chi }^2}$	95%	$P_{{\chi }^2}$	95%	$P_{{\chi }^2}$	17%	$P_{{\chi }^2}$	41%
				$\delta b$	41%	$\delta b$	38%	$\delta b$	41%	$\delta b$	35%	$\delta b$	35%	$\delta b$	33%	$\delta b$	36%	$\delta b$	35%	$\delta b$	36%	$\delta b$	>199%	$\delta b$	53%
	Specific Density $\varrho$	$p_{\mathrm{P}\mathrm{C}}$	+0.000			$p_{\mathrm{P}\mathrm{C}}$	+0.007	$p_{\mathrm{P}\mathrm{C}}$	−0.003	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	−0.924	$p_{\mathrm{P}\mathrm{C}}$	+0.230
		$P_{{\chi }^2}$	100%			$P_{{\chi }^2}$	79%	$P_{{\chi }^2}$	95%	$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	96%	$P_{{\chi }^2}$	94%	$P_{{\chi }^2}$	95%	$P_{{\chi }^2}$	6%	$P_{{\chi }^2}$	21%
		$\delta b$	41%			$\delta b$	33%	$\delta b$	37%	$\delta b$	31%	$\delta b$	30%	$\delta b$	29%	$\delta b$	31%	$\delta b$	30%	$\delta b$	32%	$\delta b$	>199%	$\delta b$	47%
P2	Partial Orientation $O_{\mathrm{P}}$	$p_{\mathrm{P}\mathrm{C}}$	−0.010	$p_{\mathrm{P}\mathrm{C}}$	+0.007			$p_{\mathrm{P}\mathrm{C}}$	−0.002	$p_{\mathrm{P}\mathrm{C}}$	+0.003	$p_{\mathrm{P}\mathrm{C}}$	+0.009	$p_{\mathrm{P}\mathrm{C}}$	+0.011	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.040	$p_{\mathrm{P}\mathrm{C}}$	−0.008	$p_{\mathrm{P}\mathrm{C}}$	+0.240	$p_{\mathrm{P}\mathrm{C}}$	−0.838
		$P_{{\chi }^2}$	84%	$P_{{\chi }^2}$	79%			$P_{{\chi }^2}$	82%	$P_{{\chi }^2}$	7%	$P_{{\chi }^2}$	5%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	30%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	6%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%
		$\delta b$	38%	$\delta b$	33%			$\delta b$	26%	$\delta b$	14%	$\delta b$	15%	$\delta b$	14%	$\delta b$	15%	$\delta b$	15%	$\delta b$	17%	$\delta b$	15%	$\delta b$	31%
P3	Interlayer Spacing $d_{002}$	$p_{\mathrm{P}\mathrm{C}}$	+0.006	$p_{\mathrm{P}\mathrm{C}}$	−0.003	$p_{\mathrm{P}\mathrm{C}}$	−0.002			$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	−0.640	$p_{\mathrm{P}\mathrm{C}}$	−0.795
		$P_{{\chi }^2}$	94%	$P_{{\chi }^2}$	95%	$P_{{\chi }^2}$	82%			$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	97%	$P_{{\chi }^2}$	82%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	79%	$P_{{\chi }^2}$	86%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	1%
		$\delta b$	41%	$\delta b$	37%	$\delta b$	26%			$\delta b$	25%	$\delta b$	25%	$\delta b$	26%	$\delta b$	25%	$\delta b$	25%	$\delta b$	27%	$\delta b$	92%	$\delta b$	89%
	Tensile Modulus $E_{\mathrm{L}}$	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.003	$p_{\mathrm{P}\mathrm{C}}$	+0.000			$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.821	$p_{\mathrm{P}\mathrm{C}}$	+0.392
		$P_{{\chi }^2}$	97%	$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	7%	$P_{{\chi }^2}$	99%			$P_{{\chi }^2}$	75%	$P_{{\chi }^2}$	22%	$P_{{\chi }^2}$	97%	$P_{{\chi }^2}$	2%	$P_{{\chi }^2}$	35%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%
		$\delta b$	35%	$\delta b$	31%	$\delta b$	14%	$\delta b$	25%			$\delta b$	15%	$\delta b$	14%	$\delta b$	14%	$\delta b$	11%	$\delta b$	17%	$\delta b$	18%	$\delta b$	64%
	Crystallite Size ${\mathrm{l}\mathrm{o}\mathrm{g}(L}_{a\perp })$	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.009	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000			$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.871	$p_{\mathrm{P}\mathrm{C}}$	+0.340
		$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	5%	$P_{{\chi }^2}$	97%	$P_{{\chi }^2}$	75%			$P_{{\chi }^2}$	20%	$P_{{\chi }^2}$	42%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	70%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%
		$\delta b$	35%	$\delta b$	30%	$\delta b$	15%	$\delta b$	25%	$\delta b$	15%			$\delta b$	12%	$\delta b$	11%	$\delta b$	9%	$\delta b$	16%	$\delta b$	18%	$\delta b$	64%
	Crystallite Size ${\mathrm{l}\mathrm{o}g(L}_{a\left|\right|})$	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.011	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000			$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.707	$p_{\mathrm{P}\mathrm{C}}$	+0.283
		$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	82%	$P_{{\chi }^2}$	22%	$P_{{\chi }^2}$	20%			$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	86%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%
		$\delta b$	33%	$\delta b$	29%	$\delta b$	14%	$\delta b$	26%	$\delta b$	14%	$\delta b$	12%			$\delta b$	11%	$\delta b$	10%	$\delta b$	16%	$\delta b$	17%	$\delta b$	55%
	Thermal Conductivity ${\mathrm{l}\mathrm{o}\mathrm{g}(q}_{\mathrm{T}})$	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.001			$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	−0.003	$p_{\mathrm{P}\mathrm{C}}$	+0.590	$p_{\mathrm{P}\mathrm{C}}$	+0.567
		$P_{{\chi }^2}$	96%	$P_{{\chi }^2}$	96%	$P_{{\chi }^2}$	30%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	97%	$P_{{\chi }^2}$	42%	$P_{{\chi }^2}$	0%			$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	6%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%
		$\delta b$	36%	$\delta b$	31%	$\delta b$	15%	$\delta b$	25%	$\delta b$	14%	$\delta b$	11%	$\delta b$	11%			$\delta b$	6%	$\delta b$	16%	$\delta b$	17%	$\delta b$	>199%
	Raman Area Ratio $\mathrm{l}\mathrm{o}\mathrm{g}(A_{\mathrm{G}}/A_{\mathrm{D}})$	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.040	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.001			$p_{\mathrm{P}\mathrm{C}}$	−0.003	$p_{\mathrm{P}\mathrm{C}}$	−0.718	$p_{\mathrm{P}\mathrm{C}}$	+0.221
		$P_{{\chi }^2}$	95%	$P_{{\chi }^2}$	94%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	79%	$P_{{\chi }^2}$	2%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	1%			$P_{{\chi }^2}$	3%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%
		$\delta b$	35%	$\delta b$	30%	$\delta b$	15%	$\delta b$	25%	$\delta b$	11%	$\delta b$	9%	$\delta b$	10%	$\delta b$	6%			$\delta b$	15%	$\delta b$	113%	$\delta b$	85%
	Elongation at Break ${\epsilon }_{\mathrm{B}}$	$p_{\mathrm{P}\mathrm{C}}$	+0.002	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	−0.008	$p_{\mathrm{P}\mathrm{C}}$	+0.001	$p_{\mathrm{P}\mathrm{C}}$	−0.001	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	+0.000	$p_{\mathrm{P}\mathrm{C}}$	−0.003	$p_{\mathrm{P}\mathrm{C}}$	−0.003			$p_{\mathrm{P}\mathrm{C}}$	+0.696	$p_{\mathrm{P}\mathrm{C}}$	−0.432
		$P_{{\chi }^2}$	95%	$P_{{\chi }^2}$	95%	$P_{{\chi }^2}$	6%	$P_{{\chi }^2}$	86%	$P_{{\chi }^2}$	35%	$P_{{\chi }^2}$	70%	$P_{{\chi }^2}$	86%	$P_{{\chi }^2}$	6%	$P_{{\chi }^2}$	3%			$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%
		$\delta b$	36%	$\delta b$	32%	$\delta b$	17%	$\delta b$	27%	$\delta b$	17%	$\delta b$	16%	$\delta b$	16%	$\delta b$	16%	$\delta b$	15%			$\delta b$	38%	$\delta b$	102%
P4	Tensile Strength ${\sigma }_{\mathrm{T}}$	$p_{\mathrm{P}\mathrm{C}}$	+0.873	$p_{\mathrm{P}\mathrm{C}}$	−0.924	$p_{\mathrm{P}\mathrm{C}}$	+0.240	$p_{\mathrm{P}\mathrm{C}}$	−0.640	$p_{\mathrm{P}\mathrm{C}}$	+0.821	$p_{\mathrm{P}\mathrm{C}}$	−0.871	$p_{\mathrm{P}\mathrm{C}}$	−0.707	$p_{\mathrm{P}\mathrm{C}}$	+0.590	$p_{\mathrm{P}\mathrm{C}}$	−0.718	$p_{\mathrm{P}\mathrm{C}}$	+0.696			$p_{\mathrm{P}\mathrm{C}}$	−0.035
		$P_{{\chi }^2}$	17%	$P_{{\chi }^2}$	6%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%			$P_{{\chi }^2}$	3%
		$\delta b$	>199%	$\delta b$	>199%	$\delta b$	15%	$\delta b$	92%	$\delta b$	18%	$\delta b$	20%	$\delta b$	23%	$\delta b$	19%	$\delta b$	113%	$\delta b$	38%			$\delta b$	22%
P5	Initial Diameter $d_{\mathrm{i}}$	$p_{\mathrm{P}\mathrm{C}}$	−0.193	$p_{\mathrm{P}\mathrm{C}}$	+0.230	$p_{\mathrm{P}\mathrm{C}}$	−0.838	$p_{\mathrm{P}\mathrm{C}}$	−0.795	$p_{\mathrm{P}\mathrm{C}}$	+0.392	$p_{\mathrm{P}\mathrm{C}}$	+0.340	$p_{\mathrm{P}\mathrm{C}}$	+0.283	$p_{\mathrm{P}\mathrm{C}}$	+0.567	$p_{\mathrm{P}\mathrm{C}}$	+0.221	$p_{\mathrm{P}\mathrm{C}}$	−0.432	$p_{\mathrm{P}\mathrm{C}}$	−0.035
		$P_{{\chi }^2}$	41%	$P_{{\chi }^2}$	21%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	3%
		$\delta b$	53%	$\delta b$	47%	$\delta b$	31%	$\delta b$	89%	$\delta b$	64%	$\delta b$	64%	$\delta b$	55%	$\delta b$	>199%	$\delta b$	85%	$\delta b$	102%	$\delta b$	22%

and

Table 14. Here the test results between the selected material properties and selected observed fragmentation characteristics of the investigated CFs are presented similarly to Table 13. The first two columns give the results for the standard errors of the WHOFOs and HARFOs counts per volume, while the 3rd and 4th give the results for datasets where the relative errors of the counts of the mPitch 11 and 14 materials were set to 100% to reduce their χ²-fitting weight and where removed from the PC-test, see text. A small p_PC-value in the first row indicates that linear independence is unlikely. The sign indicates the slope of the correlation. A high χ²-probability of the linear fit results when it stays within the estimated experimental errors. A small relative error δb indicates that the slope of the linear fit is reliable. The color coding starts to change from green to cyan to blue for p_PC-values > 0.05 and from green to orange to red for P_ndf (χ²) < 5% or δb > 100% with RGB color mixing.

Property Group			WHOFOs per Milled CF Volume		HARFOs per Milled CF Volume		*WHOFOs11,14 per Milled CF Volume		*HARFOs11,14 per Milled CF Volume		Mean Length of WHOFOs		Mean Length of HARFOs		Mean Aspect Ratio of WHOFOs		Mean Aspect Ratio of HARFOs		Mean Diameter of WHOFOs		Mean Diameter of HARFOs		WHOFOs per HARFOs
P1	Micro- porosity $P_{\mu }$	$p_{\mathrm{P}\mathrm{C}}$	−0.011	$p_{\mathrm{P}\mathrm{C}}$	−0.028	$p_{\mathrm{P}\mathrm{C}}$	−0.003	$p_{\mathrm{P}\mathrm{C}}$	−0.088	$p_{\mathrm{P}\mathrm{C}}$	−0.711	$p_{\mathrm{P}\mathrm{C}}$	+0.066	$p_{\mathrm{P}\mathrm{C}}$	−0.010	$p_{\mathrm{P}\mathrm{C}}$	−0.004	$p_{\mathrm{P}\mathrm{C}}$	+0.016	$p_{\mathrm{P}\mathrm{C}}$	+0.021	$p_{\mathrm{P}\mathrm{C}}$	−0.037
		$P_{{\chi }^2}$	80%	$P_{{\chi }^2}$	66%	$P_{{\chi }^2}$	97%	$P_{{\chi }^2}$	84%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	81%
		$\delta b$	44%	$\delta b$	47%	$\delta b$	53%	$\delta b$	56%	$\delta b$	>199%	$\delta b$	135%	$\delta b$	189%	$\delta b$	158%	$\delta b$	125%	$\delta b$	104%	$\delta b$	39%
	Specific Density $\varrho$	$p_{\mathrm{P}\mathrm{C}}$	+0.018	$p_{\mathrm{P}\mathrm{C}}$	+0.043	$p_{\mathrm{P}\mathrm{C}}$	+0.004	$p_{\mathrm{P}\mathrm{C}}$	+0.106	$p_{\mathrm{P}\mathrm{C}}$	+0.724	$p_{\mathrm{P}\mathrm{C}}$	−0.073	$p_{\mathrm{P}\mathrm{C}}$	+0.010	$p_{\mathrm{P}\mathrm{C}}$	+0.004	$p_{\mathrm{P}\mathrm{C}}$	−0.014	$p_{\mathrm{P}\mathrm{C}}$	−0.025	$p_{\mathrm{P}\mathrm{C}}$	+0.029
		$P_{{\chi }^2}$	59%	$P_{{\chi }^2}$	42%	$P_{{\chi }^2}$	94%	$P_{{\chi }^2}$	74%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	77%
		$\delta b$	41%	$\delta b$	44%	$\delta b$	47%	$\delta b$	48%	$\delta b$	>199%	$\delta b$	142%	$\delta b$	>199%	$\delta b$	163%	$\delta b$	124%	$\delta b$	108%	$\delta b$	35%
P2	Partial Orientation $O_{\mathrm{P}}$	$p_{\mathrm{P}\mathrm{C}}$	+0.144	$p_{\mathrm{P}\mathrm{C}}$	+0.185	$p_{\mathrm{P}\mathrm{C}}$	+0.146	$p_{\mathrm{P}\mathrm{C}}$	+0.191	$p_{\mathrm{P}\mathrm{C}}$	−0.368	$p_{\mathrm{P}\mathrm{C}}$	−0.060	$p_{\mathrm{P}\mathrm{C}}$	+0.194	$p_{\mathrm{P}\mathrm{C}}$	+0.093	$p_{\mathrm{P}\mathrm{C}}$	−0.003	$p_{\mathrm{P}\mathrm{C}}$	−0.016	$p_{\mathrm{P}\mathrm{C}}$	+0.099
		$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	3%	$P_{{\chi }^2}$	5%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	3%
		$\delta b$	32%	$\delta b$	28%	$\delta b$	36%	$\delta b$	31%	$\delta b$	>199%	$\delta b$	135%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	113%	$\delta b$	111%	$\delta b$	23%
P3	Interlayer Spacing $d_{002}$	$p_{\mathrm{P}\mathrm{C}}$	−0.253	$p_{\mathrm{P}\mathrm{C}}$	−0.374	$p_{\mathrm{P}\mathrm{C}}$	−0.055	$p_{\mathrm{P}\mathrm{C}}$	−0.300	$p_{\mathrm{P}\mathrm{C}}$	+0.969	$p_{\mathrm{P}\mathrm{C}}$	+0.196	$p_{\mathrm{P}\mathrm{C}}$	−0.067	$p_{\mathrm{P}\mathrm{C}}$	−0.026	$p_{\mathrm{P}\mathrm{C}}$	+0.019	$p_{\mathrm{P}\mathrm{C}}$	+0.112	$p_{\mathrm{P}\mathrm{C}}$	−0.020
		$P_{{\chi }^2}$	2%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	29%	$P_{{\chi }^2}$	22%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	58%
		$\delta b$	53%	$\delta b$	67%	$\delta b$	41%	$\delta b$	37%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	125%	$\delta b$	188%	$\delta b$	30%
	Tensile Modulus $E_{\mathrm{L}}$	$p_{\mathrm{P}\mathrm{C}}$	+0.172	$p_{\mathrm{P}\mathrm{C}}$	+0.276	$p_{\mathrm{P}\mathrm{C}}$	+0.010	$p_{\mathrm{P}\mathrm{C}}$	+0.139	$p_{\mathrm{P}\mathrm{C}}$	+0.704	$p_{\mathrm{P}\mathrm{C}}$	−0.141	$p_{\mathrm{P}\mathrm{C}}$	+0.010	$p_{\mathrm{P}\mathrm{C}}$	+0.003	$p_{\mathrm{P}\mathrm{C}}$	−0.013	$p_{\mathrm{P}\mathrm{C}}$	−0.059	$p_{\mathrm{P}\mathrm{C}}$	+0.012
		$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	13%	$P_{{\chi }^2}$	19%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	35%
		$\delta b$	27%	$\delta b$	25%	$\delta b$	31%	$\delta b$	28%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	124%	$\delta b$	147%	$\delta b$	21%
	Crystallite Size ${\mathrm{l}\mathrm{o}\mathrm{g}(L}_{a\perp })$	$p_{\mathrm{P}\mathrm{C}}$	+0.104	$p_{\mathrm{P}\mathrm{C}}$	+0.188	$p_{\mathrm{P}\mathrm{C}}$	+0.018	$p_{\mathrm{P}\mathrm{C}}$	+0.244	$p_{\mathrm{P}\mathrm{C}}$	+0.631	$p_{\mathrm{P}\mathrm{C}}$	−0.109	$p_{\mathrm{P}\mathrm{C}}$	+0.013	$p_{\mathrm{P}\mathrm{C}}$	+0.007	$p_{\mathrm{P}\mathrm{C}}$	−0.018	$p_{\mathrm{P}\mathrm{C}}$	−0.062	$p_{\mathrm{P}\mathrm{C}}$	+0.006
		$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	10%	$P_{{\chi }^2}$	9%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	28%
		$\delta b$	31%	$\delta b$	28%	$\delta b$	35%	$\delta b$	31%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	126%	$\delta b$	137%	$\delta b$	20%
	Crystallite Size ${\mathrm{l}\mathrm{o}g(L}_{a\left|\right|})$	$p_{\mathrm{P}\mathrm{C}}$	+0.021	$p_{\mathrm{P}\mathrm{C}}$	+0.047	$p_{\mathrm{P}\mathrm{C}}$	+0.031	$p_{\mathrm{P}\mathrm{C}}$	+0.287	$p_{\mathrm{P}\mathrm{C}}$	+0.819	$p_{\mathrm{P}\mathrm{C}}$	−0.086	$p_{\mathrm{P}\mathrm{C}}$	+0.023	$p_{\mathrm{P}\mathrm{C}}$	+0.015	$p_{\mathrm{P}\mathrm{C}}$	−0.019	$p_{\mathrm{P}\mathrm{C}}$	−0.056	$p_{\mathrm{P}\mathrm{C}}$	+0.035
		$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	5%	$P_{{\chi }^2}$	11%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	3%
		$\delta b$	31%	$\delta b$	26%	$\delta b$	36%	$\delta b$	30%	$\delta b$	>199%	$\delta b$	159%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	126%	$\delta b$	125%	$\delta b$	22%
	Thermal Conductivity ${\mathrm{l}\mathrm{o}\mathrm{g}(q}_{\mathrm{T}})$	$p_{\mathrm{P}\mathrm{C}}$	+0.180	$p_{\mathrm{P}\mathrm{C}}$	+0.283	$p_{\mathrm{P}\mathrm{C}}$	+0.017	$p_{\mathrm{P}\mathrm{C}}$	+0.162	$p_{\mathrm{P}\mathrm{C}}$	+0.898	$p_{\mathrm{P}\mathrm{C}}$	−0.163	$p_{\mathrm{P}\mathrm{C}}$	+0.022	$p_{\mathrm{P}\mathrm{C}}$	+0.005	$p_{\mathrm{P}\mathrm{C}}$	−0.008	$p_{\mathrm{P}\mathrm{C}}$	−0.059	$p_{\mathrm{P}\mathrm{C}}$	+0.013
		$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	6%	$P_{{\chi }^2}$	11%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	24%
		$\delta b$	35%	$\delta b$	30%	$\delta b$	38%	$\delta b$	33%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	118%	$\delta b$	152%	$\delta b$	19%
	Raman Area Ratio $\mathrm{l}\mathrm{o}\mathrm{g}(A_{\mathrm{G}}/A_{\mathrm{D}})$	$p_{\mathrm{P}\mathrm{C}}$	+0.192	$p_{\mathrm{P}\mathrm{C}}$	+0.305	$p_{\mathrm{P}\mathrm{C}}$	+0.027	$p_{\mathrm{P}\mathrm{C}}$	+0.243	$p_{\mathrm{P}\mathrm{C}}$	+0.415	$p_{\mathrm{P}\mathrm{C}}$	−0.312	$p_{\mathrm{P}\mathrm{C}}$	+0.010	$p_{\mathrm{P}\mathrm{C}}$	+0.005	$p_{\mathrm{P}\mathrm{C}}$	−0.074	$p_{\mathrm{P}\mathrm{C}}$	−0.202	$p_{\mathrm{P}\mathrm{C}}$	+0.038
		$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	3%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	10%
		$\delta b$	35%	$\delta b$	28%	$\delta b$	41%	$\delta b$	32%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	149%	$\delta b$	197%	$\delta b$	19%
	Elongation at Break ${\epsilon }_{\mathrm{B}}$	$p_{\mathrm{P}\mathrm{C}}$	−0.058	$p_{\mathrm{P}\mathrm{C}}$	−0.099	$p_{\mathrm{P}\mathrm{C}}$	−0.110	$p_{\mathrm{P}\mathrm{C}}$	−0.406	$p_{\mathrm{P}\mathrm{C}}$	+0.992	$p_{\mathrm{P}\mathrm{C}}$	+0.084	$p_{\mathrm{P}\mathrm{C}}$	−0.053	$p_{\mathrm{P}\mathrm{C}}$	−0.052	$p_{\mathrm{P}\mathrm{C}}$	+0.013	$p_{\mathrm{P}\mathrm{C}}$	+0.070	$p_{\mathrm{P}\mathrm{C}}$	−0.055
		$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	2%	$P_{{\chi }^2}$	4%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	3%
		$\delta b$	29%	$\delta b$	30%	$\delta b$	40%	$\delta b$	34%	$\delta b$	>199%	$\delta b$	162%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	121%	$\delta b$	134%	$\delta b$	23%
P4	Tensile Strength ${\sigma }_{\mathrm{T}}$	$p_{\mathrm{P}\mathrm{C}}$	−0.564	$p_{\mathrm{P}\mathrm{C}}$	−0.596	$p_{\mathrm{P}\mathrm{C}}$	+0.760	$p_{\mathrm{P}\mathrm{C}}$	+0.380	$p_{\mathrm{P}\mathrm{C}}$	−0.128	$p_{\mathrm{P}\mathrm{C}}$	−0.680	$p_{\mathrm{P}\mathrm{C}}$	−0.497	$p_{\mathrm{P}\mathrm{C}}$	−0.877	$p_{\mathrm{P}\mathrm{C}}$	−0.648	$p_{\mathrm{P}\mathrm{C}}$	−0.447	$p_{\mathrm{P}\mathrm{C}}$	+0.935
		$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	2%	$P_{{\chi }^2}$	2%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	97%	$P_{{\chi }^2}$	0%
		$\delta b$	38%	$\delta b$	33%	$\delta b$	38%	$\delta b$	34%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	35%
P5	Initial Diameter $d_{\mathrm{i}}$	$p_{\mathrm{P}\mathrm{C}}$	+0.233	$p_{\mathrm{P}\mathrm{C}}$	+0.316	$p_{\mathrm{P}\mathrm{C}}$	+0.236	$p_{\mathrm{P}\mathrm{C}}$	+0.673	$p_{\mathrm{P}\mathrm{C}}$	+0.018	$p_{\mathrm{P}\mathrm{C}}$	−0.867	$p_{\mathrm{P}\mathrm{C}}$	+0.012	$p_{\mathrm{P}\mathrm{C}}$	+0.062	$p_{\mathrm{P}\mathrm{C}}$	−0.580	$p_{\mathrm{P}\mathrm{C}}$	−0.743	$p_{\mathrm{P}\mathrm{C}}$	+0.264
		$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	0%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	1%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	100%	$P_{{\chi }^2}$	99%	$P_{{\chi }^2}$	98%	$P_{{\chi }^2}$	10%
		$\delta b$	52%	$\delta b$	45%	$\delta b$	52%	$\delta b$	45%	$\delta b$	159%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	>199%	$\delta b$	176%	$\delta b$	27%

*WHOFO^11,14 and *HARFO^11,14 denote datasets where the relative errors of the counts of the mPitch 11 and 14 materials were set to 100% to reduce their χ²-fitting weight and where removed from the PC-test, see text.

. Alternatively the average χ²-contribution per degree-of-freedom χ²/ndf can be examined. The corresponding χ²-probability P_ndf(χ²) is tabulated in Table 12 for ndf = 7. The average χ²-contribution per degree-of-freedom for a significance level of P_ndf(χ²) = α = 5% is approximately χ²/ndf = 2.

Table 11, Table 13 and Table 14 report Pearson’s $p_{\mathrm{P}\mathrm{C}}$-values resulting from testing the null hypothesis for linear independence together with a superscript “+/−“ indicating positive or negative correlations. For $p_{\mathrm{P}\mathrm{C}}$-values below a selected significance level α = 0.05, it is considered unlikely that the two tested datasets are linearly independent and the alternative hypothesis of a linear correlation is accepted.

Some material properties varied non-linearly over wide ranges of values. This means, the variable’s values develop non-linearly with respect to one member of a group of linearly correlated variables. To test for such logarithmic dependence, logarithmic rescaling operations were applied prior to linearity testing. In this way, for some properties, also the statistical significance of normality, the p_KS-value, was also increased together with a decrease in the p_PC-value, i.e., the significance of linear independence to a chosen reference property, here density ϱ, see Table 10.

Provided valid error estimates are used, the χ²-test is superior to the purely statistical PC-test because it incorporates knowledge of the physical data quality. However, only the errors must be small relative to the data range to provide leverage and impose sufficiently rigid constraints on the fit. Otherwise the errors on the fitted parameters $a$ and $b$ will be relatively large. The relative error on the slope δb provides a way of assessing whether any useful information has been gained from the error-weighted fit. If δb is found to be greater than approximately 100%, the PC-test should be used as a fall-back criterion for linear dependence.

In the Table 12, Table 13 and Table 14, a cell color coding scheme is used to visualize the results of both test approaches. In the RGB color space, the two color axes blue (for increasing p_PC-value) and red (for decreasing P_ndf (χ²) or increasing δb-error) were used to indicate the deviation from linear dependence, shown in green. In the following, only data pairs with green and cyan cells are considered to be linearly correlated, e.g., Figure 6. All others require detailed consideration.

• Green cells: Data with high χ²-probability P_ndf(χ²), small δb-error and small p_PC-value
• Cyan to blue cells: Data with P_ndf(χ²) ≥ 5%, δb-error < 100% but a p_PC-value > 0.05
• Yellow to orange cells: Data with reduced P_ndf(χ²) or large δb > 100% but small p_PC-value < 0.05
• Red to purple cells: Data with low Pndf(χ²) < 5% or large δb > 100% and high p_PC-value > 0.05.

For cyan cells with moderate to high χ²-probability and small δb-error $<100\%$ but p_PC-values well above 0.05, χ²-testing was generally more informative than PC-testing.

Orange cells with small p_PC-value but low χ²-probability or large δb-error $\ge 200\%$ indicate that the data were either incompatible with the error model or the errors were too large to provide usable information on the slope, respectively. The small p_PC-value of the purely statistical PC-test may therefore help to detect a linear dependence. In most cases, however, the PC-test based on only 9 data pairs turned out to be statistically too weak to distinguish balanced data scatter from non-correlation, cf. Figure 7.

For red cells with p_PC-values > 0.05, high χ²-probability but large δb-error ≥ 200%, the purely statistical PC-test may be more informative and help to identify non-linear trends in the data, cf. Figure 8. Consequently, purple cells with their high p_PC-values were reliably identified as non-correlated.

Due to the limitations of the statistical methods for ensembles of nine data points, this very detailed approach to consider all available experimental information, including error estimates, seemed necessary to substantiate the subsequent discussion of correlations between material parameters and experimentally observed fragment morphologies.

4.3.2. Correlations among Material Properties

The material properties of the investigated CF materials were subjected to PC- and χ²-tests in order to identify possible mutual linear dependencies. For the subsequent discussion, the following groups of material properties were defined according to the structure of the results in Table 14

(P1)

Microporosity P_µ and specific density ϱ

(P2)

Partial orientation O_P

(P3)

Interlayer spacing d₀₀₂, thermal volume conductivity q_T, tensile

• Modulus E_M, crystallite domain size parallel $L_{\mathrm{a}\Vert }$ and perpendicular to fiber axis $L_{\mathrm{a}}$, Raman area ratio $A_{\mathrm{G}}/A_{\mathrm{D}}$ and elongation at break ${\epsilon }_{\mathrm{B}}$. The linear correlation between the characteristic domain size $L_{\mathrm{c}}$ and $L_{\mathrm{a}\Vert }$ was practically perfect, so $L_{\mathrm{c}}$ was omitted for the subsequent discussion.

(P4)

Tensile Strength σ_T

(P5)

Initial CF diameter d_i.

The results in Table 13 lead to the following interpretation

• Since tensile strength ${\sigma }_{\mathrm{T}}$(P4) results from plastic deformation behavior in the non-linear part of the stress-strain relationship, no linear correlation with the other properties was found here, except perhaps with initial diameter $d_{\mathrm{i}}$ (P5), although this relationship was supported only by PC-statistics only by the ${\chi }^2$-test, see Figure 9
• The initial fiber diameter $d_{\mathrm{i}}$ (P5) shows an apparent correlation with microporosity $P_{\mu }$ and density $\varrho$ only for Group P1, as the higher graphitized mPitchCFs were produced with generally larger diameters
• The properties microporosity $P_{\mu }$ and density $\varrho$ of Group P1 are mutually correlated as $P_{\mu }$ is proportional to the product of the interlayer distance $d_{002}$ and $\varrho$∙ These Group P1 properties $P_{\mu }$ and $\varrho$ are also well correlated with the properties of Group P2 and P3
• Within property Group P3 only the interlayer distance $d_{002}$ is correlated with all others
• A too large Raman area ratio $A_{\mathrm{G}}/A_{\mathrm{D}}$ of iPitchCF 12 is responsible for the non-correlation in Group P3, although the other materials show linear trends, see Figure 10.
• The logarithm of the domain size $L_{\mathrm{a}\Vert }$ and $L_{\mathrm{a}}$ seems to correlate well with the elongation at break ${\epsilon }_{\mathrm{B}}$, see Figure 11.

4.3.3. Correlations between Observed Fragmentation Characteristics and Material Properties

It would be desirable to be able to predict the propensities of fiber fragmentation from material properties. The main objective of the present work was therefore to investigate relationships between material properties and the observed fragmentation characteristics. The grouping of material properties introduced earlier was intended to provide a structural order of the results in Table 14.

Notable observations on correlations between observables and material properties in Table 14 include

• Diameter of WHOFOs and HARFOs: According to PC- and χ²-tests, the mean diameters of the WHOFOs and HARFOs were linearly correlated with the property Groups P1 (high $P_{\mu }$ and low $\varrho$), P2 (low $O_{\mathrm{P}}$) and, partially, P3 (large $d_{002}$, low $q_{\mathrm{T}}$, small $L_{a\perp }$, $L_{a\Vert }$ and $E_L$, low $A_{\mathrm{G}}/A_{\mathrm{D}}$ and high ${\epsilon }_{\mathrm{B}}$). However, due to the large statistical error in the diameters of the WHOFO and HARFO ensembles of about 33%, a large relative error $\delta b$ resulted, limiting the information on the slope $b$ of the linear function obtained from the fit.
• Length of WHOFOs and HARFOs: The statistical errors on the lengths of the WHOFO and HARFO ensembles were also large (about 30%), especially for panCF 8, and resulted in a relative error $\delta b$ in the fitted slope of more than 200%. In addition, PC-testing showed high significance for linear independence (red to purple cells). Therefore, there was no convincing evidence of a correlation between the mean WHOFO lengths and the tested property Groups P1–P5. Also the slightly smaller relative error $\delta b$ for the mean HARFO lengths and P1–P2 did not result in a convincing relationship.
• Aspect ratio of WHOFOs and HARFOs: As the relative error in aspect ratio is the sum of the relative errors in length and diameter, the power of the ${\chi }^2$-test is also weak for these observables. All properties are compatible with error-weighted linear fits to the aspect ratio, but the large errors do not significantly constrain the slope $b$. However, the trends that the aspect ratio of fragments increases with the material quality are also supported by the PC-tests, except for P2 and P4.
• Ratio of WHOFOs to HARFOs: The formation of WHOFOs relative to HARFOs was favored by the two characteristics of Group P1 (low $P_{\mu }$ and high $\varrho$) and partially by P3 (small $d_{002}$, high $q_{\mathrm{T}}$, large $L_{a\perp }$, $E_L$ and high $A_{\mathrm{G}}/A_{\mathrm{D}}$). As a general trend, the ratio of WHOFO to HARFO fragments increased with material quality. The apparent correlation with the initial diameter $d_{\mathrm{i}}$, on closer inspection, actually looks like random scatter, biased by the larger synthesis diameters of mPitchCFs 10 and 11.
• Number of WHOFOs formed: Most important for the subsequent discussion of risk assessment is the number of WHO fibers formed per volume of CF milled. The WHOFO count appears to be linearly dependent on the two properties low $P_{\mu }$ and high $\varrho$ of Group P1. Figure 12 shows that, due to the clustering of the PAN and iPitch CF data points, the leverage of the mPitchCF 11 and 14 data points determines the outcome of the fit. However, plotting the WHOFO counts against the important material property longitudinal tensile modulus $E_{\mathrm{L}}$ in Figure 13 shows the following trend, which is also found for the other properties of Group P3: All data points of the PAN and iPitch materials are aligned in the direction of the mPitchCF 10 data point. This could be interpreted as a linear relationship between the material properties of Group P3 and the propensities to form WHO fiber fragments. However, this linearity does not include the mPitchCFs 11 and 14 materials! These released drastically higher numbers of WHOFOs than their material parameters would imply for a linear relationship. If we consider the WHOFO concentrations observed for iPitchCF, panCFs and mPitchCF 10 to be reliable and the linear correlation with the P3 properties to be significant, we can determine the either unweighted or weighted linear correlation by fitting with the WHOFO data of mPitchCFs 11 and 14, which were either omitted or reduced in weight, respectively, cf. Figure 13 and Figure 14. The fit weight reduction was technically achieved by setting the relative errors in the WHOFO counts to 100%. The revised linear model marks mPitchCFs 11 and 14 as materials with excessive WHOFO formation.

This alternative strategy of excluding mPitchCFs 11 and 14 from fitting, results in an additional pair of columns for the WHOFOs and HARFOs per milled CF volume in Table 14, denoted by superscripts 11 and 14. For this alternative data weighting, the WHOFO and HARFO counts correlated well with the material properties of Group P1 and P3 except for log(A_G/A_D) and ε_B.

These results could be interpreted in the following two ways

• The WHOFO and HARFO counts of the most graphitic mPitch CF material 10 were systematically underestimated due to non-brittle transformation of fragments to unquantifiable graphitic smear by ball impact.
• Not yet understood and not-quantitatively described microstructural properties of the highly lamellar mPitch CF materials 11 and 14 determined their excessive disintegration characteristics into fibrous fragments, cf. Figure 2.

As a general trend, the aspect ratios and also the ratios of WHOFO to HARFO fragments increased with the material quality, i.e., the degree of structural order (lower $P_{\mu }$, higher $\varrho$, higher $O_{\mathrm{P}}$, smaller $d_{002}$, larger $L_{a\perp }$), which is accompanied by higher $q_{\mathrm{T}}$ and $E_{\mathrm{L}}$.

However, all these correlations or non-correlations do not explain why panCF 1 behaved very differently when compared to the other panCFs. As details of the manufacturing processes are not known, some factors may not be tangible. Differences in the precursor or its pre-treatment, phase transitions of the liquid crystal or finishing steps may play a role.

4.3.4. Correlations among Observed Fragmentation Characteristics

PC- and χ²-tests were also performed on the observed fragmentation characteristics of the studied CF materials after ball milling. The aim was to identify possible mutual linear dependencies. However, Table 11 shows a rather complex correlation pattern between the observables.

Notable observations include

• The concentrations of formed WHO and HAR fiber objects per milled CF volume were correlated.
• The observation that the ratio of formed WHOFOs to HARFOs increased with mean aspect ratio and decreased with mean WHOFO diameter is plausible, but the estimated errors of the WHOFO and HARFO length, diameter and aspect ratio are rather large, so the power of the χ²-test is limited here, cf. Figure 15.
• For the same milled CF volume, materials that produced WHOFO and HARFO fragments with small mean diameters, cf. Figure 16, and HARFOs with small mean lengths, cf. Figure 17, tended to produce more WHOFO and HARFO objects. However, this trend only holds when the mPitchCFs 11 and 14 are included in the correlation analysis.

The observable presented in

Table 15. Mean and maximum observed lengths of HARFOs (top) and WHOFOs (bottom) compared to the initial CF diameter $d_i$.

HARFOs
Measurand	12 iPitch	1 PAN	8 PAN	5 PAN	4 PAN	15 PAN	14 mPitch	11 mPitch	10 mPitch
Initial Diameter $d_{\mathrm{i}}$ [µm]	10.0	7.0	7.0	5.0	4.9	4.4	7.0	11.0	11.0
Mean Length $<L_{\mathrm{H}\mathrm{A}\mathrm{R}\mathrm{F}\mathrm{O}}>$ [µm]	17.7	7.4	19.3	13.5	9.9	11.6	6.4	6.4	10.5
Ratio $<L_{\mathrm{H}\mathrm{A}\mathrm{R}\mathrm{F}\mathrm{O}}>/d_{\mathrm{i}}$ [1]	1.8	1.1	2.8	2.7	2.0	2.6	0.9	0.6	1.0
Maximum Length ${\widehat{L}}_{\mathrm{H}\mathrm{A}\mathrm{R}\mathrm{F}\mathrm{O}}$ [µm]	42.5	45.6	132.9	92.2	22.4	28.8	43.0	46.4	59.2
Ratio ${\widehat{L}}_{\mathrm{H}\mathrm{A}\mathrm{R}\mathrm{F}\mathrm{O}}/d_{\mathrm{i}}$ [1]	4.3	6.5	19.0	18.4	4.6	6.5	6.1	4.2	5.4
WHOFOs
Measurand	12 iPitch	1 PAN	8 PAN	5 PAN	4 PAN	15 PAN	14 mPitch	11 mPitch	10 mPitch
Initial Diameter $d_{\mathrm{i}}$ [µm]	10.0	7.0	7.0	5.0	4.9	4.4	7.0	11.0	11.0
Mean Length $<L_{\mathrm{W}\mathrm{H}\mathrm{O}\mathrm{F}\mathrm{O}}>$ [µm]	10.4	8.8	7.9	7.5	7.6	7.1	8.0	8.0	10.9
Ratio $<L_{\mathrm{W}\mathrm{H}\mathrm{O}\mathrm{F}\mathrm{O}}>/d_{\mathrm{i}}$ [1]	1.0	1.3	1.1	1.5	1.6	1.6	1.1	0.7	1.0
Maximum Length ${\widehat{L}}_{\mathrm{W}\mathrm{H}\mathrm{O}\mathrm{F}\mathrm{O}}$ [µm]	16.8	13.8	13.4	9.2	12.2	11.8	14.9	13.6	42.4
Ratio ${\widehat{L}}_{\mathrm{W}\mathrm{H}\mathrm{O}\mathrm{F}\mathrm{O}}/d_{\mathrm{i}}$ [1]	1.7	2.0	1.9	1.8	2.5	2.7	2.1	1.2	3.9

require the morphological evaluation of all identified fiber-shaped fragments. The observed linear dependence between the mean HARFO diameters and lengths and the WHOFOs per milled volume suggests that mean HARFO diameter and length may serve as a proxy. However, it is not a means of reducing the high analytical workload required for the morphological characterization of the fragment ensemble.

4.4. Material- and Microstructure-Related Fragmentation Differences

The present study investigated the relative differences in the formation of respirable fiber fragments between PAN- and mPitch-based CFs. Such differences have been reported previously. However, the differences between PAN- and mPitch CFs in the propensity to form WHO-fibers observed in this work, in terms of the volume of fibers ground, were smaller than expected, in most cases less than an order of magnitude.

It should be noted that panCFs can also form WHO-fiber fragments in situations of mechanical overload. Such fragments have to be considered as potentially carcinogenic and urgently require appropriate toxicological testing. Earlier statements [38,64,65,66] that carbon fibers per se do not break along their fiber axis, do not form respirable fiber dusts and are therefore intrinsically safe have been refuted by this and our previous study [7]. Therefore, it does not seem justified to neglect the potential release of toxicologically relevant fragments from CF-containing materials.

The observed fragmentation differences may be due partially to the chemical structure of the high-molecular weight precursor molecules and partly to the synthesis processes. Their correlation with standard material properties alone, such as tensile modulus, specific density or conductivity, was not convincing. In particular, a better understanding of the differences between panCF 1 and panCF 8 or panCF 15 and mPitchCF 14 is desirable.

4.4.1. Material Property Effects

It is noteworthy that CF material pairs with very similar material properties according to Table 2, namely panCFs 1 and 8 as well as panCF 15 and mPitchCF 14, showed very different fragmentation behavior during ball milling. For panCF 1 and 8, the reason for this difference is unclear as the result of the crystallographic and Raman analyzes results were also similar. For panCF 15 and mPitchCF 14, the much smaller diameter of the UHM panCF (4.4 µm versus 11 µm) may be responsible for the reduced propensity to form fiber fragments, although also XRD and Raman also indicated additional microstructural differences.

The relationships between material properties and the underlying crystalline structure are complex and not fully understood. For example, the mesophase pitch fiber 10 has by far the highest degree of graphitization. Consistent with its large crystalline domain size, it formed the highest percentage of HARFO and WHOFO fragments relative to all fragments formed. However, of the three mPitchCFs investigated, CF 10 formed the smallest absolute number of HAR- and WHO-fiber fragments, cf. Table 7. There are at least two possible explanations for this observation: Firstly, its high degree of graphitization, which may result in a plastically deformable material capable of forming recompressed multi-fragment agglomerates under ball mill impact. Alternatively, due to its significantly higher tensile modulus than the other mPitchCFs, mechanical failure of the CF material may consume more impact energy and thus form fewer fragments under identical ball mill conditions.

4.4.2. Microstructural Effects

Unlike polyacrylonitrile, mesophase pitches, the precursors of mPitchCFs, contain polyaromatic molecular domains that tend to align by $\pi$-stacking and form liquid crystal phases such as nematic, smectic or discotic. Such molecular pre-orientation, enhanced by stretching of the spun filaments promotes the formation of a polycrystalline CF microstructure during the carbonization and graphitization stages of fiber synthesis. The higher the graphitization temperature and duration, the larger the crystalline domains of the layered structure can grow. Large crystalline domains that are oriented in the direction of the fiber axis by yarn stretching are believed to be responsible for the increased propensity of mPitch CFs to disintegrate into fiber-shaped fragments.

The mPitchCFs studied here were characterized by their large crystalline domain sizes parallel and perpendicular to the fiber axis together with low microporosity. They released significantly more, but not orders of magnitude more, HAR- and WHO-fragments per milled fiber volume than the studied PAN-based CFs with their smaller domain size and higher microporosity.

Among the three mPitchCF studied, differences in crystalline microstructure seem to influence the spallation characteristics as both mPitchCF 10 and 14 show a less radially-ordered lamellar structure of their cross section in Figure 2 than mPitchCF 11, which produced by far the largest number of HARFOs and WHOFOs per milled CF length.

4.4.3. Direction of Filament Fragmentation

For all observed high-aspect ratio fragments, the maximum allowable fracture angles $\phi$, as defined in Figure 18, were calculated and averaged. Plotting the data against a length-related metric in Figure 19 highlights the effects of the initial CF diameter. Propagation of statistically independent offset $a$ and slope $b$ errors gives the shown grey error band of the linear function in the form of $y\pm \mathsf{\Delta }y=\left(a+b·x\right)\pm \sqrt{\mathsf{\Delta }{a}^2+(\mathsf{\Delta }{b·x)}^2}$. The plot suggests that the LD-HARFO group of materials tended to break more perpendicular to the fiber axis, i.e., at larger angles. The LDH materials mPitchCF 10, 11, 14 and panCF 1 not only consisted of initially thicker CFs but also formed shorter HARFOs on average, cf. Figure 4 and Table 15. This upper limit of the fracture angle derived from fragment length and initial CF diameter therefore does not support the hypothesis of a fragmentation along the CF axis for the LDH group of materials.

Despite a higher microstructural orientation of mPitchCFs than panCFs, the fragmentation direction that can be constrained by the ratio of initial diameter to fragment length, as defined in Figure 18, does not support the hypothesis that mPitchCF fragment formation preferentially occurs in the direction of the CF axis.

However, SEM micrographs consistently showed fragment morphologies of mPitchCFs that were characteristic of fragmentation along the major axis, cf. Figure 20. The present work, similar to Ref. [7], supports the assumption that mPitchCFs form fragments preferentially in the direction of the CF axis. However, such a disintegration pattern did not systematically result in longer fragments, as the fragments were also thinner, cf. Figure 4.

Although the panCF and iPitchCF materials investigated had a lower crystalline orientation than the mPitchCFs, the reverse assumption that panCFs have a lower tendency to fracture along the fiber axis could not be substantiated here: For all panCFs, e.g., the ratio of the longest observed WHO-fragment to the initial diameter remained above 1.8, cf. Table 15, and smaller breaking angle limits were estimated for HARFOs in Figure 19.

Unlike mesophase pitch and similar to PAN, isotropic pitch does not exhibit liquid crystal properties. Less crystalline, more granular microstructures were also observed for the panCFs and the iPitchCF studied in Figure 2. This helps to understand the similarity of iPitchCF 12 to the studied panCFs with in terms of material properties and fracture characteristics and effectively increased the proportion of fragments that maintained the diameter of the initial fiber in at least one direction during ball milling, cf. Figure 4.

4.5. Carbon Fiber Diameter Paradox

Since only fibers thinner than about $3 \mathrm{\mu }\mathrm{m}$ are considered respirable, commercial CF materials are designed to exceed this toxicologically critical respirable diameter. It may therefore be surprising that for the CF materials investigated here, those with a smaller initial diameter actually showed a reduced hazard potential due to their fragment morphology: CF materials thinner than or equal $5\mathrm{\mu }\mathrm{m}$ showed a higher tendency to form large diameter HARFOs (Figure 21) and shorter WHOFOs (Figure 22). They also produced fragments with larger wedge opening angles (Figure 23). A smaller initial CF diameter may therefore help to reduce the propensity to form fragments of WHO-fiber morphology but is prone to cause problems for CFRP recycling, as even minor diameter thinning during pyrolysis processes brings it closer to the respirable threshold. Such CF diameter thinning can occur during a final purification step of pyrolysis in a hot oxygen-containing atmosphere used to remove polyaromatic hydrocarbon residues and soot.

4.6. Identification of Critical CF Materials

Although no strong linear correlation could be identified here that would be suitable for predicting the fragmentation behavior of carbon fibers and ranking their risk potential, it is still possible to divide the studied CF types into two categories: Carbon fibers with a specific density above 1.95 g/cm³ with a high propensity to form WHOFOs during ball milling, and those below this threshold, see Figure 24. This threshold density of $1.95 \mathrm{g}/{\mathrm{c}\mathrm{m}}^3$ could be used as an easily applicable criterion to indicate a potentially excessive propensity to form WHOFOs during mechanical disintegration.

The mean diameter of the HAR-fragments formed during mechanical disintegration is also an important characteristic as it can directly influence the number of fiber fragments formed: The thinner the mean HARFO diameter, the more HARFOs can be produced from the same volume of disintegrated material.

For the entire HARFO ensemble, the differences in the elastic modulus generally had no significant effect on their aspect ratio, see Figure 25, except for mPitchCF 10 with its extremely high tensile modulus. Therefore, thinner HARFO fragments tended to break more easily and were shorter on average.

However, as this average fragment length was still above the 5 µm length threshold for WHO-fibers, the tendency of LDH materials to form thinner HARFOs (by definition), resulted in a higher percentage of WHOFOs than for HDH materials. For these HARFOs thinner than $3 \mathrm{\mu }\mathrm{m}$, the higher tensile modulus values of the mPitchCFs seemed to have an effect and influenced the aspect ratio, see Figure 26. The total number of WHOFOs formed is of course the product of the fraction of HARFOs with less 3 µm diameter and the number of HARFOs formed.

Figure 4 and Figure 5 show that our LD-HARFOs were on average half as thick and half as long as the HD-HARFOs. This is due to HARFO fragments maintaining the original fiber diameter. Assuming that only HARFOs are formed, in a first approximation, 2² × 2 = 8 times more LD-HARFOs than HD-HARFOs could be formed by milling the same volume of CF. Summing up the actual number of HARFOs formed per milled picoliter gave a ratio of LD-/HD-HARFOS of (79 ± 9)/(13 ± 1) = (6 ± 1). Since the HDH materials generally formed a higher proportion of LARPOs, even greater differences in HARFOs per milled CF volume between HDH and LDH materials can be understood. Consequently, the total volume formed by WHOFOs in relation to the total milled CF volume is larger for the LDH materials 1, 10, 11 and 14, see

Table 16. Volume-related results of fiber-shaped fragments after ball milling. HARFSs denote HAROFs with diameters below the initial CF diameter. The assumed of cylindrical fragments gives rise to volume overestimation when using the width of oblate objects.

Fiber ID	Mean HARFO Volume [µm3]	Mean Length of HARFOs [µm]	Mean Diameter of HARFOs [µm]	HARFOs per Milled CF Volume [1/pL]	LARPOs of Initial Diameter [%]	Total Volume of HARFOs per Milled Volume [%]	Total Volume of HARFSs per Milled Volume [%]	Total Volume of WHOFOs per Milled Volume [%]
12 iPitch	632 ± 890	17.7 ± 12.5	4.3 ± 3.0	1.3 ± 0.4	5.5 ± 1.1	82.1 ± 20.6	48.2 ± 12.3	1.3 ± 0.4
1 PAN	104 ± 341	7.4 ± 8.6	1.7 ± 1.6	6.2 ± 1.7	2.9 ± 0.8	64.4 ± 16.1	14.4 ± 3.6	3.2 ± 0.8
8 PAN	536 ± 896	19.3 ± 21.8	3.7 ± 2.7	1.7 ± 0.5	6.7 ± 1.2	89.5 ± 21.8	14.8 ± 3.6	0.8 ± 0.2
5 PAN	197 ± 341	13.5 ± 15.9	2.7 ± 1.9	4.0 ± 1.1	5.5 ± 1.0	79.0 ± 19.2	7.9 ± 1.9	2.5 ± 0.6
4 PAN	96 ± 130	9.9 ± 6.4	2.3 ± 1.6	2.5 ± 0.8	4.0 ± 0.9	24.2 ± 6.0	9.9 ± 2.5	2.1 ± 0.5
15 PAN	139 ± 138	11.6 ± 7.6	2.8 ± 1.7	3.5 ± 0.9	10.5 ± 1.5	48.6 ± 11.7	2.3 ± 0.6	1.5 ± 0.4
14 mPitch	56 ± 227	6.4 ± 5.9	1.4 ± 1.5	31.2 ± 7.7	1.0 ± 0.4	174.6 ± 41.7	55.4 ± 13.2	24.5 ± 5.8
11 mPitch	62 ± 363	6.4 ± 5.3	1.3 ± 1.4	34.8 ± 8.6	0.9 ± 0.4	216.0 ± 51.5	115.1 ± 27.4	19.3 ± 4.6
10 mPitch	89 ± 379	10.5 ± 7.4	1.8 ± 1.5	6.5 ± 1.6	0	57.5 ± 13.6	40.1 ± 9.5	10.0 ± 2.4

, Figure 26 and Figure 27. The quadratic dependence of the volume of a HARFO on its diameter implies that CF materials that tend to form thicker fragments can reduce the number of WHOFOs formed more efficiently than by fragmentation into shorter fragments, a process that only scales linearly.

The following material-specific disintegration characteristics can be derived from the data analysis above

• CF materials of higher graphitization, density, microstructural order, and mechanical and thermal performance, as characterized by the material parameter Groups P1–P4, tended to form

  ○

  WHOFOs of smaller diameter, see Figure 28

  • as well as

  ○

  higher ratios of WHOFOs to HARFOs; the highest correlation was found to the crystallite domain size perpendicular to the fiber axis, see Figure 29.

• Among these parameters (P1)–(P4), those that characterize higher microstructural order (P2), namely density $\varrho$, microporosity P_µ and crystalline order in fiber direction $L_{a\left|\right|}$, also correlated to the number of WHOFOs formed, see Figure 24, and to a decrease in the number of HARFOs thicker than the WHO-fiber diameter threshold of 3 µm, see Figure 30.
• With respect to HARFO formation, mean HARFO lengths and diameters were highly correlated: Longer fragments tended to be thicker, see Figure 31. In other words, the aspect ratio of the HARFOs did not significantly depend on tensile modulus, see Figure 32.
• Surprisingly, the lengths and aspect ratios of WHOFOs formed correlated to the initial fiber diameter d_i, see Figure 22. A possible physical origin of this correlation is unclear. It may be a side effect of the fact that the CFs of the LD-HARFO group that generally formed more WHOFOs were of higher initial diameter and exhibited higher microstructural order, see Figure 26.

4.7. Safe and Sustainable by Design

A safe-and-sustainable-by-design (SSbD) approach implies aiming to produce a CF-containing product that is inherently safe under all production, use and end-of-life scenarios, while still exhibiting the properties required for the intended use.

For SSbD, differences in the propensity to form WHO-fibers, such as between panCF 1 and 8, although their material properties are almost identical, should be considered as they may provide material selection-based strategies to minimize the risks associated with fiber-exposure. PanCF 15 is another example, as its material properties are similar to those of mPitchCF 14, with a drastically reduced propensity to form WHO-fiber fragments under the conditions studied. Interestingly, panCF 15 is distinguished by a relatively small initial diameter of 4.4 µm only.

4.8. Occupational Hygiene Aspects

Precautions against inhalation exposure to fiber dusts appear to be justified by the fiber pathogenicity paradigm (Pott and Friedrichs, 1972 [47]; Stanton and Wrench, 1972 [48]; Donaldson et al., 2010 [11]), which states that the elongated shape of fibers is a carcinogenic principle for respirable and biodurable fibers. Observed WHO-fibers, i.e., fibers longer than 5 µm, are currently considered to be sufficiently long to be toxicologically relevant and were used to rank the CF materials studied independently of fragment length.

In order to assess the propensity of a process to emit WHO-fibers, the number of formed respirable fragments must be related to the amount of carbon fiber processed, where the amount must be expressed in a practically useful metric. The filament length to be milled to a specific number of WHOFOs used in the first column of Table 7 is a metric that can make the number of observed WHOFOs intuitively accessible: It specifies the milled length of a single carbon fiber filament in millimeters that resulted in 10,000 WHOFOs. The chosen WHOFO number refers to the current German acceptance concentration for asbestos fibers in the workplace of 10,000 WHO-fibers/m³.

Hazardous dusts are only a source of potential occupational health risks if they are aerosolized and inhaled. For risk assessment, their emission rate, i.e., the amount of dust aerosolized per unit time, should be related to the efficiency of local ventilation, room air exchange or personal protective equipment. By considering our ball milling process as a hypothetical worst-case, an upper limit for the workplace aerosol concentration can be obtained: For a given filament processing rate and assuming complete emission of formed WHOFOs into the workplace atmosphere, the workplace air exchange rate and the effectiveness of the local ventilation or enclosure measures must be compared. This worst-case scenario can then be used to discuss, assess or investigate a real-world processing step: By what ratio is its WHOFO formation and emission rate lower? What process rate and duration, room volume and air exchange rate would be acceptable or necessary to keep the workplace concentration below the tolerance concentration?

A practical example could be the process of cutting a carbon textile structure with a tool of known cut width in order to prepare a reinforcement structure for a CFRP. Cutting a single 12k filament roving, with a cut width of only $10 \mu \mathrm{m}$ would result in 1200 mm of cut filament. The details of CF disintegration and of WHOFO formation will depend on the CF material and the cutting tool. Fragment exposure will depend on the ventilation and/or enclosure conditions. If structural disintegration of the cut CF volume were be as effective as ball milling, a single roving could be sufficient to contaminate 1 m³ of air volume with 10,000 WHO fibers even for the least critical panCF 15, and 100 times more for the most critical mPitchCF 11. Only at air exchange rates above the expected WHO-fiber formation rate can the fiber concentration be kept below the exposure limit.

4.9. Practical Relevance of CF Disintegration Testing by Ball Mill Grinding

Ball mill grinding was investigated using a commercial device and sealed containers as a practical and safe laboratory method to study intrinsic characteristics of CF disintegration. It facilitated the direct comparison of 9 different CF materials. Ball milling was found to involve mechanical failure pathways that lead to the formation of fragments with WHO-fiber morphology. The degree of CF disintegration achieved is to some extent adjustable by grinding time, ball number and mass, oscillation amplitude, frequency and amount of ground material. Here, the same milling conditions were applied to identical volumes of the studied CF materials in order to obtain a comparable energy impact per material volume. The chosen conditions resulted in a high degree of disintegration and are considered to be a worst-case scenario.

The impact of milling balls during the grinding of CF filaments in an oscillating mill can cause mechanical overload and lead to spallation products. Such high energy collision and friction processes impose various mechanical loading and shearing scenarios on a filament. The energy transfer from the grinding ball is multidirectional with respect to the fiber orientation and its anisotropic material properties, whereas standard machining processes such as abrasion, drilling or cutting act in a more directed manner along or perpendicular to a CF filament.

Ball milling must therefore be considered as a complex disintegration process. However, also the simplest mechanical failure scenarios for a single filament resulting from three-point bend or tensile testing to break are likewise highly complex processes: The applied high energy suddenly causes explosion-like disintegration and travelling shock waves that may provoke additional fractures along the filament [67,68]. Similar or even more complex mechanical overload and CF failure scenarios have to be considered for cutting or abrasive processing of CF composites due to different tool orientations and additional matrix-fiber interactions. In this respect, ball mill grinding can be considered as a simple but complex and therefore “all-inclusive” mechanical failure test.

For this first systematic study of CF disintegration, ball milling allowed the investigation of the CF fragmentation behavior under well-defined laboratory conditions. In this way, a relative ranking of the studied CF materials was obtained by classifying and counting fragments with properties relevant to the identification of potential health risks from respirable dusts [69]. It remains to be studied whether our ranking for the WHO fiber formation tendency obtained from ball mill testing correlates to that of encapsulated real-world machining laboratory setups or even to observations from workplace exposure measurements.

In all test situations, however, a common methodology of fragment morphology characterization should be applied. The present investigation exemplified how morphological fragmentation data can be compiled and correlated to material properties. Studies that investigate and rank the disintegration characteristics of different CF materials in real-world machining processes are currently underway.

5. Conclusions

This work contributes to the risk assessment of machined carbon fibers and their composites. It aims to support the development of safe-and-sustainable-by-design criteria.

Ball impact grinding of a given volume of fiber material in an oscillating mill under controlled conditions was used to assess the mechanical disintegration behavior of 9 different types of commercial carbon fibers. The resulting powders were homogeneously dispersed on track-etched membrane filters and imaged by SEM. The fragments formed were morphologically analyzed by trained personnel to provide data on their length, diameter, agglomeration state and fracture surface characteristics. These data allow the carbon fiber materials studied to be ranked according to their propensity to form fibrous and respirable fragments that meet the fiber counting conditions of the WHO.

Ball milling of carbon fibers was found to include mechanical failure modes leading to the formation of respirable fiber-shaped fragments. On-going work that applies the morphological fragment characterization and ranking methodology to real-world machining of carbon fibers and their composite materials will show whether ball mill grinding may serve as a simplified laboratory testing method with relevance for assessing carbon fiber type-related risk aspects of a wider range of processes.

Key findings of the present work include

• Not only mesophase pitch-based but also PAN-based carbon fibers can form WHO-fiber fragments in situations of mechanical overload. Such fibers are to be considered as potentially carcinogenic and require toxicological testing.
• The observed differences in the propensity of the PAN- and mesophase pitch-based CFs to form WHO-fibers, in terms of the volume of fiber milled, were smaller than previously reported in the literature; in most cases they were less than one order of magnitude.
• Earlier statements [38,64,65,66] that carbon fibers per se do not break in the direction of their fiber axis, do not form respirable fiber dusts and are therefore intrinsically safe have been disproved by this and more recent studies [7,43].
• Based on fragment surface analysis, the present work supports the assumption that the studied mesophase pitch-based CFs form fragments preferentially in the direction of the CF axis. However, such a disintegration pattern however did not systematically result in longer fragments, as mesophase pitch-based CF fragments tended to be thinner: Their higher tensile modulus values had only a small and insignificant effect on the aspect ratio of their fragments.

Safe-and-Sustainable-by-Design approaches for carbon fibers and their composites should take into account that

• For product designers unfamiliar with precursor-related material properties, the specific density data provided in the technical data sheet of a carbon fiber, could help to raise awareness of a potentially excessive propensity to form WHO-fiber fragments during mechanical disintegration. Densities above 1.95 g/cm³ are considered critical.
• A smaller initial carbon fiber diameter was observed to reduce the propensity to form fragments of WHO-fiber morphology: More fragments had the initial diameter as a result of fracturing transverse to the fiber axis. However, carbon fibers with a smaller initial diameter are likely to cause problems during recycling of polymer composite, as diameter thinning during pyrolysis processes brings such fibers closer to the respirable threshold. Such thinning can occur during the final pyrolysis stage where an oxygen-containing hot atmosphere is used to remove of polyaromatic hydrocarbon residues and soot.
• The mean diameter of the high-aspect-ratio-fragments formed is also an important characteristic as it can directly influence the number of fiber fragments formed: The thinner the mean fragment diameter, the more fragments can be formed from the same volume of disintegrated material. Two groups of materials have been proposed: The Low-Diameter (LDH) and High-Diameter (HDH) materials, containing carbon fiber types that formed mean fragment diameters below and above 2 µm, respectively. However, this criterion requires laborious microscopic evaluation of fragment morphologies.

In conclusion, at the current limited level of understanding of the carcinogenic potential of thin respirable carbon fibers, it appears irresponsible to neglect the potential release of fibrous respirable carbon fiber fragments during the processing, machining and recycling of CF-containing materials. According to the precautionary principle, unless the release is assessed under specific process and ventilation conditions, all related work activities must be accompanied by precautionary or, preferably, exposure-controlled safety measures to protect workers from biodurable respirable fiber exposure, following, e.g., a strategy as proposed in [34].

To reduce the workload for such workplace atmosphere assessments, automated dust imaging and particle shape recognition algorithms are being developed. Such techniques will also help to compile higher fragment statistics and facilitate future studies that include additional carbon fiber types and carbon fiber material machining scenarios. This is expected to further improve the understanding of correlations between material parameters and fragmentation behavior.