Method for the Analysis of Three-Phase Networks Containing Nonlinear Circuit Elements in View of an Efficient Power Flow Computation

Abstract

The present paper is devoted to applying the Hănțilă method for solving nonlinear three-phase circuits characterized by different reactance values on the three sequences (positive, negative and zero). Nonlinear elements, which are components of the circuit, are substituted by real voltage or current sources, whose values are an iteratively corrected function of the voltage across or the current through them, respectively. The analysis is carried out in the frequency domain and facilitates an easy evaluation of the power transfer on each harmonic. The paper presents numerical implementations of the method for two case studies. For validation, the results are compared against those obtained using the software LTspice in the time domain. Finally, the power flow on the harmonics and the overall power balance are analyzed.

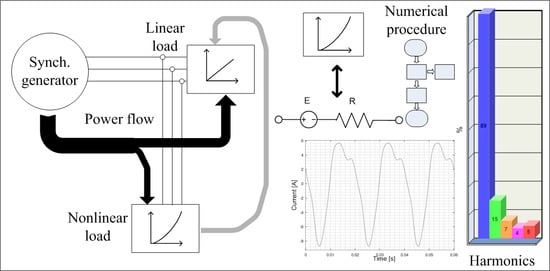
1. Introduction

Nonlinear circuit elements are an important source of harmonics in three-phase networks. Harmonics affect power quality and generate additional losses and overloads, may inflict operation malfunction, and finally significantly decrease the equipment’s life cycle or even cause its failure [1,2,3,4,5,6,7,8,9]. The current trend, both in the European Union and worldwide, is to reduce costs and increase the energy efficiency of both industrial and household equipment through the widespread use of power electronics [10,11,12,13]. Unfortunately, this approach is responsible for introducing harmonics into electrical power networks.

Reference [3] extensively details an analysis concerning the influence that voltage and current harmonics have on energy quality. Procedures are presented aiming for harmonic attenuation using passive and active filters, comprising controlled circuit elements. Measurement results complete and justify the performed analysis. A rich list of references comes to the aid of the reader who wants to deepen their knowledge in the field of energy quality. For efficient operation of the electric grids, the recurse to methods of analysis able to properly treat nonlinear circuits elements is essential for both evaluating their negative impact inflicted on the network and for projecting their positive action when active harmonic mitigation is envisaged.

Specialists have developed efficient software for solving time-periodic nonlinear circuits, in particular the asymptotic behavior method (in the time domain) and harmonic analysis (e.g., harmonic balance) [14,15]. However, there are some shortcomings of these methods. Unfortunately, the time-domain solution cannot take into account the different existing reactances of the synchronous generator for each of the three sequences. Moreover, the three-phase circuit is treated during solving as an ordinary circuit. More useful for solving three-phase circuits is the Harmonic Balance Method [14], which allows the linear part of the circuit to be solved by separating the circuit into symmetrical components—positive, negative and zero—substantially simplifying the complexity of the three-phase circuit. Unfortunately, all harmonics “meet” at the terminals of nonlinear elements, resulting in a huge system of nonlinear equations with a large number of unknowns. In fact, a hybrid time-frequency domain method is used: linear parts of the circuit are solved in the frequency domain and nonlinear in the time domain. Harmonic amplitudes intervene when the inverse Fourier transform is applied. Nonlinearity is usually treated by the Newton–Raphson method. However, there is no guarantee of convergence, and, as a result, sub-relaxation is envisaged. The computational effort is huge. The reduction of the computational burden proposed in [14,16,17,18,19,20] can be implemented by only retaining the first and most significant harmonics at the terminals of the nonlinear elements, which can be obtained through measurement. Behavioral frequency-domain models can be computed based on these nonlinear voltage–current relationship measurements. Other approaches have also been developed. For example, in [14], a comparison is conducted, under quasi-sinusoidal conditions, between different models: X-parameters, FTM models and simplified Volterra models. The main advantage of methods based on the Harmonic Balance model is the computation speed. The disadvantage mainly consists in the difficulty to generate a behavioral model that is close enough to the physical one. Moreover, the obtained results are not sufficiently accurate compared to the exact ones.

Three-phase circuits presenting nonlinear elements have been studied in numerous works, each highlighting the particularities of these circuits from different points of view. In that respect, important research on the circulation of power in such circuits was initiated by A. Țugulea, and further developed by a series of studies [21,22,23,24], to adapt the initial theory to the ever-increasing presence of nonlinear/distorting loads throughout the power grid.

An efficient method for solving resistive nonlinear circuits in the time-periodic regime was proposed by F. I. Hănțilă in [25] and concretized in [26,27,28]. Nonlinear elements are substituted by real voltage or current generators, in which the internal ideal sources are a corrected function of the voltage or the current at the terminals of equivalent real sources themselves. Applying this method for solving nonlinear three-phase networks was suggested in [23,29].

The present work focuses on applying the Hănțilă method capitalizing on its advantages for solving nonlinear three-phase circuits presenting different reactances on the three symmetrical components. The analysis is carried out in the frequency domain, thus allowing a direct and convenient evaluation of power transfer on each harmonic. Unlike [29], the present work contains illustrative numerical results, including power flow assessment. To illustrate the proposed approach, a simple circuit was chosen, as shown in Figure 1: a synchronous generator (Y connection), with different Fortescue sequence reactances, energizes the network through a three-phase rectifier (Y₀ connection).

The method is applicable for more complex three-phase circuits, which may contain unbalanced loads. The latter may be substituted by balanced loads and by non-symmetrical sources [29].

In order to validate the approach, we initially chose a circuit in which the internal reactance values of the generator were equal on all sequences. Then, the obtained results were compared to the data provided by solving the same circuit utilizing LTspice 17.0.31 software.

The following sections contain a short description of the method illustrated by its two instances, using the source’s voltage correction and the source’s current correction for the equivalent real source substituting the nonlinear elements. For the sake of simplicity, we will apply the method with uniport circuit elements. Evidently, the approach also holds for multi-port circuit elements [28].

Without any loss of generality, in our illustrative examples, we chose as nonlinear load a diode with i–u dependency, linearized by two semi-straight lines, characterized by the blocking resistance R_b and the conduction resistance R_c, respectively, as shown in Figure 2. We mention that the method can easily be adapted for the exponential characteristic of the diode. Additionally, the method can be utilized for other types of current–voltage dependencies of the nonlinear loads. The method can be also used for dependent nonlinear elements, e.g., thyristors.

2. Equivalent Source Voltage Correction

The method consists in substituting the nonlinear elements, with the characteristic

i = f(u),

(1)

with real voltage sources, comprising ideal voltage sources, whose emf is nonlinearly dependent, and internal resistances R (see Figure 3):

$$u=R i+e,$$

(2)

with

$$e=u-Rf\left(u\right)=g\left(u\right),$$

(3)

where i is the current through the nonlinear load and u is the voltage drop at its terminals.

Let us consider now the Hilbert space of periodical functions of period T. References [25,30] present in detail how resistance R must be chosen, such that function g is a contraction, if $q\in \left[0, 1\right)$ exists, such that

$$\parallel g\left(u_1\right)-g\left(u_2\right)\parallel \le q\parallel u_1-u_2\parallel \mathrm{for} \mathrm{each} u_1,u_2.$$

(4)

If (4) holds true for q = 1, then g(u) is non-expansive. The value of R must not be updated during iterations.

The property of function f being a Lipschitz function and a monotone one is necessary in order to obtain the contraction of function g, as presented in more detail in [25,26,27,28].

If q > 1, there is no contraction, and there is the possibility that the obtained iteration sequence is not a Picard–Banach one, and thus the procedure does not converge on the solution of the nonlinear circuit.

A linear circuit in a periodic regime is thus obtained. Through harmonic analysis, the circuit may be decomposed on a single phase and symmetrical components (Fortescue theorem). Then, the initial circuit shown in Figure 1 can be transformed to be solved under the form depicted in Figure 4. The source $\underset{\_}{E_{g_k}}$ resulting from the three-phase generator is nonzero only for the fundamental harmonic (of positive sequence).

If the circuit is balanced, the equivalent impedances of the phases are equal. At the terminals of the real voltage source equivalent to the nonlinear element, the rest of the circuit is connected. Let $\underset{\_}{U_k}$ be the voltage at the nonlinear element’s terminals, $\underset{\_}{I_k}$ the current through it, and $\underset{\_}{E_k}$ the emf of the source incorporating the nonlinear dependency, for each harmonic of rank k. We then have

$$\underset{\_}{U_k}=\underset{\_}{-I_k}\underset{\_}{Z_{e_k}}.$$

(5)

From Figure 4, we obtain

$$\underset{\_}{I_k}=-\left(\underset{\_}{E_k}+\underset{\_}{E_{g_k}}\right)/\left(\underset{\_}{Z_{e_k}}+R\right),$$

(6)

With (5) and (6), the voltage becomes

$$\underset{\_}{U_k}=\left(\underset{\_}{E_k}+\underset{\_}{E_{g_k}}\right)\underset{\_}{Z_{e_k}}/\left(\underset{\_}{Z_{e_k}}+R\right)=h_k\left(\underset{\_}{E_k}\right),$$

(7)

where $\underset{\_}{Z_{e_k}}$ is the equivalent impedance at the nonlinear load’s terminals, the value to compute for each harmonic frequency of rank k.

By using (7), it can easily be proven that $U_k=\left|h_k\left(\underset{\_}{E_k}\right)\right|\le$ $E_k$. Thus, the function h, through which the nonlinear element voltage vector $\underset{\_}{U}$ is determined (on the basis of the nonlinear equivalent voltage source vector $\underset{\_}{E}$), is always non-expansive, since $R\ge 0$.

Using the previously mentioned functions $g\left(u\right)$ and $h\left(\underset{\_}{E}\right)$, we have the following transformations:

$$u\stackrel{g}{\to }e \mathrm{in} \mathrm{the} \mathrm{time} \mathrm{domain};$$

(8)

$$\underset{\_}{E}\stackrel{h}{\to }\underset{\_}{U} \mathrm{in} \mathrm{the} \mathrm{frequency} \mathrm{domain}.$$

(9)

The solution of the iterative process describing the transition from step n to step n + 1, and implicitly from the time domain to the frequency domain and back again, can be represented as follows [29]:

$$e^{\left(n\right)}\stackrel{F}{\to }{\underset{\_}{E}}^{\left(n\right)}\stackrel{h}{\to }{\underset{\_}{U}}^{\left(n\right)}\stackrel{F^{-1}}{\to }{u}^{\left(n\right)}\stackrel{g}{\to }{e}^{\left(n+1\right)},$$

(10)

where:

• $e^{\left(n\right)}$—the equivalent voltage source of the nonlinear element at iteration n in the time domain;
• ${\underset{\_}{E}}^{\left(n\right)}$—the vector of complex phasors of the source harmonics $e^{\left(n\right)}$;
• ${\underset{\_}{U}}^{\left(n\right)}$—the vector of complex phasors of the voltage at the nonlinear element terminals;
• F—the Fourier transform;
• F⁻¹—the inverse Fourier transform.

To summarize, the nonlinear three-phase circuit solving method, when the equivalent sources voltages are corrected, can be described by the following steps:

• Nonlinear circuit elements are substituted with real sources whose ideal internal sources are dependent on the voltages at the terminals of the generators themselves (through function g).
• Circuits are defined for each harmonic and sequence in the complex.
• Having the time values of the equivalent sources (zero ones may be considered to start with), the harmonic spectrum of these equivalent sources is computed (using the Fourier series transform, F).
• The circuit is solved in complex, on each harmonic and sequence, and the complex voltages at the equivalent generators’ terminals are obtained (using function h).
• The time-domain values of voltages, previously determined at point 4, are computed (using the inverse Fourier series transform, F⁻¹).
• The equivalent sources voltages are corrected (via function g).

Remarks:

• The Fourier transform F is non-expansive when truncated to a finite number of terms [28];
• For the inverse Fourier transform F⁻¹, we take into account only the harmonics computed in the previous step of the iterative procedure.

All these aspects allow us to conclude that, within the iterative process, we have function h being non-expansive, function g being a contraction and Fourier transform also being non-expansive. The iterative procedure is thus a composition of non-expansive functions and a contraction, thus converging both in the frequency domain and in the time domain. Once the value of the nonlinearly controlled source is sufficiently accurately computed, the voltages and currents can also be determined for all the circuit elements of the network.

In the above-mentioned example, we took into consideration a single balanced three-phase nonlinear load, comprising identical diodes on each phase. Nonetheless, the approach is still valid if multiple nonlinear loads are present. The only modification that will appear in (6)—affecting also (7)—concerns the current $\underset{\_}{I_m{}_k}$, delivered by a given equivalent source, which will depend on the voltages $\underset{\_}{E_l{}_k}$ deduced for the other equivalent sources (through the transfer admittance matrix).

In the case of nonlinear circuit elements with dependent characteristics, (1) becomes i = f(u,t), with the current being dependent on time, not only on voltage, and the solving is otherwise identical to the previously presented one.

By taking into account the properties of the Picard–Banach sequences, the method allows establishing an upper bound for the distance (error) to the fixed-point—the exact solution—starting from the contraction factor and the distance between two successive iterations. The latter can be set as iteration stopping criterion [30]:

$$\parallel x^{*}-x^{\left(n\right)}\parallel ⩽\frac{1}{1-q}\parallel x^{\left(n+1\right)}-x^{\left(n\right)}\parallel ,$$

(11)

where $x^{*}$ is the fixed-point, q the contraction factor, and $x^{\left(n+1\right)}$ and $x^{\left(n\right)}$ the values obtained at iteration n + 1 and n, respectively.

3. Equivalent Source Current Correction

Solving the circuit, relying on the correction to the equivalent real source’s current, is dual to the approach discussed in Section 2. The nonlinear loads, with the characteristic

$$u=f^{-1}\left(i\right),$$

(12)

are substituted with real current sources, comprising an ideal current source i_s, nonlinearly controlled, and internal resistance R (see Figure 5), such that

$$i=i_s-u/R,$$

(13)

with

$$i_s=i+f^{-1}\left(i\right)/R=g_i\left(i\right).$$

(14)

As in Section 2, resistance R is chosen such that the function $g_i\left(i\right)$ is a contraction, in order to ensure that the iterative procedure converges [25]. Conveniently, value R must not be corrected during iterations. Furthermore, we define the function $h_i\left(\underset{\_}{I_s}\right)$, which is always non-expansive,

$$\underset{\_}{I_k}=h_{i_k}\left(\underset{\_}{I_{s_k}}\right)=\underset{\_}{(I_{s_k}}+\underset{\_}{I_{g_k}})R/\left(Z_{e_k}+R\right),$$

(15)

where $\underset{\_}{I_g{}_k}$ is the current of the sources accountable to the three-phase generator, on each frequency of rank k. In this particular case, the aforementioned complex current is nonzero only on the fundamental harmonic and the positive sequence.

Once the value of the current source (nonlinearly controlled, similar to Section 2) is sufficiently accurately determined, one can compute the currents and the voltages for all the elements of the circuit.

4. The Conservation of Complex Powers (Balance of Power)

The sources (e_ga, e_gb, e_gc), modeling the three-phase synchronous generator, deliver power to the network and also to the internal impedances, only on the fundamental frequency. The nonlinear load absorbs power on the fundamental and reinjects (delivers) a fraction of it through the nonlinearly controlled sources. On each harmonic, a separate balance of power is verified.

According to Tellegen’s theorem, conservation of powers (complex, active, reactive and instantaneous) is satisfied within an isolated network. Moreover, the terms of the Fourier transform form an orthonormal basis. Considering also the non-symmetry and residual (distorting) power theory put forward by Țugulea and the subsequent developments [21,22,23,24], the several instances of the balance of power on harmonics, and thus the negative influence of nonlinear loads, can be considered as evidence. These two types of active and reactive powers may naturally account for the parasitic power exchange within a network affected by nonlinearities and may provide useful information for predicting the unwanted power effects throughout a grid, subjected to distorted voltage and current waveforms.

At the fundamental frequency, the generator (e_ga, e_gb, e_gc) delivers complex power, and the other circuit elements, including the nonlinear sources, absorb power. The sum of the powers delivered on the fundamental is equal to the powers absorbed on the fundamental, without any harmonic cross-coupling effects. For the DC component and on the rest of the higher harmonics, the nonlinear elements always “deliver” non-symmetry and/or residual (distorting) (active and reactive), out of which a part is absorbed internally by the three-phase loads that include them, and the other part is absorbed by the other circuit elements/three-phase loads connected to the network [21]. Therefore, the recurse of voltage/current sources for the equivalence of nonlinear elements becomes even more convenient and naturally justified.

If multiple nonlinear loads are simultaneously present, the power exchange at the terminals of the nonlinear elements is not as straightforward as for a single such element present. In that case, some of them may “deliver” non-symmetry and/or residual active and reactive power and others may absorb them. In [21,22,23,24], any possible occurrence delivered/absorbed is demonstrated for a network (with or without neutral elements) comprising two three-phase loads, each having a nonlinear circuit element on phase 1. A balance of power may be globally verified for the nonlinear elements for each higher harmonic frequency: the powers “delivered” by them equals the sum of the absorbed powers (by linear or nonlinear elements) over that respective frequency.

A similar balance of power may be verified for each nonlinear element separately.

To conclude, a power-symmetrical generator is supposed to deliver power only on the fundamental harmonic and on the positive sequence. Any other power exchanges (DC and higher harmonic components and/or negative and zero sequences, for only the fundamental harmonic) occur as a result of the presence of nonlinear elements throughout the network. The powers (active and reactive according to Budeanu’s classical definition) accounting for these unwanted effects are termed residual (distorting) and non-symmetry, respectively. In a network containing a single distorting element, the latter will reinject (“deliver”) both residual (distorting) and non-symmetry active and reactive powers to the rest of the circuit. Should the network contain more than one nonlinear element, the aforementioned active and reactive powers may be transferred bidirectionally at the terminals of the distorting components. The actual transfer direction is finally imposed by the static i–u characteristic of each nonlinear element and can be evaluated in practice quantitatively by the use of efficient circuit analysis numerical methods, as proposed and carried out within this paper’s approach.

5. Illustrative Example 1—Cylindrical (Non-Salient) Pole Power Generator of Equal Reactances per Sequence

Let us solve the circuit shown in Figure 1 using the following values for the circuit elements: symmetrical power generator delivering voltages of amplitude 325 V at a frequency of 50 Hz, R₁ = 100 Ω, R_g = 0.5 Ω, R_s = 5 Ω, C₁ = 10 μF, C_s = 10 μF, L₁ = 5 mH, the i–u diode approximate static characteristic being defined by the blocking and conduction resistances R_b = 10⁵ Ω and R_c = 10 Ω (including the series conductor resistance), respectively. We assume, in this example, that there is a single value for the generator’s reactances on all the symmetrical sequences, namely that corresponding to the inductance L_g = 0.03 H.

5.1. Equivalent Source Voltage Correction Solution

Using the Hănțilă method, with its variant in which the voltage of the equivalent source is iteratively corrected—as presented in Section 2—starting from (3), the function $g\left(u\right)$ becomes:

$$e=g\left(u\right)=\{\begin{array}{c}u\left(R_c-R\right)/R_c\\ u\left(R_b-R\right)/R_b\end{array} \begin{array}{ccc}\mathrm{for}& u\ge 0& \\ \mathrm{for}& u<0.\end{array}$$

(16)

To ensure that $g\left(u\right)$ represents a contraction, $R_{ }\in \left(0, 2R_c\right)$. It can be noticed that a greater value for R ensures a better contraction factor and hence a more rapid convergence of the algorithm. By adopting $R_{ }=R_c=10 \mathsf{\Omega }$, (16) becomes

$$e_{ }=g\left(u_{ }\right)=\{\begin{array}{c}0\\ 0.9999 u\end{array}\begin{array}{ccc} & \mathrm{for}& u_{ }\ge 0\\ & \mathrm{for}& u_{ }<0.\end{array}$$

(17)

Let us consider the Fourier series truncated to its first 1000 harmonics. The method is flexible and allows truncating the Fourier series at a higher harmonic rank. The number of harmonics is a variable in our developed program, and it can thus be set according to the specific application. A greater number retained in the truncated series implies a better accuracy of the result, at the expense of computation time and increased volume of data. By doing so, we impose finding a solution to the initially set number of harmonics. By taking a sufficiently large number of harmonics so that the excluded ones’ significance is negligible, the obtained results are sufficiently close to the exact one. Normally, in practice, the equipment connected to the grid already incorporates technical solutions for filtering specific harmonics. In that sense, there are quite simple countermeasures to suppress the harmonics by a multiple of 2 (e.g., symmetrical static characteristics with respect to the origin, the use of bridge rectifiers, etc.) or even multiple of 3 (e.g., working neutral conductor elimination, the use of isolation transformers, etc.). In such cases, a significantly reduced number of harmonics may be considered (i.e., only one-third of them, when the series contains odd harmonics at a multiple of three), thus drastically diminishing the computational burden and, as a result, the overall processing time. It is worth mentioning that in our specific example, the computation was performed for all 1000 harmonics. The iterations are stopped when the distance (error) ε between two successive iterations is less than the imposed threshold of 10⁻⁸ V. The considered distance is defined in [30]:

$$\epsilon =| \underset{\_}{E^{\left(n\right)}}-\underset{\_}{E^{\left(n-1\right)}} |.$$

(18)

Analogously, a similar distance (error) can be defined in the time domain. The algorithm was implemented using GNU Octave 6.2.0. Equation (11) is used, a majorant of the distance, with respect to the resulting fixed point, namely 7.35 × 10 ⁻⁵ V. Due to the fact that several successive majorants have been applied, the actual distance is significantly smaller than the estimated one, and the result we might obtain is in fact significantly closer to the exact ideal one (the fixed point of the Picard–Banach sequence). We also point out that the above-mentioned errors are evaluated with respect to the result that would have been obtained considering the truncated number of harmonics we chose.

The emf voltage of the equivalent source corresponding to the nonlinear load is plotted in the time domain in Figure 6. The time-domain evolution of the voltage across the nonlinear circuit element is shown in Figure 7a. The graph, having a detailed view in Figure 7b, presents a voltage oscillation accountable to its abrupt drop—the Gibbs effect.

This effect can be mitigated by increasing the number of the considered harmonics and by reducing the value of the resistance R used for the computation. The downside is that both solutions generate an increase in the computation time.

Figure 8a,b shows the harmonic spectrum of the voltage across the nonlinear element shown in Figure 7a and its detail of Figure 7b. As mentioned above, once determined, the value of the equivalent source can be computed corresponding to the nonlinear element, all the other currents and voltages for the other circuit elements. Figure 9 shows the current time evolution through the nonlinear element. Figure 10 shows (a) the current through the generator of the network and (b) the current through inductance L₁.

5.2. Comparison of the Proposed Algorithm Results against LTspice Simulation Software

In this Subsection, we compare the results presented in Section 5.1 by utilizing the Hănțila method (implemented in GNU Octave) against the results obtained in the time domain by using the software package LTspice. In order to simulate the circuit utilizing the software LTspice, we used voltage-controlled current sources (Arbitrary Behavioral Current Source) to model the diodes. A time-domain procedure avoids the Gibbs effect. A similar problem appears as the voltage has a rapid variation even when the circuit is solved using the implicit settings of LTspice, no matter what computation solving module (trapezoidal, modified trap or Gear) is used. The error is diminished by imposing smaller computation tolerances, a smaller time-step, and by using the “alternate” solving option. All these settings options would significantly increase the computation time.

Let us compare, in the time domain, the results obtained utilizing the two methods for the voltage across the nonlinear element by taking their corresponding difference at the same time value. The maximal difference we obtained was 9.6744 V. The median value is 1.0732 × 10 ⁻² V, with a standard deviation (for the considered sample) of 0.4237 V. Important values for the difference between the results obtained through the two methods occur where the Gibbs effect is present. Figure 11a shows the superimposed time-domain graphs of the two methods (in the Gibbs effect zone) of the voltage across the nonlinear element. This allows us to conclude that only the aforementioned zone exhibits visible differences. To better illustrate the differences between the two results, we present Figure 10b, which shows the histogram of the above-mentioned voltage difference within the interval (–0.015 V, 0.015 V) containing 96.97% of the obtained values.

5.3. Power Computation and Validity Check—Balance of Powers

The software developed on the basis of the Hănțilă method allows us to compute the complex powers. In the same way, as presented in [21,22,23,24], the balance of complex powers may be verified for each harmonic: S_g, the complex power delivered by the sources of the generator; S_i, the complex power absorbed internally by the generator (including the line through components R_g and L_g); S_n, the complex power corresponding to the nonlinear load; and S_l, the complex power corresponding to the rest of the linear loads. The balances of powers are shown in

Table 1. Balance of complex powers for illustrative example 1 (equal reactances on symmetrical sequences). Note that the real part of the complex powers corresponds to the active power transfer (unit (W)) and the imaginary part corresponds to the reactive power transfer (unit (var)).

Harmonic Order	$\underset{\_}{{\mathit{S}}_{\mathit{g}}}$	$\underset{\_}{{\mathit{S}}_{\mathit{i}}}$	$\underset{\_}{{\mathit{S}}_{\mathit{n}}}$	$\underset{\_}{{\mathit{S}}_{\mathit{l}}}$	$\mathbf{Balance} \mathbf{of} \mathbf{Powers} \mathbf{for} \mathbf{Harmonics} \underset{\_}{{\mathit{S}}_{\mathit{g}}}$$+\underset{\_}{{\mathit{S}}_{\mathit{i}}}$$+\underset{\_}{{\mathit{S}}_{\mathit{n}}}$$+\underset{\_}{{\mathit{S}}_{\mathit{l}}}$
0—DC component		0	−1.1012 × 103	1.1012 × 103	0
1—fundamental	−3.1249 × 103 −2.2739 × 102j	3.0979 × 101 +5.8394 × 102j	1.5132 × 103 +1.1275 × 102j	1.5806 × 103 −4.6929 × 102j	−6.8212 × 10−13 +2.8422 × 10−13j
2		3.6912 +1.3916 × 102j	−3.0980 × 101 −1.2321 × 102j	2.7288 × 101 −1.5950 × 101j	−1.4211 × 10−14 −5.6843 × 10−14j
3		0	−5.4456 × 101 +4.6640 × 101j	5.4456 × 101 −4.6640 × 101j	−1.4211 × 10−14 +2.1316 × 10−14j
4		2.2478 × 10−2 +1.6948j	−7.7229 × 10−1 −8.7408 × 10−1j	7.4981 × 10−1 −8.2073 × 10−1j	−3.3307 × 10−16 −3.3307 × 10−16j
5		8.9241 × 10−2 +8.4107j	−5.2063 −1.7664j	5.1170 −6.6443j	0 +1.9984 × 10−15j
6		0	−2.7754 × 10−1 +4.0435 × 10−1j	2.7754 × 10−1 −4.0435 × 10−1j	−5.5511 × 10−17 −5.5511 × 10−17j
7		2.3962 × 10−3 +3.1617 × 10−1j	−3.5779 × 10−1 +2.3732 × 10−1j	3.5539 × 10−1 −5.5349 × 10−1j	−2.2204 × 10−16 +5.5511 × 10−17j
8		1.5097 × 10−3 +2.2765 × 10−1j	−3.5625 × 10−1 +3.3775 × 10−1j	3.5474 × 10−1 −5.6541 × 10−1j	1.6653 × 10−16 −1.6653 × 10−16j
9		0	−6.2792 × 10−3 +9.7711 × 10−3j	6.2792 × 10−3 −9.7711 × 10−3j	−1.7347 × 10−18 +0j
10		2.0533 × 10−4 +3.8704 × 10−2j	−1.2991 × 10−1 +1.4732 × 10−1j	1.2971 × 10−1 −1.8603 × 10−1j	8.3267 × 10−17 −5.5511 × 10−17j
…		…	…	…	…
999		0	−1.4358 × 10−15 −2.2189 × 10−9j	1.4358 × 10−15 +2.2189 × 10−9j	3.2312 × 10−27 +4.1359 × 10−25j
1000		1.9794 × 10−14 +3.7311 × 10−10j	−2.1239 × 10−14 −2.6122 × 10−9j	1.4446 × 10−15 +2.2391 × 10−9j	3.8774 × 10−26 −1.2408 × 10−24j
	Total $\underset{\_}{S_g}$ =	Total $\underset{\_}{S_i}$ =	Total $\underset{\_}{S_n}$ =	Total $\underset{\_}{S_l}$ =	Overall Balance of Powers $\underset{\_}{S_g}$+$\underset{\_}{S_i}$+$\underset{\_}{S_n}$+$\underset{\_}{S_l}$
Balance of powers for each network component (summing up all harmonic components)	−3.1249 × 103 −2.2739 × 102j	3.4786 × 101 +7.3380 × 102j	3.1932 × 102 +3.4637 × 101j	2.7707 × 103 −5.4105 × 102j	−7.1091 × 10−13 +2.5015 × 10−13j

, where the passive sign convention was used for the power computation: positive values represent absorbed (active/reactive) powers and negative values represent delivered (active/reactive) powers.

The results summarized in Table 1 are in total agreement with the principles stated in Section 4. The three-phase generator delivers complex power on the fundamental. Additionally, the three-phase loads absorb power on the fundamental. Part of it is internally absorbed, whereas the rest is reinjected into the rest of the network as delivered power via the harmonics. The differences corresponding to the verifications of the balance of powers (column 6) are in the order of the computation errors. Therefore, we conclude that the results are consistent with Tellegen’s theorem for complex power conservation.

It is worth pointing out that for the three-phase generator, there is no corresponding “internal” complex power S_i exchange (namely on R_g and L_g) for the DC and 0-sequence components in the absence of a neutral conductor linking the star points of the generator and of the nonlinear load, respectively.

An additional verification is obtained by performing the balance of complex powers for the nonlinear load; we obtain a remaining 3.1932 × 10² + 3.4637 × 10¹j value representing its “internal consumption”. The possible difference determined by summing up the powers delivered on the rest of the harmonics, whose rank exceeds 1000 (not taken into account as the result of the truncation) is totally negligible. Furthermore, an additional validation comes if we approximate the active power consumption of a diode with the power dissipated by R_c over all the considered harmonics; we obtain 3.1644 × 10² W, a value consistent with the above-determined remaining 3.1932 × 10² W value, resulting from the balance of verification of complex powers.

For the considered case study and the higher harmonics, the reactive power transfer is significantly more intense than that of the active power. Although the nonlinear charge has a purely resistive static characteristic, it transfers at its terminals not only active power but also reactive power. In the case of nonlinear loads and in the components of the considered network, it is also observed that, while the active power is unidirectional (nonlinear elements deliver power on the harmonics), the reactive power is bidirectional: for certain frequencies it is positive (absorbed power), and for some other is negative (delivered power), evidently after a fraction is consumed internally.

Table 1 summarizes the computed power values, not only for each harmonic component but also globally for the generators and the consumers. The definitive validation of the computation resides in the close to zero value of any balance of power check: for each harmonic, for each three-phase network component and, finally, for the entire circuit.

6. Illustrative Example 2—Salient Pole Power Generator of Different Reactances per Sequence

Let us consider now, for the second illustrative example of the salient pole generator, the case in which there are different sequence reactance values: for the fundamental harmonic $L_{g_f}=0.03 \mathrm{H}$ and for the other higher harmonics successions, equal values $L_{g_{DIH}}=5 \mathrm{mH}$. The rest of the circuit element values are the same as in Section 5.

6.1. Equivalent Source Voltage Correction Solution

The problem-solving method is similar to in Section 5.1. We maintain the first 1000 harmonics for truncating the Fourier series. Additionally, we chose R = R_c = 10 Ω. Iterations are halted when the distance between two successive steps is less than 10⁻⁸ V.

The voltage of the nonlinear load source is computed and plotted against time for the duration of one period, as shown in Figure 12a. The voltage drop across the nonlinear load is plotted vs. time in Figure 12b.

The Gibbs effect can once again be seen in Figure 13a,b, similarly as in Section 5.1. Once the value of the nonlinear source is computed, all the currents and the voltages of the other circuit elements may be also determined. Figure 14 shows the current through the nonlinear element.

Figure 15a shows the current through the network generator and Figure 15b shows the current through inductance L₁.

6.2. Comparison against LTspice Software Results

Solving the circuit in the time domain cannot take into consideration the different reactance values of the synchronous generator for the three sequences. A possible approximation, which only utilizes the fundamental reactance values, is not understood to provide sufficiently close results, as one can notice in Figure 7, Figure 9, Figure 10 and Figure 12, Figure 13, Figure 14 and Figure 15. Even though for the fundamental and the multiple-of-3 harmonics (zero sequence—as the result of the absence of the neutral toward the generator), the circuit impedances are the same, the differences for the other sequences (positive and negative) are enough to significantly alter the result. This aspect is noticeable even by comparing the balance of powers from Section 5.3 and Section 6.3, respectively.

Figure 16 shows the superimposed time evolution of the voltage across the nonlinear load for the two cases presented in Section 5.1 and Section 5.2.

6.3. Balance of Powers

Similar to Section 5.3, using the same notations, we verify the balance of powers for each complex harmonic frequency power and for each consumer connected to the network. The corresponding balances of powers are organized in

Table 2. Balance of complex powers for illustrative example 2 (different reactance values on symmetrical sequences for the fundamental and higher harmonics). Note that the real part of the complex powers corresponds to the active power transfer (unit (W)) and the imaginary part corresponds to the reactive power transfer (unit (var)).

Harmonic Order	$\underset{\_}{{\mathit{S}}_{\mathit{g}}}$	$\underset{\_}{{\mathit{S}}_{\mathit{i}}}$	$\underset{\_}{{\mathit{S}}_{\mathit{n}}}$	$\underset{\_}{{\mathit{S}}_{\mathit{l}}}$	$\mathbf{Balance} \mathbf{of} \mathbf{Powers} \mathbf{for} \mathbf{Harmonics} \underset{\_}{{\mathit{S}}_{\mathit{g}}}$$+\underset{\_}{{\mathit{S}}_{\mathit{i}}}$$+\underset{\_}{{\mathit{S}}_{\mathit{n}}}$$+\underset{\_}{{\mathit{S}}_{\mathit{l}}}$
DC component		0	−1.1823 × 103	1.1823 × 103	0
1—fundamental	−3.2226 × 103 −7.3492 × 101j	3.2790 × 101 +6.1807 × 102j	1.5776 × 103 −6.5922 × 101j	1.6122 × 103 −4.7866 × 102j	−2.2737 × 10−13 +1.4779 × 10−12j
2		3.1786 +1.9971 × 101j	−3.8473 −1.9581 × 101j	6.6880 × 10−1 −3.9091 × 10−1j	0
3		0	−4.5309 × 101 +3.8806 × 101j	4.5309 × 101 −3.8806 × 101j	−1.4211 × 10−14 +1.4211 × 10−14j
4		1.0834 × 10−01 +1.3615j	−2.0935 × 10−1 −1.2509j	1.0101 × 10−1 −1.1056 × 10−1j	4.4409 × 10−16 +4.4409 × 10−16j
5		2.3801 × 10−1 +3.7386j	−6.1859 × 10−1 −3.2444j	3.8058 × 10−1 −4.9417 × 10−1j	8.8818 × 10−16 −4.4409 × 10−16j
6		0	−2.8656 +4.1749j	2.8656 −4.1749j	8.8818 × 10−16 −8.8818 × 10−16j
7		3.9572 × 10−2 +8.7022 × 10−1j	−2.0293 × 10−1 −6.1581 × 10−1j	1.6336 × 10−1 −2.5442 × 10−1j	0 +3.3307 × 10−16j
8		7.6495 × 10−2 +1.9225j	−5.7656 × 10−1 −1.1255j	5.0007 × 10−1 −7.9704 × 10−1j	−2.2204 × 10−16 −8.8818 × 10−16j
9		0	−1.8838 × 10−1 +2.9313 × 10−1j	1.8838 × 10−1 −2.9313 × 10−1j	−1.6653 × 10−16 +5.5511 × 10−17j
10		4.0520 × 10−3 +1.2730 × 10−1j	−7.5223 × 10−2 −2.5223 × 10−2j	7.1171 × 10−2 −1.0207 × 10−1j	−6.9389 × 10−17 +7.6328 × 10−17j
...		...	...	...	...
999		0	−2.8261 × 10−15 −4.3674 × 10−9j	2.8261 × 10−15 +4.3674 × 10−9j	−1.1309 × 10−25 +8.2718 × 10−25j
1000		1.5573 × 10−12 +4.8925 × 10−9j	−1.5605 × 10−12 −9.7861 × 10−9j	3.1571 × 10−15 +4.8935 × 10−9j	2.8434 × 10−25 +3.3087 × 10−24j
	$\mathrm{Total} \underset{\_}{S_g}$ =	$\mathrm{Total} \underset{\_}{S_i}$ =	$\mathrm{Total} \underset{\_}{S_n}$ =	$\mathrm{Total} \underset{\_}{S_l}$ =	Overall balance of powers $\underset{\_}{S_g}$$+\underset{\_}{S_i}$$+\underset{\_}{S_n}$$+\underset{\_}{S_l}$
Balance of powers for each network component (summing up all harmonic components)	−3.2226 × 103 −7.3492 × 101j	3.6443 × 101 +6.4637 × 102j	3.4103 × 102 −4.8642 × 101j	2.8451 × 103 −5.2424 × 102j	−2.3970 × 10−13 +1.4909 × 10−12j

. By examining them, we confirm once again the conclusions drawn in Section 5.3.

We notice that a smaller reactance value for the symmetrical components influences the fundamental frequency results. There was a significant decrease in reactive power for the generator, compared to the case in Section 5.3, followed by an increase in the delivered active power.

7. Conclusions

The paper is devoted to applying the Hanțilă method for solving nonlinear three-phase circuits (in the frequency domain), which is further validated using a well-established time-domain circuit analysis package—LTspice. Power flow determinations are also possible as the final goal using the proposed approach. Moreover, LTspice (designed as a time-domain procedure) cannot be applied to synchronous three-phase generators presenting different internal reactances on sequences (+, −, 0). Our analysis is therefore essentially different from the one performed using LTspice. It relies on a Pichard–Banach sequence and makes use of advanced functional analysis (Hilbert spaces, fixed-point approach, contraction, etc.). Within the paper, we chose to compare the results against those provided by LTspice for the case of equal reactances on sequences.

The Hănțilă method for solving circuits comprising nonlinear loads is a useful algorithmic tool capable of providing evidence for the distorting effects inflicted by such consumers of three-phase networks. The method can easily be used even in the design stage in order to predict the distorting effect affecting the voltage and current waveforms, thereby enabling an accurate computation of the transferred powers in nonlinear three-phase networks. Eventually, it allows the implementation of the appropriate early-stage corrective measures.

The most important features of the method are the following:

• To our best knowledge, it is the only method that can be efficiently applied to nonlinear circuits, comprising three-phase generators presenting different sequence reactance values. In these cases, the inductances are a function of the rotor position; hence, they are also a function of time. This significantly complicates the time-domain analysis, besides the fact that the entire three-phase circuit must be solved.
• The circuit analysis is performed for each frequency harmonic.
• A single phase can be utilized for the three-phase circuit analysis. The method features an enormous computation effort in the case of large-scale circuits.
• We point out that the sources corresponding to the nonlinear elements are decomposed on positive, negative and zero sequences. Obviously, the computation time is reduced significantly. The most time-consuming software component is harmonic analysis. Nonetheless, in the context of the necessity of repeating this analysis during iterations, quantities $sin\left(k\omega t\right)$ and $cos\left(k\omega t\right)$ are determined only once at the beginning of the procedure (by reducing the argument in the first quadrant).
• The nonlinearity of the resistive circuit elements is taken into account only through the correction made to the equivalent sources’ values.
• Compared to the Harmonic Balance method, the presented method here has the advantage that convergence is always guaranteed without being necessary to recurse to under-relaxation. Moreover, the method even admits the use of over-relaxation. Compared to the Harmonic Balance Method the computation requires processing a smaller number of data, demanding less memory, and thus more harmonics may be considered in the analysis.
• Compared to the behavioral frequency-domain models, the presented method is more accurate, being based on a nonlinear time-domain characteristic, which is easier to determine and use. Moreover, it has the advantage of being able to process a significantly greater number of harmonics (at the user’s choice). The method presented in our paper may use a reduced number and/or a selection of harmonics (e.g., up to rank 25, or odd harmonics, which are not multiples of 3: 1, 5, 7, 11, 13, 17, 19, 23, 25), all by keeping a satisfactory degree of accuracy in a short computation time [28].
• It is also worth mentioning that the proposed method is equally efficient even when harmonic resonance is occurring on certain harmonics.
• Similar to all methods based on harmonic analysis, the proposed method is affected by the Gibbs effect, but the obtained result is sufficiently exact to a satisfactory degree.
• We mention that LTspice, one of the most efficient circuit analysis softwares, solves nonlinear circuits in the time domain, with the periodic regime solution being obtained through the symptotic behavior method (in the time domain). LTspice is unable to solve three-phase networks powered by generators exhibiting different sequence reactances. The internal inductances of the phases are coupled and time-dependent (upon the rotor’s position). LTspice cannot separate a single phase to perform the entire three-phase network analysis. Conversely, the time domain analysis avoids the Gibbs effect, which manifests itself when the present paper’s method is applied. That would represent a downside of the method.
• This paper’s method allows for easy complex-power computation and transfer throughout the network, for each circuit element, including the nonlinear elements, and permits identifying the harmonic frequencies where the circuit elements absorb power, as well as the ones they “deliver” power. The balance of powers (computed with the proposed algorithm) is in accordance with Tellegen’s theorem and confirms Țugulea’s power theory (and its subsequent developments), regarding the power flow in three-phase circuits affected by nonlinear elements. The generators of the network always deliver complex power only on the fundamental frequency and on positive sequences. Nonlinear loads (alongside linear ones) absorb power on the fundamental frequency. Part of the absorbed power is retained by the nonlinear elements, while the rest of the power is reinjected throughout the network as delivered power on the higher harmonics. Although apparently purely resistive, the nonlinear loads also absorb/deliver internally reactive power, not only active power.

For the proposed circuit, for the nonlinear loads, it can be noticed that, while the active power transfer is unidirectional, the distorting elements deliver active power on the harmonics and the reactive power transfer may be transferred in both directions: on certain harmonics it is positive and on others it is negative. For both kinds of powers, a part is retained internally by the nonlinear elements.

The method may by applied in a similar manner even for parametric nonlinear circuit elements. This extension of the theory will represent a subject of interest for our future work.