Analysis of Intrinsic Mechanistic of Stability-Tracking Control for Distributed Drive Autonomous Electric Vehicle
Abstract
:1. Introduction
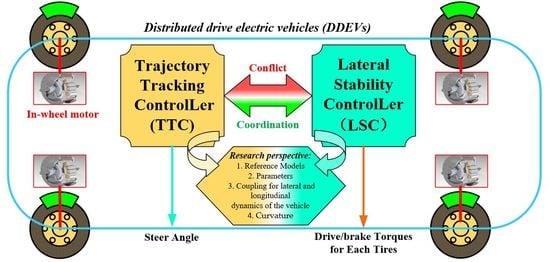
2. Stability-Tracking Hierarchical Control Structure
3. Analysis of the Interaction Process between Trajectory Tracking Control and Lateral Stability Control
3.1. Vehicle Dynamic Model
3.2. Trajectory Tracking Control Layer
3.3. Lateral Stability Control Layer
3.3.1. Steady-State Gain Model
3.3.2. Dynamic Response Model
3.4. An Intrinsic Mechanistic Framework for Stability-Tracking Control
4. Simulation Results and Analysis
4.1. Influence of Target Trajectory on Control System
4.2. Influence of Reference Model on Control System
4.3. Influence of Preview Time on the Control System
4.4. Influence of Stability Correction Coefficient on the Control System
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, Q.; Xie, Y.; Guo, S.; Bai, J.; Shu, Q. Sensing System of Environmental Perception Technologies for Driverless Vehicle: A Review of State of the Art and Challenges. Sens. Actuators A Phys. 2021, 319, 112566. [Google Scholar] [CrossRef]
- Wang, J.; Gao, S.; Wang, K.; Wang, Y.; Wang, Q. Wheel torque distribution optimization of four-wheel independent-drive electric vehicle for energy efficient driving. Control. Eng. Pract. 2021, 110, 104779. [Google Scholar] [CrossRef]
- Hang, P.; Chen, X. Towards Autonomous Driving: Review and Perspectives on Configuration and Control of Four-Wheel Independent Drive/Steering Electric Vehicles. Actuators 2021, 10, 184. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.Q.; Wang, Z.P.; Deng, J.J.; Dorrell, D.G. Chassis Coordinated Control for Full X-by-Wire Vehicles—A Review. Chin. J. Mech. Eng. 2021, 34, 1–25. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Y.Q.; Deng, Y.; Xu, H.; Deng, H.; Lin, F. Optimal Coordinated Control of ARS and DYC for Four-Wheel Steer and In-Wheel Motor Driven Electric Vehicle With Unknown Tire Model. IEEE Trans. Veh. Technol. 2020, 69, 10809–10819. [Google Scholar] [CrossRef]
- Nah, J.; Yim, S. Vehicle Stability Control with Four-Wheel Independent Braking, Drive and Steering on In-Wheel Motor-Driven Electric Vehicles. Electronics 2020, 9, 1934. [Google Scholar] [CrossRef]
- Ahangarnejad, A.H.; Radmehr, A.; Ahmadian, M. A review of vehicle active safety control methods: From antilock brakes to semiautonomy. J. Vib. Control. 2021, 27, 1683–1712. [Google Scholar] [CrossRef]
- Asiabar, A.N.; Kazemi, R. A direct yaw moment controller for a four in-wheel motor drive electric vehicle using adaptive sliding mode control. Proc. Inst. Mech. Eng. Part K-J. Multi-Body Dyn. 2019, 233, 549–567. [Google Scholar] [CrossRef]
- Zhang, X.; Goehlich, D.; Zheng, W. Karush-Kuhn-Tuckert based global optimization algorithm design for solving stability torque allocation of distributed drive electric vehicles. J. Frankl. Inst. -Eng. Appl. Math. 2017, 354, 8134–8155. [Google Scholar] [CrossRef]
- Zhuoping, Y.; Bo, L.; Lu, X.; Yuan, F.; Fenmiao, S. Direct Yaw Moment Control for Distributed Drive Electric Vehicle Handling Performance Improvement. Chin. J. Mech. Eng. 2016, 29, 486–497. [Google Scholar]
- Amer, N.H.; Zamzuri, H.; Hudha, K.; Kadir, Z.A. Modelling and Control Strategies in Path Tracking Control for Autonomous Ground Vehicles: A Review of State of the Art and Challenges. J. Intell. Robot. Syst. 2017, 86, 225–254. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Xiang, C.; Peng, H.; Wang, W.; Li, L.; An, Q.; Cheng, S. Path tracking coordinated control strategy for autonomous four in-wheel-motor independent-drive vehicles with consideration of lateral stability. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2021, 235, 1023–1036. [Google Scholar] [CrossRef]
- Liang, Y.; Li, Y.; Zheng, L.; Yu, Y.; Ren, Y. Yaw rate tracking-based path-following control for four-wheel independent driving and four-wheel independent steering autonomous vehicles considering the coordination with dynamics stability. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2021, 235, 260–272. [Google Scholar] [CrossRef]
- Wu, H.D.; Si, Z.L.; Li, Z.H. Trajectory Tracking Control for Four-Wheel Independent Drive Intelligent Vehicle Based on Model Predictive Control. IEEE Access 2020, 8, 73071–73081. [Google Scholar] [CrossRef]
- Hsu, L.Y.; Chen, T.L. An Optimal Wheel Torque Distribution Controller for Automated Vehicle Trajectory Following. IEEE Trans. Veh. Technol. 2013, 62, 2430–2440. [Google Scholar] [CrossRef]
- Wu, H.; Li, Z.; Si, Z. Trajectory tracking control for four-wheel independent drive intelligent vehicle based on model predictive control and sliding mode control. Adv. Mech. Eng. 2021, 13, 16878140211045142. [Google Scholar] [CrossRef]
- Guo, L.; Ge, P.; Yue, M.; Li, J. Trajectory tracking algorithm in a hierarchical strategy for electric vehicle driven by four independent in-wheel motors. J. Chin. Inst. Eng. 2020, 43, 807–818. [Google Scholar] [CrossRef]
- Li, B.Y.; Du, H.P.; Li, W.H. Trajectory control for autonomous electric vehicles with in-wheel motors based on a dynamics model approach. IET Intell. Transp. Syst. 2016, 10, 318–330. [Google Scholar] [CrossRef]
- Chen, J.; Shuai, Z.; Zhang, H.; Zhao, W. Path Following Control of Autonomous Four-Wheel-Independent-Drive Electric Vehicles via Second-Order Sliding Mode and Nonlinear Disturbance Observer Techniques. IEEE Trans. Ind. Electron. 2021, 68, 2460–2469. [Google Scholar] [CrossRef]
- Dai, P.; Katupitiya, J. Force control for path following of a 4WS4WD vehicle by the integration of PSO and SMC. Veh. Syst. Dyn. 2018, 56, 1682–1716. [Google Scholar] [CrossRef]
- Hu, C.; Wang, R.; Yan, F.; Nan, C. Output Constraint Control on Path Following of Four-Wheel Independently Actuated Autonomous Ground Vehicles. IEEE Trans. Veh. Technol. 2016, 65, 4033–4043. [Google Scholar] [CrossRef]
- Hussain, R.; Zeadally, S. Autonomous Cars: Research Results, Issues, and Future Challenges. IEEE Commun. Surv. Tutor. 2018, 21, 1275–1313. [Google Scholar] [CrossRef]
- Yao, Q.Q.; Tian, Y.; Wang, Q.; Wang, S.Y. Control Strategies on Path Tracking for Autonomous Vehicle: State of the Art and Future Challenges. IEEE Access 2020, 8, 161211–161222. [Google Scholar] [CrossRef]
- Zhang, J.X.; Zhou, S.Y.; Li, F.J.; Zhao, J. Integrated nonlinear robust adaptive control for active front steering and direct yaw moment control systems with uncertainty observer. Trans. Inst. Meas. Control. 2020, 42, 3267–3280. [Google Scholar] [CrossRef]
- Yin, D.; Wang, J.; Du, J.; Chen, G.; Hu, J.-S. A New Torque Distribution Control for Four-Wheel Independent-Drive Electric Vehicles. Actuators 2021, 10, 122. [Google Scholar] [CrossRef]
- Tian, Y.; Cao, X.; Wang, X.; Zhao, Y. Four wheel independent drive electric vehicle lateral stability control strategy. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 7, 1542–1554. [Google Scholar] [CrossRef]
- Dixit, S.; Fallah, S.; Montanaro, U.; Dianati, M.; Stevens, A.; McCullough, F.; Mouzakitis, A. Trajectory planning and tracking for autonomous overtaking: State-of-the-art and future prospects. Annu. Rev. Control. 2018, 45, 76–86. [Google Scholar] [CrossRef]
- Macadam, C.C. Application of an Optimal Preview Control for Simulation of Closed-Loop Automobile Driving. IEEE Trans. Syst. Man, Cybern. 1981, 11, 393–399. [Google Scholar] [CrossRef]
- Zhai, L.; Hou, R.; Sun, T.; Kavuma, S. Continuous Steering Stability Control Based on an Energy-Saving Torque Distribution Algorithm for a Four in-Wheel-Motor Independent-Drive Electric Vehicle. Energies 2018, 11, 350. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Chen, S.; Zhao, Y.; Gao, Z.; Li, C. Optimized Handling Stability Control Strategy for a Four In-Wheel Motor Independent-Drive Electric Vehicle. IEEE Access 2019, 7, 17017–17032. [Google Scholar] [CrossRef]
- Zhou, H.; Jia, F.; Jing, H.; Liu, Z.; Guvenc, L. Coordinated Longitudinal and Lateral Motion Control for Four Wheel Independent Motor-Drive Electric Vehicle. IEEE Trans. Veh. Technol. 2018, 67, 3782–3790. [Google Scholar] [CrossRef]


















| Symbol | Description | Value |
|---|---|---|
| m | Vehicle mass (kg) | 1830 |
| vx, vy | Longitudinal and lateral velocity (km/h) | - |
| lf, lr | Distance from center mass to front and rear axle (m) | 1.4, 1.6 |
| l | Distance from front axle to rear axle (m) | |
| d | half of the vehicle front and rear track widths (m) | 1.6 |
| hg | Height of center mass (m) | 0.5 |
| kfl, kfr, krl, krr | Cornering stiffness of four tires (N/rad) | - |
| αfr, αfr, αrl, αrr | Slip angle of four tires (rad) | - |
| β | Sideslip angle of vehicle (rad) | - |
| g | Acceleration of gravity (m/s2) | 9.8 |
| γ | Yaw rate of the sprung mass of the tractor (rad/s) | - |
| IZ | Yaw moment of inertia of center mass (kg·m2) | 3655.4 |
| m | Vehicle mass (kg) | 1830 |
| Parameters | TiT | TdT | KT | Ti | Td | p |
|---|---|---|---|---|---|---|
| Value | 4 | 0.05 | 800 | 2 | 0.1 | 0.7 |
| Peak Values | DYC | R = 60 m | R = 80 m | R = 100 m |
|---|---|---|---|---|
| ΔYmax (m) | Ks = 0 (No DYC) | 6.26 | 0.02 | 0.03 |
| Ks = 400 | 3.06 | 0.07 | 0.08 |
| Peak Values | 1-OSSGM, τ = 0.5 | 1-OSSGM, τ = 1 | L2-DOFM, TPS = 0.8 s | NS-SSGM | OS-SSGM | US-SSGM |
|---|---|---|---|---|---|---|
| ΔYmax (m), near X = 100 | 0.63 | 1.10 | 0.18 | 0.18 | 0.13 | 0.32 |
| ΔYmax (m), near X = 150 | 0.38 | 1.47 | 0.21 | 0.21 | 0.17 | 0.39 |
| δmax (deg) | 93.3 | 143.9 | 40.7 | 40.7 | 25.4 | 84.8 |
| Peak Values | TPT = 0.6 s | TPT = 0.8 | TPT = 1.0 s | TPT = 1.2 s | TPT = 1.4 s |
|---|---|---|---|---|---|
| ΔYmax (m), near X = 100 | 0.61 | 0.28 | 0.21 | 0.16 | 0.05 |
| ΔYmax (m), near X = 150 | 0.47 | 0.31 | 0.24 | 0.26 | 0.31 |
| δmax (deg) | 166.9 | 54.8 | 41.1 | 36.4 | 32.1 |
| Peak Values | KS = 0 (NO DYC) | KS = 100 | KS = 200 | KS = 400 | KS = 800 | KS = 1600 |
|---|---|---|---|---|---|---|
| ΔYmax (m), near X = 100 | 0.27 | 0.23 | 0.20 | 0.18 | 0.17 | 0.19 |
| ΔYmax (m), near X = 150 | 0.31 | 0.27 | 0.24 | 0.22 | 0.20 | 0.23 |
| δmax (deg) | 55.1 | 48.9 | 44.8 | 42.4 | 40.6 | 40.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, X.; Yan, Y.; Wang, B.; Xu, X.; Zhang, L. Analysis of Intrinsic Mechanistic of Stability-Tracking Control for Distributed Drive Autonomous Electric Vehicle. Electronics 2021, 10, 3010. https://doi.org/10.3390/electronics10233010
Tang X, Yan Y, Wang B, Xu X, Zhang L. Analysis of Intrinsic Mechanistic of Stability-Tracking Control for Distributed Drive Autonomous Electric Vehicle. Electronics. 2021; 10(23):3010. https://doi.org/10.3390/electronics10233010
Chicago/Turabian StyleTang, Xuequan, Yunbing Yan, Baohua Wang, Xiaowei Xu, and Lin Zhang. 2021. "Analysis of Intrinsic Mechanistic of Stability-Tracking Control for Distributed Drive Autonomous Electric Vehicle" Electronics 10, no. 23: 3010. https://doi.org/10.3390/electronics10233010
APA StyleTang, X., Yan, Y., Wang, B., Xu, X., & Zhang, L. (2021). Analysis of Intrinsic Mechanistic of Stability-Tracking Control for Distributed Drive Autonomous Electric Vehicle. Electronics, 10(23), 3010. https://doi.org/10.3390/electronics10233010