Privacy-Enhanced Federated Learning: A Restrictively Self-Sampled and Data-Perturbed Local Differential Privacy Method
Abstract
:1. Introduction
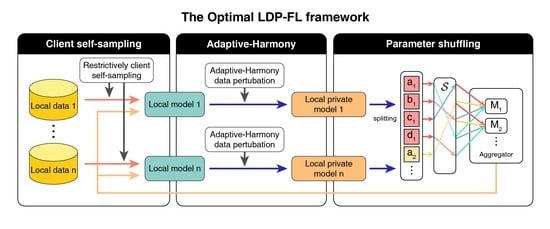
- We propose a novel LDP-FL, which integrates an efficiency-optimized data perturbation and a parameter-shuffling mechanism, and client self-sampling technology in the federated learning process to improve model utility and reduce communication costs, ensuring privacy.
- We propose an efficiency-optimized data perturbation algorithm, which supports perturbing parameter adaptive selection and minimum parameter transmission to hold the advanced asymptotic error boundary and improve communication efficiency.
- We propose restrictive client self-sampling technology which limits the range of self-sampling probability to a more reasonable one to improve the utility.
- We verify our method’s efficiency, privacy, and performance from theoretical and practical aspects. We analyze the asymptotic error boundary and communication cost and prove that our unbiased algorithm satisfies LDP. We also evaluate our algorithm on multiple databases from the utility, privacy budget, and communication cost standpoints.
2. Background and Related Works
2.1. Federated Learning
2.2. Differential Privacy
2.3. Data Perturbation in LDP
2.4. Privacy Amplification
3. Optimal LDP-FL
3.1. Outline
3.1.1. Local Update
3.1.2. Global Update
3.2. Adaptive-Harmony
3.2.1. Adaptive-Duchi
| Algorithm 1: Optimal LDP-FL |
 |
3.2.2. Adaptive-Harmony
| Algorithm 2: Adaptive-Harmony |
 |
3.3. Parameter Shuffling
| Algorithm 3: Parameter Shuffling |
 |
3.4. Restrictive Client Self-Sampling
- There exists an optimal that renders an optimal performance, since in an FL system with m clients, there is the optimal number of participating clients x which optimizes the performance. Therefore, for , there is an optimal range that guarantees the best convergence and model accuracy.
- When the number of participants approaches all participants, the performance is optimal. Therefore, the optimal FL model performance (i.e., convergence and model accuracy) can be achieved when restricting the optimal range to .
| Algorithm 4: Restrictive Self-Sampling |
 |
4. Utility Analysis
4.1. Privacy Analysis
4.2. Utility Analysis
5. Evaluation
5.1. Experimental Setting
5.2. Utility Evaluation
5.2.1. Model Accuracy vs. Number of Clients
5.2.2. Model Accuracy vs. Privacy Budget
5.3. Efficiency Evaluation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| FL | Federated learning |
| DP | Differential privacy |
| CDP | Centralized differential privacy |
| LDP | Local differential privacy |
| LDP-FL | Federated learning with LDP |
| FedSGD | Federated stochastic gradient descent |
| LAD | Latent Dirichlet allocation |
| FedAvg | Federated averaging |
References
- Pouyanfar, S.; Sadiq, S.; Yan, Y.; Tian, H.; Tao, Y.; Reyes, M.P.; Shyu, M.L.; Chen, S.C.; Iyengar, S.S. A survey on deep learning: Algorithms, techniques, and applications. ACM Comput. Surv. (CSUR) 2018, 51, 1–36. [Google Scholar] [CrossRef]
- Deng, W.; Zhang, L.; Zhou, X.; Zhou, Y.; Sun, Y.; Zhu, W.; Chen, H.; Deng, W.; Chen, H.; Zhao, H. Multi-strategy particle swarm and ant colony hybrid optimization for airport taxiway planning problem. Inf. Sci. 2022, 612, 576–593. [Google Scholar] [CrossRef]
- Song, Y.; Cai, X.; Zhou, X.; Zhang, B.; Chen, H.; Li, Y.; Deng, W.; Deng, W. Dynamic hybrid mechanism-based differential evolution algorithm and its application. Expert Syst. Appl. 2023, 213, 118834. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, P.; Zhang, R.; Yao, R.; Deng, W. A novel performance trend prediction approach using ENBLS with GWO. Meas. Sci. Technol. 2022, 34, 025018. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.; Liu, Y.; Deng, W.; Deng, W. Co-evolutionary competitive swarm optimizer with three-phase for large-scale complex optimization problem. Inf. Sci. 2023, 619, 2–18. [Google Scholar] [CrossRef]
- Trask, A.W. Grokking Deep Learning; Simon and Schuster: New York, NY, USA, 2019. [Google Scholar]
- Deng, W.; Xu, J.; Gao, X.; Zhao, H. An Enhanced MSIQDE Algorithm with Novel Multiple Strategies for Global Optimization Problems. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1578–1587. [Google Scholar] [CrossRef]
- Jin, T.; Zhu, Y.; Shu, Y.; Cao, J.; Yan, H.; Jiang, D. Uncertain optimal control problem with the first hitting time objective and application to a portfolio selection model. J. Intell. Fuzzy Syst. 2022, 1–15, in press. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated machine learning: Concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 2019, 10, 1–19. [Google Scholar] [CrossRef]
- Shi, W.; Cao, J.; Zhang, Q.; Li, Y.; Xu, L. Edge computing: Vision and challenges. IEEE Internet Things J. 2016, 3, 637–646. [Google Scholar] [CrossRef]
- Chen, J.; Ran, X. Deep learning with edge computing: A review. Proc. IEEE 2019, 107, 1655–1674. [Google Scholar] [CrossRef]
- Wu, X.; Liang, Z.; Wang, J. FedMed: A Federated Learning Framework for Language Modeling. Sensors 2020, 20, 4048. [Google Scholar] [CrossRef] [PubMed]
- Mills, J.; Hu, J.; Min, G. Communication-efficient federated learning for wireless edge intelligence in IoT. IEEE Internet Things J. 2019, 7, 5986–5994. [Google Scholar] [CrossRef] [Green Version]
- Khan, L.U.; Saad, W.; Han, Z.; Hossain, E.; Hong, C.S. Federated learning for internet of things: Recent advances, taxonomy, and open challenges. IEEE Commun. Surv. Tutor. 2021, 23, 1759–1799. [Google Scholar] [CrossRef]
- Jin, T.; Gao, S.; Xia, H.; Ding, H. Reliability analysis for the fractional-order circuit system subject to the uncertain random fractional-order model with Caputo type. J. Adv. Res. 2021, 32, 15–26. [Google Scholar] [CrossRef]
- Liu, Y.; Qu, Y.; Xu, C.; Hao, Z.; Gu, B. Blockchain-Enabled Asynchronous Federated Learning in Edge Computing. Sensors 2021, 21, 3335. [Google Scholar] [CrossRef]
- Mohassel, P.; Zhang, Y. Secureml: A system for scalable privacy-preserving machine learning. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–24 May 2017; pp. 19–38. [Google Scholar]
- Asad, M.; Moustafa, A.; Yu, C. A Critical Evaluation of Privacy and Security Threats in Federated Learning. Sensors 2020, 20, 7182. [Google Scholar] [CrossRef]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Proceedings of the Theory of Cryptography Conference, New York, NY, USA, 4–7 May 2006; pp. 265–284. [Google Scholar]
- Dwork, C.; Feldman, V.; Hardt, M.; Pitassi, T.; Reingold, O.; Roth, A.L. Preserving statistical validity in adaptive data analysis. In Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, Portland, OR, USA, 14–17 June 2015; pp. 117–126. [Google Scholar]
- Ziller, A.; Trask, A.; Lopardo, A.; Szymkow, B.; Wagner, B.; Bluemke, E.; Nounahon, J.M.; Passerat-Palmbach, J.; Prakash, K.; Rose, N.; et al. Pysyft: A library for easy federated learning. In Federated Learning Systems; Springer: Berlin, Germany, 2021; pp. 111–139. [Google Scholar]
- Hesamifard, E.; Takabi, H.; Ghasemi, M.; Wright, R.N. Privacy-preserving machine learning as a service. Proc. Priv. Enhancing Technol. 2018, 2018, 123–142. [Google Scholar] [CrossRef] [Green Version]
- Ryffel, T.; Trask, A.; Dahl, M.; Wagner, B.; Mancuso, J.; Rueckert, D.; Passerat-Palmbach, J. A generic framework for privacy preserving deep learning. arXiv 2018, arXiv:1811.04017. [Google Scholar]
- Wang, T.; Zhang, X.; Feng, J.; Yang, X. A Comprehensive Survey on Local Differential Privacy toward Data Statistics and Analysis. Sensors 2020, 20, 7030. [Google Scholar] [CrossRef]
- Truex, S.; Liu, L.; Chow, K.H.; Gursoy, M.E.; Wei, W. LDP-Fed: Federated learning with local differential privacy. In Proceedings of the Third ACM International Workshop on Edge Systems, Analytics and Networking, Heraklion, Greece, 27 April 2020; pp. 61–66. [Google Scholar]
- Li, J.; Khodak, M.; Caldas, S.; Talwalkar, A. Differentially private meta-learning. arXiv 2019, arXiv:1909.05830. [Google Scholar]
- Wang, Y.; Tong, Y.; Shi, D. Federated latent Dirichlet allocation: A local differential privacy based framework. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2020; Volume 34, pp. 6283–6290. [Google Scholar]
- Bhowmick, A.; Duchi, J.; Freudiger, J.; Kapoor, G.; Rogers, R. Protection against reconstruction and its applications in private federated learning. arXiv 2018, arXiv:1812.00984. [Google Scholar]
- Liu, R.; Cao, Y.; Yoshikawa, M.; Chen, H. Fedsel: Federated sgd under local differential privacy with top-k dimension selection. In Proceedings of the International Conference on Database Systems for Advanced Applications, Jeju, Korea, 24–27 September 2020; pp. 485–501. [Google Scholar]
- Cao, T.; Huu, T.T.; Tran, H.; Tran, K. A federated deep learning framework for privacy preservation and communication efficiency. J. Syst. Archit. 2022, 124, 102413. [Google Scholar] [CrossRef]
- McMahan, H.B.; Moore, E.; Ramage, D.; y Arcas, B.A. Federated learning of deep networks using model averaging. arXiv 2016, arXiv:1602.05629. [Google Scholar]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Minimax optimal procedures for locally private estimation. J. Am. Stat. Assoc. 2018, 113, 182–201. [Google Scholar] [CrossRef]
- Nguyên, T.T.; Xiao, X.; Yang, Y.; Hui, S.C.; Shin, H.; Shin, J. Collecting and analyzing data from smart device users with local differential privacy. arXiv 2016, arXiv:1606.05053. [Google Scholar]
- Wang, N.; Xiao, X.; Yang, Y.; Zhao, J.; Hui, S.C.; Shin, H.; Shin, J.; Yu, G. Collecting and analyzing multidimensional data with local differential privacy. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macau, China, 8–11 April 2019; pp. 638–649. [Google Scholar]
- Sun, L.; Qian, J.; Chen, X. Ldp-fl: Practical private aggregation in federated learning with local differential privacy. arXiv 2020, arXiv:2007.15789. [Google Scholar]
- Balle, B.; Bell, J.; Gascón, A.; Nissim, K. The privacy blanket of the shuffle model. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2019; pp. 638–667. [Google Scholar]
- Cheu, A.; Smith, A.; Ullman, J.; Zeber, D.; Zhilyaev, M. Distributed differential privacy via shuffling. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, 30 May–3 June 2019; pp. 375–403. [Google Scholar]
- Erlingsson, Ú.; Feldman, V.; Mironov, I.; Raghunathan, A.; Talwar, K.; Thakurta, A. Amplification by shuffling: From local to central differential privacy via anonymity. In Proceedings of the Thirtieth Annual ACM-SIAM Symposium on Discrete Algorithms, San Diego, CA, USA, 6–9 January 2019; pp. 2468–2479. [Google Scholar]
- Girgis, A.M.; Data, D.; Diggavi, S. Differentially private federated learning with shuffling and client self-sampling. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Melbourne, VIC, Australia, 12–20 July 2021; pp. 338–343. [Google Scholar]
- Wei, K.; Li, J.; Ding, M.; Ma, C.; Yang, H.H.; Farokhi, F.; Jin, S.; Quek, T.Q.S.; Poor, H.V. Federated Learning with Differential Privacy: Algorithms and Performance Analysis. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3454–3469. [Google Scholar] [CrossRef] [Green Version]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 9–11 May 2017; pp. 1273–1282. [Google Scholar]
- Kasiviswanathan, S.P.; Lee, H.K.; Nissim, K.; Raskhodnikova, S.; Smith, A. What can we learn privately? SIAM J. Comput. 2011, 40, 793–826. [Google Scholar] [CrossRef]
- Choudhury, O.; Gkoulalas-Divanis, A.; Salonidis, T.; Sylla, I.; Park, Y.; Hsu, G.; Das, A. Differential privacy-enabled federated learning for sensitive health data. arXiv 2019, arXiv:1910.02578. [Google Scholar]
- Jayaraman, B.; Evans, D. When relaxations go bad: “differentially-private” machine learning. arXiv 2019, arXiv:1902.08874. [Google Scholar]
- Zhao, Y.; Zhao, J.; Yang, M.; Wang, T.; Wang, N.; Lyu, L.; Niyato, D.; Lam, K.Y. Local differential privacy-based federated learning for internet of things. IEEE Internet Things J. 2020, 8, 8836–8853. [Google Scholar] [CrossRef]
- Lian, Z.; Wang, W.; Su, C. COFEL: Communication-Efficient and Optimized Federated Learning with Local Differential Privacy. In Proceedings of the ICC 2021-IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Warner, S.L. Randomized response: A survey technique for eliminating evasive answer bias. J. Am. Stat. Assoc. 1965, 60, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Local privacy and statistical minimax rates. In Proceedings of the 2013 IEEE 54th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 26–29 October 2013; pp. 429–438. [Google Scholar]
- Beimel, A.; Brenner, H.; Kasiviswanathan, S.P.; Nissim, K. Bounds on the sample complexity for private learning and private data release. Mach. Learn. 2014, 94, 401–437. [Google Scholar] [CrossRef] [Green Version]
- Girgis, A.M.; Data, D.; Diggavi, S.; Kairouz, P.; Suresh, A.T. Shuffled model of federated learning: Privacy, communication and accuracy trade-offs. arXiv 2020, arXiv:2008.07180. [Google Scholar] [CrossRef]
- Bittau, A.; Erlingsson, Ú.; Maniatis, P.; Mironov, I.; Raghunathan, A.; Lie, D.; Rudominer, M.; Kode, U.; Tinnes, J.; Seefeld, B. Prochlo: Strong privacy for analytics in the crowd. In Proceedings of the 26th Symposium on Operating Systems Principles, Shanghai, China, 28 October 2017; pp. 441–459. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Yang, M.; Zhang, R.; Song, W.; Zheng, J.; Feng, J.; Matwin, S. Privacy-Enhanced Federated Learning: A Restrictively Self-Sampled and Data-Perturbed Local Differential Privacy Method. Electronics 2022, 11, 4007. https://doi.org/10.3390/electronics11234007
Zhao J, Yang M, Zhang R, Song W, Zheng J, Feng J, Matwin S. Privacy-Enhanced Federated Learning: A Restrictively Self-Sampled and Data-Perturbed Local Differential Privacy Method. Electronics. 2022; 11(23):4007. https://doi.org/10.3390/electronics11234007
Chicago/Turabian StyleZhao, Jianzhe, Mengbo Yang, Ronglin Zhang, Wuganjing Song, Jiali Zheng, Jingran Feng, and Stan Matwin. 2022. "Privacy-Enhanced Federated Learning: A Restrictively Self-Sampled and Data-Perturbed Local Differential Privacy Method" Electronics 11, no. 23: 4007. https://doi.org/10.3390/electronics11234007
APA StyleZhao, J., Yang, M., Zhang, R., Song, W., Zheng, J., Feng, J., & Matwin, S. (2022). Privacy-Enhanced Federated Learning: A Restrictively Self-Sampled and Data-Perturbed Local Differential Privacy Method. Electronics, 11(23), 4007. https://doi.org/10.3390/electronics11234007