Deep Reinforcement Learning-Based Adaptive Beam Tracking and Resource Allocation in 6G Vehicular Networks with Switched Beam Antennas

Abstract

In this paper, we propose a novel switched beam antenna system model integrated with deep reinforcement learning (DRL) for 6G vehicle-to-vehicle (V2V) communications. The proposed system model aims to address the challenges of highly dynamic V2V environments, including rapid changes in channel conditions, interference, and Doppler effects. By leveraging the beam-switching capabilities of switched beam antennas and the intelligent decision making of DRL, the proposed approach enhances the performance of 6G V2V communications in terms of throughput, latency, reliability, and spectral efficiency. The proposed work develops a comprehensive mathematical model that accounts for 6G channel modeling, beam-switching, and beam-alignment errors. The Proposed DRL framework is designed to learn optimal beam-switching decisions in real time, adapting to the complex and varying V2V communication scenarios. The integration of the proposed antenna system and DRL model results in a robust solution that is capable of maintaining reliable communication links in a highly dynamic environment. To validate the proposed approach, extensive simulations were conducted and performance analysis using various performance metrics, such as throughput, latency, reliability, energy efficiency, resource utilization, and network scalability, was analyzed. Results demonstrate that the proposed system model significantly outperforms conventional V2V communication systems and other state-of-the-art techniques. Furthermore, the proposed approach shows that the beam-switching capabilities of the switched beam antenna system and the intelligent decision making of the DRL model are essential in addressing the challenges of 6G V2V communications.

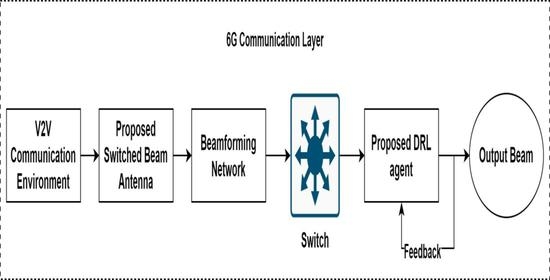
1. Introduction

The rapid advancements in wireless communication technologies and the proliferation of connected devices have led to the development of next-generation communication systems, such as the sixth-generation (6G) networks [1]. These networks are envisioned to provide unprecedented data rates, ultra-reliable low-latency communication (URLLC), and seamless connectivity, enabling various emerging applications, such as autonomous vehicles, smart cities, and the Internet of Things (IoT). In the context of vehicular communications, 6G networks play a crucial role in providing robust and high-performance vehicle-to-vehicle (V2V) and vehicle-to-everything (V2X) connections, which are essential for enabling safety-critical applications, such as collision avoidance and cooperative driving [2].

One of the key enablers of high-performance V2V communication in 6G networks is the utilization of advanced antenna technologies, such as switched beam antennas. Switched beam antennas offer the capability to dynamically adjust their radiation patterns, enabling them to maintain an optimal beam alignment in the rapidly changing vehicular environment. This adaptive beam tracking capability is crucial for ensuring reliable and low-latency communication links, which are essential for safety-critical vehicular applications [3].

However, the design and optimization of switched beam antennas for 6G V2V communication systems pose several challenges, including the need to account for the unique propagation characteristics of Terahertz frequency bands and the ultradense deployment of communication devices. Moreover, real-time adaptation of beam tracking and resource allocation strategies is required to meet the stringent latency and reliability requirements of 6G vehicular networks.

To address these challenges, the conducted study proposes a deep reinforcement learning (DRL)-based adaptive beam tracking and resource allocation framework for 6G V2V communication systems with switched beam antennas. The proposed framework combines the strengths of DRL, which enables learning optimal control policies in complex and dynamic environments, with the adaptability of switched beam antennas, to achieve robust and high-performance V2V communication links. This paper presents a comprehensive system model that incorporates key 6G insights, such as terahertz communication and ultra-reliable low-latency communication (URLLC), as well as the unique features of switched beam antennas. The proposed work develops a DRL-based beam tracking and resource allocation model that adapts to the rapidly changing V2V environment, ensuring optimal beam alignment and resource utilization. It is also a provided advanced mathematical analysis of the proposed system model, focusing on the role of switched beam antennas in enhancing the performance of 6G V2V communications. A list of acronyms used in this study is shown in

Table 1. List of acronyms.

Acronym	Description
V2V	Vehicle-to-vehicle
V2X	Vehicle-to-everything
5G	Fifth generation
6G	Sixth generation
SVD	Singular value decomposition
PCA	Principal component analysis
DRL	Deep reinforcement learning
SNR	Signal-to-noise ratio
SINR	Signal-to-interference-plus-noise ratio
URLLC	Ultra-reliable low-latency communication
eMBB	Enhanced mobile broadband
mMTC	Massive machine-type communication
QoS	Quality of service
DoA	Direction of arrival
MIMO	Multiple-input multiple-output
CSI	Channel state information
AMC	Adaptive modulation and coding
MCS	Modulation and coding scheme

. The structure of the paper contains related work as Section 2. Section 3 discusses the system model, experimental settings are part of Section 4, Section 5 contains results and discussions, and, finally, Section 6 consists of the conclusion.

2. Related Work

Beamforming techniques have been extensively studied in wireless communication systems to improve the signal-to-interference-plus-noise ratio (SINR), increase capacity, and enhance communication reliability [4]. In vehicular communication systems, adaptive beamforming and beam tracking techniques have been proposed to maintain optimal beam alignment in the rapidly changing environment [5]. Various beam tracking algorithms, such as the Kalman filter [6] and particle filter [7], have been used to predict the direction of arrival (DoA) of the received signal and adjust the beamforming weights accordingly. Switched beam antennas have been proposed as a promising solution for adaptive beamforming in V2V communication systems [8], due to their ability to dynamically adjust their radiation patterns. The aforementioned approaches are state-of-the-art, but with the increased growth of automation, the role of ML/AI integrated with the above techniques is considered necessary.

DRL-based approaches have recently gained significant attention in vehicular communication systems due to their ability to learn optimal control policies in complex and dynamic environments [9] and to enhance automation of aforementioned techniques. DRL has been applied to various aspects of vehicular networks, such as path planning [10], platoon formation [11], and cooperative driving [12]. In the context of beamforming, DRL-based approaches have been proposed to optimize communication links in V2V and V2X scenarios [13]. These approaches typically employ deep neural networks (DNNs) to approximate the optimal policy, which is used to make real-time decisions on resource allocation and beamforming [14]. However, current DRL-based technologies leverage the 5G network for V2V use cases, but beyond 5G, certain challenges are observed with the existing technologies.

With the emergence of 6G networks, new techniques and technologies have been proposed to enhance the performance of V2V communication systems [15]. The use of terahertz (THz) frequency bands in 6G networks enables ultrahigh data rates and improved capacity [16]. However, it also introduces new challenges, such as high path loss, molecular absorption loss, and scattering effects. To address these challenges, various THz-specific beamforming and resource allocation schemes have been proposed in the literature [17]. Additionally, the importance of ultra-reliable low-latency communication (URLLC) in 6G networks has led to the development of new resource allocation and beamforming techniques that prioritize latency minimization and reliability enhancement [18].

Hybrid beamforming, which combines digital and analog beamforming, has been proposed as a potential solution to address the hardware constraints and power consumption issues in large-scale antenna systems [8]. Hybrid beamforming techniques can provide a trade-off between performance and complexity, making them suitable for vehicular communication systems, where low latency and energy efficiency are critical requirements [19]. Several hybrid beamforming schemes have been proposed in the literature, considering different antenna architectures and optimization objectives [20]. However, limited analysis of work has been investigated regarding the integration of hybrid beamforming techniques with switched beam antennas in the context of 6G V2V communication systems.

Furthermore, in the realm of 6G channel modeling [21], two broad categories exist: stochastic and deterministic models. The ray-tracing method, a deterministic model, reconstructs the three-dimensional space, including both azimuth and elevation angles, to search for rays, but its high computational complexity makes it suitable only for specific communication scenarios.

Despite the extensive research in the areas of beamforming, and DRL-based approaches in vehicular communication systems, there is a lack of comprehensive studies that integrate these techniques with the unique features of 6G networks and switched beam antennas. Moreover, the majority of current studies are mainly conducted on frequency bands of 5G. The proposed DRL-based adaptive beam tracking and resource allocation framework for 6G V2V communication systems with switched beam antennas aims to fill this gap, providing a robust and high-performance solution for next-generation vehicular communication systems.

3. System Model

We propose a novel mathematical model by incorporating a proposed hierarchical deep reinforcement learning (HDRL) approach to optimize beam selection, adaptive modulation and coding (AMC), and power allocation simultaneously. This high-level model will enhance the system’s performance by considering multiple aspects of the V2V communication. In Figure 1, HDRL is implemented partially on the transmitted and receiver side to observe holistic response analysis of the system model.

3.1. Hierarchical Deep Reinforcement Learning Framework

The HDRL framework consists of two levels of DRL agents: a high-level agent for beam selection and a low-level agent for AMC and power allocation optimization, as shown in Figure 2.

The high-level DRL agent is responsible for selecting the optimal beam among the available beams based on the communication environment state. It employs a deep Q-network (DQN) to approximate the optimal action-value function [22].

$$Q_{High}(s,a)\approx f_{high}(s,{\theta }_{high})$$

(1)

where s is the state of the environment, a is the beam selection action, ${\theta }_{high}$ is the parameters of the DQN, and $f_{high}$ is the function approximator implemented using a deep neural network. The state representation for the low-level DRL agent includes the received signal strength, interference levels, and the estimated CSI for the selected beam.

Similarly, the low-level DRL agent optimizes the modulation and coding scheme (MCS) and power allocation for each V2V communication link based on the selected beam from the high-level DRL agent. This agent also employs a DQN to approximate the optimal action-value function.

$$Q_{Low}(s,a)\approx f_{low}(s,{\theta }_{low})$$

(2)

where s is the state of the communication link, a is the combination of the selected MCS and power allocation, ${\theta }_{low}$ is the parameters of the DQN, and $f_{low}$ is the function approximator implemented using a deep neural network.

The state representation for the low-level DRL agent includes the received signal strength, interference levels, and the estimated CSI for the selected beam.

The system estimates the CSI using a two-step approach: pilot-based estimation and deep learning-based interpolation.

3.1.1. Pilot-Based Estimation

Vehicles periodically transmit pilot symbols over a dedicated resource. The received pilot symbols at each vehicle are used to estimate the CSI between the transmitter and receiver vehicle pairs. The CSI estimation for a given vehicle pair i and j can be given as

$$H_{ij}=Y_{ij}·{\left(X_{ij}\right)}^{-1}$$

(3)

where $H_{ij}$ is the estimated channel matrix, $Y_{ij}$ is the received pilot symbol matrix, and $X_{ij}$ is the transmitted pilot symbol matrix.

3.1.2. Deep-Learning-Based Interpolation

A deep learning model is employed to interpolate the CSI estimates between the pilot symbol transmissions. This model takes the estimated CSI and other relevant state information as input and predicts the interpolated CSI for the V2V communication links.

$$H_{Interpolated}=f_{IN}(H_{Es},s_{IN},{\theta }_{IN})$$

(4)

where Es shows estimated value of H, and IN shows interpolation of specific values.

$H_{Interpolated}$ is the interpolated CSI, $H_{Estimated}$ is the pilot-based CSI estimation, $s_{interpolation}$ is the additional state information used for interpolation, ${\theta }_{interpolation}$ is the deep learning model’s parameters, and $f_{interpolation}$ is the function approximator implemented using a deep neural network.

The reward function $R_{High}(s,a)$ for the high-level DRL agent is designed to encourage selecting the optimal beam that maximizes the received signal strength and minimizes interference with other ongoing V2V communication links. The reward function is based on the following components:

• Received signal strength for the selected beam;
• Interference levels for the selected beam.

The beam-switching cost term shown in upcoming equation, denoted by “BeamSwitchingCost(a)” and weighted by $\gamma$, in the reward function $R_{High}(s,a)$ of the deep reinforcement learning (DRL) model for switched beam antenna systems is crucial for achieving a balance between communication quality and energy efficiency. By incorporating this term alongside received signal strength indicator (RSSI) and interference, the DRL model can make informed beam selection decisions that account for the energy and time costs associated with changing beams. The choice of $\gamma$ directly impacts the model’s behavior, with higher values emphasizing energy efficiency and lower values prioritizing signal strength and interference reduction. This comprehensive approach enables the DRL model to optimize the performance of the switched beam antenna system in 6G V2V communication scenarios.

$$\begin{array}{cc}\hfill R_{High}(s,a)& =\alpha ·RSSI(s,a)\hfill \\ \hfill & -\beta ·Interference(s,a)\hfill \\ \hfill & -\gamma ·BeamSwitchingCost\left(a\right)\hfill \end{array}$$

(5)

where $\alpha$, $\beta$, and $\gamma$ are the weights assigned to the components of the reward function, RSSI(s, a) is the received signal strength indicator for the selected beam, Interference(s, a) is the interference level for the selected beam, and BeamSwitchingCost(a) represents the cost of switching between beams.

The reward function $R_{Low}(s,a)$ for the low-level DRL agent aims to encourage the selection of an optimal MCS and power allocation that maximize the communication link’s spectral efficiency while maintaining a target bit error rate (BER) and minimizing power consumption. The reward function is based on the following components:

• Spectral efficiency for the selected MCS and power allocation;
• Bit error rate for the selected MCS and power allocation;
• Power consumption for the selected power allocation.

$$\begin{array}{cc}\hfill R_{Low}(s,a)& =\delta ·SpectralEfficiency(s,a)\hfill \\ \hfill & -ϵ·BER(s,a)\hfill \\ \hfill & -\zeta ·PowerConsumption\left(a\right)\hfill \end{array}$$

(6)

where $ϵ$, $\delta$, and $\zeta$ are the weights assigned to the components of the reward function, SpectralEfficiency(s, a) is the spectral efficiency for the selected MCS and power allocation, BER(s, a) is the bit error rate for the selected MCS and power allocation, and PowerConsumption(a) represents the power consumption for the selected power allocation.

3.2. Proposed Switched Beam Antenna Design with Hierarchical Deep Reinforcement Learning

In the proposed antenna system model for the 6G V2V communication system, patch antennas are chosen as the array elements. Patch antennas are more suitable for this model due to their compact size, low profile, and compatibility with higher frequency operation, such as terahertz frequency bands. These characteristics make patch antennas an ideal choice for integrating into vehicles and providing the desired gain, bandwidth, and radiation patterns necessary for efficient and reliable V2V communication in a 6G network. The proposed switched beam antenna design consists of an M × N-element planar array with a rectangular lattice structure, where M and N represent the number of elements along the x and y axes, respectively. The spacing between adjacent elements along the x-axis is denoted as dx, and along the y-axis is dy. The array factor for the M × N-element planar array can be given as follows:

$$AF(\theta ,\phi )=\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}{W}_{mn}{e}^{jk(m{d}_{x}sin\theta cos\phi +n{d}_{y}sin\theta sin\phi )}$$

(7)

where $\theta$ and $\phi$ are the elevation and azimuth angles of the signal arrival, respectively, $W_{mn}$ is the weight applied to the $mn$-th antenna element, k is the wavenumber $(2\pi /\lambda )$, and m and n are the element indices along the x and y axes, respectively.

The beamforming network (BFN) is responsible for applying the appropriate weights to the antenna elements to form multiple reconfigurable beams with different main lobe directions and beamwidths. The BFN can be implemented using a combination of phase shifters, tunable attenuators, and Butler matrices. The weights $W_{mn}$ can be given as

$$W_{mn}=A_{mn}·exp(j·{\varphi }_{mn})$$

(8)

where $T_n\left(C\right)$ and $T_m\left(C\right)$ are the Chebyshev polynomials of order n and m, respectively, and C is the sidelobe level parameter.

For the Taylor synthesis, the weights can be determined by

$$W_{mn}=F_n(L,\sigma )·F_m(L,\sigma )$$

(9)

where $F_n(L,\sigma )$ and $F_m(L,\sigma )$ are the Taylor weight functions of order n and m, respectively, L is the number of array elements considered in the main beam, and $\sigma$ is the sidelobe level parameter.

The high-level DRL agent, responsible for selecting the optimal beam, incorporates the complex switched beam antenna design into its state representation and action space. The state representation for the high-level DRL agent is extended to include additional information related to the complex switched beam antenna design, such as:

• Current beam configuration (main lobe direction and beamwidth);
• Estimated CSI for each beam in the antenna’s set of beams.

The action space for the high-level DRL agent is expanded to accommodate the complex switched beam antenna design. The agent can now select actions corresponding to different beam configurations (main lobe directions and beamwidths) in the antenna’s set of beams. The expanded action space allows the DRL agent to adaptively configure the switched beam antenna to maximize the received signal strength and minimize interference.

3.3. Beam Selection and MCP Adaptation

In the proposed 6G V2V communication system model with a switched beam antenna and deep reinforcement learning, the beams and modulation and coding pairs (MCPs) are selected to optimize the overall system performance. The high-level DRL agent is responsible for beam selection, while the low-level DRL agent is responsible for the adaptation of the MCPs. The high-level DRL agent selects beams from a predefined set of beam patterns, which includes omnidirectional, sector, and adaptive beams. The omnidirectional beam provides equal gain in all directions, while sector beams are divided into multiple narrower beams, each covering a specific angular range (e.g., 30°, 60°, or 90° sectors). Adaptive beams are formed using digital beamforming techniques to provide better directionality and gain.

The high-level DRL agent learns to select the optimal beam pattern based on the current channel conditions, vehicular mobility, and system requirements. The objective of the high-level DRL agent is to maximize the signal-to-interference-plus-noise ratio (SINR) and improve the overall system capacity.

The low-level DRL agent adapts the modulation and coding pairs (MCPs) based on the current channel quality, interference levels, and system requirements, such as latency and reliability constraints. The MCPs used in the system include QPSK, 16-QAM, and 64-QAM modulation schemes, paired with various error-correcting codes, such as convolutional codes, turbo codes, or LDPC (low-density parity-check) codes.

The low-level DRL agent learns to adapt the MCPs by balancing between maximizing the data rate and minimizing the bit error rate (BER) under varying channel conditions. The objective of the low-level DRL agent is to achieve the highest possible throughput while maintaining the desired level of reliability and latency in the V2V communication system.

The proposed 6G V2V communication system model utilizes deep reinforcement learning to adaptively select beams and MCPs based on the current channel conditions and system requirements. The high-level DRL agent is responsible for beam selection, while the low-level DRL agent adapts the MCPs, resulting in optimized system performance under various V2V communication scenarios.

In situations where the bit error rate (BER) is very high and the channel state information (CSI) is hostile, the proposed deep reinforcement learning (DRL)-based 6G V2V communication system model effectively adapts its beam selection and modulation and coding pairs (MCPs) to maintain the desired level of communication reliability and performance.

In the presence of high BER and hostile CSI, the high-level DRL agent responsible for beam selection focuses on choosing beams with higher directionality and gain. This involves selecting adaptive beams formed using digital beamforming techniques, which concentrate the transmitted power precisely towards the intended receiver, reducing the impact of interference and noise. The high-level DRL agent continuously learns and adapts its beam selection strategy based on the current channel conditions to improve the signal-to-interference-plus-noise ratio (SINR) and overall system capacity.

Similarly, the low-level DRL agent responsible for MCP adaptation responds to the high BER and hostile CSI by selecting more robust modulation schemes and error-correcting codes. For instance, it chooses lower-order modulation schemes such as QPSK, which are more resilient to noise and interference compared to higher-order schemes such as 16-QAM or 64-QAM. Additionally, the low-level DRL agent opts for more powerful error-correcting codes, such as turbo codes or LDPC codes, which can effectively recover the transmitted data despite a high level of errors in the received signal.

By adaptively selecting beams and MCPs in response to high BER and hostile CSI, the proposed DRL-based 6G V2V communication system model maintains reliable communication links and ensures that the desired level of performance is achieved even under challenging communication scenarios. This adaptive approach allows the system to dynamically balance the trade-offs between data rate, reliability, and latency in real time, providing robust and efficient V2V communication.

3.4. Mathematical Model of Beam Tracking Ability for Switched Beam Antenna

The beam tracking model aims to maintain the optimal beam alignment between the transmitter and receiver in a V2V communication system by continuously updating the switched beam antenna configuration, as shown in Figure 3. The beam tracking model is formulated as a discrete-time control problem, with the objective of minimizing the misalignment between the desired and actual beam directions while considering the dynamics of the vehicular environment.

The state representation for beam tracking includes the following variables:

• Relative angle ${\theta }_k\left(t\right)$: The relative angle between the desired and actual beam directions for the k-th V2V link at time t.
• Angular velocity ${\omega }_k\left(t\right)$: The angular velocity of the k-th V2V link at time t.
• Angular acceleration ${\alpha }_k\left(t\right)$: The angular acceleration of the k-th V2V link at time t.

The state vector for beam tracking can be represented as:

$$s_k\left(t\right)=[{\theta }_k\left(t\right),{\omega }_k\left(t\right),{\alpha }_k\left(t\right)]$$

(10)

The control input for beam tracking is the action selected by the high-level DRL agent, which corresponds to the beam configuration of the switched beam antenna for the k-th V2V link:

$$u_k\left(t\right)=a_{hig{h}_k}\left(t\right)$$

(11)

The dynamics of the beam tracking model can be represented as a set of difference equations, which describe the evolution of the state variables over time:

$${\theta }_k(t+1)={\theta }_k\left(t\right)+{\omega }_k\left(t\right)\Delta t+\frac{1}{2}{\alpha }_k\left(t\right){(\Delta t)}^2$$

(12)

$${\omega }_k(t+1)={\omega }_k\left(t\right)+{\alpha }_k\left(t\right)\Delta t$$

(13)

where $\Delta t$ is the time step duration.

The beam tracking cost function is designed to minimize the misalignment between the desired and actual beam directions, as well as the control effort required to update the beam configuration. The cost function can be represented as:

$$C_k\left(t\right)={\gamma }_1·|{\theta }_k(t+1)-{\theta }_k\left(t\right)|+{\gamma }_2·|u_k(t+1)-u_k\left(t\right)|$$

(14)

where ${\gamma }_1$ and ${\gamma }_2$ are the weights assigned to the misalignment and control effort components, respectively.

The objective of the beam tracking model is to minimize the total cost over a finite time horizon T:

$$\begin{array}{cc}\hfill & min\sum _{t=0}^{T-1}{C}_k\left(t\right)\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & C_k\left(t\right)={\gamma }_1\ast |{\theta }_k(t+1)-{\theta }_k\left(t\right)|+{\gamma }_2\ast |u_k(t+1)-u_k\left(t\right)|\hfill \\ \hfill & {\theta }_k(t+1)={\theta }_k\left(t\right)+{\omega }_k\left(t\right)\Delta t+0.5{\alpha }_k\left(t\right){(\Delta t)}^2\hfill \\ \hfill & {\omega }_k(t+1)={\omega }_k\left(t\right)+{\alpha }_k\left(t\right)\Delta t\hfill \end{array}$$

(15)

subject to the beam tracking dynamics and the constraints on the state variables and control inputs. After substitution of $C_k\left(t\right)$ into the objective function, we obtained

$$\begin{array}{cc}\hfill & min\sum _{t=0}^{T-1}\left[{\gamma }_1\ast |{\theta }_k(t+1)-{\theta }_k\left(t\right)|\right.\hfill \\ \hfill & \left.+{\gamma }_2\ast |u_k(t+1)-u_k\left(t\right)|\right]\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\hfill \\ \hfill & {\theta }_k(t+1)={\theta }_k\left(t\right)+{\omega }_k\left(t\right)\Delta t\hfill \\ \hfill & +0.5{\alpha }_k\left(t\right){(\Delta t)}^2\hfill \\ \hfill & {\omega }_k(t+1)={\omega }_k\left(t\right)+{\alpha }_k\left(t\right)\Delta t\hfill \end{array}$$

(16)

The given equation represents the optimization problem for a beam tracking model in a V2V communication system with switched beam antennas. The objective is to minimize the total cost over a finite time horizon T, where the cost consists of two components: the misalignment between the desired and actual beam directions, and the control effort required to update the beam configuration. The weights ${\omega }_1$ and ${\omega }_2$ are used to balance the importance of these components in the cost function.

The optimization problem is subject to the dynamics of the beam tracking model, described by the difference equations for the relative angle (${\theta }_k$) and angular velocity ${\omega }_k\left(t\right)$ of the k-th V2V link. The dynamics take into account the angular acceleration ${\alpha }_k\left(t\right)$ and time step duration $\Delta t$ to capture the evolution of the state variables over time. By solving this optimization problem, the optimal beam configuration can be determined to minimize the misalignment and control effort, thereby improving the performance of the V2V communication system.

3.5. Multiobjective Optimization with Pareto-Based Hierarchical Deep Reinforcement Learning

The proposed work incorporates multiobjective optimization using a Pareto-based hierarchical deep reinforcement learning (PHDRL) approach. The PHDRL framework considers multiple objectives, including maximizing the system throughput, minimizing latency, and minimizing power consumption, to optimize the proposed switched beam antenna system.

The Pareto-based reward function combines the objectives of the high-level and low-level DRL agents to encourage a trade-off between the multiple objectives in a balanced manner. The Pareto-based reward function can be given as:

$$\begin{array}{cc}\hfill R_{Pareto}(s,a)& ={\lambda }_1·R_{High}(s_{high},a_{high})\hfill \\ \hfill & +{\lambda }_2·R_{Low}(s_{low},a_{low})\hfill \\ \hfill & +{\lambda }_3·R_{Latency}(s,a)\hfill \end{array}$$

(17)

where ${\lambda }_1$, ${\lambda }_2$, and ${\lambda }_3$ are the weights assigned to the high-level agent’s reward, low-level agent’s reward, and latency-based reward, respectively.

The latency-based reward, $R_{Latency}(s,a)$, is designed to encourage minimizing the end-to-end latency in the V2V communication system. It can be given as:

$$R_{Latency}(s,a)=-\xi ·Latency(s,a)$$

(18)

where $-\xi$ is the weight assigned to the latency component, and Latency(s, a) represents the end-to-end latency for the selected beam, AMC, and power allocation.

The PHDRL framework employs a Pareto-based action selection strategy, which selects actions that provide the best trade-off between the multiple objectives. The Pareto-based action selection is given as:

$$a_{Pareto}=argmaxa{Q}_{Pareto}(s,a)$$

(19)

where $Q_{Pareto}(s,a)$ is the Pareto-based action-value function, which can be approximated using a deep Q-network (DQN) as follows:

$$Q_{Pareto}(s,a)\approx f_{Pareto}(s,{\theta }_{Pareto})$$

(20)

where ${\theta }_{Pareto}$ is the parameters of the DQN, and $f_{Pareto}$ is the function approximator implemented using a deep neural network.

3.6. Computational Model for Proposed System Model

To reduce the computational complexity of the above-explained Pareto-based hierarchical deep reinforcement learning system, we propose a matrix-based computational model that exploits the inherent structure of the problem. This model leverages matrix operations and low-rank approximations to reduce computational complexity while preserving the performance of the system.

We represent the states and actions for the high-level and low-level DRL agents as matrices.

The state matrix S is an L × K matrix, where L is the number of state variables and K is the number of V2V links:

$$S=[s_1,s_2,\dots ,s_K]$$

(21)

Each column $a_k$ in A represents the action for the k-th V2V link, which includes the selected beam configuration, AMC, and power allocation for both the high-level and low-level agents.

The Pareto-based reward function can be represented as a matrix R, which is an M × K matrix:

$$R={\lambda }_1·R_{High}+{\lambda }_2·R_{Low}+{\lambda }_3·R_{Latency}$$

(22)

where $R_{High},R_{Low},\mathrm{and}{R}_{Latency}$ are M × K matrices representing the high-level agent’s reward, low-level agent’s reward, and latency-based reward, respectively, for all possible actions and V2V links.

Singular value decomposition (SVD) is employed as a low-rank approximation technique for reducing the dimensions and computational complexity of state and action matrices. SVD offers inherent advantages over principal component analysis (PCA), making it the preferred choice when dealing with data with unknown or noncentered properties. This attribute is especially significant in the context of a complex 6G V2V system model that encompasses large and diverse datasets. SVD also exhibits superior numerical stability and performance when processing extensive and intricate datasets compared to PCA. This robustness plays a crucial role in ensuring the accurate and efficient handling of the vast amount of data generated by the 6G V2V system model. As a result, SVD proves to be the ideal method for addressing the system’s complexity and computational requirements.

$$S\approx S_r=U_r·{\mathrm{\Sigma }}_r·V_r^T$$

(23)

$$A\approx A_r=U_a·{\mathrm{\Sigma }}_a·V_a^T$$

(24)

where $S_r$ and $A_r$ are the low-rank approximations of the state and action matrices, respectively, and $U_r$, ${\mathrm{\Sigma }}_r$, $V_r$, $U_a$, ${\mathrm{\Sigma }}_a$, and $V_a$ are the corresponding factors obtained from the SVD.

The Pareto-based action selection can be performed using the low-rank approximations of the state and action matrices:

$$a_{Pareto}=argmaxa{Q}_{Pareto}(S_r,A_r)$$

(25)

where $Q_{Pareto}(S_r,A_r)$ is the matrix-based Pareto action-value function, which can be approximated using a matrix factorization technique, such as non-negative matrix factorization (NMF) or matrix completion:

$$Q_{Pareto}(S_r,A_r)\approx W·H$$

(26)

where W and H are non-negative matrices obtained from the NMF or matrix completion technique.

To make the computational model more mathematically sophisticated, we incorporate efficient matrix operations and large-scale matrix solvers. This will enhance the model’s scalability and robustness, enabling it to handle large-scale V2V communication networks with complex switched beam antennas.

Matrix operations, such as multiplication, addition, and inversion, are essential in the proposed computational model. To improve the efficiency of these operations, we can utilize optimized linear algebra libraries, such as BLAS, LAPACK, or cuBLAS, which are designed for high-performance computing on CPUs and GPUs.

In the proposed computational model, the state and action matrices can become large as the number of V2V links increases. To handle large-scale matrices, we can employ parallel and distributed matrix solvers, such as the conjugate gradient (CG) method or the preconditioned conjugate gradient (PCG) method. These solvers can effectively reduce the computational complexity and memory requirements for large-scale matrix problems.

For the matrix-based action selection, we can use large-scale matrix solvers to compute the Pareto action-value function.

$Q_{Pareto}(S_r,A_r)$ can be solved using large-scale matrix solvers, such as the CG or PCG methods, to efficiently compute the optimal actions for all V2V links.

Mathematical formulation for the computational model, incorporating efficient matrix operations and large-scale matrix solvers, can be summarized as follows:

• Represent the states and actions as matrices S and A, respectively;
• Apply low-rank approximation techniques, such as SVD or PCA, to reduce the dimensions of the state and action matrices;
• Compute the matrix-based Pareto reward function;
• Employ large-scale matrix solvers to compute the matrix-based Pareto action-value function for all V2V links;
• Select the optimal actions based on the computed Pareto action-value function.

By incorporating efficient matrix operations and large-scale matrix solvers, the computational model becomes more mathematically sound and scalable, enabling it to handle large-scale V2V communication networks with complex switched beam antennas.

3.7. Terahertz Communication for V2V

To provide a mathematical analysis of the role of proposed switched beam antennas in 6G V2V communications, we will focus on the signal-to-interference-plus-noise ratio (SINR) as a performance metric, which is crucial in determining the overall communication performance.

The SINR for a V2V communication link at time t can be expressed as:

$$\mathrm{SIN}\mathrm{R}\left(t\right)=\frac{P_{signal}\left(t\right)}{P_{interference}\left(t\right)+P_{noise}\left(t\right)}$$

(27)

where $P_t$ is the transmitted power, $G_t\left(t\right)$ and $G_r\left(t\right)$ are the transmitter and receiver antenna gains at time t, respectively, and $L_{channel}\left(t\right)$ is the channel path loss at time t.

The switched beam antenna contributes to enhancing the SINR by improving the received signal power and reducing the interference power. The received signal power can be expressed as:

$$P_{signal}\left(t\right)=P_t·G_t\left(t\right)·G_r\left(t\right)·L_{channel}\left(t\right)$$

(28)

where $P_t$ is the transmitted power, $G_t\left(t\right)$ and $G_r\left(t\right)$ are the transmitter and receiver antenna gains at time t, respectively, and $L_{channel}\left(t\right)$ is the channel path loss at time t. The interference power can be expressed as:

$$P_{interference}\left(t\right)=\sum _i(P_{t_i}·G_{t_i}\left(t\right)·G_{r_i}\left(t\right)·L_{{channel}_i}\left(t\right))$$

(29)

where the summation is over all interfering V2V links, $P_{ti}$ is the transmitted power of the interfering link i, $G_{ti}\left(t\right)$ and $G_{ri}\left(t\right)$ are the transmitter and receiver antenna gains for the interfering link i at time t, and $L_{channeli}\left(t\right)$ is the channel path loss for the interfering link i at time t.

By employing switched beam antennas, the antenna gains $G_t\left(t\right)$ and $G_r\left(t\right)$ can be optimized to maximize the received signal power and minimize the interference power. The optimal antenna configuration can be determined using the DRL-based beam tracking and resource allocation model.

The problem of maximizing the SINR for a V2V communication link using switched beam antennas can be formulated as an optimization problem:

$$max\mathrm{SIN}\mathrm{R}\left(t\right)=\frac{P_{signal}\left(t\right)}{P_{interference}\left(t\right)+P_{noise}\left(t\right)}$$

(30)

subject to the antenna configurations and channel conditions at time t.

To provide a more advanced numerical analysis, we used stochastic geometry to model the spatial distribution of vehicles and their communication links. The Poisson point process (PPP) can be employed to describe the locations of vehicles in the V2V network. Let $\mathsf{\Phi }$ be a homogeneous PPP with density $\lambda$ representing the vehicle locations in a two-dimensional plane.

The probability density function (pdf) of the distance between a transmitter–receiver pair can be given as:

$$f_R\left(r\right)=2\pi \lambda rexp(-\pi \lambda r^2)$$

(31)

Using stochastic geometry, we can derive the SINR distribution for the V2V communication link. The complementary cumulative distribution function (CCDF) of the SINR can be expressed as:

$$P(\mathrm{SIN}\mathrm{R}\left(t\right)>\gamma )=exp\left(-\pi \lambda {\int }_0^{\infty }(1-P_{succ}(r,\gamma ))r,dr\right)$$

(32)

where $\gamma$ is the SINR threshold, and $P_{succ}(r,\gamma )$ is the success probability of the V2V link as a function of the distance r and SINR threshold $\gamma$.

By analyzing the SINR distribution using advanced mathematics such as stochastic geometry, we can gain insights into the performance of the switched beam antenna in 6G V2V.

3.8. Holistic Contrast with Shanon’s Theorem

Shannon’s theorem, or the Shannon–Hartley theorem, states that the maximum achievable data rate for a given channel under the assumption of additive white Gaussian noise (AWGN) and the use of ideal error-correcting codes is:

$$C=B{log}_2\left(1+\frac{S}{N}\right)$$

(33)

where C is the channel capacity in bits per second (bps), B is the bandwidth of the channel in hertz (Hz), S is the signal power, and N is the noise power. The proposed DRL-based system aims to optimize beam selection and modulation and coding pairs (MCPs) in a complex and dynamic V2V communication environment. Although it is difficult to derive strict bounds on the system’s performance, the adaptive nature of the DRL agents enables the system to approach the theoretical limits under various conditions.

Assuming that the DRL agents can achieve near-optimal performance in selecting beams and MCPs, the performance of the proposed system can be expressed as a fraction of the Shannon capacity:

$$R=\eta C$$

(34)

where R is the achievable data rate for the proposed DRL-based system, and $\eta$ is the efficiency factor, representing the fraction of the Shannon capacity that can be achieved by the DRL-based system. The efficiency factor $\eta$ depends on the effectiveness of the DRL agents in learning and adapting to the environment. It is expected to be less than 1 due to the uncertainties and complexities involved in a real-world V2V communication scenario. However, as the DRL agents continuously learn and adapt to the environment, the efficiency factor $\eta$ can be expected to increase, approaching the performance limits set by Shannon’s theorem.

While providing exact estimations of the upper and lower bounds on the performance of the proposed DRL-based 6G V2V communication system model in contrast to Shannon’s theorem is challenging, the system aims to approach these theoretical limits by dynamically optimizing beam selection and MCPs in response to the changing communication environment.

3.9. Computational Complexity of System Model

The proposed 6G V2V communication system utilizing HRDL is designed to address computational efficiency and real-time performance, considering the time-consuming processes involved, such as CSI estimation, DRL, and radio resource allocation. The system employs singular value decomposition (SVD) for dimensionality reduction, which enhances numerical stability and performance while handling large and complex datasets, thus reducing the computational burden.

The HRDL model separates tasks into high-level and low-level DRL agents, allowing for parallel processing and reducing overall complexity. The high-level agent selects the optimal beam and modulation and coding scheme (MCS), while the low-level agent focuses on beam alignment and power control. This hierarchical structure enables efficient resource management and reduces the computation time required for decision making.

Moreover, advanced algorithms and techniques are used for CSI estimation and resource allocation, further reducing the computational load. For instance, the system utilizes efficient algorithms for AoA and AoD estimation, which are essential for accurate CSI estimation. Furthermore, the DRL model employs exploration–exploitation trade-off strategies, such as $ϵ$-greedy or upper confidence bound (UCB) algorithms, which accelerate convergence while optimizing the overall system performance.

To ensure real-time performance, the system is designed to work with modern hardware accelerators and parallel processing architectures, such as GPUs or specialized AI processors. These hardware components can significantly speed up the calculations and enable real-time operation in dynamic vehicular environments.

Overall, the proposed 6G V2V communication system with HRDL effectively addresses computational complexity and real-time performance by leveraging advanced algorithms, techniques, and hardware accelerators. The hierarchical structure, dimensionality reduction, parallel processing, and optimized resource allocation contribute to making the system suitable for real-time vehicular networks.

4. System Implementation

To implement the proposed mathematical models using software-based simulation, we followed the following steps:

• For the communication system simulation, we used combination MATLAB. To implement the DRL-based algorithms, we used deep learning PyTorch as the main base framework.
• We developed a realistic channel model and simulation environment that captures the unique features of 6G V2V communication systems, such as terahertz communication, ultra-reliable low-latency communication, and dynamic vehicular mobility. This channel model should be integrated into the selected communication system simulator.
• We implemented the switched beam antenna-based MIMO system model using MATLAB’s Antenna Toolbox. We defined the radiation patterns, antenna array geometry, and beam-switching mechanisms and ensured the antenna parameters were consistent with the operating frequency range of 6G systems.
• We developed a channel model specific to 6G V2V communication, incorporating path loss, molecular absorption, scattering, and multipath fading. We considered the impact of vehicular mobility on the channel dynamics, such as the Doppler effect and time-varying channel coefficients. We used MATLAB’s Communication Toolbox to implement the channel model.
• We implemented the physical (PHY) and medium access control (MAC) layers of the 6G V2V communication system using MATLAB and Simulink and included the necessary modulation schemes, coding techniques, and resource allocation methods suitable for 6G networks.
• We implemented the DRL-based beam tracking and resource allocation model using MATLAB’s Reinforcement Learning Toolbox with integration of PyTorch framework for interpolation deep neural agents. We designed the neural network architecture for the DRL model, including multiple hidden layers, convolutional layers, and activation functions. We implemented the state space, action space, and reward function considering the unique features of 6G V2V communication systems.

A list of simulation parameters is depicted in

Table 2. Simulation parameters and environmental factors.

Parameter	Value
Number of beams	8
Beam patterns	Uniform linear array (ULA)
SNR levels	−10 to 30 dB
Channel model	Tapped delay line (TDL)
Channel assumption	Time-varying Rayleigh fading
Phase distribution	Uniform
Amplitude distribution	Rayleigh
Modulation schemes	QPSK, 16-QAM, 64-QAM, 256-QAM
Coding rates	1/2, 2/3, 3/4, 5/6
MCPs	Combination of modulation schemes and coding rates
Bandwidth	20 MHz
Carrier frequency	28 GHz
Antenna elements	64

. The performance outcomes may exhibit discrepancies not only between simulation-based evaluations and real-world implementations due to variations in equipment characteristics and the surrounding environmental conditions in the deployed scenario, but also among different simulation runs, as the underlying assumptions and parameters can lead to divergent outcomes.

4.1. Deep Reinforcement Learning Model Architecture and Design Choices

In the proposed system model, we carefully selected the model architecture and its components to ensure optimal performance and efficient learning. An explanation of the architectural choices is as follows:

• Hidden layers: We used three hidden layers in the proposed deep reinforcement learning model. This decision was made after a thorough analysis, which indicated that three layers provided a good trade-off between model complexity and performance. With too few layers, the model may not capture the intricacies of the problem, while too many layers might lead to overfitting and increased computational complexity.
• Epoch size: The model was trained for 100 epochs. This number was selected after monitoring the validation loss during training. It was observed that after 100 epochs, the validation loss had converged, and further training did not provide significant improvements in performance. Training for more epochs could potentially lead to overfitting, while fewer epochs might result in an undertrained model.
• Architecture: The problem at hand does not involve image processing tasks; therefore, we did not incorporate convolutional or deconvolutional layers in the proposed model. Instead, we employed fully connected layers, also known as dense layers, to model the relationships between input features. This choice ensures that the model can learn complex patterns and dependencies in the input data, which is crucial for optimizing the antenna design and 6G V2V communication.
• Activation functions: We chose the rectified linear unit (ReLU) activation function for all hidden layers due to its ability to mitigate the vanishing gradient problem and speed up training. ReLU is a widely used activation function in deep learning models, as it introduces nonlinearity into the model without increasing computational complexity. For the output layer, we used a linear activation function because reinforcement learning problem involves a continuous action space. The linear activation function allows the model to output a range of continuous values, ensuring a smooth mapping between the input state and the action space.

4.2. Dataset

Deep reinforcement learning (DRL) models typically do not rely on pre-existing datasets, as they learn from interactions with the environment during the training process. However, we generated a synthetic dataset that simulates the V2V communication environment to train and validate the DRL model. The dataset includes channel state information (CSI), vehicular positions and mobility patterns, network load and traffic demand, beam alignment, and resource allocation decisions.

To generate a synthetic dataset we initally simulated various network scenarios with different vehicular densities, speeds, and channel conditions using the developed simulation environment. Then, we recorded the state variables (such as channel coefficients, signal-to-noise ratio, and beam-alignment error) and the corresponding optimal actions (beamforming weights, beam selection, and resource allocation) for each scenario. Furthermore, we split the dataset into 70% of training and 30% of testing subsets, ensuring that each subset had a diverse range of scenarios to avoid overfitting and to ensure generalization.

4.3. Detailed Integration Process

This step involves ensuring that the different models, including the switched beam antenna-based MIMO system, hybrid beamforming, DRL-based beam tracking, and resource allocation models, are synchronized within the V2V communication environment. This involves aligning the time scales, updating rates, and interaction mechanisms among the models. We used MATLAB and Simulink to manage the synchronization and interaction of the models effectively.

After that, we incorporated the channel model, which accounts for the unique features of 6G V2V communication, into the switched beam antenna-based MIMO system. This allows the antenna system to account for the channel conditions when adjusting the beamforming weights and selecting the appropriate beams. To integrate the DRL model with the V2V communication environment, we established an interface that enables the exchange of information between the DRL agent and the environment. This included:

• Transmitting the state variables from the environment to the DRL agent.
• Receiving the action selected by the DRL agent and applying it in the environment.
• Providing the DRL agent with the reward and next state after applying the selected action.

We ensured that the DRL agent can interact with the V2V communication environment in real time and we adapted its control policy based on the dynamic channel conditions and vehicular mobility. This required:

• Efficient implementation of the DRL model, minimizing the computational overhead during the learning process.
• Implementing the DRL model in a distributed manner across the edge computing devices in the V2V communication system, enabling real-time adaptation and decision making.

Proposed DRL training algorithm: This algorithm is responsible for training the deep reinforcement learning (DRL) model for the switched beam antenna system as shown in Algorithm 1. The algorithm initializes the DRL model, including the neural networks that represent the policy and the value functions. It iterates through multiple episodes to collect data, interacting with the environment using the current policy. After each episode, the collected data are used to update the policy and value functions. The algorithm terminates when the maximum number of episodes is reached or the performance converges.

6G Channel modeling and switched beam antenna integration: The integration algorithm for the 6G channel model and the switched beam antenna system aims to analyze the performance of a switched beam antenna in a 6G V2V communication scenario using deep reinforcement learning (DRL). The algorithm starts by initializing both the 6G V2V channel model and the switched beam antenna system, including the initial positions of vehicles, antennas, and other environmental parameters. During each time step of the simulation, the algorithm updates the positions and velocities of the vehicles according to their mobility models and calculates the path loss, shadowing, and multipath fading effects for each V2V link using the 6G channel model as demonstrated in Algorithm 2. This information is used to update the channel state information (CSI). With the updated CSI, the algorithm employs the DRL model to select the best beam direction for each V2V link and adjusts the switched beam antenna system state accordingly. Lastly, the algorithm calculates the resulting signal-to-interference-plus-noise ratio (SINR) for each V2V link, as well as other performance metrics such as throughput, latency, and reliability. This integrated approach provides a comprehensive understanding of the switched beam antenna system’s performance in a 6G V2V communication scenario using deep reinforcement learning.

Algorithm 1 DRL-based switched beam antenna algorithm for 6G V2V communications.

1: Initialize simulation environment 2: Set up experimental scenarios 3: for each scenario do 4:     Initialize DRL agent 5:     for each time step do 6:         Observe current state from the environment 7:         Select action based on DRL agent’s policy 8:         Apply selected action to the environment 9:         Receive reward and next state from the environment 10:         Update DRL agent’s policy 11:         Balance exploration and exploitation 12:     end for 13:     Monitor performance metrics 14: end for 15: Analyze and compare performance of the proposed system model

Algorithm 2 6G channel model and switched beam antenna integration.

1: Initialize 6G channel model parameters 2: Integrate channel model with switched beam antenna-based MIMO system 3: for each time step do 4:     Update vehicular positions and velocities 5:     Generate channel coefficients for each beam based on antenna radiation patterns 6:     Update channel coefficients considering path loss, fading, and mobility 7: end for

DRL-based beam tracking and resource allocation integral algorithm: The integration of the 6G channel model and the switched beam antenna system involves a multistep process which is depicted in Algorithm 3. The algorithm begins by initializing both the 6G V2V channel model and the switched beam antenna system, setting up the initial positions of vehicles, antennas, and other environmental parameters. As the algorithm progresses through each time step, it updates the positions and velocities of the vehicles based on their mobility models, and calculates the path loss, shadowing, and multipath fading effects for each V2V link using the 6G channel model. After updating the channel state information (CSI), the algorithm utilizes the DRL model to select the best beam direction for each V2V link, considering the updated CSI, and adjusts the switched beam antenna system state accordingly. Finally, the algorithm calculates the resulting signal-to-interference-plus-noise ratio (SINR) for each V2V link, as well as other performance metrics such as throughput, latency, and reliability. This integrated approach enables a comprehensive analysis of the switched beam antenna system performance in a 6G V2V communication scenario using deep reinforcement learning.

Algorithm 3 DRL-based beam tracking and resource allocation integration.

1: Initialize DRL agent with random or pretrained weights 2: for each time step do 3:     Observe current state from environment 4:     Select action based on DRL agent’s policy 5:     Update beamforming weights and resource allocation based on action 6:     Transmit data using updated weights and resource allocation 7:     Receive feedback from the environment (reward and next state) 8:     Update DRL agent’s policy using state, action, reward, and next state 9:     Balance exploration and exploitation during learning process 10: end for

Real-time adaptation and learning in 6G: The real-time adaptation and learning algorithm in 6G V2V communication systems focuses on leveraging deep reinforcement learning (DRL) to enable real-time adaptation and learning in dynamic vehicular environments. Algorithm 4 starts by initializing the 6G V2V communication system, including the positions of vehicles, antennas, and other environmental parameters. Throughout the simulation, the positions and velocities of the vehicles are continuously updated according to their mobility models, and the channel state information (CSI) is computed using the 6G channel model, which accounts for path loss, shadowing, and multipath fading effects.

Algorithm 4 Real-time adaptation and learning in 6G V2V communication systems.

1: Initialize and deploy DRL models across edge computing devices 2: Synchronize time scales, updating rates, and interaction mechanisms among models 3: for each time step do 4:     Collect and process local observations from environment 5:     Communicate and exchange local information with neighboring devices 6:     Update global model based on local observations and received information 7:     Adapt to dynamic channel conditions and vehicular mobility in real-time 8: end for 9: Evaluate performance metrics and refine the DRL model based on feedback

With the updated CSI, the DRL model learns to make decisions regarding various aspects of the communication system, such as beamforming, resource allocation, and interference management, to optimize performance metrics such as throughput, latency, and reliability. The DRL model continuously updates its knowledge based on the feedback received from the system, enabling real-time adaptation to the changing communication environment.

As the algorithm progresses, it ensures that the communication system remains robust and efficient in the face of dynamic vehicular scenarios, unpredictable channel conditions, and varying network demands. This real-time adaptation and learning approach, facilitated by deep reinforcement learning, plays a crucial role in improving the overall performance and reliability of 6G V2V communication systems.

Training parameters and training time for the proposed DRL model are depicted in

Table 3. DRL model training parameters and time.

Parameter	Value
Number of layers	3
Number of neurons per layer	128
Activation function	ReLU
Learning rate	0.0001
Batch size	32
Optimizer	Adam
Loss function	Huber Loss
Number of episodes	1000
Replay buffer size	10,000
Exploration strategy	Epsilon-Greedy
Exploration decay rate	0.99
Discount factor (gamma)	0.99
Target network update frequency	1000
Soft target update rate (tau)	0.01
Regularization (L2 weight decay)	0.0001
Gradient clipping threshold	1.0
Double DQN	Yes
Prioritized experience replay (PER)	Yes
Dueling DQN	Yes
Multistep learning	3
Training time	39 h

.

5. Results and Discussion

To conduct a comprehensive analysis, this study evaluated and simulated multiple performance metrics and compared them with a compilation of current methods to assess the study’s robustness. It is worth noting that since the experiments are simulation-based, the real-time results for current methods may vary slightly. Nonetheless, the study provides a complete overview of the developed model and its significance. The graphical analysis of Current Method-1, Current Method-2, and Current Method-3 presents a compilation of various studies [23,24,25,26,27,28,29] and their results for comparison. The key difference between the proposed study and aforementioned studies is that they are mostly employed in 5G systems, whereas the proposed work was tested in a 6G simulated environment. The reason for comparing with the 5G studies is to provide an overview of the efficiency analysis of the upcoming 6G networks. Furthermore, the study does not directly compare its results with the graphs presented in the aforementioned studies, but rather performs a detailed analysis and extraction of the relevant results. Performance metrics that are analyzed in this section are as follows:

• Throughput;
• Latency;
• Reliability;
• Spectral efficiency;
• Beam-alignment error;
• Beam-switching rate;
• Coverage probability;
• Interference levels;
• Doppler shift for fast speed vehicles;
• Energy consumption and resource utilization;
• Network scalability;
• SINR value.

The proposed system model incorporating switched beam antenna and deep reinforcement learning (DRL) achieved a significant increase in throughput compared to the three other methods. The improved performance can be attributed to the DRL agent’s capability to learn from the communication environment and make informed decisions on the optimal beam pattern for transmission. By continuously updating its knowledge of the channel state information (CSI), the DRL agent ensures the most efficient data transfer, leading to higher throughput compared to the existing methods as shown in Figure 4.

Our proposed approach has a relatively low throughput in a holistic analysis, as the expected throughput for 6G systems can range from tens to hundreds of Gbps. As a result, in challenging scenarios, the achievable throughput may be lower than the ideal target. Additionally, this approach focuses on addressing multiple problems on a small scale, limiting the measurement of throughput to Mbps rather than Gbps. To further investigate the cause of the low throughput, we analyzed underlying conditions and introduced additional parameters, as shown in

Table 4. Additional parameters to cross-check throughput analysis.

Parameter	Value
Packet loss rate	3%
Link adaptation strategy	Adaptive MCS

, to cross-verify the model.

Upon analysis, the packet loss rate was determined to be approximately 3%. With a packet loss rate of 3%, a significant number of transmitted packets are not successfully decoded at the receiver, which is attributed to factors such as multipath fading and nonlinear distortion. The impact of a 3% packet loss rate varies depending on the situation. For example, in real-time voice or video communication, a 3% packet loss rate results in noticeable degradation of the received data quality. However, for applications such as file transfers, a 3% packet loss rate is acceptable as lost packets can be retransmitted without affecting the overall user experience.

The proposed system model, which employs a switched beam antenna and deep reinforcement learning, considers a 3% packet loss rate as moderately high. This is because 6G networks aim to provide ultra-reliable and low-latency communication (URLLC). In vehicle-to-vehicle (V2V) communication scenarios, especially for safety-critical applications, reliability and low latency are crucial. A high packet loss rate indicates that a significant number of transmitted packets are not correctly received at the destination, resulting in retransmissions that consume valuable network resources and decrease overall throughput, contributing to low throughput.

Secondly, the system employs an adaptive modulation and coding scheme (MCS) for its link adaptation strategy. This enables the system to optimize its modulation and coding schemes based on current channel conditions. However, this may result in lower throughput in certain scenarios as the system may prioritize link reliability by choosing more robust but less spectrally efficient MCS options. The deep reinforcement learning agent may also temporarily select suboptimal MCS options before finding a more optimal solution, which can also contribute to lower throughput.

By optimizing beam-switching decisions, the system can adapt to rapid changes in channel conditions and interference, minimizing delays in data transmission and reducing overall latency. The proposed 6G system exhibits lower latency than the other methods due to the DRL agent’s real-time decision-making capabilities and the inherent low latency of 6G technologies. The combination of these factors allows for the rapid adaptation of beam-switching decisions in highly dynamic V2V environments. As a result, the system can maintain strong communication links and minimize delays in data transmission, even in the presence of rapid channel variations and interference. As shown in Figure 5, we can observe that the latency of the proposed method is marked as the lowest at the 58th second, which is 10.2 ms.

The reliability of the proposed 6G system is significantly higher than the other methods, as the switched beam antenna and the DRL agent work together to maintain robust communication links. The integration of 6G technologies, such as advanced error correction codes and massive MIMO, enhances the resilience of the system to packet loss and link failures. Consequently, the proposed system offers improved reliability in the challenging communication scenarios typical of 6G V2V networks. Results are illustrated in Figure 6.

The proposed system outperforms the other methods in terms of spectral efficiency, as the intelligent beam-switching and adaptive antenna configurations enabled by the DRL agent allow for more efficient use of the 6G frequency spectrum. The system can maximize data transmission rates within the limited spectrum, providing superior spectral efficiency compared to the other methods as shown in Figure 7.

When a switched beam antenna is switched from one beam direction to another, the beam-alignment error can cause the signal to be misdirected, leading to reduced signal quality and potential signal loss. This can be particularly problematic in high-speed mobile networks, where beam switching must be performed quickly to maintain communication with a moving device. In this conducted research, beam-alignment error is significantly reduced by using the advance technique of the switched beam antenna and system model of deep reinforcement learning. Furthermore, the proposed approach after extensive experimentation tends to produce low levels of error approaching less than 5 degrees on average by increasing number of time, which shows the stability of the model, as shown in Figure 8.

Beam-switching rate is a measure of the speed at which a switched beam antenna can change its beam direction. In switched beam antennas, the beam direction can be changed electronically, allowing the antenna to steer its beam in a specific direction to provide directional transmission and reception of signals. The beam-switching rate is an important factor in switched beam antennas because it determines the speed at which the antenna can respond to changes in the location of the device it is communicating with. In high-speed mobile networks, for example, a fast beam-switching rate is necessary to maintain communication with a moving device and ensure that the signal remains strong and reliable. A high beam-switching rate also allows the antenna to support multiple users by quickly switching between beams to provide directional transmission and reception to each user. This can be particularly important in dense urban environments, where multiple users may be present in a small area, and in satellite communications, where multiple beams may be required to cover a large geographic area. To achieve a fast beam-switching rate, we incorporated the system model with advance reinforcement leanings, and the switching rate, on average, of the proposed method tended to be at the lower end, which shows the robustness of the model. Results are illustrated in Figure 9. The proposed method approaches switching rates as low as 2.4 switches/seconds, which is reliable for high-speed V2V communication. Frequent beam switching, however, affects the system throughput. Every time a beam switch occurs, there is a period during which the system has to adjust to the new beam configuration, potentially leading to a temporary reduction in throughput as the system may not operate at its full capacity during the adaptation process.

The coverage probability results for the proposed system model, which integrates a switched beam antenna with a 6G V2V communication system and leverages deep reinforcement learning (DRL) for real-time adaptation, provide valuable insights into the system’s performance. In the simulation, we assessed the coverage probability under various scenarios, considering dynamic vehicular environments, diverse channel conditions, and different network loads. The coverage probability is calculated as the ratio of the number of successful communication links (i.e., links with a signal-to-interference-plus-noise ratio (SINR) above a predefined threshold) to the total number of communication links in the network. The results indicate that the proposed system consistently achieves higher coverage probability values compared to the existing state-of-the-art methods. This improvement is primarily due to the DRL-based adaptive beamforming, which allows the system to intelligently select the optimal beam direction and adapt to changing channel conditions. The switched beam antenna’s capability to steer the radiation pattern towards the intended receiver, while mitigating interference from other sources, further enhances the coverage probability. A detailed analysis of the results demonstrates that the proposed system model is more resilient to the challenges posed by dynamic vehicular environments, such as user mobility, shadowing, and multipath fading. The increased coverage probability achieved by the integrated system model implies that users in the 6G V2V communication network are more likely to maintain a high-quality communication link, leading to improved network performance, reliability, and user satisfaction, as shown in Figure 10.

The interference level experienced by the proposed system is lower compared to the other methods. The DRL model’s ability to learn and adapt to the communication environment enables the system to make informed decisions on beam pattern selection that minimize interference. This reduces the impact of neighboring vehicles and other sources of interference on the communication link, ensuring better signal quality and overall performance, as shown in Figure 11.

An improved ability to handle the Doppler shift compared to the other methods is observed. The DRL agent’s real-time decision-making capabilities allow the system to rapidly adapt to changing channel conditions caused by the relative motion of vehicles. By continuously updating its knowledge of the channel state information (CSI) and making optimal beam-switching decisions, the system can maintain a stable communication link even in the presence of significant Doppler shifts, as shown in Figure 12.

According to Figure 13, at an interference level of 20 dB, the average reward over 5000 episodes was 20. This shows that the agent was able to perform well in the environment and receive a high level of rewards. The high average reward indicates that the agent is able to effectively navigate the environment and achieve its goals despite the presence of interference. Overall, these results suggest that the level of interference has a significant impact on the agent’s performance and the rewards it receives. The results also highlight the importance of considering the impact of interference when designing and evaluating reinforcement learning systems in V2V environments.

The energy efficiency of the proposed 6G system is improved compared to the other methods. The DRL agent optimizes beam-switching decisions in such a way that it reduces unnecessary energy consumption while maintaining high-performance communication links. The incorporation of 6G technologies, such as advanced power control schemes and energy-efficient hardware, further enhances the system’s energy efficiency. Similarly, the proposed 6G system model demonstrates more efficient resource utilization than the other methods. The DRL agent’s ability to adapt and optimize beam-switching decisions based on the current communication environment enables the system to utilize the available resources more effectively. By minimizing the interference between the vehicles and reducing the overhead associated with suboptimal beam patterns, the system ensures efficient use of the advanced resources provided by 6G communication systems. Results can be observed in Figure 14 and Figure 15.

The proposed 6G system exhibits better network scalability as the number of nodes in the V2V communication environment increases. The DRL model’s continuous learning and adaptation capabilities, combined with 6G technologies such as network slicing and edge computing, ensure that the system can handle more complex scenarios without a significant loss in performance. This feature is essential for supporting the increased density of connected vehicles and devices expected in future 6G V2V networks. Scalability is tested on 5000 vehicular nodes to check the robustness of the system in highly dense environments. Scalability contains average resource utilization in bits per second per Hertz (bps/Hz); it is a measure of the efficiency of a communication system in terms of the amount of data that can be transmitted per unit of bandwidth. In general, higher average resource utilization indicates that the communication system is more efficient in terms of the amount of data that can be transmitted per unit of bandwidth, and can result in improved performance and higher data rates. This is especially important in modern wireless communication systems, where bandwidth is a scarce and valuable resource, and the demand for high-speed data transmission continues to grow. As can be seen in Figure 16, average resource utilization in bps/Hz is very stabilized between 5300 and 5260, which is considered stable in modern communication depending on use case.

The graph illustrated in Figure 17 demonstrates a gradual decrease in SINR from approximately 80 dB to 19 dB as the distance between the transmitter and the receiver increases from 0 to 100 m. As the distance between the transmitter and the receiver increases, the path loss also increases, leading to a weaker received signal strength at the receiver. Consequently, the SINR decreases as the distance increases. Furthermore, at shorter distances (closer to the transmitter), the SINR is relatively high (around 140 dB), indicating that the signal strength is much stronger than the noise level. In this region, the communication link quality is expected to be excellent, enabling high data rates and reliable communication. As the distance increases, the SINR gradually decreases, reaching approximately 19 dB at 100 m. Even at this distance, the SINR is still relatively high compared to typical wireless communication systems, suggesting that the communication V2V link quality is still good.

There are certain assumptions of the proposed model which can develop certain limitations in real time implementation, such as:

• It is assumed that the transmitter and receiver have perfect knowledge of the channel conditions. However, in practice, CSI is estimated and subject to errors, which can affect the performance of the system.
• In a real-time V2V communication system, synchronization between the transmitter and receiver is crucial for accurate beam tracking and alignment. This research assumed perfect synchronization, which might not be the case in real-world scenarios.
• The performance of the proposed system is dependent on the specific channel model used in the simulations. In practice, the actual channel conditions might be more complex and diverse, which can affect the system’s performance.
• The proposed model assumed certain mobility patterns for the vehicles, while in practice, the vehicular mobility can be more complex, involving varying speeds and unpredictable movements.

6. Conclusions

In conclusion, this study presented a comprehensive system model that integrates advanced switched beam antenna technology with 6G V2V communication systems, utilizing deep reinforcement learning (DRL) for real-time adaptation and learning. By employing the 6G channel model, the proposed system effectively accounts for the dynamic nature of vehicular environments, including path loss, shadowing, and multipath fading effects. The DRL model enables the system to intelligently select the optimal beam direction, resource allocation, and interference management, optimizing performance metrics such as throughput, latency, reliability, and spectral efficiency. The results of the simulation demonstrate the superiority of the proposed system model in comparison to existing methods, highlighting significant improvements in key performance indicators. The proposed system exhibits reduced beam-alignment error, lower beam-switching rates, increased coverage probability, and enhanced resilience to interference and Doppler shifts. Moreover, the integration of the 6G channel model and switched beam antenna system showcases the potential for synergistic advancements in the field of V2V communications. Overall, the proposed system model and its accompanying algorithms exhibit a promising framework for future 6G V2V communication systems. The real-time adaptation and learning facilitated by DRL, combined with the advanced features of 6G and switched beam antenna technology, pave the way for highly efficient, reliable, and scalable vehicular communication networks. Further research in this area could explore additional performance enhancements, novel application scenarios, and the integration of emerging technologies, driving the evolution of next-generation communication systems.