Pruning Multi-Scale Multi-Branch Network for Small-Sample Hyperspectral Image Classification
Abstract
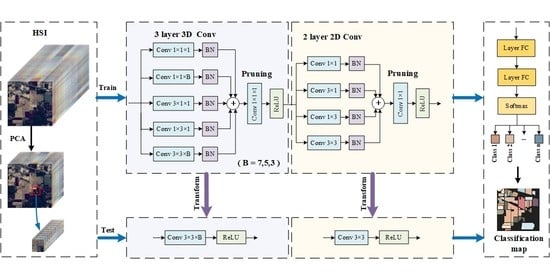
:1. Introduction
- To improve the classification accuracy of small training samples, based on DBB, MSMBB and 3D-MSMBB are proposed. In the training phase, these two modules combine the structural features of asymmetric convolution and multi-branching to explore complementary information through different sensory fields, to achieve adequate feature extraction for small-sample datasets. In the testing phase, MSMBB and 3D-MSMBB are equivalently transformed into a single convolutional layer for deployment, to reduce test resource consumption.
- To reduce the size of the network model, without significantly affecting the classification accuracy, we introduce pruning modules in the master branch of each MSMBB and 3D-MSMBB. The size of the MSMBB and 3D-MSMBB transformed convolutional layers is reduced by pruning the input channels of the pruning module, thus reducing the computational effort of the network.
- To the best of our knowledge, our method combines DBB with pruning for the first time and extends it to 3D-CNN for HSI classification. The experimental results show that the method can obtain better classification results with a smaller number of training samples and resolve the problem of low classification accuracy for small-sample datasets, as well as achieving a lightweight model.
2. Materials and Methods
2.1. Proposed Method
2.2. MSMBB and 3D-MSMBB
2.2.1. MSMBB
2.2.2. 3D-MSMBB
2.3. Pruning Multi-Scale Multi-Branch Block
2.4. Overall Algorithm Steps
| Algorithm 1. PMSMBN model |
| Input: HSI data , number of bands = Output: Classification map of the test set |
| 1. Obtain after PCA, is divided into multiple overlapping 3D patches, with the number . |
| 2. Randomly divide the 3D patches into a training set and test set according to the proportion of training and testing. |
| 3. For in epoch; |
| 4. Extract spectral–spatial features through three 3D-PMSMBBs and two PMSMBBs. |
| 5. Flatten the 2D feature map into a 1D feature vector. |
| 6. Input the 1D feature vector into two linear layers. |
| 7. Use softmax to classify and obtain classification results. |
| 8. Calculate the score of each channel of each pruning part and modify the mask according to the result. |
| 9. Transform the training model into the test model. |
| 10. Use the test set with the test model to obtain predicted labels. |
3. Experimental Results and Analysis
3.1. Hyperspectral Dataset
3.2. Experimental Setting
3.3. Experimental Results and Analysis
3.4. Ablation Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, Z.; Xu, B.; Sun, L.; Zhan, T.; Tang, S. 3-D Channel and Spatial Attention Based Multiscale Spatial–Spectral Residual Network for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4311–4324. [Google Scholar] [CrossRef]
- Shi, Q.; Tang, X.; Yang, T.; Liu, R.; Zhang, L. Hyperspectral Image Denoising Using a 3-D Attention Denoising Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10348–10363. [Google Scholar] [CrossRef]
- Tian, S.; Lu, Q.; Wei, L. Multiscale Superpixel-Based Fine Classification of Crops in the UAV-Based Hyperspectral Imagery. Remote Sens. 2022, 14, 3292. [Google Scholar] [CrossRef]
- Yadav, C.S.; Pradhan, M.K.; Gangadharan, S.M.P.; Chaudhary, J.K.; Singh, J.; Khan, A.A.; Haq, M.A.; Alhussen, A.; Wechtaisong, C.; Imran, H.; et al. Multi-Class Pixel Certainty Active Learning Model for Classification of Land Cover Classes Using Hyperspectral Imagery. Electronics 2022, 11, 2799. [Google Scholar] [CrossRef]
- Fang, C.; Han, Y.; Weng, F. Monitoring Asian Dust Storms from NOAA-20 CrIS Double CO2 Band Observations. Remote Sens. 2022, 14, 4659. [Google Scholar] [CrossRef]
- Han, X.; Zhang, H.; Sun, W. Spectral Anomaly Detection Based on Dictionary Learning for Sea Surfaces. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, Z.; He, M.; Ye, Z.; Xu, K.; Nian, Y.; Huang, B. Reconstruction of Hyperspectral Images from Spectral Compressed Sensing Based on a Multitype Mixing Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2304–2320. [Google Scholar] [CrossRef]
- Yu, C.; Han, R.; Song, M.; Liu, C.; Chang, C.-I. Feedback Attention-Based Dense CNN for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of Hyperspectral Remote Sensing Images with Support Vector Machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Crawford, M.M.; Tian, J. Local Manifold Learning-Based k-Nearest-Neighbor for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–Spatial Hyperspectral Image Segmentation Using Subspace Multinomial Logistic Regression and Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Qian, Y.; Ye, M.; Zhou, J. Hyperspectral Image Classification Based on Structured Sparse Logistic Regression and Three-Dimensional Wavelet Texture Features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2276–2291. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Jia, S.; He, S.; Sun, Y.; Ji, Z.; Shen, L. Three-Dimensional Gabor Feature Extraction for Hyperspectral Imagery Classification Using a Memetic Framework. Inf. Sci. 2015, 298, 274–287. [Google Scholar] [CrossRef]
- Dundar, T.; Ince, T. Sparse Representation-Based Hyperspectral Image Classification Using Multiscale Superpixels and Guided Filter. IEEE Geosci. Remote Sens. Lett. 2019, 16, 246–250. [Google Scholar] [CrossRef]
- Duan, P.; Kang, X.; Li, S.; Ghamisi, P.; Benediktsson, J.A. Fusion of Multiple Edge-Preserving Operations for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10336–10349. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, G.; Jia, X.; Wu, L.; Zhang, A.; Ren, J.; Fu, H.; Yao, Y. Spectral–Spatial Self-Attention Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Zheng, J.; Feng, Y.; Bai, C.; Zhang, J. Hyperspectral Image Classification Using Mixed Convolutions and Covariance Pooling. IEEE Trans. Geosci. Remote Sens. 2021, 59, 522–534. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; He, X.; Li, Z. Soft Augmentation-Based Siamese CNN for Hyperspectral Image Classification with Limited Training Samples. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Chanussot, J. Convolutional Neural Networks for Multimodal Remote Sensing Data Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–10. [Google Scholar] [CrossRef]
- Sultana, F.; Sufian, A.; Dutta, P. Evolution of Image Segmentation Using Deep Convolutional Neural Network: A Survey. Knowl. -Based Syst. 2020, 201–202, 106062. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, e258619. [Google Scholar] [CrossRef] [Green Version]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep Supervised Learning for Hyperspectral Data Classification through Convolutional Neural Networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Fang, L.; Liu, Z.; Song, W. Deep Hashing Neural Networks for Hyperspectral Image Feature Extraction. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1412–1416. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A Fast Dense Spectral–Spatial Convolution Network Framework for Hyperspectral Images Classification. Remote Sens. 2018, 10, 1068. [Google Scholar] [CrossRef] [Green Version]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.; Li, J.; Pla, F. Capsule Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2145–2160. [Google Scholar] [CrossRef]
- Tinega, H.C.; Chen, E.; Ma, L.; Nyasaka, D.O.; Mariita, R.M. HybridGBN-SR: A Deep 3D/2D Genome Graph-Based Network for Hyperspectral Image Classification. Remote Sens. 2022, 14, 1332. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef] [Green Version]
- Zhu, M.; Jiao, L.; Liu, F.; Yang, S.; Wang, J. Residual Spectral–Spatial Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 449–462. [Google Scholar] [CrossRef]
- Wu, H.; Li, D.; Wang, Y.; Li, X.; Kong, F.; Wang, Q. Hyperspectral Image Classification Based on Two-Branch Spectral–Spatial-Feature Attention Network. Remote Sens. 2021, 13, 4262. [Google Scholar] [CrossRef]
- Hang, R.; Li, Z.; Liu, Q.; Ghamisi, P.; Bhattacharyya, S.S. Hyperspectral Image Classification with Attention-Aided CNNs. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2281–2293. [Google Scholar] [CrossRef]
- Sun, H.; Zheng, X.; Lu, X.; Wu, S. Spectral–Spatial Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3232–3245. [Google Scholar] [CrossRef]
- Dong, Z.; Cai, Y.; Cai, Z.; Liu, X.; Yang, Z.; Zhuge, M. Cooperative Spectral–Spatial Attention Dense Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 866–870. [Google Scholar] [CrossRef]
- Xiang, J.; Wei, C.; Wang, M.; Teng, L. End-to-End Multilevel Hybrid Attention Framework for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, X.; Han, J.; Ding, G. Diverse Branch Block: Building a Convolution as an Inception-like Unit. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10881–10890. [Google Scholar]
- Ding, X.; Hao, T.; Tan, J.; Liu, J.; Han, J.; Guo, Y.; Ding, G. ResRep: Lossless CNN Pruning via Decoupling Remembering and Forgetting. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 4490–4500. [Google Scholar]
- Ding, X.; Ding, G.; Zhou, X.; Guo, Y.; Han, J.; Liu, J. Global Sparse Momentum SGD for Pruning Very Deep Neural Networks. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar] [CrossRef]
- Licciardi, G.; Marpu, P.R.; Chanussot, J.; Benediktsson, J.A. Linear Versus Nonlinear PCA for the Classification of Hyperspectral Data Based on the Extended Morphological Profiles. IEEE Geosci. Remote Sens. Lett. 2012, 9, 447–451. [Google Scholar] [CrossRef] [Green Version]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral Image Classification with Independent Component Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef] [Green Version]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of Hyperspectral Images with Regularized Linear Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Ghaffari, M.; Omidikia, N.; Ruckebusch, C. Essential Spectral Pixels for Multivariate Curve Resolution of Chemical Images. Anal. Chem. 2019, 91, 10943–10948. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, K.; Wu, S.; Shi, H.; Zhao, Y.; Sun, Y.; Zhuang, H.; Fu, E. An Investigation of a Multidimensional CNN Combined with an Attention Mechanism Model to Resolve Small-Sample Problems in Hyperspectral Image Classification. Remote Sens. 2022, 14, 785. [Google Scholar] [CrossRef]
- Feng, Y.; Zheng, J.; Qin, M.; Bai, C.; Zhang, J. 3D Octave and 2D Vanilla Mixed Convolutional Neural Network for Hyperspectral Image Classification with Limited Samples. Remote Sens. 2021, 13, 4407. [Google Scholar] [CrossRef]
- Ding, X.; Guo, Y.; Ding, G.; Han, J. ACNet: Strengthening the Kernel Skeletons for Powerful CNN via Asymmetric Convolution Blocks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1911–1920. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 448–456. [Google Scholar]













| Class | 2D-CNN [27] (2015) | 3D-CNN [30] (2016) | SSRN [31] (2018) | HybridSN [35] (2020) | SSAN [39] (2020) | DMCN [41] (2022) | PMSMBN |
|---|---|---|---|---|---|---|---|
| 1 | 50.02 | 65.08 | 73.68 | 96.77 | 67.74 | 68.29 | 89.36 |
| 2 | 73.70 | 76.51 | 83.25 | 86.88 | 84.45 | 87.95 | 95.04 |
| 3 | 75.07 | 98.39 | 88.44 | 85.30 | 92.05 | 91.81 | 95.76 |
| 4 | 98.16 | 98.11 | 77.49 | 98.59 | 91.81 | 98.88 | 98.46 |
| 5 | 89.85 | 81.01 | 97.33 | 99.48 | 97.84 | 97.14 | 95.37 |
| 6 | 87.61 | 92.95 | 86.56 | 92.58 | 93.63 | 89.78 | 93.11 |
| 7 | 99.21 | 99.73 | 99.62 | 99.36 | 99.88 | 95.83 | 99.96 |
| 8 | 90.91 | 98.73 | 96.54 | 98.89 | 99.54 | 96.93 | 99.89 |
| 9 | 56.03 | 80.00 | 72.22 | 88.89 | 76.19 | 64.71 | 99.89 |
| 10 | 89.49 | 97.25 | 90.48 | 89.50 | 91.75 | 89.90 | 96.36 |
| 11 | 78.47 | 73.77 | 93.79 | 91.75 | 92.49 | 93.32 | 96.78 |
| 12 | 74.84 | 67.23 | 88.50 | 82.47 | 91.09 | 90.68 | 94.92 |
| 13 | 98.56 | 88.12 | 98.37 | 94.29 | 96.74 | 99.76 | 99.86 |
| 14 | 97.77 | 96.40 | 92.89 | 91.37 | 92.67 | 98.70 | 99.30 |
| 15 | 97.73 | 97.66 | 87.87 | 97.82 | 78.24 | 96.47 | 96.06 |
| 16 | 87.50 | 71.31 | 98.72 | 73.87 | 77.27 | 97.59 | 80.19 |
| OA | 83.36 ± 1.66 | 83.30 ± 1.63 | 90.29 ± 0.57 | 90.57 ± 0.33 | 91.02 ± 0.22 | 92.92 ± 0.54 | 96.28 ± 0.46 |
| AA | 84.31 ± 0.53 | 86.82 ± 1.55 | 89.13 ± 0.36 | 91.78 ± 0.57 | 89.00 ± 0.75 | 91.12 ± 0.61 | 95.67 ± 0.68 |
| Kappa | 80.88 ± 1.66 | 80.72 ± 1.48 | 88.92 ± 0.13 | 89.20 ± 0.58 | 89.75 ± 0.98 | 91.91 ± 0.40 | 95.76 ± 0.44 |
| Class | 2D-CNN [27] (2015) | 3D-CNN [30] (2016) | SSRN [31] (2018) | HybridSN [35] (2020) | SSAN [39] (2020) | DMCN [41] (2022) | PMSMBN |
|---|---|---|---|---|---|---|---|
| 1 | 76.65 | 71.47 | 94.53 | 93.82 | 84.74 | 94.63 | 96.09 |
| 2 | 94.91 | 92.72 | 94.97 | 98.60 | 97.92 | 99.08 | 99.44 |
| 3 | 89.88 | 83.80 | 88.61 | 90.08 | 90.20 | 89.11 | 94.75 |
| 4 | 87.83 | 98.09 | 98.71 | 95.43 | 95.31 | 98.52 | 98.04 |
| 5 | 99.35 | 99.66 | 99.39 | 99.92 | 99.89 | 97.77 | 100.00 |
| 6 | 98.45 | 95.16 | 98.64 | 99.19 | 98.17 | 99.52 | 99.31 |
| 7 | 89.00 | 97.24 | 89.26 | 92.28 | 95.19 | 97.68 | 92.51 |
| 8 | 67.63 | 72.63 | 78.79 | 83.54 | 88.46 | 93.74 | 92.20 |
| 9 | 16.35 | 71.73 | 96.69 | 88.05 | 96.42 | 89.68 | 95.98 |
| OA | 84.01 ± 0.66 | 87.31 ± 0.44 | 93.62 ± 0.46 | 95.59 ± 0.03 | 94.26 ± 0.25 | 97.18 ± 0.67 | 97.67 ± 0.72 |
| AA | 76.67 ± 0.53 | 87.29 ± 0.30 | 93.29 ± 024 | 93.43 ± 0.41 | 94.05 ± 0.45 | 95.53 ± 0.22 | 96.48 ± 0.85 |
| Kappa | 78.67 ± 0.68 | 82.80 ± 0.29 | 91.44 ± 0.44 | 94.13 ± 0.16 | 92.34 ± 0.23 | 96.25 ± 0.49 | 96.90 ± 0.33 |
| Class | 2D-CNN [27] (2015) | 3D-CNN [30] (2016) | SSRN [31] (2018) | HybridSN [35] (2020) | SSAN [39] (2020) | DMCN [41] (2022) | PMSMBN |
|---|---|---|---|---|---|---|---|
| 1 | 99.95 | 99.96 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 2 | 98.23 | 98.90 | 99.43 | 100.00 | 98.84 | 99.92 | 100.00 |
| 3 | 98.59 | 97.54 | 100.00 | 99.86 | 99.64 | 100.00 | 100.00 |
| 4 | 98.15 | 89.88 | 96.93 | 77.97 | 99.17 | 99.85 | 100.00 |
| 5 | 96.61 | 98.84 | 98.11 | 99.95 | 97.41 | 99.80 | 98.98 |
| 6 | 93.80 | 99.51 | 97.82 | 99.70 | 97.21 | 99.84 | 100.00 |
| 7 | 98.94 | 99.54 | 99.92 | 99.61 | 99.94 | 99.97 | 99.92 |
| 8 | 84.75 | 92.79 | 91.15 | 99.49 | 98.93 | 95.78 | 99.90 |
| 9 | 91.25 | 99.87 | 99.32 | 99.89 | 99.37 | 99.93 | 100.00 |
| 10 | 99.47 | 95.66 | 98.55 | 99.16 | 100.00 | 99.94 | 99.91 |
| 11 | 96.80 | 89.37 | 99.27 | 97.00 | 99.06 | 99.90 | 100.00 |
| 12 | 99.66 | 98.71 | 99.84 | 99.14 | 99.57 | 100.00 | 98.85 |
| 13 | 81.03 | 75.23 | 95.31 | 98.00 | 99.53 | 97.85 | 99.67 |
| 14 | 87.25 | 96.41 | 88.32 | 98.44 | 84.16 | 99.61 | 99.62 |
| 15 | 87.90 | 99.97 | 98.83 | 98.85 | 99.02 | 99.23 | 99.35 |
| 16 | 99.64 | 97.76 | 99.72 | 100.00 | 100.00 | 100.00 | 100.00 |
| OA | 92.41 ± 0.22 | 95.70 ± 0.34 | 97.09 ± 0.33 | 98.19 ± 0.60 | 98.38 ± 0.28 | 98.98 ± 0.35 | 99.78 ± 0.19 |
| AA | 94.52 ± 0.81 | 95.86 ± 0.79 | 97.79 ± 0.58 | 97.26 ± 0.47 | 97.40 ± 0.39 | 99.13 ± 0.62 | 99.76 ± 0.13 |
| Kappa | 91.54 ± 0.53 | 96.33 ± 0.63 | 96.76 ± 0.47 | 97.98 ± 0.16 | 98.19 ± 0.44 | 98.88 ± 0.39 | 99.76 ± 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Xu, M.; Zhang, L.; Liu, Y. Pruning Multi-Scale Multi-Branch Network for Small-Sample Hyperspectral Image Classification. Electronics 2023, 12, 674. https://doi.org/10.3390/electronics12030674
Bai Y, Xu M, Zhang L, Liu Y. Pruning Multi-Scale Multi-Branch Network for Small-Sample Hyperspectral Image Classification. Electronics. 2023; 12(3):674. https://doi.org/10.3390/electronics12030674
Chicago/Turabian StyleBai, Yu, Meng Xu, Lili Zhang, and Yuxuan Liu. 2023. "Pruning Multi-Scale Multi-Branch Network for Small-Sample Hyperspectral Image Classification" Electronics 12, no. 3: 674. https://doi.org/10.3390/electronics12030674
APA StyleBai, Y., Xu, M., Zhang, L., & Liu, Y. (2023). Pruning Multi-Scale Multi-Branch Network for Small-Sample Hyperspectral Image Classification. Electronics, 12(3), 674. https://doi.org/10.3390/electronics12030674