Spline Function Simulation Data Generation for Walking Motion Using Foot-Mounted Inertial Sensors

Abstract

This paper investigates the generation of simulation data for motion estimation using inertial sensors. The smoothing algorithm with waypoint-based map matching is proposed using foot-mounted inertial sensors to estimate position and attitude. The simulation data are generated using spline functions, where the estimated position and attitude are used as control points. The attitude is represented using B-spline quaternion and the position is represented by eighth-order algebraic splines. The simulation data can be generated using inertial sensors (accelerometer and gyroscope) without using any additional sensors. Through indoor experiments, two scenarios were examined include 2D walking path (rectangular) and 3D walking path (corridor and stairs) for simulation data generation. The proposed simulation data is used to evaluate the estimation performance with different parameters such as different noise levels and sampling periods.

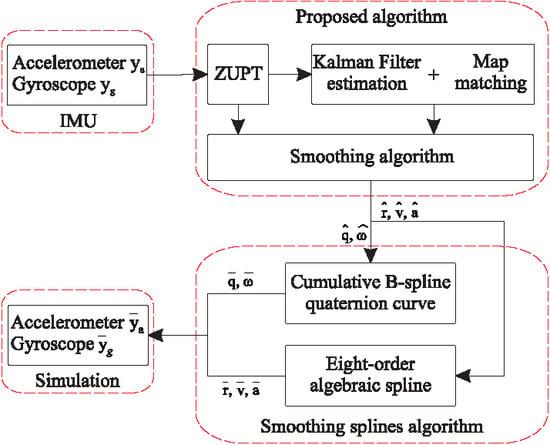
1. Introduction

Motion estimation using inertial sensors is one of the most important research topics that is increasingly applied in many application areas such as medical applications, sports, and entertainment [1]. Inertial measurement unit (IMU) sensors are commonly used to estimate human motion [2,3,4,5]. Inertial sensors can be used alone or combined with other sensors such as cameras [6,7] or magnetic sensors [8]. In personal navigation and healthcare applications [9,10,11], foot-mounted inertial sensors without using any additional sensors is a key enabling technology since it does not require any additional infrastructure. If additional sensors (other than inertial sensors) are also used, sensor fusion algorithms [12,13] can be used to obtain more accurate motion estimation.

To evaluate the accuracy of any motion estimation algorithm, it is necessary to compare the estimated value with the true value. The estimated value is usually verified through experiments with both IMU and optical motion tracker [14,15]. In [2], the Vicon optical motion capture system is used to evaluate the effectiveness of human pose estimation method and its associated sensor calibration procedure. An optical motion tracking is used as a reference to compare with motion estimation using inertial sensors in [15].

Although the experimental validation gives the ultimate proof, it is not only more convenient but also more important to work with simulation data, which is statistically much more relevant for testing and the development of algorithms. For example, the effect of gyroscope bias on the performance of an algorithm cannot be easily identified in experiments. In this case, simulation using synthesized data is more convenient since gyroscope bias can be changed arbitrarily.

In [16,17,18], IMU simulation data are generated using optical motion capture data for human motion estimation. In [19], IMU simulation data is generated for walking motion by approximating walking trajectory as simple sinusoidal functions. In [20,21,22], IMU simulation data are also generated for flight motion estimation using an artificially generated trajectory. There are many different methods to represent attitude and position simulation data. Among them, the spline function is the most popular approach [23]. The B-spline quaternion algorithm provides a general curve construction scheme that extends the spline curves [24]. Reference [25] presents an approach for attitude estimation using cumulative B-splines unit quaternion curves. Position can be represented by any spline function [23]. Usually, position data are represented using cubic spline functions. The cubic spline function gives a continuous position, velocity, and acceleration. However, the acceleration is not sufficiently smooth. This is a problem for the inertial sensor simulation data generation since the smooth accelerometer data cannot be generated. Thus, we use the eighth-order spline function for position data since it gives position data with smooth acceleration, whose jerk (third derivative) can be controlled in the optimization problem.

In this paper, we use cumulative B-spline for attitude representation and eighth-order algebraic spline for position representation. The eighth-order algebraic spline is a slightly modified version of the spline function from a previous study [26].

The aim of this paper is to obtain simulation data combining inertial sensors (accelerometer and gyroscope) and waypoint data without using any additional sensors. A computationally efficient waypoint-based map matching smoothing algorithm is proposed for position and attitude estimation from foot-mounted inertial sensors. The simulation data are generated using spline functions, where the estimated position and attitude are used as control points. This paper is an extended version of a work published in the conference paper [27], where a basic algorithm with a simple experimental result is given.

The remainder of the paper is organized as follows. Section 2 describes the smoothing algorithm with waypoint-based map matching to estimate motion for foot-mounted inertial sensors. Section 3 describes the computation of the spline function to generate simulation data. Section 4 provides the experiment results to verify the proposed method. Conclusions are given in Section 5.

2. Smoothing Algorithm with Waypoint-Based Map Matching

In this section, a smoothing algorithm is proposed to estimate the attitude, position, velocity and acceleration, which will be used to generate simulation data in Section 3.

Two coordinate frames are used in this paper: the body coordinate frame and the navigation coordinate frame. The three axes of the body coordinate frame coincide with the three axes of the IMU. The z axis of the navigation coordinate frame coincides with the local gravitational direction. The choice of the x and y axes of the navigation coordinate frame can be arbitrarily chosen. The notation ${\left[p\right]}_n$ $\left({\left[p\right]}_b\right)$ is used to denote that a vector p is represented in the navigation (body) coordinate frame.

The position is defined by ${\left[r\right]}_n\in R^3$, which is the origin of the body coordinate frame expressed in the navigation coordinate frame. Similarly, the velocity and the acceleration are denoted by ${\left[v\right]}_n\in R^3$ and ${\left[a\right]}_n\in R^3$, respectively. The attitude is represented using a quaternion $q\in R^4$, which represents the rotation relationship between the navigation coordinate frame and the body coordinate frame. The directional cosine matrix corresponding to quaternion q is denoted by $C\left(q\right)\in SO\left(3\right)$.

The accelerometer output $y_a\in R^3$ and the gyroscope output $y_g\in R^3$ are given by

$$\begin{array}{c}{y}_a=C\left(q\right)\tilde{g}+a_b+n_a,\hfill \\ y_g=\omega +n_g,\hfill \end{array}$$

(1)

where $\omega \in R^3$ is the angular velocity, $a_b\in R^3$ is the external acceleration (acceleration related to the movement, excluding the gravitational acceleration) expressed in the body coordinate frame, and $n_a\in R^3$ and $n_g\in R^3$ are sensor noises. The vector $\tilde{g}$ is the local gravitational acceleration vector. It is assumed that $\tilde{g}$ is known, which can be computed using the formula in [28]. The sensor biases are assumed to be estimated separately using calibration algorithms [29,30].

Let T denote the sampling period of a sensor. For a continuous time signal $y\left(t\right)$, the discrete value is denoted by $y_k=y\left(kT\right)$. The discrete sensor noise $n_{a,k}$ and $n_{g,k}$ are assumed to be white Gaussian sensor noises, whose covariances are given by

$$\begin{array}{c}{R}_a=\mathrm{E}\left\{n_{a,k}{n}_{a,k}^T\right\}=r_a{I}_3\in R^{3\times 3},\hfill \\ R_g=\mathrm{E}\left\{n_{g,k}{n}_{g,k}^T\right\}=r_g{I}_3\in R^{3\times 3}.\hfill \end{array}$$

(2)

where $r_a>0$ and $r_g>0$ are scalar constants.

We assume that a walking trajectory consists of straight line paths, where the angle between two adjacent paths can only take one of the following angle $\{{90}^{\circ },-{90}^{\circ },{180}^{\circ }\}$. An example of a walking trajectory is given in Figure 1, where there is ${90}^{\circ }$ turn at $P_2$ and $-{90}^{\circ }$ turn at $P_3$. Waypoints are denoted by $P_m\in R^3$ ($1\le m\le M$), which include positions with turn events ($P_2$ and $P_3$ in Figure 1), the initial position ($P_1$) and the final position ($P_4$).

2.1. Standard Inertial Navigation Using an Indirect Kalman Filter

In this subsection, q, r, and v are estimated using a standard inertial navigation algorithm with an indirect Kalman filter [31].

The basic equations for inertial navigation are given as follows:

$$\begin{array}{cc}\dot{q}\hfill & =\frac{1}{2}\Omega \left(\omega \right)q,\hfill \\ {\dot{v}}_n\hfill & =a_n=C^T\left(q\right)a_b,\hfill \\ {\dot{r}}_n\hfill & =v_n,\hfill \end{array}$$

(3)

where symbol $\Omega$ is defined by

$$\Omega \left(\omega \right)=\left[\begin{array}{cc}0& {\omega }^T\\ \omega & -[\omega \times ]\end{array}\right],$$

and $[\omega \times ]\in R^{3\times 3}$ denotes the skew symmetric matrix of $\omega$:

$$[\omega \times ]=\left[\begin{array}{ccc}0& -{\omega }_z& {\omega }_y\\ {\omega }_z& 0& -{\omega }_x\\ -{\omega }_y& {\omega }_x& 0\end{array}\right].$$

Let ${\widehat{q}}_k$, ${\widehat{r}}_k$ and ${\widehat{v}}_k$ be the estimated values of q, r and v using (3), where $\omega$ and $a_b$ are replaced by $y_g$ and $y_a-C\left(\widehat{q}\right)\tilde{g}$:

$$\begin{array}{cc}\dot{\widehat{q}}\hfill & =\frac{1}{2}\Omega \left(y_g\right)\widehat{q},\hfill \\ \dot{\widehat{v}}\hfill & =C^T\left(\widehat{q}\right)y_a-\tilde{g},\hfill \\ \dot{\widehat{r}}\hfill & =\widehat{v}.\hfill \end{array}$$

(4)

Coriolis and Earth curvature effects are ignored since we use a consumer grade IMU for limited walking distances where these effects are below the IMU noise level [32].

When the initial attitude (${\widehat{q}}_0$) is computed, the pitch and roll angles can be computed from $y_{a,0}$. However, the yaw angle is not determined since there is no heading reference sensor such as a magnetic sensor. In the proposed algorithm, the initial yaw angle can be arbitrarily chosen since the yaw angle is automatically adjusted later (see Section 2.3).

${\overline{q}}_e$, $r_e$ and $v_e$ denote the estimation errors in $\widehat{q}$, $\widehat{r}$, and $\widehat{v}$, which are defined by

$$\begin{array}{cc}{\overline{q}}_e\hfill & \triangleq q\otimes {\widehat{q}}_k^{*},\hfill \\ r_e\hfill & \triangleq r_n-{\widehat{r}}_k,\hfill \\ v_e\hfill & \triangleq v_n-{\widehat{v}}_k,\hfill \end{array}$$

(5)

where ⊗ is the quaternion multiplication and $q^{*}$ denotes the quaternion conjugate of a quaternion q. Assuming that ${\overline{q}}_e$ is small, we can approximate ${\overline{q}}_e$ as follows:

$${\overline{q}}_e\approx \left[\begin{array}{c}1\\ q_e\end{array}\right].$$

(6)

The state of an indirect Kalman filter is defined by

$$x\triangleq \left[\begin{array}{c}{q}_e\\ r_e\\ v_e\end{array}\right]\in R^{9\times 1}.$$

(7)

The state equation for the Kalman filter is given by [31]:

$$\dot{x}=\left[\begin{array}{ccc}[-y_g\times ]& 0& 0\\ 0& 0& I_3\\ -2C{\left(\widehat{q}\right)}^T[y_a\times ]& 0& 0\end{array}\right]x+w$$

(8)

where the covariance of the process noise w is given by

$$\mathrm{E}\left\{w{w}^T\right\}=\left[\begin{array}{ccc}0.25R_g& 0& 0\\ 0& 0& 0\\ 0& 0& C{\left(\widehat{q}\right)}^T{R}_{a}C\left(\widehat{q}\right)\end{array}\right].$$

The discretized version of (8) is used in the Kalman filter as in [31].

Two measurement equations are used in the Kalman filter: the zero velocity updating (ZUPT) equation and the map matching equation.

The zero velocity updating uses the fact that there is almost periodic zero velocity intervals (when a foot is on the ground) during walking. If the following conditions are satisfied, the discrete time index k is assumed to belong to zero velocity intervals [31]:

$$\begin{array}{cc}\parallel y_{g,i}\parallel \le B_g,& k-\frac{N_g}{2}\le i\le k+\frac{N_g}{2}\\ \parallel y_{a,i}-y_{a,i-1}\parallel \le B_a,& k-\frac{N_a}{2}\le i\le k+\frac{N_a}{2}\end{array}$$

(9)

where $B_g$, $B_a$, $N_g$ and $N_a$ are parameters for zero velocity interval detection. This zero velocity updating algorithm is not valid when a person is on a moving transportation such as an elevator. Thus, the proposed algorithm cannot be used when a person is on a moving transportation.

During the zero velocity intervals, the following measurement equation is used:

$$0_{3\times 1}-{\widehat{v}}_k=\left[\begin{array}{ccc}{0}_{3\times 3}& 0_{3\times 3}& I_3\end{array}\right]x_k+n_v,$$

(10)

where $n_v$ is a fictitious measurement noise representing a Gaussian white noise with the noise covariance $R_v$.

The second measurement equation is from the map matching, which is used during the zero velocity intervals. From the assumption, a straight line path is parallel to either x axis or y axis. If a path is parallel to $x\left(y\right)$ axis, $y\left(x\right)$ position is constant and this can be used in the measurement equation.

Let $e_i\in R^{3\times 1}(1\le i\le 3)$ be the unit vector whose i-th element is 1 and the remaining elements are 0. Suppose a person is on the path $[P_m,P_{m+1}]$ and

$$\begin{array}{cc}{e}_j^T(P_{m+1}-P_m)=0,& j=1\mathrm{or}2.\end{array}$$

(11)

For example, (11) is satisfied with $j=1$ if the path is parallel to the y axis.

When (11) is satisfied with j ($j=1\mathrm{or}2$), then the map matching measurement equation is given by

$$e_j^T(P_m-{\widehat{r}}_k)=\left[\begin{array}{ccc}{0}_{1\times 3}& e_j^T& 0_{1\times 3}\end{array}\right]x_k+n_{r,12},$$

(12)

where $n_{r,12}$ is the horizontal position measurement noise whose noise covariance is $R_{r,12}$.

If the path is level (that is, $e_3^T(P_{m+1}-P_m)=0$), the z axis value of $r_k$ is almost the same in the zero velocity intervals when the foot is on the ground. In this case, the following z axis measurement equation is also used:

$$e_3^T(P_m-{\widehat{r}}_k)=\left[\begin{array}{ccc}{0}_{1\times 3}& e_3^T& 0_{1\times 3}\end{array}\right]x_k+n_{r,3},$$

(13)

where $n_{r,3}$ is the vertical position measurement noise whose noise covariance is $R_{r,3}$.

The proposed filtering algorithm is illustrated in Figure 2. To further reduce the estimation errors of the Kalman filter, the smoothing algorithm in [31] is applied to the Kalman filter estimated values.

2.2. Path Identification

To apply map matching measurement Equation (12), a current path must be identified. Using the zero velocity intervals, each walking step can be easily determined. Let $S_l$ be the discrete time index of the end of l-th zero velocity interval (see Figure 3).

Let ${\psi }_{S_l}$ be the yaw angle at the discrete time $S_l$ and $△{\psi }_l$ be defined by

$$△{\psi }_l\triangleq {\psi }_{S_{l+1}}-{\psi }_{S_l}.$$

(14)

Please note that $△{\psi }_l$ denotes the yaw angle change during l-th walking step.

The turning (that is, the change of a path) is detected using $△{\psi }_l$. Suppose a current path is $[P_m,P_{m+1}]$. Then the next turning angle is determined by two vectors $P_{m+1}-P_m$ and $P_{m+2}-P_{m+1}$. For example in Figure 1, if a current path is $[P_1,P_2]$, the next turning angle is ${90}^{\circ }$. Let $\delta$ be the next turning angle. Turning is determined to occur at l-th walking step if the following condition is satisfied:

$$\mid \sum _{j=l-M_l}^{l+M_l}△{\psi }_j-\delta \mid <{\psi }_{\mathrm{th}},$$

(15)

where ${\psi }_{\mathrm{th}}$ is a threshold parameter and $M_l$ is a positive integer parameter. Equation (15) detects the turning if the summation of the yaw angle changes during $2M_l+1$ walking steps is similar to the next expected turning angle $\delta$. The use of parameter $M_l$ is due to the fact that turning does not occur during a single step. Once turning is detected in (15), a current path is modified to $[P_{m+1},P_{m+2}]$ from $[P_m,P_{m+1}]$.

2.3. Initial Yaw Angle Adjustment

The initial yaw angle is arbitrarily chosen and adjusted as follows. Suppose the first $N_{\mathrm{first}}$ walking steps belong to the first path $[P_1,P_2]$. Let $x_l$ and $y_l$ ($1\le l\le N_l$) be defined by

$$\begin{array}{cc}\left[\begin{array}{c}{x}_l\\ y_l\end{array}\right]=\left[\begin{array}{c}{e}_1^T\\ e_2^T\end{array}\right]{\widehat{r}}_{S_l},& 1\le l\le N_l.\end{array}$$

(16)

The line equation representing $(x_l,y_l)$ is computed using the following least squares optimization:

$$\underset{a,b,c}{min}\sum _{l=1}^{N_l}{a{x}_l+b{y}_l+c}_2^2.$$

(17)

The angle between the line (defined by the line equation a, b, c) and ${\left[e_1{e}_2\right]}^T(P_2-P_1)$ is computed. Using this angle, the initial yaw angle is adjusted so that the walking direction coincides with the direction dictated by the waypoints.

3. Spline Function Computation

In this section, spline function $\overline{q}\left(t\right)$ (quaternion spline) and $\overline{r}\left(t\right)$ (position spline) are computed using ${\widehat{q}}_k$, ${\widehat{r}}_k$ and ${\widehat{v}}_k$ as control points.

3.1. Cumulative B-Splines Quaternion Curve

Since the quaternion spline $\overline{q}\left(t\right)$ is computed for each interval $[kT,(k+1\left)T\right)$, it is convenient to introduce ${\overline{q}}_k\left(u\right)$ notation, which is defined by

$$\overline{q}\left(t\right)={\overline{q}}_k\left(u\right)\triangleq \overline{q}(kT+u),t\in [kT,(k+1)T),0\le u<T.$$

(18)

To define ${\overline{q}}_k\left(u\right)$, ${\widehat{\omega }}_k$ is defined as follows:

$${\widehat{\omega }}_k\triangleq \frac{1}{T}log\left(C\left({\widehat{q}}_{k+1}\right)C^T\left({\widehat{q}}_k\right)\right),$$

(19)

where the logarithm of an orthogonal matrix is defined in [33]. Please note that ${\widehat{w}}_k$ is a constant angular velocity vector, which transform from ${\widehat{q}}_k$ to ${\widehat{q}}_{k+1}$.

Cumulative B-spline basis function is used to represent the quaternion spline, which is first proposed in [24] and also used in [34].

$${\overline{q}}_k\left(u\right)=(\prod _{i=1}^3{S}_i\left(u\right)){\widehat{q}}_{k-1}$$

(20)

where

$$S_i\left(u\right)\triangleq exp(\frac{1}{2}{\tilde{B}}_i\left(u\right)\Omega ({\widehat{\omega }}_{k-2+i})).$$

The cumulative basis function ${\tilde{B}}_i\left(u\right)\in R^3$ $(1\le i\le 3)$ is defined by

$$\left[\begin{array}{c}{\tilde{B}}_1\left(u\right)\\ {\tilde{B}}_2\left(u\right)\\ {\tilde{B}}_3\left(u\right)\end{array}\right]=D\left[\begin{array}{c}1\\ \frac{u}{T}\\ \frac{u^2}{T^2}\\ \frac{u^3}{T^3}\end{array}\right]$$

(21)

where D is computed using the matrix representation of the De Boor–Cox formula [34]:

$$D=\frac{1}{6}\left[\begin{array}{cccc}5& 3& -3& 1\\ 1& 3& 3& -2\\ 0& 0& 0& 1\end{array}\right].$$

To generate the gyroscope simulation data, the angular velocity spline $\overline{\omega }\left(t\right)$ is required. From the relationship between $\overline{q}\left(t\right)$ and $\overline{\omega }\left(t\right)$ [35], $\overline{\omega }\left(t\right)$ is given by

$$\overline{\omega }\left(t\right)=2\Xi \left(\overline{q}\left(t\right)\right)\dot{\overline{q}}\left(t\right)$$

(22)

where

$$\Xi \left(q\right)\triangleq \left[\begin{array}{ccc}-q_1& -q_2& -q_3\\ q_0& -q_3& q_2\\ q_3& q_0& -q_1\\ -q_2& q_1& q_0\end{array}\right].$$

The derivative of $\overline{q}\left(t\right)$ ($kT\le t<(k+1)T$) is given by

$$\dot{\overline{q}}\left(t\right)=\frac{d{\overline{q}}_k\left(u\right)}{du}=({\dot{S}}_3{S}_2{S}_1+S_3{\dot{S}}_2{S}_1+S_3{S}_2{\dot{S}}_1){\widehat{q}}_{k-1}$$

(23)

where

$${\dot{S}}_i=\frac{d{S}_i\left(u\right)}{du}=\frac{1}{2}{\dot{\tilde{B}}}_i\left(u\right)\Omega \left({\widehat{\omega }}_{k-2+i}\right)S_i$$

$$\dot{\tilde{B}}\left(u\right)=\left[\begin{array}{c}{\dot{\tilde{B}}}_1\left(u\right)\\ {\dot{\tilde{B}}}_2\left(u\right)\\ {\dot{\tilde{B}}}_3\left(u\right)\end{array}\right]=D\left[\begin{array}{c}0\\ \frac{1}{T}\\ \frac{2u}{T^2}\\ \frac{3u^2}{T^3}\end{array}\right].$$

3.2. Eighth-Order Algebraic Splines

The position $\overline{r}\left(t\right)$ is represented by eighth-order algebraic spline [26], where k-th spline segment is given by

$$\overline{r}\left(t\right)={\overline{r}}_{k,m}\left(u\right)=\sum _{j=0}^7{p}_{kj,m}{u}^j,t\in [kT,(k+1)T).$$

(24)

where $p_{kj,m}(0\le k\le N,0\le j\le 7,1\le m\le 3)$ are the coefficients of the k-th spline segment of the m-th element of ${\overline{r}}_k$ (for example, ${\overline{r}}_{k,1}$ is the x position spline). Continuity constraints up to third derivative of ${\overline{r}}_{k,m}\left(u\right)$ are imposed on the coefficients.

Let ${\widehat{a}}_k$ be the estimated value of the external acceleration in the navigation coordinate frame, which can be computed as follows (see (3))

$${\widehat{a}}_k=C^T\left({\widehat{q}}_k\right)y_{a,k}-\tilde{g}.$$

(25)

The coefficients $p_{kj,m}$ are chosen so that $\overline{r}\left(kT\right)$, $\dot{\overline{r}}\left(kT\right)$ and $\ddot{\overline{r}}\left(kT\right)$ are close to ${\widehat{r}}_k$, ${\widehat{v}}_k$ and ${\widehat{a}}_k$. An additional constraint is also imposed to reduce the jerk term (the third derivative of $\overline{r}\left(t\right)$), which makes $\overline{r}\left(t\right)$ smooth rather than jerky. Thus, the performance index for m-th element $(1\le m\le 3)$ of $\overline{r}\left(t\right)$ is defined as follows:

$$\begin{array}{c}{J}_m={\alpha }_1\sum _{k=0}^N{({\overline{r}}_{k,m}\left(T\right)-{\widehat{r}}_{k,m})}^2+{\alpha }_2\sum _{k=0}^N{({\dot{\overline{r}}}_{k,m}\left(T\right)-{\widehat{v}}_{k,m})}^2\hfill \\ +{\alpha }_3\sum _{k=0}^N{({\ddot{\overline{r}}}_{k,m}\left(T\right)-{\widehat{a}}_{k,m})}^2+\beta \sum _{k=0}^N{\int }_0^T{\left({\stackrel{⃛}{\overline{r}}}_{k,m}\left(t\right)\right)}^{2}dt.\hfill \end{array}$$

(26)

This minimization of $J_m$ can be formulated as a quadratic minimization problem of the coefficients $p_{kj,m}$ as follows:

$$\underset{X}{min}{J}_m=X^T{M}_{1}X+2M_{2}X+M_3$$

(27)

where $M_1\in R^{8(N-1)\times 8(N-1)}$, $M_2\in R^{1\times 8(N-1)}$ and $M_3\in R$ can be computed from (26).

Although the matrix size of $M_1$ could be large, it is a banded matrix with a bandwidth of 7. An efficient Cholesky decomposition algorithm is available for matrices with a small bandwidth [36] and (27) can be solved efficiently.

Let ${\overline{p}}_{kj,m}$ be the minimization solution of (26). Then $\overline{r}$ can be computed by inserting ${\overline{p}}_{kj,m}$ into (24) and $\overline{v}$, $\overline{a}$ can be computed by taking the derivatives.

The weighting factors ${\alpha }_i(1\le i\le 3)$ and $\beta$ determine the smoothness of $\overline{r}$, $\overline{v}$ and $\overline{a}$. If $\beta$ is large, we obtain smoother $\overline{r}$, $\overline{v}$ and $\overline{a}$ curves at the sacrifice of nearness to the control points $\widehat{r}$, $\widehat{v}$ and $\widehat{a}$.

Let ${\overline{y}}_a$ and ${\overline{y}}_g$ be accelerometer and gyroscope output generated using the spline functions. These values can be generated using (1), where q, $a_b$, $\omega$ are replaced by $\overline{q}$, $C\left(\overline{q}\right)\overline{a}$, $\overline{\omega }$ with appropriate sensor noises. An overview of the simulation data generation system is shown in Figure 4.

4. Experiment and Results

In this section, the proposed algorithm is implemented through indoor experiments. An inertial measurement unit MTi-1 of XSens was attached on the foot with the sampling frequency of 100 Hz. The parameters used in the proposed algorithm are given in

Table 1. Parameters used in the proposed algorithm

Parameters	Values	Related Equations
$r_a$	0.0015	(2)
$r_g$	0.00001
$B_g$	0.8	(9)
$B_a$	1.5
$N_g,N_a$	30
$n_v$	0.01	(10)
$n_{r,12}$	0.0004	(12)
$n_{r,3}$	0.0004	(13)
${\psi }_{\mathrm{th}}$	${30}^{\circ }$	(15)
${\alpha }_1,{\alpha }_2,{\alpha }_3$	1	(26)
$\beta$	0.00001

.

Two experiment sets of scenarios are conducted: (1) walking along a rectangular path for 2D walking data generation; and (2) walking on corridors and stairs for 3D walking data generation.

4.1. Walking along a Rectangular Path

In this experimental scenario, the subjects walked five laps at normal speed along a rectangular path with dimensions of 13.05 m by 6.15 m. The total distance for five laps on the path was 192 m.

The standard Kalman filter results without map matching are given in Figure 5. The errors in Figure 5 were primarily driven by the errors in the orientation estimation as well as run bias instability of the inertial sensors leading to the position error of 1 m. As can be seen that the maximum error was almost 2 m at the end of the walking.

The navigation results in Figure 6 were obtained from the proposed smoothing algorithm with map matching. It can be seen that the results are improved due to the map matching.

The z axis spline data (for the three walking steps out of the rectangle walking steps) is given in Figure 7.

4.2. Walking along a 3D Indoor Environment

In the second experimental scenario, a person walked along a 3D indoor environment corridors and stairs.

Figure 8 shows the walking along a 3D trajectory results with a waypoint $P_1$ is the starting point whose coordinate is $(0,0,0)$. The coordinates of waypoints $P_1$ to $P_{14}$ are known, and the starting waypoint $P_1$ coincides with the end waypoint $P_{14}$ on the projection plane. The routes are as follow: starting from the third floor waypoint $P_1$, walking along the floor to collect data with normal speed then turning ${180}^{\circ }$ in $P_2$ and turning on the right in $P_3$, then going up the stairs through the floor by the same way as the other floors, finally reaching the fifth floor waypoint $P_{14}$, after that turning ${180}^{\circ }$ and walking along the floor to coming back the starting waypoint $P_1$. The total length of the path line is approximately 562.98 m.

4.3. Evaluation of Simulation Data Usefulness

The simulation data used to test specific performance of a certain algorithm. In this subsection, the standard Kalman filter without map matching is evaluated using the simulation data generated in Section 4.1. The algorithm is tested 1000 times with different noise values (walking motion data is the same).

Let ${\overline{r}}_{xy,\mathrm{final},i}$ be the estimation error of the final position value (x and y components) of i-th simulation, where $1\le i\le 1000$. Since the mean value of ${\overline{r}}_{xy,\mathrm{final},i}$ is not exactly zeros, its mean value is subtracted.

The accuracy of an algorithm can be evaluated from the distribution of ${\overline{r}}_{xy,\mathrm{final},i}$. Consider an ellipse whose center point is the mean of ${\overline{r}}_{xy,\mathrm{final},i}$ and which include 50% of ${\overline{r}}_{xy,\mathrm{final},i}$ (see Figure 9). Let a be the length of the major axis and b be the length of the minor axis. Smaller values of a and b indicate that the error of a certain algorithm is smaller.

4.3.1. Affects of Sampling Rate on the Estimation Performance

The simulation results for the final position estimated errors with different sampling rates are given in

Table 2. Final position errors with different sampling rates.

Sampling Rate	Mean of ${\overline{\mathit{r}}}_{\mathit{xy},\mathbf{final}}$ (m)		Radius (m)
	${\overline{\mathit{x}}}_{\mathbf{final}}$	${\overline{\mathit{y}}}_{\mathbf{final}}$	a	b
50 Hz	−1.5217	−0.5428	0.7605	0.0215
100 Hz	0.6639	0.4745	0.0554	0.0034
150 Hz	0.6955	0.4558	0.0594	0.0032
200 Hz	0.7156	0.4520	0.0582	0.0042

. As an example, Figure 9 shows the estimation error of the final position value with a sampling rate of 100 Hz, where an ellipse represents the boundary of 50% of probability. As can be seen, the final position errors of the different sampling rates are almost the same except for the result with a sampling rate of 50 Hz. This simulation result suggests that the sampling rate is smaller than 100 Hz is not desirable. Also, there is no apparent benefit using the sampling rate higher than 100 Hz.

4.3.2. Gyroscope Bias Effect

The simulation results for the final position estimated errors with different gyroscope bias are given in

Table 3. Final position errors with different gyroscope bias.

${\mathit{r}}_{\mathit{g}}$	Mean of ${\overline{\mathit{r}}}_{\mathit{xy},\mathbf{final}}$ (m)		Radius (m)
	${\overline{\mathit{x}}}_{\mathbf{final}}$	${\overline{\mathit{y}}}_{\mathbf{final}}$	a	b
0	0.7023	0.6122	0.133	0.0226
0.00001	0.6568	0.4696	0.0595	0.0035
0.0001	−0.2038	−0.0280	0.5952	0.0309
0.001	−6.3768	0.5568	3.5123	1.0306

. As can be seen, the final position errors change significantly when the gyroscope bias becomes to change larger.

5. Conclusions

In this paper, simulation data is generated for walking motion estimation using inertial sensors. The first step to generate simulation data is to perform a specific motion, which you want to estimate. The attitude and position are computed from inertial sensors data using a smoothing algorithm. The spline functions are generated using the smoother estimated values as control points. B-spline function is used for the attitude quaternion, and eighth-order algebraic spline function is used for the position.

The spline simulation data generated from the proposed algorithm can be used to test a new motion estimation algorithm by easily changing the parameters such as noise covariance, sampling rate and bias terms.

The shape of generated spline function depends on the weighting factors, which control the constraint on the jerk term. It is one of future research topic to investigate how to choose the optimal weighting factors, which give the most realistic simulation data.