Multi-Sensor Accurate Forklift Location and Tracking Simulation in Industrial Indoor Environments
Abstract
:1. Introduction
1.1. Positioning Systems in Industrial Environments: A Multi-Sensor Approach
- Multipath effectscaused by reflections on metallic materials abundantly found in the infrastructure, machinery, forklifts, tools, raw material, etc. Hence, RF-based location technologies will experience a significant performance degradation in these scenarios due to rich multipath wireless channels.
- Obstacles in an industrial environment are typically produced by the movement of people and objects, yielding a phenomena known as shadowing, which hinders the visibility of the location target.
- Operational continuity of the location process in an industrial scenario (or in a generic workplace) in the sense of producing the minimum impact on existing workflow and protocols.
- Strength: each technology has different weak points. A combination of technologies can help to overcome this problem because not all of them are going to fail simultaneously.
- Flexibility: future requirements or problems can be solved or mitigated by incorporating additional sensors.
- Granularity: Typically, different requirements are identified depending on the area or zone inside a building or warehouse. A multi-technology approach addresses better this situation by using a different set of sensors (varying its number and type) according to the needs imposed by each area.
- Cost: a higher number of technologies allows for selecting the sensors and their development tools and platforms from a larger set, thus easing the problem of finding an alternative that fits the budget.
1.2. The Proposed Solution: Multi-Sensor Forklift Location and Tracking
- The number of forklifts is orders of magnitude lower than the number of pallets, hence reducing the deployment cost.
- Maintenance costs are also lower. These costs can be crucial in the long term since the difference between maintaining only a few units in the face of hundreds or thousands is very significant.
- Different technologies can be used to perform the two above-mentioned pallet-positioning steps, and the system could be improved in the future by adding new ones.
- Forklift tracking provides value-added information and companies can exploit it profitably (e.g., route optimization and safety).
1.3. Main Contributions
- A UWB simulator capable of replicating in Gazebo the behavior of this technology when used for a real-world location. Unlike other more focused approaches in replicating the radio signal at low level [20], the solution implemented in this work models the high level behavior of the range and received signal strength (RSS) values produced by this type of devices.
- A model of a vehicle (the forklift) with the motion model of this type and machines and taking into account the placement of the considered sensors on the forklift.
- A location algorithm based on Kalman filter designed to merge all the data coming from the sensors. Such a location algorithm is implemented using the robot operating system (ROS) ecosystem [21], an open source framework for writing robot software.
- The simulated vehicle (a forklift in our case) has exactly the same elements (sensors, processors, etc.) as those a real vehicle would equip.
- The location algorithm does not have to be re-implemented for the simulator. Instead, the same code that will run in the hardware is used by the simulator. In this case, the location algorithm is implemented in ROS, a well known and widely used technology.
- Multiple location algorithm implementations can be tested under the same conditions without requiring costly and time-consuming measurement campaigns.
- Additional sensors can be included in the considered sensor set to evaluate their impact on the performance of the location algorithms. Although validating the models for these new sensors might require measurements, they will not involve the whole system.
- More scenarios and vehicles can be included in the simulator to assess more complex environments.
2. Sensor Considered for Industrial Environments
- Precision up to 10 cm.
- High data rate communications, up to 6.8 byte/s.
- Highly immune to multi-path fading.
- Low power consumption.
3. UWB Simulator
- LOS: in this situation there were no obstacles between the tag and the anchor. With this configuration, the distance estimate provided by the devices was very close to the actual distance between them.
- NLOS soft: in this situation there was an obstacle between the tag and the anchor. Despite this, the devices were able to decode the correct path, hence the distance estimate was also close to the real value. However, as a result of the attenuation caused by the obstacle, the received power level was significantly lower than that in the LOS case.
- NLOS hard: in this situation there was an obstacle that totally blocked the direct line of sight between the tag and the anchor. Unlike in the NLOS soft case, the first direct path of the signal was totally blocked, hence one of the delayed paths (corresponding to signal rebounds) was decoded instead. In this case, and because the time of flight (TOF) of the signal was considerably greater than the minimum distance, the estimate provided by the UWB devices was always greater than the actual distance. In this situation, measurements were obtained with several centimeters of error, exceeding the meter in some cases.
- The tag modeled with the plug-in searches the stage for the elements marked as UWB anchors.
- For each anchor, the plug-in uses ray tracing to check if there is a direct line of sight with the tag. Then, if the power estimate is high enough, the range is considered as belonging to the LOS scenario, hence a measurement corresponding to the distance between them is generated (after applying the offset correction factor).
- If there is an obstacle between the tag and the anchor, the thickness of the element (i.e., obstacle attenuation) is checked. If its value is below a threshold (configurable in the plug-in), then it is considered that the first path of the signal is able to pass through it. Therefore, the NLOS soft configuration is applied and the ranging value is generated. Again, if the estimated power is below the threshold, then the ranging value would not be generated.
- If there is an obstacle between the tag and the anchor, but its thickness exceeds the level established to be considered NLOS soft, we proceed to start a search for possible bounces. In this case, and in order to keep the computational cost reduced, ray tracing is employed to look for bounces in obstacles located at the same height as the tag (i.e., walls), but not in floors or ceilings. In addition, the search is limited to a single bounce before reaching the target. In case that after this rebound there is a path free of obstacles between the tag and the anchor, it is established that the scenario corresponds to NLOS hard and both ranging and received power estimates are generated. As in the previous cases, if the received power estimate is below the threshold, the acquired information is discarded, including the ranging estimates.
Simulation Accuracy
4. Location Algorithm
4.1. Forklift Motion Model
- move only in two dimensions (on a plane over the ground).
- move forward and backward.
- move tracing a curve or in a straight line.
- spin around its Z axis without performing a displacement in X and Y axes.
4.2. Location Algorithm Design
5. Software Implementation
5.1. ROS Nodes
- The UWB plug-in (gtec_uwb_plugin, see Table 1) publishes in the ROS ecosystem the messages corresponding to the position of the anchors in the scenario and the ranging values with respect to the tag associated to the plug-in.
- The gtec_tag_pos_publisher_plugin plug-in (see Table 2) publishes the true position of the object to which it is attached. Such position values consists of the x, y, and z coordinates together with the quaternion and they are used to plot the actual trajectories followed by the object.
- The gazebo2ros node (see Table 3) acts as relay to capture the measurements of different sensors in Gazebo and publish them through ROS. More specifically, in this work it is used to publish the data from the inertial measurement unit (IMU) and the PX4 Flow sensors.
- The kfpos node (see Table 4) contains the implementation of the positioning algorithm described in Section 4, it has subscriptions to several topics (to receive data from the different sensors), and publishes the position estimation on another topic. In this specific implementation of the IEKF, the following parameters were used:
- -
- Maximum number of iterations: 50.
- -
- Minimum cost goal: .
- -
- Maximum Jolt: m/s.
- The gazebo2rviz node [46] plots in the application RVIZ the position of the static elements (e.g., walls) placed in the Gazebo simulation.
- The turtlebot3_gazebo node [47] is used as a base to model the forklift vehicle.
- The teleop_twist_joy node [48] modifies the angular and linear speed of the vehicle through a USB joystick to easily move the simulated forklift across the different scenarios. To reproduce the routes, the messages of this node are recorded in a log that can be replayed later on.
- The mavros_extras node [49], which includes the definition of the message type OpticalFlowRad used to represent the output of the PX4 Flow sensor.
- The Flow_Plugin plug-in included in the PX4 Autopilot Firmware [50], which is employed to create the PX4 Flow sensor in Gazebo.
5.2. ROS Custom Messages
- anchorId: anchor identifier.
- tagId: tag identifier.
- range: distance value expressed in millimeters.
- seq: sequence number. Several ranging measurements can have the same sequence number if they were created at the same time.
- errorEstimation: error estimate within the provided range value.
- rss: received power estimate.
6. Software Simulation
6.1. Gazebo Physics Simulator
- A set of physics engines. Gazebo supports different physics engines such as ODE, Bullet, Simbody, or DART. They allow for simulating different physical processes such as movement, collisions, and falls.
- The OGRE 3D render engine, allowing for creating realistic 3D object models and worlds.
- Several sensor models, such as optical or motion ones, supporting noise addition to the sensor data following different models.
- A plug-in system allowing for creating new functionality and extend its base behavior, including the creation of new sensor types or new environment characteristics.
6.2. Simulation Elements
6.2.1. Simulated Scenarios
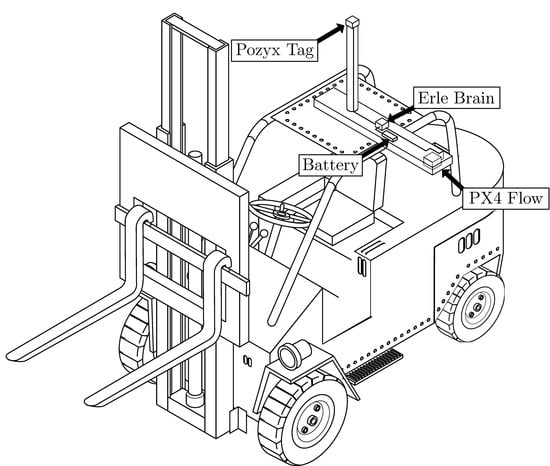
6.2.2. Simulated Vehicle and Sensors
- Angular type: Gaussian.
- Angular .
- Angular .
- Angular bias .
- Angular bias .
- Linear type: Gaussian.
- Linear .
- Linear .
- Linear bias .
- Linear bias .
- Type: Gaussian.
- .
- = .
6.3. Simulation Methodology and Figures of Merit
7. Results
- NLOS soft situation: the direct path can be decoded and hence the positioning algorithm provides estimates close to the true values.
- There was no link between the anchor and the tag, neither the direct path nor a rebound. In this situation, no ranging value wasgenerated and therefore had no influence on the algorithm.
- NLOS hard situation: the direct path was blocked, but a signal rebound enabled a wireless link between the anchor and the tag, although severely degrading the provided ranging estimate, hence strongly penalizing the localization algorithm.
8. Conclusions and Future Lines
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ECDF | empirical cumulative distribution function |
| IC | integrated circuit |
| IEKF | iterated extended Kalman filter |
| IMU | inertial measurement unit |
| LOS | line-of-sight |
| MAE | mean absolute error |
| MMSE | minimum mean square error |
| NN | neural network |
| NLOS | non-line-of-sight |
| RF | radio frequency |
| ROS | robot operating system |
| RSS | received signal strength |
| RTLS | real-time location system |
| TOF | time of flight |
| TOA | time of arrival |
| TDOA | time-difference of arrival |
| UKF | unscented Kalman filter |
| UWB | ultra-wideband |
References
- Mautz, R. Indoor Positioning Technologies. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2012. [Google Scholar]
- Lasi, H.; Fettke, P.; Kemper, H.G.; Feld, T.; Hoffmann, M. Industry 4.0. Bus. Inf. Syst. Eng. 2014, 6, 239–242. [Google Scholar] [CrossRef]
- Farid, Z.; Nordin, R.; Ismail, M. Recent advances in wireless indoor localization techniques and system. J. Comput. Networks Commun. 2013, 2013. [Google Scholar] [CrossRef]
- Lopez-Iturri, P.; Led, S.; Aguirre, E.; Azpilicueta, L.; Serrano, L.; Falcone, F. Analysis of Bluetooth-Based Wireless Sensor Networks Performance in Hospital Environments. Proceedings 2017, 1. [Google Scholar] [CrossRef]
- Aguirre, E.; Lopez-Iturri, P.; Azpilicueta, L.; Astrain, J.J.; Villadangos, J.; Santesteban, D.; Falcone, F. Implementation and Analysis of a Wireless Sensor Network-Based Pet Location Monitoring System for Domestic Scenarios. Sensors 2016, 16, 1384. [Google Scholar] [CrossRef] [PubMed]
- Duvallet, F.; Tews, A.D. WiFi position estimation in industrial environments using Gaussian processes. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Nice, France, 22–26 September 2008; pp. 2216–2221. [Google Scholar]
- García, E.; Poudereux, P.; Hernández, Á.; Ureña, J.; Gualda, D. A robust UWB indoor positioning system for highly complex environments. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 3386–3391. [Google Scholar]
- Kok, M.; Hol, J.D.; Schön, T.B. Indoor positioning using ultrawideband and inertial measurements. IEEE Trans. Veh. Technol. 2015, 64, 1293–1303. [Google Scholar] [CrossRef]
- Tiemann, J.; Schweikowski, F.; Wietfeld, C. Design of an UWB indoor-positioning system for UAV navigation in GNSS-denied environments. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015; pp. 1–7. [Google Scholar]
- Alsindi, N.A.; Alavi, B.; Pahlavan, K. Measurement and modeling of ultrawideband TOA-based ranging in indoor multipath environments. IEEE Trans. Veh. Technol. 2009, 58, 1046–1058. [Google Scholar] [CrossRef]
- Lee, J.Y.; Scholtz, R.A. Ranging in a dense multipath environment using an UWB radio link. IEEE J. Sel. Areas Commun. 2002, 20, 1677–1683. [Google Scholar]
- Pahlavan, K.; Krishnamurthy, P.; Beneat, A. Wideband radio propagation modeling for indoor geolocation applications. IEEE Commun. Mag. 1998, 36, 60–65. [Google Scholar] [CrossRef] [Green Version]
- Pahlavan, K.; Akgul, F.O.; Heidari, M.; Hatami, A.; Elwell, J.M.; Tingley, R.D. Indoor geolocation in the absence of direct path. IEEE Wirel. Commun. 2006, 13, 50–58. [Google Scholar] [CrossRef]
- Xiao, W.; Ni, W.; Toh, Y.K. Integrated Wi-Fi fingerprinting and inertial sensing for indoor positioning. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN 2011), Guimaraes, Portugal, 21–23 September 2011; pp. 1–6. [Google Scholar]
- Corrales, J.A.; Candelas, F.; Torres, F. Hybrid tracking of human operators using IMU/UWB data fusion by a Kalman filter. In Proceedings of the 3rd ACM/IEEE International Conference on Human-Robot Interaction (HRI), Amsterdam, The Netherlands, 12–15 March 2008; pp. 193–200. [Google Scholar]
- Solutions, V. Vero Solutions. 2019. Available online: https://vero.solutions/warehouse-real-time-location-systems/ (accessed on 9 October 2019).
- Solutions, T. Tech Solutions. 2019. Available online: https://www.techsolutions.co.za/rfid-pallet-tracking/ (accessed on 9 October 2019).
- Path, T. Touch Path. 2019. Available online: https://touchpath.com/ (accessed on 9 October 2019).
- Gazebo. Gazebo Simulator. 2019. Available online: http://gazebosim.org (accessed on 9 October 2019).
- Vial, P.J.; Wysocki, B.J.; Wysocki, T.A. An Ultra Wide Band Simulator Using MATLAB/Simulink. In Proceedings of the 8th International Symposium on DSP and Communication Systems DSPCS’2005, Sunshine Coast, Australia, 19–21 December 2005; pp. 231–236. [Google Scholar]
- ROS. ROS. 2019. Available online: http://http://www.ros.org (accessed on 9 October 2019).
- Barral, V. Rosuwbreader. 2019. Available online: https://github.com/valentinbarral/rosuwbreader (accessed on 9 October 2019).
- Barral, V. Rostoa. 2019. Available online: https://github.com/valentinbarral/rostoa (accessed on 9 October 2019).
- Barral, V. Rosmsgs. 2019. Available online: https://github.com/valentinbarral/rosmsgs (accessed on 9 October 2019).
- Barral, V. Roslogscripts. 2019. Available online: https://github.com/valentinbarral/roslogscripts (accessed on 9 October 2019).
- Barral, V. Roskfpos. 2019. Available online: https://github.com/valentinbarral/roskfpos (accessed on 9 October 2019).
- Barral, V. Gazebosensorplugins. 2019. Available online: https://github.com/valentinbarral/gazebosensorplugins (accessed on 9 October 2019).
- Barral, V. Gazeboforkliftsimulation. 2019. Available online: https://github.com/valentinbarral/gazeboforkliftsimulation (accessed on 9 October 2019).
- Barral, V. Gazebo2ros. 2019. Available online: https://github.com/valentinbarral/gazebo2ros (accessed on 9 October 2019).
- Caso, G.; Le, M.; De Nardis, L.; Di Benedetto, M.G. Performance Comparison of WiFi and UWB Fingerprinting Indoor Positioning Systems. Technologies 2018, 6, 14. [Google Scholar] [CrossRef]
- Decawave. Decawave DW1000. 2019. Available online: https://www.decawave.com/products/dw1000 (accessed on 9 October 2019).
- Pozyx. Pozyx. 2019. Available online: https://www.pozyx.io (accessed on 9 October 2019).
- Barral, V.; Suárez-Casal, P.; Escudero, C.J.; García-Naya, J.A. Assessment of UWB Ranging Bias in Multipath Environments. In Proceedings of the 7th International Conference on Indoor Positioning and Indoor Navigation (IPIN), Madrid, Spain, 4–7 October 2016; pp. 1–4. [Google Scholar]
- Silva, B.; Pang, Z.; Åkerberg, J.; Neander, J.; Hancke, G. Experimental study of UWB-based high precision localization for industrial applications. In Proceedings of the 2014 IEEE International Conference on Ultra-WideBand (ICUWB), Paris, France, 1–3 September 2014; pp. 280–285. [Google Scholar]
- Hancke, G.P.; Allen, B. Ultrawideband as an industrial wireless solution. IEEE Pervasive Comput. 2006, 5, 78–85. [Google Scholar] [CrossRef]
- Honegger, D.; Meier, L.; Tanskanen, P.; Pollefeys, M. An open source and open hardware embedded metric optical flow CMOS camera for indoor and outdoor applications. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 1736–1741. [Google Scholar]
- Gazebo. Gazebo Building Editor. 2019. Available online: http://gazebosim.org/blog/buildingeditor (accessed on 9 October 2019).
- Barral, V.; Escudero, C.; García-Naya, J. NLOS Identification and Mitigation Using Low-Cost UWB Devices. IEEE Dataport 2019. [Google Scholar] [CrossRef]
- Barral, V.; Escudero, C.; García-Naya, J.; Maneiro-Catoira, R. NLOS Identification and Mitigation Using Low-Cost UWB Devices. Sensors 2019, 19, 3464. [Google Scholar] [CrossRef] [PubMed]
- Venkatesh, S.; Buehrer, R.M. Non-line-of-sight identification in ultra-wideband systems based on received signal statistics. IET Microw. Antennas Propag. 2007, 1, 1120–1130. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Peipei, C.; Xinwei, Z.; Qinyu, Z.; Naitong, Z. Characterization of indoor ultra-wide band NLOS channel. In Proceedings of the IEEE Annual Wireless and Microwave Technology Conference, Clearwater Beach, FL, USA, 4–5 December 2006; pp. 1–5. [Google Scholar]
- Barral, V.; Escudero, C.J.; García-Naya, J.A. NLOS Classification Based on RSS and Ranging Statistics Obtained from Low-Cost UWB Devices. In Proceedings of the 27th European Signal Processing Conference (EUSIPCO), A Coruña, Spain, 2–6 September 2019. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the Neural Information Processing Systems Conference (NIPS 2012), Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar]
- Decawave. Decawave DW1000 IC. 2019. Available online: https://www.decawave.com/product/dw1000-radio-ic/ (accessed on 9 October 2019).
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974. [Google Scholar]
- ROS. Gazebo2rviz ROS Node. 2019. Available online: http://wiki.ros.org/gazebo2rviz (accessed on 9 October 2019).
- ROS. Turtlebot3_gazebo ROS Node. 2019. Available online: http://wiki.ros.org/turtlebot3_gazebo (accessed on 9 October 2019).
- ROS. Teleop_twist_joy ROS Node. 2019. Available online: http://wiki.ros.org/teleop_twist_joy (accessed on 9 October 2019).
- ROS. Mavros ROS Package. 2019. Available online: http://wiki.ros.org/mavros (accessed on 9 October 2019).
- PX4. PX4 Autopilot Firmware. 2019. Available online: https://github.com/PX4/Firmware (accessed on 9 October 2019).















| Topic | Message Type | Topic Type |
|---|---|---|
| /gtec/gazebo/uwb/ranging/id | gtec_msgs::Ranging | Published |
| /gtec/gazebo/uwb/anchors/id | visualization_msgs::MarkerArray | Published |
| Topic | Message Type | Topic Type |
|---|---|---|
| /gtec/gazebo/pos | geometry_msgs::PoseWithCovarianceStamped | Published |
| Topic | Message Type | Topic Type |
|---|---|---|
| /gtec/gazebo/imu | sensor_msgs::Imu | Published |
| /gtec/gazebo/PX4 Flow | mavros_msgs::OpticalFlowRad | Published |
| Topic | Message Type | Topic Type |
|---|---|---|
| /gtec/gazebo/uwb/ranging/id | gtec_msgs:: Ranging | Subscription |
| /gtec/gazebo/PX4 Flow | mavros_msgs::OpticalFlowRad | Subscription |
| /gtec/gazebo/imu | sensor_msgs:: Imu | Subscription |
| /gtec/kfpos | geometry_msgs:: PoseWithCovarianceStamped | Published |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barral, V.; Suárez-Casal, P.; Escudero, C.J.; García-Naya, J.A. Multi-Sensor Accurate Forklift Location and Tracking Simulation in Industrial Indoor Environments. Electronics 2019, 8, 1152. https://doi.org/10.3390/electronics8101152
Barral V, Suárez-Casal P, Escudero CJ, García-Naya JA. Multi-Sensor Accurate Forklift Location and Tracking Simulation in Industrial Indoor Environments. Electronics. 2019; 8(10):1152. https://doi.org/10.3390/electronics8101152
Chicago/Turabian StyleBarral, Valentín, Pedro Suárez-Casal, Carlos J. Escudero, and José A. García-Naya. 2019. "Multi-Sensor Accurate Forklift Location and Tracking Simulation in Industrial Indoor Environments" Electronics 8, no. 10: 1152. https://doi.org/10.3390/electronics8101152
APA StyleBarral, V., Suárez-Casal, P., Escudero, C. J., & García-Naya, J. A. (2019). Multi-Sensor Accurate Forklift Location and Tracking Simulation in Industrial Indoor Environments. Electronics, 8(10), 1152. https://doi.org/10.3390/electronics8101152