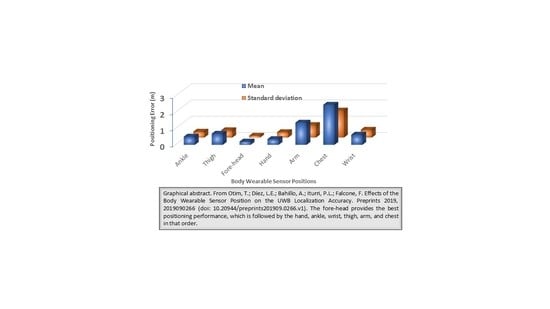
Effects of the Body Wearable Sensor Position on the UWB Localization Accuracy

Abstract

Over the years, several Ultrawideband (UWB) localization systems have been proposed and evaluated for accurate estimation of the position for pedestrians. However, most of them are evaluated for a particular wearable sensor position; hence, the accuracy obtained is subject to a given wearable sensor position. This paper is focused on studying the effects of body wearable sensor positions i.e., chest, arm, ankle, wrist, thigh, forehead, and hand, on the localization accuracy. According to our results, the forehead and the chest provide the best and worst body sensor location for tracking a pedestrian, respectively. With the wearable sensor at the forehead and chest position, errors lower than 0.35 m (90th percentile) and 4 m can be obtained, respectively. The reason for such a contrast in the performance lies in the fact that, in non-line-of-sight (NLOS) situations, the chest generates the highest multipath of any part of the human body. Thus, the large errors obtained arise due to the signal arriving at the target wearable sensor by multiple reflections from interacting objects in the environment rather than by direct line-of-sight (LOS) or creeping wave propagation mechanism.

1. Introduction

Wearable technology holds a great deal of promise: by 2025, its market is expected to reach $70 billion [1]. Wearables are capable of delivering exceptional opportunities for dealing with societal challenges. This can be achieved by providing solutions in areas of patient monitoring [2], healthy ageing [3], safety at work [4], emergency management [5], and others. Therefore, major sectors in this market are expected to remain as consumer electronics, defence, and healthcare. Usually, the market sector that the wearable aims to address often determines its position on the body. For instance, in emerging opportunities for localization and tracking, wearables can be positioned at the ankle, head, and wrist for monitoring of inmates in prisons, miners trapped in mines, and patients inside hospitals, respectively [6]. Nowadays, one of the key and most relevant applications of wearables is in localization systems [7,8,9]. In fact, wearables can now include, for instance: (i) inertial sensors for measuring the angular velocity and linear acceleration [10]; (ii) magnetometer for measuring the heading [11]; and (iii) proximity sensors for detecting if a defined subject or obstacle is present nearby [12].

Estimation of the position of a target in an outdoor environment is performed using Global Navigation Satellite Systems (GNSS) such as Global Positioning Systems (GPS). However, in indoor environments, GNSS cannot work properly because of the weak satellite signals [13]. For this reason, research efforts in the field of positioning have been directed towards indoor scenarios with an aim of establishing a standard indoor positioning system (IPS) that can be applied worldwide.

Globally, the most widespread category of indoor positioning technologies are beacon based. These use pre-installed infrastructure at known locations to estimate the position of a moving object by measuring the angle of arrival [14], time of flight (TOF) [15], or received signal strength measurements [16]. Nonetheless, because of pathloss, multipath fading, and human body shadowing challenges, the ranging and positioning accuracy of these localization techniques is decreased. This is why indoor localization of pedestrians and objects is still an open problem. The current state of the art tries to solve these problems using advanced processing techniques, such as Kalman Filters [17,18,19] and Particle Filters [20,21,22]. However, these techniques still neglect the effect of human body shadowing.

Among the beacon-based localization solutions, the most accurate are those that use ultrasound or UWB signals [23]. Thus, UWB technology has gathered a great interest in academic and industry research because of a confluence of factors such as decimeter-level location estimates, low-cost implementation, immunity to fading, and low-power transmission. In fact, according to Apple [24], the new iPhone 11 already includes an UWB interface and UWB beacons are expected to be released soon. This demonstrates the attractiveness of this technology.

Over the years, UWB has been used for ranging and positioning [25,26,27], but its performance deteriorates in non-line-of sight (NLOS) situations. In tracking context of pedestrians using UWB technology, an important factor which has often been overlooked but has significant effect on the ranging and positioning error is the influence caused by the human body itself in NLOS situations. Additional propagation losses or biases in TOF measurements are the after-effects of human body shadowing, and they depend on: (i) body wearable sensor position; and (ii) relative heading angle (RHA). Therefore, in this work, we study how the different body wearable positions contribute towards human body shadowing by analyzing their effects on the UWB localization accuracy.

This paper is organized as follows. Section 2 presents related works on the effect of wearable sensor positions on either UWB ranging or positioning accuracy. Section 3 describes UWB interaction with the human body. The measurement setup and methodology adopted is described in Section 4. The UWB ranging and positioning performance is investigated in Section 5 and Section 6 for different body wearable sensor positions. In Section 7, the presentation and discussion of results is made. Finally, in Section 8, concluding remarks are drawn and future work is discussed.

2. Related Work

Currently, studies available on the impact of human body on the ranging and positioning error are performed for a particular body wearable position. Additionally, these studies are performed in a static context with discrete RHAs, i.e., angles between the direction in which the pedestrian is facing and the direction of the receiver-transmitter line. For instance, in [28], the authors developed a human body shadowing identification and error mitigation technique for emergency responders. In this work, the wearable sensor is placed on the waist of the body. Tian et al. [29] studied the effect of human body shadowing on the ranging and positioning results, however, the results are only for a handheld sensor. Jie He et al. [30] analyzed the TOF ranging error along a straight corridor, but for wearables mounted on the chest and wrist positions. Although Bharadwaj and Koul [31] empirically analyzed a body to body UWB communication channel for different body wearable positions, they did not consider the positioning application. Other approaches to study the effect of the human body on the ranging error are simulations, such as the works of Otim et al. [32] and Yishuang Geng et al. [33] for sensors mounted on the hand and chest positions, respectively. Others (e.g., [34,35,36]) do not consider a body wearable position, but a human body as an obstacle standing between a tripod mounted with a wearable sensor and the anchor.

To overcome the drawbacks of human body shadowing on the TOF positioning error, ranging models that consider the body shadowing effect are necessary. Thus, in [37], we developed ranging error models for different body wearable sensor positions such as the forehead, hand, chest, wrist, arm, thigh and ankle. Other ranging error models are also presented for the hand [29,32], for the wrist and chest [30,38,39], and for the waist position [28].

Based on the related work, there is no work in the literature that studies the effects of wearable positions on the positioning accuracy. Therefore, this paper is an extension of the work in [37], in which novel UWB ranging error models for different wearable positions are proposed. We performed experiments considering seven locations: hand, chest, arm, thigh, forehead, ankle, and wrist. Additionally, the localization performance for the considered body positions was analyzed using an Extended Kalman Filter (EKF) because it takes advantage of the dynamic context of the user, i.e., it is tailor-made for tracking mobile objects.

3. UWB Interaction with the Human Body

UWB has the ability to measure the TOF with high resolution, and therefore to accurately estimate ranges in LOS conditions. However, when the direct path is blocked by the human body, the NLOS effect creates longer paths, which correspond to significant errors from a few decimeters to several meters based on the body wearable sensor position [37]. In this section, we describe how the body regions thorax, limb, and head influence the ranging error in NLOS situations.

Ideally, when electromagnetic waves interact with the body, part of the signal is reflected, refracted, diffracted, and the other part is transmitted through the body. Given that the body is composed of various organs with different tissue types (see

Table 1. Tissue thickness in millimeters for different body regions [42,43]. Note that tissues which are only specific to a body region, such as lungs and heart for the thorax, as well as brain and cerebrospinal fluids for the head, have not been included.

Tissue	Thorax	Limbs	Head
Skin	1.4–2.6	0.6–2.0	0.5–2
Fat	0.6–15.0	0.4–20.6	1–2
Muscle	0.0–30.0	0.0–3.0	0–4
Bone	5.6–6.6	-	1–10

), several electrical characteristics such as relative permittivity, power absorption, conductivity, and path loss are vastly inhomogeneous [40,41]. It is also apparent in Table 1 that these tissues also vary in thickness.

A pulse that is sent towards a target sensor at a given body region (position) will cross several layers, generating attenuation and delay due to the impedance mismatch between adjacent tissues. The additional range error is often proportional to the tissues’ relative permittivity and thickness, and can be as important as the range error created by any other obstacle in the environment. In fact, by taking into consideration that the speed of the waves in the body is dependent on the permittivity and the conductivity of the tissue, range error is from 0.2 to 0.5 m since RF propagation through the body takes between 0.7 and 1.6 ns [41,42]. However, the aforementioned range errors are likely to change because UWB propagation between the wearable sensor and anchors can involve a combination of the following propagation mechanisms that are critical for any robust localization system: LOS, refractions, creeping wave, diffractions, and multiple reflections.

As stated above, mathematical models are often used to successfully mitigate or reduce the range error. In [37], we modeled the probability distribution function (PDF) of the ranging error for different body wearable positions taking into consideration human body shadowing situations. For instance, due to the circular shape of the head, this body position body suffers less NLOS situations, so the Gaussian distribution in Equation (1) is sufficient to model both LOS and NLOS errors. In Equation (1), $ϵ$ is the range error, $\mu$ is the mean range error, and $\sigma$ is the standard deviation (SD).

$$f\left(ϵ\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{(ϵ-\mu )}^2}{2{\sigma }^2}}$$

(1)

For the wearables located at the chest and hand, the range errors can be modeled as the sum of a Gaussian and a Gamma PDF, as shown in Equation (2), for errors obtained in LOS and NLOS, respectively. The LOS and NLOS situations change depending on the RHA between the pedestrian and the anchor.

$$f\left(ϵ\right)=\delta \left(RHA\right).\left(\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{(ϵ-\mu )}^2}{2{\sigma }^2}}\right)+(1-\delta \left(RHA\right)).\left(\lambda .e^{-\lambda ϵ}.\frac{{\left(\lambda ϵ\right)}^{k-1}}{\mathsf{\Gamma }\left(k\right)}+c\right)$$

(2)

The $\delta \left(RHA\right)$ is a unit impulse function described in Equation (3) as:

$$\delta \left(RHA\right)=\left\{\begin{array}{cc}0,\hfill & RHA\in [0°,112.5°)\bigcup (247.5°,360°]\hfill \\ 1,\hfill & RHA\in [112.5°,247.5°]\hfill \end{array}\right.$$

(3)

Finally, when the wearable sensor is located on the limbs such as the wrist, arm, ankle, and thigh, the range error is modeled by a Gamma distribution both in LOS and NLOS conditions, as shown by the PDF in Equation (4).

$$f\left(ϵ\right)=\delta \left(RHA\right).\left(b.e^{-bϵ}.\frac{{\left(bϵ\right)}^{a-1}}{\mathsf{\Gamma }\left(a\right)}\right)+(1-\delta \left(RHA\right)).\left(\lambda .e^{-\lambda ϵ}.\frac{{\left(\lambda ϵ\right)}^{k-1}}{\mathsf{\Gamma }\left(k\right)}\right)+c$$

(4)

4. Experimental Setup

To illustrate the the effects of the wearable sensor positions on the ranging and localization accuracy, experiments were conducted with TREK1000 development kits manufactured by Decawave. These are the best off-the-shelf products available for UWB ranging [23,44]. The transceiver used in the measurements is DW1000 802.15.4a IR-UWB, and is able to achieve two-way ranging between a wearable sensor and all the anchors with an update rate of 3.57 Hz [45]. Using the dip switches, we were able to select the data rate of 110 kb/s and a central frequency of 3990 MHz.

The measurement campaign was performed at the Luis Mercader Lab, department of Electric, Electronic and Communication engineering at the Public University of Navarra in Spain (see Figure 1). The Lab covered an area of 78 m${}^2$. Inside of the Lab were computers, closets and chairs, which contributed in creating different propagation mechanisms among the UWB signals.

A floor plan of the Lab is illustrated in Figure 2. It shows a path with 26 ground-truth points and detailed anchor positions. The top left corner was considered as the origin of our reference system. The X–Y positions for the anchors and ground-truth points were obtained using a laser rangefinder. During the measurements, one transceiver node was configured as a wearable sensor and four others as anchors. Each anchor was placed on a tripod and their positions are shown in

Table 2. Coordinates of UWB Anchors.

Anchor	X (cm)	Y (cm)	Z (cm)
Anchor 0	1240	571	170
Anchor 1	1240	70	173
Anchor 2	548	33	172
Anchor 3	68	21	172

.

The experimentation consisted of moving one mobile wearable sensor to 26 different ground-truth positions. Using the installed ground-truth points, firstly, the wearable sensor was mounted on a tripod at a height of 177 cm and moved along the path starting from ground-truth point 1 and ending at ground-truth point 26 (see Figure 2) as a reference for further comparisons.

In the second campaign, a male subject with 77 kg mass and 1.80 m height was considered. On the subject, the sensors were placed on the forehead, right arm, right ankle, chest, right wrist, right thigh, and right hand with the help of velcro straps, as shown in Figure 3. The heights at which the wearable sensors were mounted are shown in

Table 3. Height (H) in centimeters at which the wearable sensors are mounted.

	Ankle	Thigh	Forehead	Hand	Arm	Chest	Wrist
H	15	70	177	120	130	130	90

.

Then, for each wearable sensor position, the subject was made to walk the same path following two scenarios (discrete and continuous). In the discrete scenario, the measurements were recorded manually for 30 s only when the subject transitioned to the correct ground-truth point.

Similar to the work in [44], in the continuous scenario, the ranges were recorded continuously without stopping as the subject moved from the start to end. At each ground-truth point, the subject stood still for approximately 10 s before moving to the next. We repeated the experiment by each body sensor location (seven times) aiming at minimizing any possible interference that could arise among the sensors.

5. Analysis of the Ranging Performance

Based on the measured TOF and the speed of radio wave propagation, the distance between the wearable sensor and the anchors can be determined. Therefore, using the test setup described above, we computed the range by measuring the two-way TOF between the wearable sensor and the anchors, and using the speed of light as the speed of the radio waves.

In Figure 4 and Figure 5, we show the measured error computed as the measured distance minus the true distance. Since the time spent at a single ground-truth position was 30 s, the respective mean average error (MAE) was generated from at least 100 distance readings. Note that, in analyzing the ranging performance, only the ranges from the discrete scenario were used.

In Figure 4, we show the measurements taken when the wearable sensor was placed on the tripod, without human body presence, i.e., the ranging errors obtained in an almost ideal LOS situation. We can appreciate in this figure that the UWB range errors are decimeter level. In fact, we computed a mean error of 11 cm, and a standard deviation (SD) of 6 cm.

In Figure 5, a clear observation is that the range error highly depends on the position where the wearable sensor is placed on the body. In Figure 5a, we observe that the range error is very stable for the forehead position. Additionally, mean range errors of less than 20 cm are observed across all anchors. A possible reason for such a good performance lies in the fact that diffraction, and not direct transmission or even surface waves, is the dominant propagation mechanism on the human head [46]. Thus, in NLOS, the UWB waves are able to move into the shadow zone, with an increased path length of about 20 cm corresponding to the distance between the backhead and forehead.

In Figure 5b–g, we observe that the range error is highly unstable. The peaks observed correspond to large range errors obtained when the wearable sensor is lying in NLOS conditions with respect to the anchor. Figure 5 shows that, except for the forehead, the hand provides a better performance than the rest of the wearable sensor positions because, in NLOS, UWB wave propagates to the wearable sensor by creeping wave propagation [47], which is possibly enabled by the space between the chest and the hand (see Figure 3g).

In contrast to the forehead, Figure 5c shows that the chest position provides the worst ranging performance as errors of up to 4.5 m can be observed. The reason is that under NLOS the chest when interposed between anchor and wearable sensor generates a large area of shadow over the wearable sensor. This produces a challenging NLOS situation that does not allow the signal to arrive directly or by creeping waves around the body, but by reflections on surrounding objects.

In Figure 5d–g, we observe the range errors obtained when the wearable sensor is mounted on the limbs of the subject. The range errors are quite similar, with some differences arising from variations in the thickness of the limb where the sensor has been mounted.

6. Analyzing of the Positioning Performance

Because the main application of ranging is positioning, we compared the positioning performance of different body wearable positions. As explained above, the infrastructure of the experiments consisted of a wearable sensor mounted on seven body locations and four UWB anchors in fixed positions. To achieve the positioning performance, a localization algorithm based on the EKF was implemented. Note that we used range measurements from the continuous scenario.

Similar to Diez et al. [48] and Ridolfi et al. [49], for the implementation of the EKF, a white noise acceleration driven model was used as the dynamic model. This model was chosen because the pedestrian walked and stopped at different points for a few seconds, thus assuming a constant velocity model would not be appropriate.

Therefore, the state vector ${\mathit{x}}_k$ is given by the 3-D position ($\mathit{p}$) estimates as indicated in Equation (5) as:

$${\mathit{x}}_{k|k}={\mathit{x}}_k={\left({\mathit{p}}_k\right)}^T$$

(5)

${\mathit{x}}_k$ is defined as:

$${\mathit{x}}_{k|k-1}={\mathit{F}}_k{\mathit{x}}_{k-1|k-1}+{\mathit{w}}_k$$

(6)

where ${\mathit{F}}_k$ is the state transition matrix given as:

$${\mathit{F}}_k=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$$

(7)

${\mathit{w}}_k$ is the process noise, which we model as a white noise acceleration with covariance matrix ${\mathit{Q}}_k$:

$${\mathit{Q}}_k=\left(\begin{array}{ccc}{\sigma }_{ax}^2{\Delta T}^2/2& 0& 0\\ 0& {\sigma }_{ay}^2{\Delta T}^2/2& 0\\ 0& 0& {\sigma }_{az}^2{\Delta T}^2/2\end{array}\right)$$

(8)

$\Delta T$ is the difference in time between timestamps of the samples $\mathit{k}$ and $\mathit{k}-1$, and ${\sigma }_{ax}=100$ cm, ${\sigma }_{ay}=100$ cm, and ${\sigma }_{az}=10$ cm are the uncertainties that model the acceleration driving noise of the dynamic model in the x, y, and z directions, respectively. These values were set empirically.

The coordinates of the first ground-truth points were the initial inputs into the state vector ${\mathit{x}}_k$. Their initial standard deviations were set to 20 cm for the x and y coordinates, and 0.5 cm for the z coordinate. Note that we used a lower uncertainty in the vertical axis than in the horizontal plane because the height at which the wearable sensor was located on the body was fixed.

The measurement model has the form:

$${\mathit{z}}_k=\mathit{h}\left({\mathit{x}}_{k|k}\right)+{\mathit{n}}_k$$

(9)

where ${\mathit{z}}_k$ is the current measurements vector, $\mathit{h}$ is the measurement non-linear function, and ${\mathit{n}}_k$ is the measurement noise with covariance matrix ${\mathit{R}}_k$. For each wearable position, the ranges with the anchors were considered as inputs into the vector of measurements. During the update of the EKF, differences of 2.5 m between predicted and measured ranges were rejected because, in a sample time, i.e., 0.25 s, the subject could not move such a distance.

The SD of the measurement model was set according to

Table 4. The uncertainty in centimeters of the measurement model for each wearable sensor position.

	Ankle	Thigh	Forehead	Hand	Arm	Chest	Wrist
SD	50	60	10	30	50	130	20

. The values were obtained from a set of range measurements that were used to characterize the UWB nodes for each wearable sensor position.

Using range measurements from the four anchors to update the state estimate ${\mathit{x}}_{k|k}$, the measurements take on the following form:

$$z_{n,k}=h_n\left({\mathit{x}}_{k|k}\right)=$$

$$=\sqrt{{(p_x-a_{x,n})}^2+{(p_y-a_{y,n})}^2+{(p_z-a_{z,n})}^2}$$

(10)

where $z_{n,k}$ is a vector which contains the measured range between the nth anchor at the position $a_{x,n},a_{y,n}$, $a_{z,n}$, and wearable sensor with current position estimates at $p_x,p_y$ and $p_z$. In the EKF algorithm, $z_{n,k}$ is updated every time a new range measurement is obtained from the anchors.

Because the output of the EKF filter generates a continuous estimation of the path (see Figure 6), it was necessary to detect the points when the subject stood still along the path. This was important for ground-truth coordinates to be estimated. Thus, we performed the following tasks:

• Smoothing: We applied a moving average filter to each position component. The length of the window was empirically set to 4 s.
• Filtering: A moving variance with window length of 4 s was set to minimize the number of outliers in the position estimation.
• A k-means clustering was applied to the filtered estimates to determine the ground-truth positions (extorted from the obtained centroids).

This procedure was repeated for each of the body wearable positions. Thus, the estimated ground-truth points are illustrated in Figure 7 for each body wearable sensor position.

7. Results and Discussion

Based on the absolute value of the real ground-truth positions minus values estimated by the EKF as the error metric, in this section, we compare the performance of the wearable body sensor positions with the performance of the wearable sensor when mounted on a tripod. To better see the performance results, we present the main statistics in

Table 5. Wearable positions with their localization error (in m). P90 is the 90th percentile.

Wearable Location	Mean	Median	P90	SD
Tripod	0.12	0.10	0.21	0.06
Forehead	0.20	0.21	0.35	0.11
Hand	0.35	0.26	0.62	0.33
Ankle	0.50	0.36	0.97	0.36
Wrist	0.62	0.52	1.14	0.48
Thigh	0.68	0.57	1.46	0.45
Arm	1.36	1.26	2.47	0.77
Chest	2.46	2.55	4.04	1.66

.

In Table 5, we observe a clear relationship between the localization performance and the body wearable sensor position. Most of the errors observed are caused by body shadowing of the wearable sensor by corresponding body position, i.e., limbs, thorax, and head. The errors likely to be caused by other obstacles such as furniture and chairs are smaller in proportion because: (i) obstacles are not so close to the path of the subject; (ii) except for the ankle, the rest of the body wearable positions are located at a height above these obstacles. Even for the ankle, the furniture has enough leg room below the table (height from floor to bottom of table rail) to create either LOS or body shadowed NLOS possibilities with the anchors (see Figure 1).

Overall, it can be observed that the forehead and the chest position give the best (see Figure 7a) and worst (see Figure 7c) possible localization performance, respectively. In fact, in comparison with other the body wearable sensors, the errors obtained by the forehead are closer to the error obtained when the wearable sensor is mounted on a tripod (see tripod in Table 5). In addition, 90% of the estimates were below the errors of 0.35 m and 4.04 m for the forehead and chest, respectively. Similar to the ranging error, the reason for such relatively good performance lies in the fact that the circular shape of the head allows the blocked signal to be diffracted to the wearable sensor in NLOS.

The performance of the chest is heavily influenced by NLOS conditions due to human body shadowing. In fact according to Bharadwaj et al. [50], the chest generates the highest multipath in comparison with other body wearable positions. Thus, it is highly likely that errors as high as 4.04 m can be attributed to the reflections from nearby objects in the surroundings. In tracking a pedestrian, the chest position can be recommended only if it is possible to install enough anchors to reduce the risk of NLOS.

After the forehead, the hand position obtains the second lowest errors as 90% of the estimates were below the error of 0.62 m. The hand performs better than the chest, although in both cases the wearable sensor is at the center of the torso.

Similar to the work in [37], we observed quite similar positioning results for the wearable sensors mounted on the limb of the user except for the arm. The small inconsistency, especially with the arm, can be attributed to the EKF, which adds dynamic information such that there is no direct translation between ranging and positioning results. However, among these positions, the ankle gives the best performance, as 90% of the estimates were below the error of 0.97 m. Following the performance of the ankle position are the wrist, thigh, and arm locations with 90th percentiles of 1.14 m, 1.46 m, and 2.47 m, respectively.

8. Conclusions

We present a study of the effects of the body wearable sensor positions on UWB localization accuracy. The experiments were performed with several LOS and NLOS conditions. While the positioning performance of forehead is superior, the performance for the chest position is the worst. Most of the errors were caused by the presence of human body between the wearable sensor and the anchors.

Therefore, future research will consider utilizing appropriate body shadowing mitigation techniques, i.e., ranging models that take into account the body shadowing effect to minimize the errors created by the body.