Weak Signal Extraction from Lunar Penetrating Radar Channel 1 Data Based on Local Correlation

Abstract

Knowledge of the subsurface structure not only provides useful information on lunar geology, but it also can quantify the potential lunar resources for human beings. The dual-frequency lunar penetrating radar (LPR) aboard the Yutu rover offers a Special opportunity to understand the subsurface structure to a depth of several hundreds of meters using a low-frequency channel (channel 1), as well as layer near-surface stratigraphic structure of the regolith using high-frequency observations (channel 2). The channel 1 data of the LPR has a very low signal-to-noise ratio. However, the extraction of weak signals from the data represents a problem worth exploring. In this article, we propose a weak signal extraction method in view of local correlation to analyze the LPR CH-1 data, to facilitate a study of the lunar regolith structure. First, we build a pre-processing workflow to increase the signal-to-noise ratio (SNR). Second, we apply the K-L transform to separate the horizontal signal and then use the seislet transform (ST) to reserve the continuous signal. Then, the local correlation map is calculated using the two denoising results and a time–space dependent weighting operator is constructed to suppress the noise residuals. The weak signal after noise suppression may provide a new reference for subsequent data interpretation. Finally, in combination with the regional geology and previous research, we provide some speculative interpretations of the LPR CH-1 data.

1. Introduction

Chang’E-3 (CE-3) landed at 340.4875 °E, 44.1189 °N on the Moon on 14 December 2013, in a new region in the largest basin that had not been explored before, that is, the Mare Imbrium [1]. The dual-frequency lunar penetrating radar (LPR) aboard the Yutu Rover provides a special opportunity to understand the subsurface structure to a depth of several hundreds of meters from the low-frequency channel (CH-1, 60 MHz). This also includes mapping the layer near-surface stratigraphic structure of the regolith from the high-frequency channel (CH-2A and CH-2B, 500 MHz) [2].

The LPR data processing process and its preliminary results were first proposed by the National Astronomical Observatories (NAOC) [3]. Preliminary analysis of the LPR observations, especially observations from CH-1, showed more than nine subsurface layers from the surface to a depth of ~360 m [1]. The 114-m-long profile measurement of the onboard lunar penetrating radar measured the thickness of the lunar weathering layer at approximately 5 m and detected three basement basalt units with depths of 195, 215, and 345 m. The radar measurements show that other methods underestimate the thickness of the global lunar regolith layer, and it shows the large volume after the last volcanic eruption [4]. Fa et al., Lai et al., and Zhang et al. speculated on the near surface structure by processing the raw CH-2B data [5,6,7]. Meanwhile, Dong et al. and Zhang et al. calculated the parameters of the regolith [8,9].

Owing to the complex environment of moon acquisition, the LPR data, especially the CH-1 data, contains various types of noise. Useful weak signals that are distorted by this noise are difficult to identify, thereby limiting the subsequent data interpretation [10,11]. Moreover, the observable signals (3700 and 5800 ns) were proven to be false signals caused by the instrumentation [11]. To take full advantage of the CH-1 data, we focused on highlighting the weak signals to study the lunar structure. Previous researches indicate that the terrain of the LPR coverage is relatively flat [1], so the target signal is a horizontal signal with a certain continuity.

Regarding the LPR CH-1 data, there are still a lot of noise residuals in the denoised section owing to the high noise level. Liu et al. proposed a stacking method using local correlation to solve the problem of noise residuals in the seismic stack profile. The basic principle of the local correlation denoising method is to preprocess the common-midpoint (CMP) gathers by the conventional denoising method, and calculate the local correlation coefficients of the CMP gathers before and after denoising. They assume that the local correlation coefficient of the effective signal is much larger than the noise, and based on this difference, construct a time-space variable weight operator to suppress the noise represented by the small coefficient before stack. Local correlation [12] is a typical local attribute used to measure the local similarity of two signals. It has been utilized in several seismic signal processing fields, such as image contrast [13,14], time-frequency analysis [15], and random noise attenuation [16,17].

In this paper, we proposed a weak signal extraction method based on local correlation to deal with the LPR CH-1 data, and then we studied the structure of the lunar regolith. To extract these weak signals, we chose the K-L transform and seislet transform (ST) to process the LPR data. The K-L transform [18] can decompose 2D signals into sub-signals corresponding to a series of eigenvalues, which represent the strength of the horizontal coherence. It is often used to extract coherent signals or to eliminate random noise from the 2D seismic data [19]. The ST [20] is a sparse transform, which can utilize the local dip information to map signals into subsets with different frequencies and dips. After the transformation process, the continuous signal can be highlighted based on this property. Therefore, it is applicable to random noise suppression [21], deblending [22], and data reconstruction [23,24]. First, we built a pre-processing workflow to improve the signal-to-noise ratio (SNR). Second, we applied the K-L transform to reserve the horizontal signal, and the ST to reserve continuous signal, respectively. Then, the local correlation map was calculated using the two denoising results and a time–space dependent weighting operator was constructed to suppress the noise residuals. The weak signal after noise suppression can provide a new reference for subsequent data interpretation. Finally, combining with the regional geology and previous research, particularly on LPR data, we provide some speculative interpretations of the LPR CH-1 data.

2. Methods

2.1. Data Preprocessing

The lunar penetrating radar (LPR) track extends 114.8 m (Figure 1) near to Sinus Iridum. Two bottom sides of the top board of the moon rover mount two CH1 antennas respectively. The bottom board of the lunar rover mount the CH2 antenna. Each of the CH-1 antennas is mounted in a tubular radome. The monopole antenna has a radome for support and protection. The radome has a length of 1150 mm and a diameter of 12 mm. The spacing between the transmitting antenna and the receiving antenna is about 800 mm. In order to generate pulse waves to propagate along with the antenna without reflection, the Wu-King impedance loading method is used to load the antenna through a continuous resistance load from the feed point to the end of the antenna. In practice, it is usually difficult to generate a continuous distribution of resistance load. Therefore, a piecewise loading method which called concentrated resistive loading is usually used (Figure 2b).

The CH-2 transceiver antenna is mounted at the bottom of the lunar rover, which is approximately 30 cm from the ground. We can see the structure of the antenna from Figure 2c. The CH-2 antenna has three antenna elements. The antenna elements are arranged side by side in a metal back cavity which is divided into three separate cavities. One of the components is used to transmit EM waves, while the other two are used to receive EM waves [2].

In this section, the data preprocessing effects of the LPR CH-1 data are reported. As the focus is the subsurface structure, the CH-1 data was selected. Based on the acquisition parameters, the actual situation, and the data quality, an LPR data preprocessing flow was designed (Figure 3). The CH-1 image (an output of Figure 3) was accessible after data preprocessing.

Owing to various types of electromagnetic waves in lunar space, the complex terrain on the moon, and the harsh environment, LPR data has a low signal-to-noise ratio (SNR). In the shallow part (Figure 4, red box) of the pre-processed CH-1 data, there were several harsh horizontal noises. Irrespective of whether we used the averaging tracks or the sliding filter, etc., the noise could not be effectively eliminated and, therefore, it affected the extraction of useful information from the data. In the deep part, two obvious events were found at 3700 ns and 5800 ns (blue arrows). Regrettably, Li et al. proved that these were distortions from the instrumentation [11]. In summary, the CH-1 data of the LPR had a very low signal-to-noise ratio, raising the problem of how to extract the weak signals from the deep part.

2.2. Weak Signal Extraction Method Based on Local Correlation

The acquired field data could be considered as a collection of signals and noise. Noise attenuation involves suppressing the noise as much as possible while preserving the signal. However, the denoising effect is limited by the incompleteness of the denoising assumption and the close amplitude of the weak signal and noise. Therefore, for most denoising methods, the choice of denoising parameters is a trade-off between signal preservation and noise attenuation. To preserve the weak signal and simplify parameter selection, we introduced local correlation to the LPR data processing. First, we reviewed the definition of local correlation [12]. The global correlation coefficients $\gamma$ between two signals $a_i$ and $b_i$ can be defined as

$$\gamma =\frac{{\displaystyle \sum _{i=1}^N{a}_i{b}_i}}{\sqrt{{\displaystyle \sum _{i=1}^N{a}_i^2{b}_i^2}}},$$

(1)

where N is the number of signal elements. To measure the similarity between the two signals in a local way, the local correlation coefficients can be defined using a sliding window:

$${\gamma }_w(t)=\frac{{\displaystyle \sum _{i=t-w/2}^{t+w/2}{a}_i{b}_i}}{\sqrt{{\displaystyle \sum _{i=t-w/2}^{t+w/2}{a}_i^2{\displaystyle \sum _{i=t-w/2}^{t+w/2}{b}_i^2}}}},$$

(2)

where w is the size of the sliding window.

Fomel redefines the local correlation in a smoother way [12]. Based on linear algebra theory, Equation (1) can be rewritten as

$${\gamma }^2={\gamma }_1{\gamma }_2$$

(3)

where ${\gamma }_1$ and ${\gamma }_2$ are obtained by solving the optimization problem in the least squares sense:

$${\gamma }_1=\arg \underset{{\gamma }_1}{\min }{\Vert a-{\gamma }_{1}b\Vert }_2^2={(a^{T}a)}^{-1}(a^{T}b),$$

(4)

$${\gamma }_2=\arg \underset{{\gamma }_2}{\min }{\Vert a-{\gamma }_{2}b\Vert }_2^2={(b^{T}b)}^{-1}(b^{T}a),$$

(5)

where $a$,$b$ is the vector form of $a_i$,$b_i$. Meanwhile, $A$ and $B$ are written as two diagonal matrices where the main diagonal elements are $a$ and $b$, respectively. Then, this is followed by containing a shaping regularization [20]. The optimization problem in the least squares sense can then be modified as follows:

$$c_1={\left[{\lambda }_1^{2}I+S_m(A^{T}A-{\lambda }_1^{2}I)\right]}^{-1}{S}_m{A}^{T}b,$$

(6)

$$c_2={\left[{\lambda }_2^{2}I+S_m(B^{T}B-{\lambda }_2^{2}I)\right]}^{-1}{S}_m{B}^{T}a,$$

(7)

where $c_1$, $c_2$ are the vector form of ${\gamma }_1$ and ${\gamma }_2$ $S_m$ is a function for smoothness promotion; ${\lambda }_1$ and ${\lambda }_2$ are the two stable parameters used in the process of inversion to accelerate the convergence speed. We can select ${\lambda }_1$ and ${\lambda }_2$ as follows:

$${\lambda }_1={\Vert A^{T}A\Vert }_2,$$

(8)

$${\lambda }_2={\Vert B^{T}B\Vert }_2.$$

(9)

The basic idea of our methods is extracting the weak useful signals based on the local correlation difference between signal and noise. The local correlation is calculated by two different denoising results, therefore the selection of denoising methods is the key to our method. We select the denoising methods based on the LPR CH-1 data and previous researches [1]. From Figure 3, the observable useful signals indicate that the terrain of the LPR coverage is relatively flat, so the target signal is a horizontal signal with a certain continuity. To highlight the different characteristics of CH-1 data (horizontal and continuity), we chose the K-L transform (Appendix A) and ST (Appendix B) to process the LPR data. To preserve the deep weak signals, the ability to suppress noise was limited. Since the assumptions of different denoising methods are different, we considered that the noise residuals corresponding to the denoising results were different. Based on the similarity difference, a time–space dependent weighting operator [24] was proposed to extract weak signals and suppress noise residuals:

$$W(t,x)=\{\begin{array}{cc}1& c_{n,s}(t,x)>v_2\\ \frac{{\gamma }_{n,s}(t,x)-v_1}{v_2-v_1}& {\mathrm{v}}_1\le c_{n,s}(t,x)\le v_2 \\ 0& c_{n,s}(t,x)<v_1\end{array},$$

(10)

where $c_{n,s}(t,x)$ is the local correlation map, and $v_1$, $v_2$ are the thresholds that divide the local correlation map into three parts (Figure 5). $v_1$ defines the pure noise section, where the weighting operator $W$ will remove the entire section. $v_2$ defines the purely useful signal section, where the weighting operator $W$ will preserve the entire signal. When the local correlation coefficient is in the range of $v_1$ to $v_2$, the weak signal and noise are combined in that section, and the threshold function varies in a weighted length manner.

Note that $v_1$, $v_2$ controls the degree of signal extraction. To extract all the detectable useful events and attenuate some noise, we determine $v_1$, $v_2$ based on the average of similarity coefficients in pure noise section and purely signal section. The pure signal section covers the first few events, which have large and apparent similarity coefficients. And pure signal section covers the last few detectable events, which have small similarity coefficients.

We utilized the weighting operator on the two denoising results ($D_{\mathrm{KL}}$ and $D_{\mathrm{ST}}$), and then stacked the weighted outputs to obtain the extracted signal $D$:

$$D=\frac{W(D_{\mathrm{KL}})+W(D_{\mathrm{ST}})}{2}.$$

(11)

The specific workflow was as shown:

• Use the K-L transform to highlight horizontal signals,
• Use the ST to highlight continuous signals,
• Calculate the local correlation map based on the two pre-denoised results, and then construct the weighting operator,
• Utilize the operator to extract signals with high similarity,
• Stack the signal sections extracted from the denoising results.

The proposed method extracted weak signals using the similarity difference between signals and noise. Therefore, the choice of denoising parameters was more elegant, which avoided weak signal damage. Moreover, this method could take advantage of different denoising methods to improve the final weak signal extraction results.

3. Simulated Data Test

Figure 6 demonstrates the workflow of the proposed method. As mentioned above, the target weak signal is the horizontal signal with a certain continuity. Therefore, we present a noisy horizontal signal to test the effectiveness of the proposed method. The signal (Figure 6a) contains five events with different slowness, i.e., $(0,0,3,-4,-2)\cdot {10}^{-5}$ and we add Gaussian random noise to obtain s noisy signal (Figure 6b). Then we calculated the local correlation map (Figure 6e) between the two pre-denoised results (Figure 6c,d) and built the local correlation based weighting operator with $v_1=0.1,v_2=0.4$., and Figure 6f was the final result. The weak signal (60 ns) was distorted by noise. Both the K-L transform and ST suppressed some of the noise, but we still observed noise residuals in the denoised section. The local correlation map indicated the similarity difference between noise residuals and weak signals. Noise residuals were well attenuated by the weighting operator. To quantitatively compare the effects of weak signal extraction, we calculated the SNR of the denoising result:

$$\mathrm{SNR}=10{\log }_{10}\frac{{\Vert d_{\mathrm{signal}}\Vert }_2^2}{{\Vert d_{\mathrm{noisy}}-d_{\mathrm{denoise}}\Vert }_2^2},$$

(12)

where $d_{\mathrm{noisy}}$ is the noisy signal, and $d_{\mathrm{signal}}$, $d_{\mathrm{denoise}}$ are the signal section and denoised section, respectively.

Table 1. Comparison of the signal-to-noise ratio (SNR).

Data	Noisy Data	K-L	ST	Proposed Method
SNR	−9.02	8.42	6.32	15.13

shows the signal-to-noise ratio obtained by the four processing methods. As is well known, a larger SNR value indicates a stronger signal. Therefore, the local correlation algorithm used in this paper can obtain a better signal to noise ratio.

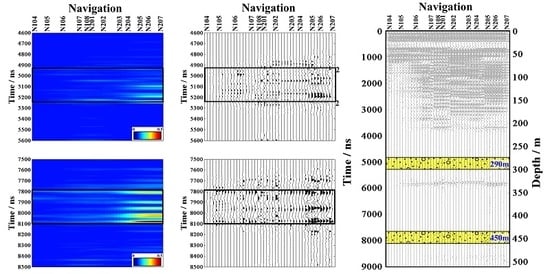
4. Results

In this section, we applied the K-L transform and ST to pre-denoise the LPR CH-1 data. Then we calculated the local correlation map between the two denoised results and built the weighting operator. After thresholding using the weighting operator, we stacked the two processed datasets to highlight the weak signal. Finally, we interpreted the processed LPR data. In the interpretation, we extracted two layers of the paleoregolith which separated the covered basalts in different periods.

Figure 7 shows the pre-denoised results using the K-L transform and ST. From Figure 7, we observe that the residuals in the denoised sections were quite different, which showed the different advantages of denoising methods.

Figure 8 shows the final extracted signal using our method. Besides the extracted weak signal, the false signals (3700 and 5800 ns) were also extracted. The reason was the large amplitude and high continuity in the noisy section, which showed the effectiveness of signal extraction using local correlation. Note that the selection of denoising methods varies with the target signal. For example, to extract signals from random noise, we can select the f-x deconvolution, median filter, bandpass filter, etc.

Furthermore, we also observed some suspected signals in Figure 8a,b, especially in the ranges 4950–5300 ns and 7750–8100 ns. Figure 9 shows the zoomed section of the two suspected signals. The two extracted signals denoted the large similarity in the local correlation map, which meant that the extracted signals had a certain continuity in the horizontal direction.

After the time–depth conversion, Figure 10 shows the result of the data. Except for the false signals (3700 and 5800 ns), we also extracted two layers of weak reflection at ~290 m and ~450 m. According to the formation mechanism of the mare [25,26], the Mare Imbrium is covered by basalts during different historical periods. After each basalt layer was covered, during that time interval, ancient regolith was formed, due to the impact of various meteorites. Based on the two weakly reflected events that we extracted from the CH-1 data, we explained these two layers (Figure 11). During the formation of Mare Imbrium, two layers of the paleoregolith at 290 m and 450 m were formed. The thickness of both is about 10 m.

5. Discussions

Xiao et al. show that at least nine underground horizons can be determined by LPR data and comprehensive geological interpretation, indicating that the area has undergone complex geological processes, since the Imbrian is compositionally distinct from the Apollo and Luna landing site [1]. Zhang et al. reveal the in situ spectral reflectance and elemental analysis of the lunar soil at the landing site. The young basalt can be from the mantle reservoir rich in ilmenite and then assimilated by 10-20% of the last residual melt in the lunar magma ocean [4]. Yuan et al. interpret as different period lava flow sequences deposited on the lunar surface. The most probable directions of these flows were inferred from layer depths, thicknesses, and other geological information. Moreover, the apparent Imbrian paleoregolith homogeneity in the profile supports the suggestion of a quiescent period of lunar surface evolution. Similar subsurface structures are found at the NASA Apollo landing sites, indicating that the cause and time of formation of the imaged phenomena may be similar between the two distant regions [27].

It should be noted that the above-mentioned layer judgment is performed under the condition that the CH-1 data is reliable and true. However, Li et al.’s paper tries to solve this controversy by carefully analyzing and comparing the data collected by the Yutu rover on the moon and the LPR prototype of the CE-3 lunar rover model installed on the ground. This analysis shows that deep radar features previously attributed to lunar shallow stratum are not true reflectors, but rather they may be signal artifacts produced by the system and their electromagnetic interaction with metal rover [11].

Based on the local correlation method, we extracted two layers of weak reflection at ~290 m and ~450 m. According to the formation mechanism of the mare, after each basalt layer was covered, during that time interval, ancient regolith was formed, due to the impact of various meteorites. During the formation of Mare Imbrium, two layers of the paleoregolith at 290 m and 450 m were formed. The thickness of both is about 10 m.

Our result avoids the extracted events mentioned by Li et al. And we propose two new weakly reflective layers after Xiao et al. These two new reflective layers enhance the deep utilization of CH-1 data to some extent.

The proposed method is based on the assumption that the noise residuals by different denoising methods are orthogonal which have a small value of local correlation coefficients, and useful signals are just the opposite. The local correlation-based methods not only can deal with random noise, but also coherent noise [28]. Due to the complex moon acquisition conditions, the LPR data contains various types of noise. Strong noise adaptability makes the proposed method more promising in LPR data processing.

Another advantage of the proposed method is balancing the advantages of different denoising methods, even the conventional methods. And the most important step of our method is the selection of denoising method. The choices of denoising method are determined by the target signal characteristics. For CH-1 data, the denoising method which highlights horizontal and continuous signal is selected. Furthermore, the useful signals in CH-2 data are interfered by rocks caused diffraction noise [7], the dip filtering methods are more applicable, such as a f-k filter.

6. Conclusions

In this paper, we proposed a weak signal extraction method based on local correlation to deal with LPR CH-1 data, and then we studied the structure of the lunar regolith. First, we built a pre-processing workflow to improve the signal-to-noise ratio (SNR). Second, we applied the K-L transform to reserve horizontal signals, and the ST to reserve continuous signals, respectively. Then, the local correlation map was calculated according to the two denoising results, and a time–space dependent weighting operator was constructed to suppress the noise residuals. The weak signal after noise suppression can provide a new reference for subsequent data interpretation. Finally, combining with previous research and the LPR data, we provided some speculative interpretations of the LPR CH-1 data.

Except for the false signals, we extracted two layers of weak reflection at ~290 m and ~450 m. According to the formation mechanism of the mare, the two layers are explained from the two weakly reflected events. During the formation of Mare Imbrium, two layers of paleoregolith at 290 m and 450 m were formed. The thickness both was about 10 m.

These results provide valuable information to understand the reflections of LPR data, and they offer a reference for future lunar missions.