Perspective on Commercial Li-ion Battery Testing, Best Practices for Simple and Effective Protocols
Abstract
:1. Introduction
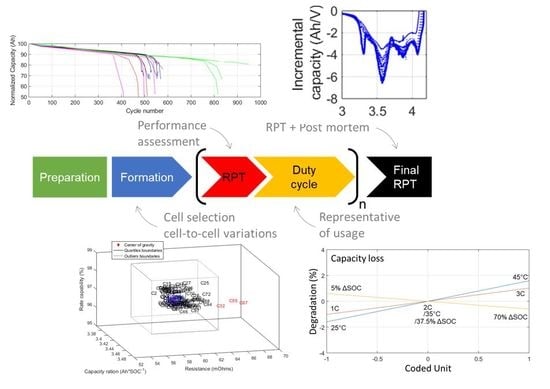
2. Methods and Discussion
2.1. Test Preparation
2.2. Formation
2.3. Reference Performance Test
2.4. Duty Cycle
2.5. Post-Mortem
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, T.; Glick, M.B.; Lee, J.-H. Island energy transition: Assessing Hawaii’s multi-level, policy-driven approach. Renew. Sustain. Energy Rev. 2020, 118. [Google Scholar] [CrossRef]
- Zhao, W.; Yi, J.; He, P.; Zhou, H. Solid-state electrolytes for lithium-ion batteries: Fundamentals, challenges and perspectives. Electrochem. Energy Rev. 2019, 2, 574–605. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wu, Z.; Zou, J.; Gao, P.; Niu, X.; Li, H.; Chen, L. Li-free cathode materials for high energy density lithium batteries. Joule 2019, 3, 2086–2102. [Google Scholar] [CrossRef]
- Shen, M.; Gao, Q. A review on battery management system from the modeling efforts to its multiapplication and integration. Int. J. Energy Res. 2019. [Google Scholar] [CrossRef]
- Plett, G.L. Review and some perspectives on different methods to estimate state of charge of lithium-Ion batteries. J. Automot. Saf. Energy 2019, 10, 249–272. [Google Scholar] [CrossRef]
- Meng, H.; Li, Y.-F. A review on prognostics and health management (PHM) methods of lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 116. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, J.; Xiong, R.; Shen, W.; He, H. Towards a smarter battery management system: A critical review on optimal charging methods of lithium ion batteries. Energy 2019. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Dubarry, M.; Somerville, L.; McGordon, A.; Jennings, P.; Bloom, I. A comparison of methodologies for the non-invasive characterisation of commercial Li-ion cells. Progr. Energy Combust. Sci. 2019, 72, 1–31. [Google Scholar] [CrossRef]
- Dubarry, M.; Baure, G.; Anseán, D. Perspective on state of health determination in lithium ion batteries. J. Electrochem. Energy Convers. Storage 2020, 1–25, in press. [Google Scholar] [CrossRef]
- Waldmann, T.; Iturrondobeitia, A.; Kasper, M.; Ghanbari, N.; Aguesse, F.; Bekaert, E.; Daniel, L.; Genies, S.; Jimenez Gordon, I.; Loble, M.; et al. Review—Post-mortem analysis of aged lithium-ion batteries: Disassembly methodology and physico-chemical analysis techniques. J. Electrochem. Soc. 2016, 163, A2149–A2164. [Google Scholar] [CrossRef]
- Lu, J.; Wu, T.; Amine, K. State-of-the-art characterization techniques for advanced lithium-ion batteries. Nat. Energy 2017, 2, 17011. [Google Scholar] [CrossRef]
- Taylor, J.; Barai, A.; Ashwin, T.R.; Guo, Y.; Amor-Segan, M.; Marco, J. An insight into the errors and uncertainty of the lithium-ion battery characterisation experiments. J. Energy Storage 2019, 24. [Google Scholar] [CrossRef]
- De-Leon, S. Battery safety training for portable & stationary applications. In Proceedings of the Next Generation Energy Storage, San Diego, CA, USA, 18–20 April 2016. [Google Scholar]
- Dubarry, M.; Qin, N.; Brooker, P. Calendar aging of commercial Li-ion cells of different chemistries—A review. Curr. Opin. Electrochem. 2018, 9, 106–113. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2017. [Google Scholar] [CrossRef]
- Börger, A.; Mertens, J.; Wenzl, H. Thermal runaway and thermal runaway propagation in batteries: What do we talk about? J. Energy Storage 2019, 24. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A review of lithium ion battery failure mechanisms and fire prevention strategies. Progr. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar] [CrossRef]
- Wu, X.; Song, K.; Zhang, X.; Hu, N.; Li, L.; Li, W.; Zhang, L.; Zhang, H. Safety issues in lithium Ion batteries: Materials and cell design. Front. Energy Res. 2019, 7. [Google Scholar] [CrossRef] [Green Version]
- Cripps, E.; Pecht, M. A bayesian nonlinear random effects model for identification of defective batteries from lot samples. J. Power Sources 2017, 342, 342–350. [Google Scholar] [CrossRef]
- An, F.; Chen, L.; Huang, J.; Zhang, J.; Li, P. Rate dependence of cell-to-cell variations of lithium-ion cells. Sci. Rep. 2016, 6, 35051. [Google Scholar] [CrossRef]
- Schuster, S.F.; Brand, M.J.; Berg, P.; Gleissenberger, M.; Jossen, A. Lithium-ion cell-to-cell variation during battery electric vehicle operation. J. Power Sources 2015, 297, 242–251. [Google Scholar] [CrossRef]
- Baumhöfer, T.; Brühl, M.; Rothgang, S.; Sauer, D.U. Production caused variation in capacity aging trend and correlation to initial cell performance. J. Power Sources 2014, 247, 332–338. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. Quantifying cell-to-cell variations in lithium Ion batteries. Int. J. Electrochem. 2012, 2012, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Shin, J. Screening process of Li-ion series battery pack for improved voltage soc balancing. In Proceedings of the International Power Electronics Conference, Sapporo, Japan, 21–24 June 2010. [Google Scholar]
- Rumpf, K.; Naumann, M.; Jossen, A. Experimental investigation of parametric cell-to-cell variation and correlation based on 1100 commercial lithium-ion cells. J. Energy Storage 2017, 14, 224–243. [Google Scholar] [CrossRef]
- Robertson, D.C.; Christophersen, J.P.; Bennett, T.; Walker, L.K.; Wang, F.; Liu, S.; Fan, B.; Bloom, I. A comparison of battery testing protocols: Those used by the U.S. advanced battery consortium and those used in China. J. Power Sources 2016, 306, 268–273. [Google Scholar] [CrossRef] [Green Version]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. Origins and accommodation of cell variations in Li-ion battery pack modeling. Int. J. Energy Res. 2010, 34, 216–231. [Google Scholar] [CrossRef]
- Devie, A.; Dubarry, M. Durability and reliability of electric vehicle batteries under electric utility grid operations. Part 1: Cell-to-cell variations and preliminary testing. Batteries 2016, 2, 28. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A. Battery durability and reliability under electric utility grid operations: Representative usage aging and calendar aging. J. Energy Storage 2018, 18, 185–195. [Google Scholar] [CrossRef]
- Devie, A.; Baure, G.; Dubarry, M. Intrinsic variability in the degradation of a batch of commercial 18650 Lithium-Ion cells. Energies 2018, 11, 1031. [Google Scholar] [CrossRef] [Green Version]
- Wood, D.L.; Li, J.; An, S.J. Formation challenges of lithium-ion battery manufacturing. Joule 2019, 3, 2884–2888. [Google Scholar] [CrossRef]
- Heubner, C.; Schneider, M.; Michaelis, A. Diffusion-limited c-rate: A fundamental principle quantifying the intrinsic limits of Li-Ion batteries. Adv. Energy Mater. 2019. [Google Scholar] [CrossRef] [Green Version]
- Peukert, W. An equation forrelating capacity to discharge rate. Electrotech. Z. 1897, 1, 287–288. [Google Scholar]
- Bard, A.; Faulkner, L. Electrochemical Methods—Fundamentals and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Liaw, B.Y.; Dubarry, M. A roadmap to understand battery performance in electric and hybrid vehicle operation. In Electric and Hybrid Vehicles; Pistoia, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 375–403. [Google Scholar] [CrossRef]
- Christophersen, J.P.; Ho, C.D.; Motloch, C.G.; Howell, D.; Hess, H.L. Effects of reference performance testing during aging using commercial Lithium-Ion cells. J. Electrochem. Soc. 2006, 153, A1406. [Google Scholar] [CrossRef]
- INL. Battery Test Manual For Electric Vehicles; INL: Idaho Falls, ID, USA, 2015. [Google Scholar]
- Soto, A.; Berrueta, A.; Sanchis, P.; Ursúa, A. Analysis of the main battery characterization techniques and experimental comparison of commercial 18650 Li-ion cells. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genova, Italy, 11–14 June 2019. [Google Scholar]
- Liu, C.; Neale, Z.G.; Cao, G. Understanding electrochemical potentials of cathode materials in rechargeable batteries. Mater. Today 2016, 19, 109–123. [Google Scholar] [CrossRef]
- Truchot, C.; Dubarry, M.; Liaw, B.Y. State-of-charge estimation and uncertainty for lithium-ion battery strings. Appl. Energy 2014, 119, 218–227. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Cugnet, M.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle applications. Part I: Initial characterizations. J. Power Sources 2011, 196, 10328–10335. [Google Scholar] [CrossRef]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Capacity loss in rechargeable lithium cells during cycle life testing: The importance of determining state-of-charge. J. Power Sources 2007, 174, 1121–1125. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Cell degradation in commercial LiFePO4 cells with high-power and high-energy designs. J. Power Sources 2014, 258, 408–419. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle applications. Part II. Degradation mechanism under 2C cycle aging. J. Power Sources 2011, 196, 10336–10343. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle applications: III. Effect of thermal excursions without prolonged thermal aging. J. Electrochem. Soc. 2013, 160, A191–A199. [Google Scholar] [CrossRef]
- Balewski, L.; Brenet, J.P. A new method for the study of the electrochemical reactivity of manganese dioxide. Electrochem. Technol. 1967, 5, 527–531. [Google Scholar]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Incremental capacity analysis and close-to-equilibrium OCV measurements to quantify capacity fade in commercial rechargeable lithium batteries. Electrochem. Solid State Lett. 2006, 9, A454–A457. [Google Scholar] [CrossRef]
- Dubarry, M.; Liaw, B.Y. Identify capacity fading mechanism in a commercial LiFePO4 cell. J. Power Sources 2009, 194, 541–549. [Google Scholar] [CrossRef]
- Bloom, I.; Christophersen, J.; Gering, K. Differential voltage analyses of high-power, lithium-ion cells. 2. Applications. J. Power Sources 2005, 139, 304–313. [Google Scholar] [CrossRef]
- Bloom, I.; Jansen, A.N.; Abraham, D.P.; Knuth, J.; Jones, S.A.; Battaglia, V.S.; Henriksen, G.L. Differential voltage analyses of high-power, lithium-ion cells. 1. Technique and applications. J. Power Sources 2005, 139, 295–303. [Google Scholar] [CrossRef]
- Bloom, I.; Christophersen, J.P.; Abraham, D.P.; Gering, K.L. Differential voltage analyses of high-power, lithium-ion cells. 3. Another anode phenomenon. J. Power Sources 2006, 157, 537–542. [Google Scholar] [CrossRef]
- Dubarry, M.; Berecibar, M.; Devie, A.; Anseán, D.; Omar, N.; Villarreal, I. State of health battery estimator enabling degradation diagnosis: Model and algorithm description. J. Power Sources 2017, 360, 59–69. [Google Scholar] [CrossRef]
- Dubarry, M.; Gaubicher, J.; Guyomard, D.; Wallez, G.; Quarton, M.; Baehtz, C. Uncommon potential hysteresis in the Li/Li2xVO(H2−xPO4)2 (0 ≤ x ≤ 2) system. Electrochim. Acta 2008, 53, 4564–4572. [Google Scholar] [CrossRef]
- Schindler, S.; Baure, G.; Danzer, M.A.; Dubarry, M. Kinetics accommodation in Li-ion mechanistic modeling. J. Power Sources 2019, 440, 227117. [Google Scholar] [CrossRef]
- Schindler, S.; Bauer, M.; Petzl, M.; Danzer, M.A. Voltage relaxation and impedance spectroscopy as in-operando methods for the detection of lithium plating on graphitic anodes in commercial lithium-ion cells. J. Power Sources 2016, 304, 170–180. [Google Scholar] [CrossRef]
- Wu, B.; Yufit, V.; Merla, Y.; Martinez-Botas, R.F.; Brandon, N.P.; Offer, G.J. Differential thermal voltammetry for tracking of degradation in lithium-ion batteries. J. Power Sources 2015, 273, 495–501. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; Liaw, B.Y. The value of battery diagnostics and prognostics. J. Energy Power Sources 2014, 1, 242–249. [Google Scholar]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Dahn, H.M.; Smith, A.J.; Burns, J.C.; Stevens, D.A.; Dahn, J.R. User-friendly differential voltage analysis freeware for the analysis of degradation mechanisms in Li-Ion batteries. J. Electrochem. Soc. 2012, 159, A1405–A1409. [Google Scholar] [CrossRef]
- HNEI. Alawa Central. Available online: https://www.soest.hawaii.edu/HNEI/alawa/ (accessed on 9 January 2020).
- Berecibar, M.; Devriendt, F.; Dubarry, M.; Villarreal, I.; Omar, N.; Verbeke, W.; Van Mierlo, J. Online state of health estimation on NMC cells based on predictive analytics. J. Power Sources 2016, 320, 239–250. [Google Scholar] [CrossRef]
- Abraham, D.P.; Knuth, J.L.; Dees, D.W.; Bloom, I.; Christophersen, J.P. Performance degradation of high-power lithium-ion cells—Electrochemistry of harvested electrodes. J. Power Sources 2007, 170, 465–475. [Google Scholar] [CrossRef]
- Kassem, M.; Delacourt, C. Postmortem analysis of calendar-aged graphite/LiFePO4 cells. J. Power Sources 2013, 235, 159–171. [Google Scholar] [CrossRef]
- Anseán, D.; Dubarry, M.; Devie, A.; Liaw, B.Y.; García, V.M.; Viera, J.C.; González, M. Fast charging technique for high power LiFePO4 batteries: A mechanistic analysis of aging. J. Power Sources 2016, 321, 201–209. [Google Scholar] [CrossRef]
- Schmid, A.U.; Kurka, M.; Birke, K.P. Reproducibility of Li-ion cell reassembling processes and their influence on coin cell aging. J. Energy Storage 2019, 24. [Google Scholar] [CrossRef]
- Murray, V.; Hall, D.S.; Dahn, J.R. A guide to full coin cell making for academic researchers. J. Electrochem. Soc. 2019, 166, A329–A333. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, Q.; Wang, S.; Ling, S.; Zheng, J.; Yu, X.; Li, H. A facile electrode preparation method for accurate electrochemical measurements of double-side-coated electrode from commercial Li-ion batteries. J. Power Sources 2018, 384, 172–177. [Google Scholar] [CrossRef]
- Wu, B.; Yang, Y.; Liu, D.; Niu, C.; Gross, M.; Seymour, L.; Lee, H.; Le, P.M.L.; Vo, T.D.; Deng, Z.D.; et al. Good practices for rechargeable lithium metal batteries. J. Electrochem. Soc. 2019, 166, A4141–A4149. [Google Scholar] [CrossRef]
- Baure, G.; Devie, A.; Dubarry, M. Battery durability and reliability under electric utility grid operations: Path dependence of battery degradation. J. Electrochem. Soc. 2019, 166, A1991–A2001. [Google Scholar] [CrossRef]
- Dubarry, M.; Baure, G.; Devie, A. Durability and reliability of EV batteries under electric utility grid operations: Path dependence of battery degradation. J. Electrochem. Soc. 2018, 165, A773–A783. [Google Scholar] [CrossRef]
- Devie, A.; Dubarry, M.; Liaw, B.Y. Overcharge study in Li4Ti5O12 based Lithium-Ion pouch cell: I. Quantitative diagnosis of degradation modes. J. Electrochem. Soc. 2015, 162, A1033–A1040. [Google Scholar] [CrossRef]
- Anseán, D.; Baure, G.; González, M.; Cameán, I.; García, A.B.; Dubarry, M. Mechanistic investigation of Silicon–Graphite//LiNi0.8Mn0.1Co0.1O2 commercial cells for non-intrusive diagnosis and prognosis. J. Power Sources 2020. submitted. [Google Scholar]
- Baure, G.; Dubarry, M. Synthetic vs. real driving cycles: A comparison of electric vehicle battery degradation. Batteries 2019, 5, 42. [Google Scholar] [CrossRef] [Green Version]
- Anseán, D.; Dubarry, M.; Devie, A.; Liaw, B.Y.; García, V.M.; Viera, J.C.; González, M. Operando lithium plating quantification and early detection of a commercial LiFePO 4 cell cycled under dynamic driving schedule. J. Power Sources 2017, 356, 36–46. [Google Scholar] [CrossRef] [Green Version]
- Gering, K.L.; Sazhin, S.V.; Jamison, D.K.; Michelbacher, C.J.; Liaw, B.Y.; Dubarry, M.; Cugnet, M. Investigation of path dependence in commercial lithium-ion cells chosen for plug-in hybrid vehicle duty cycle protocols. J. Power Sources 2011, 196, 3395–3403. [Google Scholar] [CrossRef]
- Wu, W.; Wu, W.; Qiu, X.; Wang, S. Low-temperature reversible capacity loss and aging mechanism in lithium-ion batteries for different discharge profiles. Int. J. Energy Res. 2018, 43, 243–253. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishnan, K.N.; Coupar, T.; Nelson, D.J.; Ellis, M.W. Experimental evaluation of the effect of cycle profile on the durability of commercial Lithium Ion power cells. J. Electrochem. Energy Convers. Storage 2019, 16. [Google Scholar] [CrossRef]
- Klett, M.; Eriksson, R.; Groot, J.; Svens, P.; Ciosek Högström, K.; Lindström, R.W.; Berg, H.; Gustafson, T.; Lindbergh, G.; Edström, K. Non-uniform aging of cycled commercial LiFePO4//graphite cylindrical cells revealed by post-mortem analysis. J. Power Sources 2014, 257, 126–137. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Charging protocols for lithium-ion batteries and their impact on cycle life—An experimental study with different 18650 high-power cells. J. Energy Storage 2016, 6, 125–141. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Dubarry, M. From driving cycle analysis to understanding battery performance in real-life electric hybrid vehicle operation. J. Power Sources 2007, 174, 76–88. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; Stein, K.; Tun, M.; Matsuura, M.; Rocheleau, R. Battery energy storage system battery durability and reliability under electric utility grid operations: Analysis of 3 years of real usage. J. Power Sources 2017, 338, 65–73. [Google Scholar] [CrossRef]
- Montgomery, D. Design and Analysis of Experiments, 8th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Antony, J. Design of Experiments for Engineers and Scientists; Elsevier Science & Technology Books: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Rynne, O.; Dubarry, M.; Molson, C.; Nicolas, E.; Lepage, D.; Prébé, A.; Aymé-Perrot, D.; Rochefort, D.; Dollé, M. Designs of experiments to optimize Li-ion battery electrodes’ formulation. J. Electrochem. Soc. 2020, submitted. [Google Scholar]
- Rynne, O.; Dubarry, M.; Molson, C.; Lepage, D.; Prébé, A.; Aymé-Perrot, D.; Rochefort, D.; Dollé, M. Designs of experiments for beginners—A quick start guide for application to electrode formulation. Batteries 2019, 5, 72. [Google Scholar] [CrossRef] [Green Version]
- Su, L.; Zhang, J.; Wang, C.; Zhang, Y.; Li, Z.; Song, Y.; Jin, T.; Ma, Z. Identifying main factors of capacity fading in lithium ion cells using orthogonal design of experiments. Appl. Energy 2016, 163, 201–210. [Google Scholar] [CrossRef]
- Cui, Y.; Du, C.; Yin, G.; Gao, Y.; Zhang, L.; Guan, T.; Yang, L.; Wang, F. Multi-stress factor model for cycle lifetime prediction of lithium ion batteries with shallow-depth discharge. J. Power Sources 2015, 279, 123–132. [Google Scholar] [CrossRef]
- Prochazka, W.; Pregartner, G.; Cifrain, M. Design-of-experiment and statistical modeling of a large scale aging experiment for two popular Lithium Ion cell chemistries. J. Electrochem. Soc. 2013, 160, A1039–A1051. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; McKenzie, K. Durability and reliability of electric vehicle batteries under electric utility grid operations: Bidirectional charging impact analysis. J. Power Sources 2017, 358, 39–49. [Google Scholar] [CrossRef]
- Mathieu, R.; Baghdadi, I.; Briat, O.; Gyan, P.; Vinassa, J.-M. D-optimal design of experiments applied to lithium battery for ageing model calibration. Energy 2017, 141, 2108. [Google Scholar] [CrossRef]
- Baghdadi, I.; Mathieu, R.; Briat, O.; Gyan, P.; Vinassa, J.-M. Lithium-ion battery ageing assessment based on a reduced design of experiments. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017. [Google Scholar]
- Rohr, S.; Müller, S.; Baumann, M.; Kerler, M.; Ebert, F.; Kaden, D.; Lienkamp, M. Quantifying uncertainties in reusing Lithium-Ion batteries from electric vehicles. Procedia Manuf. 2017, 8, 603–610. [Google Scholar] [CrossRef]
- Harris, S.J.; Harris, D.J.; Li, C. Failure statistics for commercial lithium ion batteries: A study of 24 pouch cells. J. Power Sources 2017, 342, 589–597. [Google Scholar] [CrossRef] [Green Version]
- Dubarry, M.; Pastor-Fernández, C.; Baure, G.; Yu, T.F.; Widanage, W.D.; Marco, J. Battery energy storage system modeling: Investigation of intrinsic cell-to-cell variations. J. Energy Storage 2019, 23, 19–28. [Google Scholar] [CrossRef]
- Dubarry, M.; Baure, G.; Pastor-Fernández, C.; Yu, T.F.; Widanage, W.D.; Marco, J. Battery energy storage system modeling: A combined comprehensive approach. J. Energy Storage 2019, 21, 172–185. [Google Scholar] [CrossRef]
- Lewerenz, M.; Fuchs, G.; Becker, L.; Sauer, D.U. Irreversible calendar aging and quantification of the reversible capacity loss caused by anode overhang. J. Energy Storage 2018, 18, 149–159. [Google Scholar] [CrossRef]
- Lewerenz, M.; Warnecke, A.; Sauer, D.U. Introduction of capacity difference analysis (CDA) for analyzing lateral Lithium-Ion flow to determine the state of covering layer evolution. J. Power Sources 2017, 354, 157–166. [Google Scholar] [CrossRef]
- Kovachev, G.; Schröttner, H.; Gstrein, G.; Aiello, L.; Hanzu, I.; Wilkening, H.M.R.; Foitzik, A.; Wellm, M.; Sinz, W.; Ellersdorfer, C. Analytical dissection of an automotive Li-Ion pouch cell. Batteries 2019, 5, 67. [Google Scholar] [CrossRef] [Green Version]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubarry, M.; Baure, G. Perspective on Commercial Li-ion Battery Testing, Best Practices for Simple and Effective Protocols. Electronics 2020, 9, 152. https://doi.org/10.3390/electronics9010152
Dubarry M, Baure G. Perspective on Commercial Li-ion Battery Testing, Best Practices for Simple and Effective Protocols. Electronics. 2020; 9(1):152. https://doi.org/10.3390/electronics9010152
Chicago/Turabian StyleDubarry, Matthieu, and George Baure. 2020. "Perspective on Commercial Li-ion Battery Testing, Best Practices for Simple and Effective Protocols" Electronics 9, no. 1: 152. https://doi.org/10.3390/electronics9010152
APA StyleDubarry, M., & Baure, G. (2020). Perspective on Commercial Li-ion Battery Testing, Best Practices for Simple and Effective Protocols. Electronics, 9(1), 152. https://doi.org/10.3390/electronics9010152