Fast “Feast/Famine” Cycles for Studying Microbial Physiology Under Dynamic Conditions: A Case Study with Saccharomyces cerevisiae
Abstract
:1. Introduction
2. Results and Discussion
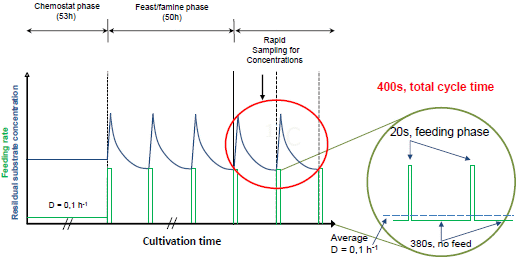
2.1. The Feast/Famine Setup is a Robust Dynamic System for Metabolic Studies
2.2. Reconstruction of Specific O2 and CO2 Rates during a Cycle

2.3. The Feast/Famine vs. the Reference Chemostat Cultivation
| Rate | Steady state a | Feast/famine b |
|---|---|---|
| Biomass concentration (gDW/L) | 3.64 ± 0.16 | 3.46 ± 0.17 |
| qS (mmol Cmol−1h−1) | 30.1 ± 0.9 | 30.7 ± 0.3 |
| Μ (mCmol Cmol−1h−1) | 100.9 ± 0.2 | 99.9 ± 0.6 |
| qCO2 (mmol Cmol−1h−1) | 74.6 ± 5.4 | 73.2 ± 1.4 |
| qO2 (mmol Cmol−1h−1) | 70.0 ± 5.4 | 70.4 ± 1.0 |
| qAcet (mmol Cmol−1h−1) | 2.7 ± 0.1 | 5.7 ± 0.6 |
| Residual glucose (mM) | 0.183 ± 0.002 | Max: 0.460 ± 0.01 Min: 0.094 ± 0.005 |
| RQ | 1.065 | 1.040 |
2.4. The Feast/Famine Platform Has Interesting Features for Studying In Vivo Kinetics under Dynamic Conditions
| Variable | Theobald et al., 1997 | Mashego et al., 2006 | Van Kleeff et al., 1996 | This study |
|---|---|---|---|---|
| Glucose perturbation | Pulse in STR | Pulse in STR/Bioscope | Block-wise feeding to STR | Block-wise feeding to STR |
| Strain | CBS7336 | CEN.PK113-7D | CBS8066 | CEN.PK113-7D |
| Dilution rate (h−1) | 0.1 (before pulse) | 0.05 (before pulse) | 0.05 (average) | 0.1 (average) |
| Min/Max. extracellular glucose concentration (mM) | 0.07/5.5 | 0.11/2.8 | ~0/0.15 | 0.094/0.46 |
| Observed by-products | Ethanol, Acetate, Glycerol | Ethanol, Acetate | None | Acetate |
| Min/Max qS (mmol/Cmol/h) | 33/190 | Not reported | Not reported | 5/90 |
2.5. Dynamic Metabolic Response of S. cerevisiae to Feast/Famine Perturbations
2.5.1. Extracellular Glucose Uptake Dynamics, the Entry Gate to Central Metabolism


2.5.2. The Energy and Redox Dynamics during the Cycle: With the Feast/Famine the Typical ATP Paradox Is not Observed

2.6. Possible Metabolic and Regulatory Mechanisms
2.6.1. The Dynamics of Metabolites of the Glycolysis and the Pentose Phosphate Pathway


2.6.2. Dynamics of the Storage Carbohydrate Intermediates

2.6.3. Dynamics of the TCA Cycle Intermediates

2.7. Thermodynamic Analysis of Different Biochemical Reactions


3. Experimental Section
3.1. Strain and Culture Conditions
3.2. Feast Famine Setup

3.3. Acquisition, Processing and Analysis of Samples
3.3.1. Extracellular Metabolites
3.3.2. Rate Reconciliation
3.3.3. Intracellular Metabolites
4. Conclusions
Abbreviations
Metabolites
| 2PG | 2-phosphoglycerate |
| 3PG | 3-phosphoglycerate |
| 6PG | 6-phospho gluconate |
| α-KG | oxoglutarate |
| ALA | alanine |
| ASP | aspartate |
| CoA | coenzyme-A |
| DHAP | dihydroxy acetone phosphate |
| E4P | erythrose-4-phosphate |
| F6P | fructose-6-phosphate |
| FBP | fructose-1,6-bis-phosphate |
| FUM | fumarate |
| G1P | glucose-1-phosphate |
| G6P | glucose-6-phosphate |
| GAP | glyceraldehyde-3-phosphate |
| GLN | glutamine |
| GLU | glutamate |
| GLY | glycine |
| Iso-Cit | isocitrate |
| LEU | leucine |
| LYS | lysine |
| MAL | malate |
| METH | methionine |
| OAA | oxaloacetate |
| PEP | phospho-enol-pyruvate |
| PRO | proline |
| PYR | pyruvate |
| R5P | ribose-5-phosphate |
| Ribu5P | ribulose-5-phosphate |
| SER | serine |
| S7P | sedoheptulose-7-phosphate |
| SUC | succinate |
| T6P | trehalose-6-phosphate |
| UDPG | UDP-glucose |
| UDP | uridine-5-diphosphate |
| UTP | uridine-5-triphosphate |
| X5P | xylulose-5-phosphate. |
Enzymes and/or the reactions they catalyze
| ACO | aconitate hydratase |
| AK | adenylate kinase |
| ENO | phosphopyruvate hydratase |
| FBA | fructose-bisphosphate aldolase |
| FMH | fumarate hydratase |
| G6PDH | glucose-6-phosphate dehydrogenase |
| GAPDH&PGK | glyceraldehyde-3-phosphate dehydrogenase + phosphoglycerate kinase |
| GPM | phosphoglycerate mutase |
| PFK | 6-phosphofructokinase |
| PGI | glucose-6-phosphate isomerase |
| PGM | phosphoglucomutase |
| PMI | mannose-6-phosphate isomerase |
| PYK | pyruvate kinase |
| RPE | ribulose-phosphate 3-epimerase |
| RPI | ribose-5-phosphate isomerase |
| TPP | trehalose-6- phosphatase |
| TPS | Trehalose-6-Phosphate synthase. |
Other
| CER | Carbon evolution rate |
| DO | dissolved oxygen |
| IDMS | Isotope dilution mass spectrometry |
| OUR | Oxygen uptake rate |
| PPP | pentose phosphate pathway |
| SRE | Stimulus response experiment |
| TCA | tricarboxylic acid cycle |
| PTM | post translational modification |
| RQ | respiratory quotient. |
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sweere, A.P.J.; Mesters, J.R.; Janse, L.; Luyben, K.C.; Kossen, N.W.F. Experimental simulation of oxygen profiles and their influence on baker’s yeast production: I. One-fermentor system. Biotechnol. Bioeng. 1988, 31, 567–578. [Google Scholar] [CrossRef]
- Larsson, G.; Törnkvist, M.; Wernersson, E.S.; Trägådh, C.; Noorman, H.; Enfors, S.O. Substrate gradients in bioreactors: Origin and consequences. Bioprocess Biosyst. Eng. 1996, 14, 281–289. [Google Scholar]
- Schmalzriedt, S.; Jenne, M.; Mauch, K.; Reuss, M. Integration of physiology and fluid dynamics. Adv. Biochem. Eng. Biotechnol. 2003, 80, 19–68. [Google Scholar]
- De Jonge, L.; Buijs, N.A.A.; Heijnen, J.J.; van Gulik, W.M.; Abate, A.; Wahl, S.A. Flux response of glycolysis and storage metabolism during rapid feast/famine conditions in Penicillium chrysogenum using dynamic 13C labeling. Biotechnol. J. 2014, 9, 372–385. [Google Scholar] [CrossRef]
- Van Kleeff, B.H.A.; Kuenen, J.G.; Heijnen, J.J. Heat flux measurements for the fast monitoring of dynamic responses to glucose additions by yeasts that were subjected to different feeding regimes in continuous culture. Biotechnol. Prog. 1996, 12, 510–518. [Google Scholar] [CrossRef]
- Theobald, U.; Mailinger, W.; Baltes, M.; Rizzi, M.; Reuss, M. In vivo analysis of metabolic dynamics in Saccharomyces cerevisiae: I. Experimental observations. Biotechnol. Bioeng. 1997, 55, 305–316. [Google Scholar] [CrossRef]
- Guillou, V.; Plourde-Owobi, L.; Parrou, J.L.; Goma, G.; François, J. Role of reserve carbohydrates in the growth dynamics of Saccharomyces cerevisiae. FEMS Yeast Res. 2004, 4, 773–787. [Google Scholar] [CrossRef]
- Weber, J.; Kayser, A.; Rinas, U. Metabolic flux analysis of Escherichia coli in glucose-limited continuous culture. II. Dynamic response to famine and feast, activation of the methylglyoxal pathway and oscillatory behaviour. Microbiology 2005, 151, 707–716. [Google Scholar] [CrossRef]
- Mashego, M.R.; van Gulik, W.M.; Vinke, J.L.; Visser, D.; Heijnen, J.J. In vivo kinetics with rapid perturbation experiments in Saccharomyces cerevisiae using a second-generation BioScope. Metab. Eng. 2006, 8, 370–383. [Google Scholar] [CrossRef]
- Buziol, S.; Warth, L.; Magario, I.; Freund, A.; Siemann-Herzberg, M.; Reuss, M. Dynamic response of the expression of hxt1, hxt5 and hxt7 transport proteins in Saccharomyces cerevisiae to perturbations in the extracellular glucose concentration. J. Biotechnol. 2008, 134, 203–210. [Google Scholar] [CrossRef]
- Wahl, S.A.; Nöh, K.; Wiechert, W. 13C labeling experiments at metabolic nonstationary conditions: An exploratory study. BMC Bioinform. 2008. [Google Scholar] [CrossRef]
- Wiechert, W.; Noack, S. Mechanistic pathway modeling for industrial biotechnology: Challenging but worthwhile. Curr. Opin. Biotechnol. 2011, 22, 604–610. [Google Scholar] [CrossRef]
- Kresnowati, M.T.; van Winden, W.A.; Almering, M.J.; ten Pierick, A.; Ras, C.; Knijnenburg, T. A.; Daran-Lapujade, P.; Pronk, J.T.; Heijnen, J.J.; Daran, J.M. When transcriptome meets metabolome: Fast cellular responses of yeast to sudden relief of glucose limitation. Mol. Syst. Biol. 2006. [Google Scholar] [CrossRef]
- Cruz, L.A.B.; Hebly, M.; Duong, G.H.; Wahl, S.A.; Pronk, J.T.; Heijnen, J.J.; Daran-Lapujade, P.; van Gulik, W.M. Similar temperature dependencies of glycolytic enzymes: An evolutionary adaptation to temperature dynamics? BMC Syst. Biol. 2012. [Google Scholar] [CrossRef]
- Bloemen, H.H.J.; Wu, L.; van Gulik, W.M.; Heijnen, J.J.; Verhaegen, M.H.G. Reconstruction of the O2 uptake rate and CO2 evolution rate on a time scale of seconds. AlChE J. 2003, 49, 1895–1908. [Google Scholar] [CrossRef]
- Spanjers, H.; Olsson, G. Modelling of the dissolved oxygen probe response in the improvement of the performance of a continuous respiration meter. Water Res. 1992, 26, 945–954. [Google Scholar] [CrossRef]
- Wu, L.; Lange, H.C.; van Gulik, W.M.; Heijnen, J.J. Determination of in vivo oxygen uptake and carbon dioxide evolution rates from off-gas measurements under highly dynamic conditions. Biotechnol. Bioeng. 2003, 81, 448–458. [Google Scholar] [CrossRef]
- Verheijen, P.J.T. Data Reconciliation and Error Detection. In The Metabolic Pathway Engineering Handbook; Smolke, C., Ed.; CRC Press: Boca Raton, FL, USA, 2010; pp. 8.1–8.13. [Google Scholar]
- Neubauer, P.; Haggstrom, L.; Enfors, S.O. Influence of substrate oscillations on acetate formation and growth yield in Escherichia coli glucose limited fed-batch cultivations. Biotechnol. Bioeng. 1995, 47, 139–146. [Google Scholar] [CrossRef]
- Sonnleitner, B.; Kaeppeli, O. Growth of Saccharomyces cerevisiae is controlled by its limited respiratory capacity: Formulation and verification of a hypothesis. Biotechnol. Bioeng. 1986, 28, 927–937. [Google Scholar]
- Youk, H.; van Oudenaarden, A. Growth landscape formed by perception and import of glucose in yeast. Nature 2009, 462, 875–879. [Google Scholar] [CrossRef] [Green Version]
- Walsh, M.C.; Smits, H.P.; Scholte, M.; van Dam, K. Affinity of glucose transport in Saccharomyces cerevisiae is modulated during growth on glucose. J. Bacteriol. 1994, 176, 953–958. [Google Scholar]
- Van der Rest, M.E.; Kamminga, A.H.; Nakano, A.; Anraku, Y.; Poolman, B.; Konings, W.N. The plasma membrane of Saccharomyces cerevisiae: Structure, function, and biogenesis. Microbiol. Rev. 1995, 59, 304–322. [Google Scholar]
- Van Dijken, J. P.; Weusthuis, R.A.; Pronk, J.T. Kinetics of growth and sugar consumption in yeasts. Antonie Van Leeuwenhoek 1993, 63, 343–352. [Google Scholar] [CrossRef]
- Reifenberger, E.; Boles, E.; Ciriacy, M. Kinetic characterization of individual hexose transporters of Saccharomyces cerevisiae and their relation to the triggering mechanisms of glucose repression. Eur. J. Biochem. 1997, 245, 324–333. [Google Scholar]
- Somsen, O.J.G.; Hoeben, M.A.; Esgalhado, E.; Snoep, J.L.; Visser, D.; van der Heijden, R.T.J.M.; Heijnen, J.J.; Westerhoff, H.V. Glucose and the ATP paradox in yeast. Biochem. J. 2000, 352, 593–599. [Google Scholar] [CrossRef]
- Walther, T.; Novo, M.; Rössger, K.; Létisse, F.; Loret, M.O.; Portais, J.C.; François, J.M. Control of ATP homeostasis during the respiro-fermentative transition in yeast. Mol. Syst. Biol. 2010. [Google Scholar] [CrossRef]
- Aledo, J.C.; Jiménez-Rivérez, S.; Cuesta-Munoz, A.; Romero, J.M. The role of metabolic memory in the ATP paradox and energy homeostasis. FEBS J. 2008, 275, 5332–5342. [Google Scholar] [CrossRef]
- Van halewyn, M.; Dumortier, F.; Debast, G.; Colombo, S.; Ma, P.; Winderickx, J.; van Dijck, P.; Thevelein, J.M. A mutation in Saccharomyces cerevisiae adenylate cyclase, Cyr1(K1876M), specifically affects glucose- and acidification-induced cAMP signaling and not the basal cAMP level. Mol. Microbiol. 1999, 33, 363–376. [Google Scholar] [CrossRef]
- Nasution, U.; van Gulik, W.M.; Proell, A.; van Winden, W.A.; Heijnen, J.J. Generating short-term kinetic responses of primary metabolism of Penicillium chrysogenum through glucose perturbation in the bioscope mini reactor. Metab. Eng. 2006, 8, 395–405. [Google Scholar] [CrossRef]
- Murray, D.B.; Haynes, K.; Tomita, M. Redox regulation in respiring Saccharomyces cerevisiae. Biochim. Biophys. Acta, Gen. Subj. 2011, 1810, 945–958. [Google Scholar] [CrossRef]
- Canelas, A.B.; van Gulik, W.M.; Heijnen, J.J. Determination of the cytosolic free NAD/NADH ratio in Saccharomyces cerevisiae under steady-state and highly dynamic conditions. Biotechnol. Bioeng. 2008, 100, 734–743. [Google Scholar] [CrossRef]
- Aboka, F.O.; Heijnen, J.J.; van Winden, W.A. Dynamic 13C-tracer study of storage carbohydrate pools in aerobic glucose-limited Saccharomyces cerevisiae confirms a rapid steady-state turnover and fast mobilization during a modest stepup in the glucose uptake rate. FEMS Yeast Res. 2009, 9, 191–201. [Google Scholar] [CrossRef]
- Voit, E.O. Biochemical and genomic regulation of the trehalose cycle in yeast: Review of observations and canonical model analysis. J. Theor. Biol. 2003, 223, 55–78. [Google Scholar] [CrossRef]
- Canelas, A.B.; Ras, C.; ten Pierick, A.; van Gulik, W.M.; Heijnen, J.J. An in vivo data-driven framework for classification and quantification of enzyme kinetics and determination of apparent thermodynamic data. Metab. Eng. 2011, 13, 294–306. [Google Scholar] [CrossRef]
- Londesborough, J.; Vuorio, O. Trehalose-6-phosphate synthase/phosphatase complex from bakers’ yeast: Purification of a proteolytically activated form. J. Gen. Microbiol. 1991, 137, 323–330. [Google Scholar] [CrossRef]
- Wilson, W.A.; Roach, P.J.; Montero, M.; Baroja-Fernández, E.; Munoz, F.J.; Eydallin, G.; Viale, A.M.; Pozueta-Romero, J. Regulation of glycogen metabolism in yeast and bacteria. FEMS Microbiol. Rev. 2010, 34, 952–985. [Google Scholar] [Green Version]
- Goldberg, R.N.; Tewari, Y.B.; Bhat, T.N. Thermodynamics of enzyme-catalyzed reactions a database for quantitative biochemistry. Bioinformatics 2004, 20, 2874–2877. [Google Scholar] [CrossRef]
- Canelas, A.B.; ten Pierick, A.; Ras, C.; Seifar, R.M.; van Dam, J.C.; van Gulik, W.M.; Heijnen, J.J. Quantitative evaluation of intracellular metabolite extraction techniques for yeast metabolomics. Anal. Chem. 2009, 81, 7379–7389. [Google Scholar] [CrossRef]
- Cipollina, C.; ten Pierick, A.; Canelas, A.B.; Seifar, R.M.; van Maris, A.J.A.; van Dam, J.C.; Heijnen, J.J. A comprehensive method for the quantification of the non-oxidative pentose phosphate pathway intermediates in Saccharomyces cerevisiae by GC-IDMS. J. Chromatogr. B 2009, 877, 3231–3236. [Google Scholar] [CrossRef]
- Wahl, A.S.; Seifar, R.M.; ten Pierick, A.; Ras, C.; van Dam, J.C.; Heijnen, J.J.; van Gulik, W.M. Quantitative Metabolomics using ID MS; Humana Press: New York, NY, USA, 2013; unpublished work. [Google Scholar]
- Lange, H.C.; Eman, M.; van Zuijlen, G.; Visser, D.; van Dam, J.C.; Frank, J.; de Teixeira Mattos, M.J.; Heijnen, J.J. Improved rapid sampling for in vivo kinetics of intracellular metabolites in Saccharomyces cerevisiae. Biotechnol. Bioeng. 2001, 75, 406–415. [Google Scholar] [CrossRef]
- Douma, R.D.; de Jonge, L.P.; Jonker, C.T.H.; Seifar, R.M.; Heijnen, J.J.; van Gulik, W.M. Intracellular metabolite determination in the presence of extracellular abundance: Application to the penicillin biosynthesis pathway in Penicillium chrysogenum. Biotechnol. Bioeng. 2010, 107, 105–115. [Google Scholar] [CrossRef]
- Wu, L.; Mashego, M.R.; van Dam, J.C.; Proell, A.M.; Vinke, J.L.; Ras, C.; van Winden, W.A.; van Gulik, W.M.; Heijnen, J.J. Quantitative analysis of the microbial metabolome by isotope dilution mass spectrometry using uniformly 13C-labeled cell extracts as internal standards. Anal. Biochem. 2005, 336, 164–171. [Google Scholar] [CrossRef]
- Mashego, M.R.; Wu, L.; van Dam, J.C.; Ras, C.; Vinke, J.L.; Van Winden, W.A.; van Gulik, W.M.; Heijnen, J.J. MIRACLE: Mass Isotopomer Ratio Analysis of U-13C-Labeled Extracts. A New Method for Accurate Quantification of Changes in Concentrations of Intracellular Metabolites. Biotechnol. Bioeng. 2004, 85, 620–628. [Google Scholar] [CrossRef]
- Seifar, R.M.; Ras, C.; van Dam, J.C.; van Gulik, W.M.; Heijnen, J.J.; van Winden, W.A. Simultaneous quantification of free nucleotides in complex biological samples using ion pair reversed phase liquid chromatography isotope dilution tandem mass spectrometry. Anal. Biochem. 2009, 388, 213–219. [Google Scholar] [CrossRef]
- Abate, A.; Hillen, R.C.; Wahl, S.A. Piecewise affine approximations of fluxes and enzyme kinetics from in vivo 13C labeling experiments. Int. J. Robust. Nonlinear Control 2012. [Google Scholar] [CrossRef]
- Rizzi, M.; Baltes, M.; Theobald, U.; Reuss, M. In vivo analysis of metabolic dynamics in Saccharomyces cerevisiae: II. Mathematical model. Biotechnol. Bioeng. 1997, 55, 592–608. [Google Scholar] [CrossRef]
- Heijnen, J.J. Approximative kinetic formats used in metabolic network modeling. Biotechnol. Bioeng. 2005, 91, 534–545. [Google Scholar] [CrossRef]
- Link, H.; Kochanowski, K.; Sauer, U. Systematic identification of allosteric protein-metabolite interactions that control enzyme activity in vivo. Nat. Biotech. 2013, 31, 257–361. [Google Scholar]
Appendix A. Supplementary Information
A.1 Dynamics of Amino Acid Concentrations

© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Suarez-Mendez, C.A.; Sousa, A.; Heijnen, J.J.; Wahl, A. Fast “Feast/Famine” Cycles for Studying Microbial Physiology Under Dynamic Conditions: A Case Study with Saccharomyces cerevisiae. Metabolites 2014, 4, 347-372. https://doi.org/10.3390/metabo4020347
Suarez-Mendez CA, Sousa A, Heijnen JJ, Wahl A. Fast “Feast/Famine” Cycles for Studying Microbial Physiology Under Dynamic Conditions: A Case Study with Saccharomyces cerevisiae. Metabolites. 2014; 4(2):347-372. https://doi.org/10.3390/metabo4020347
Chicago/Turabian StyleSuarez-Mendez, Camilo A., Andre Sousa, Joseph J. Heijnen, and Aljoscha Wahl. 2014. "Fast “Feast/Famine” Cycles for Studying Microbial Physiology Under Dynamic Conditions: A Case Study with Saccharomyces cerevisiae" Metabolites 4, no. 2: 347-372. https://doi.org/10.3390/metabo4020347
APA StyleSuarez-Mendez, C. A., Sousa, A., Heijnen, J. J., & Wahl, A. (2014). Fast “Feast/Famine” Cycles for Studying Microbial Physiology Under Dynamic Conditions: A Case Study with Saccharomyces cerevisiae. Metabolites, 4(2), 347-372. https://doi.org/10.3390/metabo4020347