A Note on (Non)-Locality in Holographic Higher Spin Theories
Abstract
:1. Introduction
2. Definitions of Locality
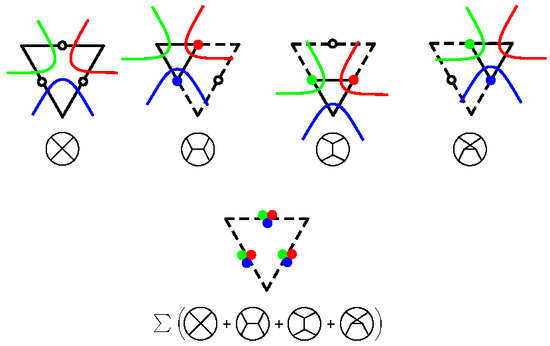
3. Locality in Holographic Higher Spin Theory
4. Mellin Amplitude for the Boundary Correlator
4.1. Inverse Mellin Transform vs. Superposition of Amplitudes
4.2. Regularized Mellin Amplitude
5. Conclusions
Note added:
Acknowledgments
Conflicts of Interest
References
- Weinberg, S. Photons and Gravitons in S Matrix Theory: Derivation of charge conservation and equality of gravitational and inertial mass. Phys. Rev. B 1964, 135, 1049–1056. [Google Scholar] [CrossRef]
- Coleman, S.R.; Mandula, J. All possible symmetries of the S Matrix. Phys. Rev. 1967, 159, 1251–1256. [Google Scholar] [CrossRef]
- Aragone, C.; Deser, S. Consistency problems of hypergravity. Phys. Lett. B 1979, 86, 161–163. [Google Scholar] [CrossRef]
- Metsaev, R.R. Effective Action in String Theory. Ph.D. Thesis, Lebedev Physical Institute, Moscow, Russia, 1991. [Google Scholar]
- Bekaert, X.; Boulanger, N.; Leclercq, S. Strong obstruction of the Berends-Burgers-van Dam spin-3 vertex. J. Phys. A Math. Theor. 2010, 43, 185401. [Google Scholar] [CrossRef]
- Dempster, P.; Tsulaia, M. On the structure of quartic vertices for massless higher spin fields on Minkowski Background. Nucl. Phys. 2012, 865, 353–375. [Google Scholar] [CrossRef]
- Joung, E.; Taronna, M. Cubic-interaction-induced deformations of higher-spin symmetries. J. High Energy Phys. 2014, 2014, 103. [Google Scholar] [CrossRef]
- Ponomarev, D.; Skvortsov, E.D.; (Theoretical Physics Group, Blackett Laboratory, Imperial College London, London, UK). Local obstruction to the minimal gravitational coupling of higher-spin fields in flat space, Unpublished work. 2017.
- Taronna, M. On the non-local obstruction to interacting higher spins in flat space. J. High Energy Phys. 2017, 2017, 26. [Google Scholar] [CrossRef]
- Roiban, R.; Tseytlin, A.A. On four-point interactions in massless higher spin theory in flat space. J. High Energy Phys. 2017, 2017, 139. [Google Scholar] [CrossRef]
- Ponomarev, D.; Skvortsov, E.D. Light-front higher-spin theories in flat space. J. Phys. A Math. Theor. 2017, 50, 095401. [Google Scholar] [CrossRef]
- Ponomarev, D. Chiral higher spin theories and self-duality. arXiv, 2017; arXiv:1710.00270. [Google Scholar]
- Barnich, G.; Henneaux, M. Consistent couplings between fields with a gauge freedom and deformations of the master equation. Phys. Lett. B 1993, 311, 123–129. [Google Scholar] [CrossRef]
- Ponomarev, D. Off-shell spinor-helicity amplitudes from light-cone deformation procedure. J. High Energy Phys. 2016, 2016, 117. [Google Scholar] [CrossRef]
- Sezgin, E.; Sundell, P. Massless higher spins and holography. Nucl. Phys. B 2002, 644, 303–370. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Polyakov, A.M. AdS dual of the critical O(N) vector model. Phys. Lett. B 2002, 550, 213–219. [Google Scholar] [CrossRef]
- Flato, M.; Fronsdal, C. On Dis and Racs. Phys. Lett. B 1980, 97, 236–240. [Google Scholar] [CrossRef]
- Fronsdal, C. Flat Space Singletons. Phys. Rev. D 1987, 35, 1262–1267. [Google Scholar] [CrossRef]
- Sleight, C.; Taronna, M. Higher spin gauge theories and bulk locality: A no-go result. arXiv, 2017; arXiv:1704.07859. [Google Scholar]
- Bekaert, X.; Erdmenger, J.; Ponomarev, D.; Sleight, C. Quartic AdS interactions in higher-spin gravity from conformal field theory. J. High Energy Phys. 2015, 2015, 149. [Google Scholar] [CrossRef]
- Taronna, M. Pseudo-local Theories: A functional class proposal. In Proceedings of the International Workshop on Higher Spin Gauge Theories, Singapore, 4–6 November 2015; World Scientific: Singapore, 2017; pp. 59–84. [Google Scholar]
- Bekaert, X.; Erdmenger, J.; Ponomarev, D.; Sleight, C. Bulk quartic vertices from boundary four-point correlators. In Proceedings of the International Workshop on Higher Spin Gauge Theories, Singapore, 4–6 November 2015; World Scientific: Singapore, 2017; pp. 291–303. [Google Scholar]
- Berends, F.A.; Burgers, G.J.H.; van Dam, H. On the theoretical problems in constructing interactions involving higher spin massless particles. Nucl. Phys. B 1985, 260, 295–322. [Google Scholar] [CrossRef]
- Mack, G. D-independent representation of Conformal Field Theories in D dimensions via transformation to auxiliary Dual Resonance Models. Scalar amplitudes. arXiv, 2009; arXiv:0907.2407. [Google Scholar]
- Mack, G. D-dimensional Conformal Field Theories with anomalous dimensions as Dual Resonance Models. Bulg. J. Phys. 2009, 36, 214–226. [Google Scholar]
- Penedones, J. Writing CFT correlation functions as AdS scattering amplitudes. J. High Energy Phys. 2011, 2011, 25. [Google Scholar] [CrossRef]
- Paulos, M.F. Towards Feynman rules for Mellin amplitudes. J. High Energy Phys. 2011, 2011, 74. [Google Scholar] [CrossRef]
- Fitzpatrick, A.L.; Kaplan, J.; Penedones, J.; Raju, S.; van Rees, B.C. A natural language for AdS/CFT correlators. J. High Energy Phys. 2011, 2011, 95. [Google Scholar] [CrossRef]
- Bekaert, X.; Erdmenger, J.; Ponomarev, D.; Sleight, C. Towards holographic higher-spin interactions: Four-point functions and higher-spin exchange. J. High Energy Phys. 2015, 2015, 170. [Google Scholar] [CrossRef]
- Sleight, C. Interactions in higher-spin gravity: A holographic perspective. J. Phys. A Math. Theor. 2017, 50, 383001. [Google Scholar] [CrossRef]
- Heemskerk, I.; Penedones, J.; Polchinski, J.; Sully, J. Holography from conformal field Theory. J. High Energy Phys. 2009, 2009, 79. [Google Scholar] [CrossRef]
- Hoffmann, L.; Petkou, A.C.; Ruhl, W. Analyticity of AdS scalar exchange graphs in the crossed channel. Phys. Lett. B 2000, 478, 320–326. [Google Scholar] [CrossRef]
- El-Showk, S.; Papadodimas, K. Emergent spacetime and holographic CFTs. J. High Energy Phys. 2012, 2012, 106. [Google Scholar] [CrossRef]
- Liu, H. Scattering in anti-de Sitter space and operator product expansion. Phys. Rev. D 1999, 60, 106005. [Google Scholar] [CrossRef]
- Pappadopulo, D.; Rychkov, S.; Espin, J.; Rattazzi, R. Operator product expansion convergence in conformal field theory. Phys. Rev. D 2012, 86, 105043. [Google Scholar] [CrossRef]
- Rychkov, S.; Yvernay, P. Remarks on the convergence properties of the conformal block expansion. Phys. Lett. B 2016, 753, 682–686. [Google Scholar] [CrossRef]
- Gubser, S.S.; Parikh, S. Geodesic bulk diagrams on the Bruhat-Tits tree. arXiv, 2017; arXiv:1704.01149. [Google Scholar]
- Bertrand, J.; Bertrand, P.; Ovarlez, J.P. Transforms and Applications Handbook; CRC Press: Boca Raton, FL, USA, 2000; Chapter 11. [Google Scholar]
- Gopakumar, R.; Kaviraj, A.; Sen, K.; Sinha, A. Conformal bootstrap in Mellin space. Phys. Rev. Lett. 2017, 118, 081601. [Google Scholar] [CrossRef] [PubMed]
- Rastelli, L.; Zhou, X. How to succeed at holographic correlators without really trying. arXiv, 2017; arXiv:1710.05923. [Google Scholar]
- Paulos, M.F.; Spradlin, M.; Volovich, A. Mellin amplitudes for dual conformal integrals. J. High Energy Phys. 2012, 2012, 72. [Google Scholar] [CrossRef]
- Nandan, D.; Paulos, M.F.; Spradlin, M.; Volovich, A. Star integrals, convolutions and simplices. J. High Energy Phys. 2013, 2013, 105. [Google Scholar] [CrossRef]
- Nizami, A.A.; Rudra, A.; Sarkar, S.; Verma, M. Exploring perturbative conformal field theory in Mellin space. J. High Energy Phys. 2017, 2017, 102. [Google Scholar] [CrossRef]
- Flato, M.; Fronsdal, C. One massless particle equals two dirac singletons: Elementary particles in a curved space. Lett. Math. Phys. 1978, 2, 421–426. [Google Scholar] [CrossRef]
- Joung, E.; Nakach, S.; Tseytlin, A.A. Scalar scattering via conformal higher spin exchange. J. High Energy Phys. 2016, 2016, 125. [Google Scholar] [CrossRef]
- Beccaria, M.; Nakach, S.; Tseytlin, A.A. On triviality of S-matrix in conformal higher spin theory. J. High Energy Phys. 2016, 2016, 34. [Google Scholar] [CrossRef]
- Sleight, C.; Taronna, M. Higher-spin algebras, holography and flat space. J. High Energy Phys. 2017, 2017, 95. [Google Scholar] [CrossRef]
| 1. | Analogous statements can also be proven within the light-cone deformation procedure [14]. |
| 2. | |
| 3. | In the higher spin literature the procedure of perturbative construction of a gauge invariant action, see e.g., [23], is called the Noether procedure. |
| 4. | Primary operators containing one/two trace contractions are called single/double trace operators. For vector models these are bilinear/quadrilinear operators in elementary fields. Conformal blocks with single/double trace operators exchanged are called single/double trace conformal blocks. |
| 5. | An analogous proposal for the Mellin transform for the power law function appeared in the context of the conformal bootstrap in Mellin space [39]. |
| 6. | Instead of (25)–(27) one could split zero into parts, so that each of them has a vanishing arc integral at infinity, which, in turn, ensures that the standard Mellin integral along the imaginary axis can be replaced by the sum of residues. If integration contours for different terms are located so that all singularities except one stay on one side of the contours, then contributions from these singularities cancels out due to the fact that the total reduced Mellin amplitude is vanishing. Then, the only non-vanishing contribution to the amplitude in the coordinate representation is given in terms of residues of the singularity that for different terms appears on different sides of integration contours. Clearly, this contribution will be given by the power function. Some concrete examples of this mechanism at work can be found in [40]. |
| 7. | Four-point exchange diagrams with specially tuned dimensions of the exchanged field and fields on external lines may have a finite sequence of poles in the Mellin amplitude. This happens when the sequence of single trace poles of the reduced Mellin amplitude, e.g., with overlaps with poles of double trace Gamma-functions. In this case all except a finite number of single trace singularities are cancelled in the Mellin amplitude by zeros from . Of course, generic exchanges with fields in the spectrum of the theory should not be regarded as local interactions. This means that for the special values of dimensions of fields as discussed above, locality cannot be defined as a requirement that contact interactions result into Mellin amplitudes with finite sequences of poles. |


© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponomarev, D. A Note on (Non)-Locality in Holographic Higher Spin Theories. Universe 2018, 4, 2. https://doi.org/10.3390/universe4010002
Ponomarev D. A Note on (Non)-Locality in Holographic Higher Spin Theories. Universe. 2018; 4(1):2. https://doi.org/10.3390/universe4010002
Chicago/Turabian StylePonomarev, Dmitry. 2018. "A Note on (Non)-Locality in Holographic Higher Spin Theories" Universe 4, no. 1: 2. https://doi.org/10.3390/universe4010002
APA StylePonomarev, D. (2018). A Note on (Non)-Locality in Holographic Higher Spin Theories. Universe, 4(1), 2. https://doi.org/10.3390/universe4010002