Predicting >10 MeV SEP Events from Solar Flare and Radio Burst Data

Abstract

The prediction of solar energetic particle (SEP) events or solar radiation storms is one of the most important problems in the space weather field. These events may have adverse effects on technology infrastructures and humans in space; they may also irradiate passengers and flight crews in commercial aircraft flying at polar latitudes. This paper explores the use of ≥ M2 solar flares and radio burst observations as proxies for predicting >10 MeV SEP events on Earth. These observations are manifestations of the parent event at the sun associated with the SEP event. As a consequence of processing data at the beginning of the physical process that leads to the radiation storm, the model may provide its predictions with large anticipation. The main advantage of the present approach is that the model analyzes solar data that are updated every 30 min and, as such, it may be operational; however, a disadvantage is that those SEP events associated with strong well-connected flares cannot be predicted. For the period from November 1997 to February 2014, we obtained a probability of detection of 70.2%, a false alarm ratio of 40.2%, and an average anticipation time of 9 h 52 min. In this study, the prediction model was built using decision trees, an interpretable machine learning technique. This approach leads to outputs and results comparable to those derived by the Empirical model for Solar Proton Event Real Time Alert (ESPERTA) model. The obtained decision tree shows that the best criteria to differentiate pre-SEP scenarios and non-pre-SEP scenarios are the peak and integrated flux for soft X-ray flares and the radio type III bursts.

1. Introduction

Solar energetic particle (SEP) events are produced when particles emitted by the Sun are accelerated during a flare or by coronal mass ejection (CME)-driven shocks [1] and reach the Earth along interplanetary magnetic field lines. The associated solar eruptions on the Sun are observed at several wavelengths, including soft X-rays, extreme ultraviolet (EUV), and radio. Energetic protons and ions are the main constituents of SEP events, and their effects are more severe than other particles, such as electrons. In space, SEP events may pose a significantly high risk of cancer to astronauts and damage a spacecraft’s electronic components [2,3,4,5]. On Earth, SEPs may irradiate passengers and flight crews in aircraft flying at polar latitudes [6,7,8].

In this paper, SEP events refer to the detection of high fluxes of energetic protons and ions in the near-Earth environment. Forecasting SEP events helps to improve mitigation of the aforementioned adverse effects. The prediction of SEP events is a challenge not only because these events are complex physical processes, the physics of which is still under study, but also because they are rare events. Indeed, in the period 2007–2020, only 42 SEP events were detected by the Geostationary Operational Environmental Satellite (GOES) satellites (J (E > 10 MeV) >10 proton flux units (pfu)).

The objective of this work is to predict the occurrence of SEP events with energies >10 MeV from flare and radio burst data. This study explores the use of an interpretable machine learning technique to predict >10 MeV SEP events from National Oceanic and Atmospheric Administration/Space Weather Prediction Center (NOAA/SWPC) data files, which may be easily obtained online. The final purpose of the model, called the University of Malaga predictor from Solar Data (UMASOD), is to optimize the probability of detection (POD), false alarm ratio (FAR), and average warning time (AWT). The first two metrics are optimized by maximizing the critical success index (CSI), which is used in atmospheric meteorology to assess severe weather predictors, providing a way to combine POD and FAR in a single value. Regarding the anticipation time (i.e., AWT), we approach it using flare data and radio burst data which are observational data at the beginning of the physical process.

Other approaches have also been proposed to analyze solar flare and radio data to predict the occurrence of >10 MeV SEP events [9,10,11]. In this paper, we call these approaches radio-data-based SEP event predictors. We compare our forecasting results with those obtained by the Empirical model for Solar Proton Event Real Time Alert (ESPERTA) model [10,11], which is the cutting edge in radio-data-based SEP event predictors. Currently, ESPERTA is not in operation because the radio data on which it depends are not available in real time.

Machine learning is a set of techniques for discovering knowledge and correlations from data with several purposes. These techniques have been used for the identification of patterns in datasets, employing several different tasks such as classification, regression, and summarization, among others. In the field of SEP event predictions, several machine learning techniques have been used. For example, Winter and Ledbetter [1] employed principal component analysis (PCA) to show that solar flare and radio burst data can lead to effective >10 MeV SEP prognosis. Boubrahimi et al. [12] used interpretable decision tree (DT) models for predicting >100 MeV SEP events from solar soft X-ray (SXR) and in situ proton observations. In this study, we also use interpretable DT models for predicting >10 MeV SEP events from solar flare and radio burst data.

This paper is organized as follows: Section 2 describes the problem to solve, including a brief explanation about solar proton events, flares, and radio bursts. Section 3 describes our approach to constructing the prediction model. Section 4 discusses the results and compares them with those obtained by other similar approaches, and Section 5 presents the conclusions.

2. Description of the Problem

During a strong solar eruption, a flare and a CME take place. Solar eruptions are monitored using soft X-rays and radio data. A solar eruption may lead (with a low probability) to the occurrence of solar radiation storm in the near-Earth environment.

In this section, we present a brief description of these phenomena and the relation between them.

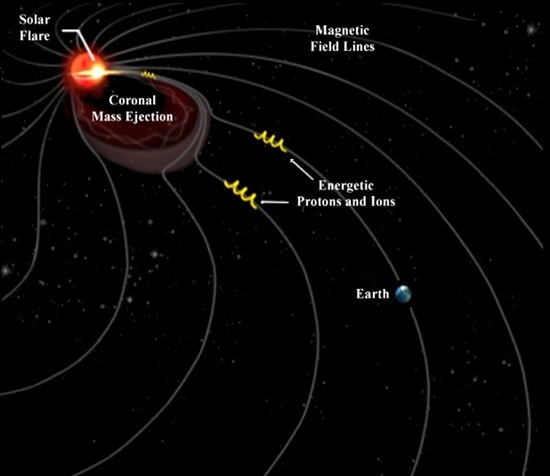
2.1. SEP Events

It is known that the frequency of SEP events varies, following a periodic 11year cycle of solar activity. In Figure 1, the evolution of the number of sunspots is shown, and the solar cycles can be clearly observed. It is important to learn prediction knowledge from a variety of solar and interplanetary situations; for this reason, in this study we used events from 1997 to 2014, which covered the entire 23rd solar cycle and part of the 24th cycle.

SEPs are accompanied by other phenomena like flares and radio bursts, which are discussed below.

2.2. Solar Flares

A solar flare is a sudden brightening in the solar atmosphere, typically spread across all atmospheric layers and involving substantial mass motions and particle acceleration. A solar flare occurs when magnetic energy in the solar atmosphere is suddenly released.

Solar flares can be described using various parameters such as heliolongitude and heliolatitude, brightness, area, and X-ray flux. Solar flares are classified into five classes (A, B, C, M, X), according to the peak flux of the soft X-rays, with the X-class flares being the most intense ones. Within each class, a number is put to indicate the intensity (e.g., an M1 flare is less intense than an M2 flare). Like ESPERTA [10,11], our model is triggered by ≥M2 flares to predict >10 MeV SEP events.

2.3. Radio Bursts

The research on solar radio bursts provides considerable possibilities for the study of some important pre-phenomena in solar physics. It is important to separate fixed-frequency radio bursts and sweep-frequency radio bursts. The first analysis type only considers some discrete frequencies and measures the peak values of microwaves at these frequencies; moreover, they were used before to predict SEPs with good results [13]. Regarding the shape of the radio burst, some different types of sweep-frequency radio bursts can be distinguished.

Although there is a larger number of solar radio burst types, types II to IV are briefly introduced below as they are known to be related to pre-SEP scenarios.

• Type II:

These bursts are indications of the shock acceleration of electrons. They typically occur at around the time of the SXR flux peak in a solar flare, when the CME has already erupted and there is a shock. They drift slowly in frequency and last between a few minutes and half an hour, with a frequency range of approximately 50 to 120 MHz [13,14,15,16,17].

• Type III:

Type III bursts are produced by electron beams traveling outward throughout the corona and interplanetary space. They are brief radio bursts that drift very rapidly in frequency versus time. They occur over a frequency range of 10 kHz to 8GHz and are associated with flares, although not every flare is accompanied by a type III burst. Although not as frequent, type III bursts may also travel inward, toward the solar surface [14,15,16,17,18,19].

• Type IV:

The broadband and non-drifting nature of type IV emission has led to the widespread belief that they are due to trapped electrons in closed magnetic structures, which could be low in the corona during flares, or trapped electrons in a CME directed toward Earth. They are indications that very energetic electrons are forced to turn and, thus, have not escaped, but there is an intense electron activity. Type IV bursts are broadband quasi-continuum features associated with the decay phase of solar flares. These radio bursts are also nearly always associated with large flares of long duration. There are also drifting cases which could indicate that electrons escape. Type IV bursts are also associated with type II bursts [13,15,16,17].

Current association between SEPs and radio bursts:

Solar radio bursts were connected in past studies to energetic particles in general and SEP events in particular [5,8,15,16,17,18,19,20,21,22,23]. In brief, the currently accepted role of radio bursts in SEP predictions may be summarized as follows: there is a high association between SEP events and type III bursts (electron escape) during the first phase of solar eruptions, followed by type II (shock-accelerated electrons in the interplanetary medium) and IV (trapped electrons in a magnetic structure, e.g., a traveling CME).

It is important to mention that the radio emissions are only due to electrons. However, like ESPERTA, our model associates remote SXR and radio signatures with in situ protons, despite the fact that there is no direct cause–effect association. A current empirical association [21,24] is that if there is evidence that electrons were accelerated and could escape, then it is also probable that protons could also be accelerated and escape.

Table 1. Dominant features of different type of solar radio bursts.

Type	Features	Duration	Frequency Range	Associated Phenomena
II	Slow-frequency drift bursts	3–30 min	20–150 MHz	Shock-accelerated electrons
III	Fast-frequency drift bursts	Burst: 1–3 s Group: 1–5 min Storm: minutes–hours	10 kHz–1 GHz	Electron escape
IV	Broadband continuum	Hours to Days	20 MHz–2 GHz	Trapped electrons

shows a compilation of the characteristics and associated phenomena of these bursts. Moreover, the information about the NOAA edited event files [25] describes the remaining bursts types (V, VI, VII, and broadband long-lived dekametric continuum (CTM)) which are not explained here because, in Section 4, they were found to be irrelevant for predicting SEP events.

3. Methodology

The purpose of the proposed UMASOD model is to process the NOAA/SWPC Solar Edited Event file to build a decision tree that predicts >10 MeV SEP events. In order to obtain the training examples, we took two data sources. We used the SWPC Solar Event list [25] provided by the NOAA to build the unlabeled training examples; then, each of these examples were labeled with either “an SEP event is expected” or “no SEP event is expected” using the SEP list [26] provided by NASA and NOAA with the SEPs detected on Earth. During real-time operations, the final model should be able to use the analysis of the NOAA/SWPC Solar Edited Event file to predict >10 MeV SEP events. These files are updated every 30 min at 2 and 32 min past the hour.

The first data source, i.e., the NOAA/SWPC Solar Edited Event files, includes all the information about a great number of solar phenomena such as flares, CMEs, and radio bursts. Each file includes specific information about each type of phenomenon and a solar eruption code. Our pre-processing program gets the information on radio bursts, flares, and X-Rays, and saves it in an event list, called here the “Solar Event List”, which is used as the training dataset. An SEP event is associated with a single solar eruption code. A solar eruption is a complex process that is associated with several solar events (e.g., a flare, a radio burst); for this reason, several solar events may share the same (solar eruption) code.

The second source, the NOAA/NASA SEP list, is used only during the training phase. This list provides information about the intensity of SEP events, as well as information about the associated solar flare.

Both sources, the SWPC event list and the SEP list, provide flare time, peak, and location data, which are used to associate the data in both lists. Thus, for the period 1997–2014, our pre-processing program successfully associated 96 of the 98 SEPs (with full information) with an event from the event list. The information on the SEPs was added to the related solar events, and then filtered, taking into account only the events with a flare peak ≥M2, i.e., the filtering criterion used by the ESPERTA model [10,11]. The obtained event list contained a high proportion of negative instances.

3.1. Pre-Processing Events from NOAA/NASA Files

The first step in this study consisted of reading all the information provided in the NOAA files. Two different types of files were used.

Firstly, the NOAA edited event list [25] includes all the information related to flares, X-rays, coronal mass ejections, and radio bursts. Since 1997, this event list file has been edited daily and information is updated every 30 min. The file specifies the following information for each of these phenomena:

• An event ID, which identifies the different phenomena that are associated with the same event, as well as the beginning and end of the phenomenon. It also includes the peak time for some of them.
• The observatory that measured the phenomena, from a list of seven observatories in the USA, Australia, and Italy. The quality of the measurements is also presented.
• The type of phenomenon, which includes all the phenomena previously cited, and others that are not relevant for this work. There is also specific information, depending on the type. This is explained later.
• The assigned solar region number.

Our pre-processing program recorded a total of 89,002 different events from 1997 to 2014.

Secondly, the NOAA/NASA SEP list [26] includes all the information on SEP events since 1976. The following data are shown for every SEP event:

• Start and peak time of the event, and maximum proton flux.
• Associated CME, only since 1997.
• Associated flare, including the time when the peak of the flare was produced, the importance of the flare, the location in heliolatitude and heliolongitude, and the region.

The program recorded a total of 98 SEP events from 1997 to February 2014.

Firstly, our pre-processing program read the edited event list files from 1997 to 2014. The data were stored in our Solar Event List, which contained the following properties:

• ID of the event,
• Date of the event,
• Peak value of the flare taken from X-ray information, if it exists,
• Start, end, and peak times, also taken from X-ray information,
• The location of the flare in solar coordinates,
• Intensity, frequency range, duration, and rise time for each of the different types of sweep-frequency radio bursts included in the edited event list. The frequency range of the radio sweep bursts was 25–180 MHz.

Secondly, the program read the mentioned NOAA/NASA SEP list file. The program recorded the information of all the SEPs from 1997 to February 2014 in another list, called here the “Storm List”, which contained all the fields mentioned above except for the associated CME and the region of the flare. There were a total of 125 SEPs during this period, but only 98 of them had information in all the fields.

3.2. Associating Events

Events from both lists (i.e., the Solar Event List and the Storm List) were associated. The procedure was as follows. Firstly, for each SEP in the Storm List, the program checked if it had information in all fields. If so, the program searched the Solar Event List for those events that happened within the prior 24 h of the occurrence of the SEP event. Then, from those events, the peak value of the flare was compared with the peak value of the associated flare of the SEP event. If there was more than one event with the same peak within the prior 24 h, the program looked for the coordinates of the flare and took the closer one to the associated flare coordinates.

After this process, 96 of the 98 SEP events mentioned above were successfully related to items in the Solar Event List. The two remaining SEPs were the event of 4 November 2003, because there was no event with the same peak value that day, and the event of 6 January 2014, because there was no event file from the NOAA for that day. Both events were excluded.

The information from the Storm List was saved into the associated events in the Solar Event List, and a Boolean property in the solar event was changed to the true class (i.e., “an SEP event is expected”), indicating that it produced an SEP event; otherwise, the solar event was labeled with the false class (i.e., “no SEP event is expected”).

3.3. Filtering Events

The next step involved filtering both positive events, i.e., those with an associated SEP, and negative events, mainly according to their X-ray peak.

These filters were applied in two steps. In the first place, all events that contained neither an SEP event nor a sweep-frequency radio burst (I–VII) were discarded. The remaining events were filtered as a function of their X-ray peak, discarding all events below M2. Since the M2 threshold worked properly for the ESPERTA model [10,11], we used it in our approach.

After this process, only 75 out of 96 SEP events passed the filter. However, the Solar Event List went from the previously mentioned 89,002 events to only 502. This means that there were 75 positive instances, i.e., solar events whose class was true (i.e., an SEP took place after the event was observed on the Sun), and 427 negative ones.

Table 2. List of events used in machine learning.

Date	Proton Flux (pfu)	Flare Peak	Flare Location
4 November 1997	72	X2	S14W33
6 November 1997	490	X9	S18W63
2 May 1998	150	X1	S15W15
6 May 1998	210	X2	S11W65
24 August 1998	670	X1	N30E07
25 September 1998	44	M7	N18E09
30 September 1998	1200	M2	N23W81
23 January 1999	14	M5	N27E90
5 May 1999	14	M4	N15E32
4 June 1999	64	M3	N17W69
7 June 2000	84	X2	N20E18
10 June 2000	46	M5	N22W38
14 July 2000	24,000	X5	N22W07
22 July 2000	17	M3	N14W56
16 October 2000	15	M2	N04W90
8 November 2000	14,800	M7	N05W77
24 November 2000	940	X2	N20W05
29 March 2001	35	X1	N14W12
2 April 2001	1110	X20	N18W82
10 April 2001	355	X2	S23W09
15 April 2001	951	X14	S20W85
28 April 2001	57	M7	N17W31
24 September 2001	12,900	X2	S16E23
1 October 2001	2360	M9	S22W91
19 October 2001	11	X1	N15W29
22 October 2001	24	X1	S18E16
4 November 2001	31,700	X1	N06W18
19 November 2001	34	M2	S13E42
22 November 2001	18,900	M9	S15W34
26 December 2001	779	M7	N08W54
29 December 2001	76	X3	S26E90
20 February 2002	13	M5	N12W72
17 March 2002	13	M2	S08W03
17 April 2002	24	M2	S14W34
21 April 2002	2520	X1	S14W84
16 July 2002	234	X3	N19W01
14 August 2002	26	M2	N09W54
22 August 2002	36	M5	S07W62
24 August 2002	317	X3	S08W90
9 November 2002	404	M4	S12W29
28 May 2003	121	X3	S07W17
31 May 2003	27	M9	S07W65
18 June 2003	24	M6	S08E61
26 October 2003	466	X1	N02W38
28 October 2003	29,500	X17	S16E08
21 November 2003	13	M5	N02W17
13 September 2004	273	M4	N04E42
7 November 2004	495	X2	N09W17
16 January 2005	5040	X2	N15W05
14 May 2005	3140	M8	N12E11
16 June 2005	44	M4	N09W87
14 July 2005	134	M5	N10W80
27 July 2005	41	M3	N11E90
22 August 2005	330	M5	S12W60
8 September 2005	1880	X17	S06E89
6 December 2006	1980	X9	S07E79
13 December 2006	698	X3	S05W23
8 March 2011	50	M3	N24W59
7 June 2011	72	M2	S21W64
4 August 2011	96	M9	N15W49
9 August 2011	26	X6	N17W83
23 September 2011	35	X1	N11E74
23 January 2012	6310	M8	N28W36
27 January 2012	796	X1	N27W71
7 March 2012	6530	X5	N17E15
13 March 2012	469	M7	N18W62
17 May 2012	255	M5	N12W89
7 July 2012	25	X1	S18W50
12 July 2012	96	X1	S16W09
11 April 2013	114	M6	N09E12
14 May 2013	41	X1	N11E51
22 May 2013	1660	M5	N15W70
23 June 2013	14	M2	S16E66
20 February 2014	22	M3	S15W67
25 February 2014	103	X4	S12E82

shows a compilation of all SEP events that passed the filter.

3.4. Usability of the Radio Burst Information

Up to now, the obtained events list contains the information of the seven sweep-frequency radio burst types, but it is possible that part of this information cannot be used for predicting an SEP event.

In general, a real-time SEP occurrence prediction model should issue the predictions before the start time of the SEP events (e.g., the time at which the >10 MeV integral proton flux surpasses 10 pfu). Therefore, such models have to be trained only with information that is available before the start time of the SEP events. That is, any datum that is not available before the SEP event start time is not useful for real-time prediction purposes; thus, it should be discarded from the training and testing phases. For example, if a radio burst ends after the start time of the SEP event, it is not possible to use the information of the radio burst to predict the SEP. Therefore, to know which radio bursts are useful for making real-time SEP occurrence predictions, the pre-processing program generates a table that contains, for each SEP event, the lists of differences in minutes between the end time of each type of sweep-frequency radio burst (RSP) and the SEP start time. This information is shown in

Table 3. Time differences in minutes from the end of the RSP to the start of the solar energetic particle (SEP) events for the period 1997–2014.

Date	SEP	Flare Location	RSP II (min)	RSP III (min)	RSP IV (min)	RSP V (min)
4 November 1997	X2.1	S14W33	139	139	−109	136
6 November 1997	X9.4	S18W63	-	-	−654	-
2 May 1998	X1.1	S15W15	-	-	−541	-
6 May 1998	X2.7	S11W65	-	-	−54	-
24 August 1998	X1.0	N35E09	−5	110	−5	-
25 September 1998	M7.1	N18E09	2465	2447	2288	-
30 September 1998	M2.8	N23W81	110	-	73	125
23 January 1999	M5.2	N27E90	3822	-	3801	3810
5 May 1999	M4.4	N15E32	3614	-	3551	-
4 June 1999	M3.9	N17W69	-	-	117	-
7 June 2000	X2.3	N20E18	1316	1346	974	-
10 June 2000	M5.2	N22W38	47	66	-	-
14 July 2000	X5.7	N22W07	19	-	−431	-
22 July 2000	M3.7	N14W56	99	-	−271	-
16 October 2000	M2.5	N04W90	247	265	−755	-
8 November 2000	M7.4	N10W77	-	42	20	-
24 November 2000	X2.0	N20W05	591	-	-	-
29 March 2001	X1.7	N20W19	-	387	-	-
2 April 2001	X20	N18W82	103	107	-	-
10 April 2001	X2.3	S23W09	213	200	−357	-
15 April 2001	X14.4	S20W85	15	24	−55	-
28 April 2001	M7.8	N17W31	2331	2360	1756	-
24 September 2001	X2.6	S16E23	-	163	−495	-
1 October 2001	M9.1	S22W91	-	380	-	-
19 October 2001	X1.6	N15W29	343	-	321	-
22 October 2001	X1.2	S18E16	60	71	-	-
4 November 2001	X1.0	N06W18	44	-	−105	-
19 November 2001	M2.8	S13E42	3335	-	3005	-
22 November 2001	M9.9	S15W34	39	-	−280	-
26 December 2001	M7.1	N08W54	46	-	−457	-
29 December 2001	X3.4	S26E90	510	-	-	-
20 February 2002	M5.1	N12W72	62	93	53	92
17 March 2002	M2.2	S08W03	-	-	1895	-
17 April 2002	M2.6	S14W34	427	426	−62	-
21 April 2002	X1.5	S14W84	55	63	−20	-
16 July 2002	X3.0	N19W01	-	1304	1070	-
14 August 2002	M2.3	N09W54	412	421	-	415
22 August 2002	M5.4	S07W62	158	165	-	-
24 August 2002	X3.1	S02W81	26	37	4	-
9 November 2002	M4.6	S12W29	343	-	327	-
28 May 2003	X3.6	S07W17	1382	1388	1254	-
31 May 2003	M9.3	S07W65	127	-	-	133
18 June 2003	M6.8	S08E61	1312	1326	1250	-
26 October 2003	X1.2	N02W38	42	-	-	-
28 October 2003	X17.2	S16E08	64	-	−196	-
21 November 2003	M5.8	N02W17	-	1441	-	-
13 September 2004	M4.8	N04E42	2656	2648	2615	-
7 November 2004	X2.0	N09W17	174	-	−889	-
16 January 2005	X2.6	N14W08	192	-	−502	-
14 May 2005	M8.0	N12E12	753	764	508	-
16 June 2005	M4.0	N09W87	104	118	93	-
14 July 2005	M5.0	N11W90	-	754	-	756
27 July 2005	M3.7	N11E90	1077	-	-	-
22 August 2005	M5.6	S12W60	-	-	−65	-
8 September 2005	X17.0	S06E89	505	-	449	-
6 December 2006	X9.0	S07E79	1756	1761	1741	-
13 December 2006	X3.4	S06W24	35	29	−1250	-
8 March 2011	M3.7	N24W59	290	-	-	-
7 June 2011	M2.5	S21W54	90	-	82	-
4 August 2011	M9.3	N19W36	152	162	-	154
9 August 2011	X6.9	N17W69	29	-	-	-
23 September 2011	X1.4	N11E74	2170	-	-	-
23 January 2012	M8.7	N28W21	-	-	−211	-
27 January 2012	X1.7	N27W71	40	-	21	-
7 March 2012	X5.4	N17E27	279	-	−320	291
13 March 2012	M7.9	N18W62	-	-	-	-
17 May 2012	M5.1	N11W76	29	33	−42	-
7 July 2012	X1.1	S18W50	279	293	-	291
12 July 2012	X1.4	S15W01	102	-	−324	-
11 April 2013	M6.5	N09E12	226	215	−377	-
15 May 2013	X1.2	N12E64	700	-	697	-
22 May 2013	M5.0	N15W70	75	-	30	-
23 June 2013	M2.9	S16E73	-	3903	3878	-
20 February 2014	M3.0	S15W73	53	71	-	79
25 February 2014	X4.9	S12E82	773	785	741	-

. Since a single event does not contain all types of radio bursts, the table shows a “-” if the event does not contain that particular type. We must note that the event of 24 August 1998 contained an anomalous date for the radio burst types II and IV, and these radio bursts took place before the SEPs.

As can be seen in

Table 4. Percentage of RSPs occurring after the SEP.

Type	Number of RSPs	After the SEP	Percentage
II	59	0	0.00%
III	38	0	0.00%
IV	54	25	46.30%
V	11	0	0.00%

, the end of the sweep-frequency radio bursts of type IV is very likely to take place after the start of the SEP event, and type V is related to a low percentage of SEP events. Because of that, these types of radio bursts were excluded hereinafter from the generation of the model.

Table 4 shows the number of radio bursts that ended before the start of the SEP event in relation to the number of radio bursts of each type.

3.5. Preparing Instances for the Machine Learning

Before starting the generation of the prediction model, it was necessary to calculate some new variables as a combination of others or to discretize some continuous attributes.

Firstly, the program discretized the location of the flare of the event; to be able to do this, it was necessary to obtain the heliolongitude and heliolatitude from the location string of the form “N30W40”. The heliolatitude takes an integer value from −90 (S90 i.e., south 90) to +90 (N90 i.e., north 90), while the heliolongitude can take values below 90 (W90 i.e., west 90) and over −90 (E90 i.e., east 90), if the flare is produced on the back side of the Sun. Then, the program saved a discretization of these values in the variables Discrete Heliolongitude, and Discrete Heliolatitude, dividing each coordinate into 12 regions.

Secondly, the SXR peak was saved as the logarithm of the soft X-ray peak flux with flare classes of C, M, and X, meaning 10⁻⁶, 10⁻⁵, and 10⁻⁴ Watts/m², respectively; for example, a value of X2.5 means an SXR flux of 2.5 × 10⁻⁴ Watts/m². In this way, the classes followed a linear progression instead of an exponential progression. The program also discretized the logarithm value, dividing the scale into 22 sections, and saving it if the logarithm was greater than each one of the 21 points of divisions (e.g., SXR ≥ X2.5). This information was stored in a Boolean array.

Thirdly, the program also calculated the duration and rise time, in minutes, of the flare and each of the radio bursts, saving this information in the events.

Lastly, the program calculated the approximate integrals of each of the sweep-frequency radio burst fluxes for each event. To calculate these approximate integrals, it simply multiplied the intensity of the radio burst and the duration of the phenomenon in minutes. This information was stored inside the event. Then, following the example of Laurenza [10], who multiplied the integral of X-rays and the integral of microwave to predict the occurrence of SEP events, the program calculated the product of the integral of X-rays and radio bursts of types II and III, which were the most common radio types. It was necessary to calculate 10 thresholds for each type. These thresholds were the percentiles 0, 10, 20, etc. of the products of the integral of each event with a related SEP event. The program stored, in two Boolean arrays, whether the products of the integrals of X-ray and radio bursts of types II and III exceeded their respective thresholds.

All this information, together with the previous data from NOAA/NASA files, was exported to a CSV file containing the values of the attributes of the 502 events mentioned, as well as a Boolean class, which was true if there was an SEP event and false otherwise.

3.6. Generating the Prediction Model

As explained above, the class was imbalanced, with 75 positive events and 427 negative ones, i.e., a 15%/85% proportion. Training datasets with imbalanced class distribution are an important problem in machine learning [27]. The main approaches to this issue are sampling methods, cost-sensitive methods, and instance-weighting methods.

The first involves the modification of the dataset via various mechanisms to provide a balanced distribution [28]. This can be made via oversampling, i.e., adding copies of the minority class, or under-sampling, i.e., removing copies of the majority class.

The second considers the costs associated with misclassifying examples and applies a different cost from cost matrices to each data example as a function of its class value [29].

The third weights the instances in the data such that each class has the same total weight, maintaining the total sum of weights across all instances [30].

These three methods were compared and there was no clear winner [31] among them regarding performance. This paper used the instance-weighting approach implemented in Weka via the ClassBalancer Filter [32].

For the generation of the decision tree, the J48 algorithm was used [33]. We developed a program that uses the Weka API [34] to try different values of the minimum number of instances per leaf to generate the model, evaluating them by 20-fold cross-validation. With the minimum number of instances per leaf, the program generates a model and evaluates it by cross-validation, thereby optimizing the POD and FAR of the model. We carried out the optimization approach described in Section 3.7.

The errors obtained here were errors of generalization, i.e., the error calculated using a testing set whose examples were not included in the training set. POD and FAR are two frequently used metrics in the prediction of SEP events. POD is the number of SEPs correctly classified compared to the total number of SEP events occurred. FAR is the number of false alarms compared to the number of false alarms plus the number of SEPs correctly classified.

3.7. Optimization of the Decision Tree

Usually, there are two event-oriented prediction performance metrics that can be used for the optimization of the decision tree: receiver operating characteristic [35] area under the curve (ROC-AUC) and precision recall area under the curve (PR-AUC) [36]. There is an additional event-oriented prediction performance metric, mostly used by atmospheric weather experts, called the critical success index (CSI) [37], which can also be applied for optimization purposes.

Regarding the ROC-AUC approach, an ROC curve is the plot of the true positive rate (TPR) against the false positive rate (FPR). The TPR is defined as TPR = TP/(TP + FN), and the FPR is defined as FPR = FP/(FP + TN), where TP = true positive, TN = true negative, FP = false positive, and FN = false negative. The goal of the ROC-AUC is to have the model be at the upper left corner. A higher area under the ROC curve denotes a better model. In order to use this approach, we used a 20-fold cross-validation, varying the minimum number of instances per leaf. Figure 2 shows the area under the curve as a function of the minimum number of instances per leaf. As seen, taking into account the ROC-AUC approach, the best number of instances per leak was 17. By using the 20-fold cross-validation on the training and validation sets of solar events (i.e., associated with ≥M2 flares) and the ROC-AUC optimization approach, the obtained POD was 80% (60/75) and the FAR was 61.54% (96/156).

When being confronted with the class imbalance problem [27,28], the TN count (i.e., true negative) was too large, providing an FPR that was too low in all predictors. For this reason, ROC-AUC analysis [35] did not provide useful comparative results among predictors, which is why the PR-AUC [36] and the CSI approach [37] were used. Regarding the PR-AUC approach, the PR curve plots precision against recall. Precision is defined as TP/(TP+FP), and recall is defined as TP/(TP+FN). Note that recall is POD and precision is 1 − FAR. In the case of the PR-AUC, the goal is to have the model be at the upper right corner, which basically represents only true positives with no false positives and no false negatives. The precision recall area under curve (PR-AUC) is just the area under the PR curve. According to this approach, a higher value denotes a better model. The main difference between the ROC-AUC and PR-AUC is that the PR does not account for true negatives (as TN is not a component of either precision or recall). The PR-AUC approach uses a combination of POD and 1 − FAR. Note that there is no single way to combine POD and FAR.

In this study, we used the CSI to optimize the POD and FAR. CSI is a metric that proved its utility after decades of use by atmospheric weather experts. The US National Weather Service uses this measure to assess predictors because, according to them [37], it is an unbiased verification statistic appropriate for predicting rare events, and, for this reason, it is used to assess severe weather predictors. CSI has also been used in SEP event prediction modeling for optimizing POD and FAR [38,39,40]. The CSI combines POD and FAR as follows: CSI = (POD⁻¹ + (1 − FAR)⁻¹ − 1)⁻¹. An CSI of 100% is the indication of an excellent predictor with POD= 100% and FAR= 0%. In order to optimize our model using CSI, we used a 20-fold cross-validation evaluation over the training and testing cases, varying the minimum number of instances per leaf. For each cross-validation, we obtained the POD and FAR, which were used for calculating the CSI.

Figure 3 presents the CSI index as a function of the minimum number of instances in the leaf. Taking into account the CSI, the best number of instances per leaf was eight. By using the 20-fold cross-validation on training and validation sets of solar events (i.e., associated with ≥M2 flares) and the application of the CSI optimization approach, the obtained POD was 85.3% (64/75) and the FAR was 54.6% (77/141).

Note that the resulting POD using ROC-AU analysis was the same as that using the CSI-based approach, but the FAR was better (54.6% vs. 61.54%) using the CSI-based approach, mainly because it is only driven by the optimization of POD and FAR, and the ROC analysis is not.

3.8. Analysis of Variable in the Decision Tree

The final predictive decision tree (see Figure 4) was constructed using the J48 method with the Weka tool [34] and the optimization approach, explained in Section 3.7. Note that the first node of the tree is actually the filtering of the <M2 flares that we performed, as our model only considered events associated with flares ≥M2. The rest of the tree corresponds to the model generated by Weka.

As can be seen, the most important attribute was the integral of SXR fluxes. This tree also shows that a flare’s heliolatitude and the maximum frequency of radio type III (i.e., the signature of the electron escape) were also important for differentiating a pre-SEP scenario from a non-pre-SEP scenario. Three additional important attributes were the logarithm of the flare SXR peak, the flare rise time, and “SXR ×type III 9”, which was the product of integrals of SXR flux and type III radio bursts of discrete range 9. The latter factor is the main prediction condition in the ESPERTA system [10,11].

It is interesting to note that type II radio bursts were excluded by the machine learning (J48) algorithm in Section 3.7; this means that this learning algorithm found better correlations to predict SEPs than the occurrence of type IIs. On the other hand, according to the analysis made in Section 3.4, type IVs were also excluded because the end of these sweep-frequency radio bursts was very likely to take place after the start of the SEP event, and type Vs were excluded because of the low probability of them taking place before the start of SEP events.

4. Results and Discussion

This section evaluates the performance of the final decision tree (shown in Figure 4) in predicting the >10 MeV SEP events associated with flares (called here flare-associated SEPs). There were 104 such events from 1997 to February 2014.

Since the number of <M2 flares was larger than the number of ≥M2 flares, we noted that the prediction of flare-associated SEPs using all flares without filtering generated a much larger FAR than that presented in Section 3.7, which did not allow us to make a proper optimization. For this reason, we decided to construct a predictor of ≥M2 flare SEPs to finally use it for the prediction of all flare-associated SEPs.

In the field of machine learning, models are evaluated with a dataset that is different than the training set. These results are presented in Section 3.7. In the field of solar radiation prediction, the forecasting performance is also presented, evaluating all available SEP events (including those used for training) because the number of solar storms was very reduced; thus, little data were available in order to learn to predict events in this complex problem. For this reason, in order to compare our performance with other approaches, in this section, we used the decision tree in Figure 4, built in Section 3.7, to predict the 104 flare-associated SEP events.

Table 5. Comparison of results of the different models. UMASOD, University of Malaga predictor from Solar Data; POD, probability of detection (POD); FAR, false alarm ratio; AWT, average warning time.

Model	Period	POD	FAR	AWT
UMASOD	1997–2014 (a)	70.2% (73/104)	40.2% (49/122)	9 h 52 min
ESPERTA	1995–2014 (b)	62% (66/107)	39% (42/108)	~9 h
ESPERTA	1995–2005 (a)	63% (47/75)	42% (34/81)	~9 h
UMASEP-10 (vers2.0)	1997–2014 (a)	93.3% (70/75)	25.5% (24/94)	4 h 01 min

(a) Model trained and evaluated with the same data; (b) model trained using 1995–2005 data, evaluated with 1995–2014 data.

compares the results obtained by our model UMASOD for the period 1997–2014, with those of the ESPERTA model [10,11,41], which used two evaluation periods 1995–2005 and 1995–2014 and different training/testing conditions. For the case of UMASOD, the AWT was calculated by simulating real-time operations, i.e., we took the time of the most delayed solar event end time (radio burst or flare), and we added the delay for SWPC to collect the solar event information and update the edited event list file [25], which is currently 30 min, but which will surely be reduced when using more automated methods. In general, it can be seen that the POD, FAR, and AWT obtained using UMASOD and ESPERTA were similar.

There is a scheme of SEP event predictors, called University of MAlaga Solar particle Event Predictor (UMASEP), with an approach that is very different to the approach presented here, because it correlates near-Earth particles with solar data [12,38,39,40,42,43,44,45]. A model of the aforementioned scheme is UMASEP-10 [42], whose model parameters were refined for obtaining better historical results. By using historical data of the period 1997–2014, the prediction of flare-associated SEP events by UMASEP-10 (version 2.0) yielded a POD of 93.3%, a FAR of 25.5%, and an AWT of ~4 h (see Table 5 for more details). Although these results were better in terms of POD and FAR than those of UMASOD and ESPERTA, the anticipation time (i.e., AWT) was much lower (worse). In general, the SEP event predictions of all the UMASEP models [38,39,40,42,43,44] require waiting for the arrival of the first particles at Earth, which is a strategy that yields better POD and FAR, but shorter AWTs (in the range of 8 min to 4 h) than the AWT provided by UMASOD and ESPERTA. For this reason, the radio-burst-based models can only be compared among themselves because they belong to a specific category of SEP event predictors, which process solar data only.

The results of the different models are summarized in Table 5.

5. Conclusions

In this study, a decision tree model was created from flare and radio data, obtained from the NOAA edited event list data and the NOAA/NASA SEP list to predict >10 MeV SEP events associated with flares. Our model UMASOD obtained a POD of 70.2% and a FAR of 40.2%.

We found that UMASOD led to outputs and results comparable to those derived by ESPERTA [10,11], which is the current state-of-the-art model in radio-burst-based SEP event predictors. The main advantage of our approach is that it analyzes solar data that are updated every 30 min and, thus, it may be operational; however, a disadvantage is that those SEP events associated with strong well-connected flares cannot be predicted. ESPERTA has not been operative because the radio data that this model processes are currently not available before the start of SEP events.

The obtained decision tree also showed that the main criteria to differentiate pre-SEP-event scenarios and non-pre-SEP scenarios are the peak and integrated flux for SXR flares, and radio type III bursts. The product of the integral of soft X-ray and type III radio bursts is also important as proposed by [10,11]. Type IIs were not included in the decision tree by the machine learning algorithm (J48). This study excluded type IVs, because the end of these sweep-frequency radio bursts is very likely to take place after the SEP event start time, and type Vs, because of the low probability of them taking place before the start of SEP events.