Black Holes and Complexity via Constructible Universe

Abstract

The relation of randomness and classical algorithmic computational complexity is a vast and deep subject by itself. However, already, 1-randomness sequences call for quantum mechanics in their realization. Thus, we propose to approach black hole’s quantum computational complexity by classical computational classes and randomness classes. The model of a general black hole is proposed based on formal tools from Zermelo–Fraenkel set theory like random forcing or minimal countable constructible model $L_{\alpha }$. The Bekenstein–Hawking proportionality rule is shown to hold up to a multiplicative constant. Higher degrees of randomness and algorithmic computational complexity are derived in the model. Directions for further studies are also formulated. The model is designed for exploring deep quantum regime of spacetime.

1. Introduction and Motivations

Susskind et al. (e.g., [1,2,3]) in a series of papers have approached the complexity of quantum systems. Their findings are particularly interesting in the case of black holes (BH) and the horizons which are formed in spacetime. This program can be seen as the effort toward understanding the regime where quantum mechanics (QM) and spacetime overlap each other as deeply involved physical structures. Thus far, we are left with separated formalisms of two fundamental physical theories i.e., QM and general relativity (GR) where this last certainly describes spacetime as dynamical entity. The celebrated Penrose–Hawking singularity theorems indicate that there has to exist a regime of spacetime where description by GR is not applicable any longer and where presumably certain theory of quantum gravity will have to find its place. This is where black holes are formed and where singularities transcending the usual GR description have to appear. Understanding BH leads in fact to understanding the quantum regime of spacetime and gravity (QG). However, we are facing here the crucial difficulty and we know neither the correct mathematical structure of QG nor even the more or less successful guess of it. Thus, the attitude to QG from the perspective of BHs should be based on the careful recognition of mathematics involved in this area keeping at the back of a head the possibility for a proper guess which would eventually emerge from the formalism. Historically, the Penrose–Hawking singularity theorems resulted with the careful studying of GR’s mathematical structure and finding its limitations. Now, we try to find proper indications coming from the quantum side (QM and BHs), rather than GR that could lead to understanding of QG. In particular, the classical world can be seen now as defining limitations for the QM formalism.

Besides the phenomenon of BHs, there exist even more aspects of QM that recently received much attention from researchers. One is what can be called quantum information processing and, in particular, the ‘mutual’ search for an effectively working version of a quantum computer. Anyway, ‘quantum computing’ in a general form is realized in nature in various ways as evolution of entangled or interfered states, which eventually undergo unpredictable wave function collapse, and the process can be used to characterize physical systems. This was an idea of Susskind et al. to work out intrinsic characteristics of BHs in terms of quantum computational complexity. In their analysis, quantum circuits appear where the minimal number of gates indicates the complexity of the quantum process (see below in this section). They argued that BHs are intrinsically realizing such quantum computational complexity and many physical properties of BHs like entropy are derivable from it. Another important aspect of QM recently under intense investigation is the problem of inherent randomness of QM. In mathematics, there exists a vast domain devoted to defining and studying various concepts of randomness and their interrelation with classical computational complexity (see, e.g., [4], Appendix B). Whether QM is actually random and what degree of randomness it realizes is a deep problem in general (see, e.g., [5,6]). We consider the domain of algorithmic complexity based on classical Turing machines as a classical one. From that point of view, the computational complexity referred to in the papers by Suskind et al. belongs to the quantum domain. The general premise we follow in this work is that the classical algorithmic computational complexity delineates limitations for the quantum one (similarly to the classical realm of spacetime setting limitations for quantum BH). However, the classical and quantum computational complexities overlap in a specific sense and this overlapping can be used to characterize quantum BHs and classical spacetime—and presumably gives insights about the mathematics of QG. In this paper, we address the question whether, and under what conditions, the quantum complexity of BHs can be seen as classically originated. Even confirmed to some degree, it would indicate that the QM realm of BHs and the classical realm of spacetime can be seen as overlapping domains from the complexity point of view (where the complexity links them both). Such approach is based on two important observations. Firstly, BHs are inherently characterized by their entropy (as the Beckenstein–Hawking area law) and the algorithmic complexity we use here is also related to entropy. Secondly, the binary sequences of ‘successes’ and ‘fails’ as resulted in the process of infinite fair coin tossing (with the precise probability $\frac{1}{2}/\frac{1}{2}$ at each toss) cannot be realized by a deterministic classical process [6]. It follows that randomness realized by such sequences has to be quantum even though the entire process seems to be describable classically. It seems to be, but actually it is not. In this way, randomness can be seen as another aspect of the overlapping domains of QM and spacetime realms. Finally, we carefully approach the mathematics suitable for the description of both realms. It seems that the most suitable mathematical formalism is one based on models of axiomatic set theory and this fact follows from the structure of QM lattice of projections $\mathbb{L}$. The basic reason behind such statement is ‘Solovay genericity’, the phenomenon known from random forcing in set theory and from algorithmic computational complexity and randomness where it is called ‘weak genericity’. Precisely, this kind of genericity is realized within a QM lattice of projections on infinite dimensional Hilbert spaces.

The entire project is embedded in formal mathematics, and various mathematical concepts appear that are not in direct everyday use by most of the physicists, which by itself may ‘hide’ the simplicity of basic ideas. There are notions like randomness, models of Zermelo–Fraenkel set theory, forcing or even axiomatic formal systems (that already require some familiarization with the usual mathematical practice). However, when one adopts a slight extension of accessible mathematical tools, the initially involving and logically distant ideas become rather direct and easily expressible. To facilitate access to the results in the paper, we have attached appendices where the reader can find indications and guidelines regarding basic constructions in QM and computational complexity. As already mentioned above, the important clues regarding mathematics of QG should come from the unifying description of BHs by formal set theory methods (e.g., [7,8]).

Now let us be more specific. Suskind et al. have proposed the measure of intrinsic computational complexity of states in a Hilbert space of dimension $2^K$, where K is the number of qubits. A way to the complexity went through the relational complexity $C(U,V)$ between two unaries, i.e., unitary complex matrices $U,V\in SU\left(2^K\right)$ where this last space is much bigger than the state space $CP(2^K-1)$—the complex projective space of dimension $2^K-1$. Let G be a set of quantum gates considered as fundamental.

$$C(U,V)=\mathrm{the}\mathrm{minimal}\mathrm{number}\mathrm{of}\mathrm{gates}{g}_i\in G\subset SU\left(2^K\right)\mathrm{such}\mathrm{that}U=g_1{g}_2\dots g_{k}V.$$

Then, the complexity of each $V\in SU\left(2^K\right)$ is defined as

$$C\left(V\right):=C(V,I),\mathrm{where}I\mathrm{is}\mathrm{the}\mathrm{identity}\mathrm{matrix}.$$

In fact, $C(U,V)$ is a right-invariant metric on $SU\left(2^K\right)$ which differs essentially from the usual inner product metric [1]

$$d(U,V)=arccos\mathrm{Tr}|U{V}^{†}|.$$

Then, the task is to find the structural ingredients of QM responsible for the complexity of quantum systems and BHs in particular. The quantum gates and circuits involved in the definitions of the complexity distance above are based on unitary evolution of states and, as such, do not refer to the collapse of a wave function taking place during a quantum measurement. In this case, we would live in a world of quantum computations that permits entanglement and maintains it without classical reduction. However, when we allow measurements on entangled systems, we still have much room for computational complexity in the resulting classical realm. In addition, the measurement in QM that enforces classicality is the source of randomness and unpredictability in QM [5,6]. This algorithmic complexity in classical contexts (based on classical Turing machines—see Appendix B) belongs to classical complexity theory. However, we expect that the degree of randomness it carries is high enough for giving an alternative to quantum computing point of view in the context of BHs. As we mentioned already, such expectation is supported by the result that classical 1-random behavior of the coin-tossing generating infinite binary sequence cannot be realized as a deterministic process and, in fact, it requires QM (e.g., [6]). Thus, ‘a kind of’ classical randomness in principle can be used to mimic quantum phenomena.

Our approach is based on the method of formalization, as developed in e.g., [8,9]. It relies on using models of axiomatic set theory (Zermelo Fraenkel set theory possibly with the axiom of choice—ZFC) to quantum mechanics and gravity especially for the overlapping domain of QM and ‘classical’ spacetime. The reason for using varying models of ZFC is the inherent structure of the lattice $\mathbb{L}$ of QM where the set-theoretical random forcing is generated by atomless Boolean algebras of projections (the measure algebras). We present the construction, along with building the BH model, in Section 3. It is shown there that local Boolean contexts in $\mathbb{L}$ are atomless Boolean algebras and that it leads to the non-trivial forcing (see also Appendix A). This random forcing governs the change of the model according to $L_{\alpha }\to L_{\alpha }\left[r\right]$, where r is certain random infinite binary sequence. Next, we follow the observation that the variety of models can play the role of additional internal degrees of freedom (DoF) in physical theories [8]. Applying these forcings and such generated DoF to the BH model built in Section 3, the rule of proportionality of entropy to the surface of the horizon of a BH has been derived in Section 3.1. The second main result of this paper also relies on forcing and ZFC models. Namely, the randomness of infinite binary sequences—r’s (of possible outcomes of QM measurements added by forcing extensions to $L_{\alpha }$) leads to the characterization of the inherent randomness assigned to BHs. This is our Theorem 1 which states that given any class $0^{\left(n\right)},n=0,1,2\dots$ known from the algorithmic computability theory (see Appendix B), one finds that the relative to $0^{\left(n\right)}$ 1-randomness (i.e., in fact n-randomness) is realized by generic BHs. Thus, again, the source of the results above lies in the structure of the QM lattice $\mathbb{L}$ that governs the change of the ZFC models by random forcing. We expect that this very fact should survive, in this or another form, in a final version of QG. Such statement is a hypothesis; however, uncovering formalism substantiating, it can be considered as the third main result of the paper.

The work is organized as follows: in the next section, we will briefly review the ZFC models techniques and explain (following [10,11]) that mathematics of QM can be formulated in the minimal standard countable transitive model (CTM) of ZFC, $L_{\alpha }$. However, the statistical outcomes of QM are not $L_{\alpha }$-expressible. In the subsequent section, we will discuss the randomness and computational complexity from the perspective of $L_{\alpha }$ and QM in it. Having developed the general setup for complexity in QM (based on random forcing and models of ZFC), we will apply it to derive BH horizon area law in Section 3.1 and to characterize the computational complexity of BH in Section 3.2 (Theorem 1). These results are based on the lattice $\mathbb{L}$ that supports the random forcing, and this fact is presented in Section 3 and Appendix A. More thorough and complete treatment of the relation of QM and randomness will be the topic of a separate publication.

2. Mathematical Formalism of QM in the Minimal Constructive Model of ZFC

While using mathematics in physics, its formal foundations are mostly of no concern and are usually understood intuitively. Actually, even most mathematicians in their research do not need to use directly methods of model theory. This situation makes the fact that QM formalism has deep connections with axiomatic set theory even more interesting.

Set is a basic concept of most of mathematics—even objects in physical theories like QM are formally sets, e.g., operators or Hilbert spaces. Set theory is the basis for analysis, algebra, topology, etc.—simply for mathematics as it is used in theoretical reasoning by physicists. It should be described axiomatically via methods of formal logic to avoid technical problems like Russell’s paradox. The most common is Zermelo–Fraenkel set theory with the axiom of choice, abbreviated as ZFC, and it is recognized as foundation of (almost all of) mathematics. A model of ZFC is a mathematical structure $M=(\mathcal{M},\diamond )$ (an interpretation) that satisfies all axioms and derived in ZFC formulas. Model M is said to be standard when ⋄ is the usual membership relation ∈ and M is called transitive if $\mathcal{M}$ is a transitive class (each of its elements is also its subclass). Referring to standard transitive models is typical and one should treat such references as technical in the next sections. The important thing to realize here is that each theorem of ZFC must be true in all its models. Hence, the usual mathematical relationships stated as theorems should not cause any problems when expressing formalism and postulates of QM within a model of ZFC.

There exist many non-isomorphic models of ZFC. An important concept of ‘absoluteness’ helps us to grasp some of the differences between them (it is related to ‘seeing’ formal objects as from inside or outside of a model). For example, a property $\psi \left(x\right)=‘\mathrm{x}\mathrm{is}\mathrm{a}\mathrm{real}\mathrm{number}’$ is absolute. This means that any set satisfying $\psi$ does it whether we relate it to some standard transitive model or not. On the other hand, $\chi \left(x\right)=‘\mathrm{x}\mathrm{is}\mathrm{the}\mathrm{set}\mathrm{of}\mathrm{real}\mathrm{numbers}’$ is not absolute. When we consider a collection of all sets satisfying $\psi$, then we will obtain the class $\mathbb{R}$ of all reals. We know that there exist (and are relevant for this paper) standard CTMs of ZFC. Let $M=(\mathcal{M},\in )$ be such a model. We can denote the set from this model that satisfies $\chi$ as $R_M$. Since, from the outside, $\mathcal{M}$ is countable, then $R_M$ is countable too and hence it cannot be equivalent to $\mathbb{R}$ (in fact, the relation between the two—from the outside M perspective—can be stated as $R_M=\mathbb{R}\cap \mathcal{M}$). However, inside model M, we do not know about any ‘missing’ reals and $R_M$ is actually uncountable from the inside M point of view (so-called Skolem’s paradox). Moreover, we have formal tools to extend a model of ZFC, among other things possibly adding some of the ‘missing’ reals (in non-trivial cases). The method for extending a ZFC model is called ‘forcing’ and there are various versions of it (differentiated also by what ‘kind’ of real numbers are added). When a standard CTM M is extended via appropriate forcing to some $M\left[G\right]$ (extension by addition of so-called generic ultrafilter G), then their sets of reals are related in a similar manner, namely $R_M\subset R_M\left[G\right]$ (when seen from the outside of M/inside of $M\left[G\right]$). Since the real numbers can be seen as infinite binary sequences—and these can be related to repetitions of a given quantum measurement—this fact is of special interest for us.

Gödels’s constructible universe (a particular model of ZFC) is a class of sets that can be fully described by simpler sets—starting with an empty set, we construct more and more complicated sets by applying basic set operations to the sets from previous stage. The construction is ordered by ordinal numbers—transitive sets whose all elements also are transitive sets (the finite ones are exactly natural numbers). Namely, for each $\beta \in Ord$ (class of all ordinals), we obtain the stage in so-called constructible hierarchy

$$L_{\beta }=\bigcap _{\delta <\beta }P\left(L_{\delta }\right)\cap I(L_{\delta }\cup \left\{L_{\delta }\right\}),$$

where $P\left(A\right)$ is a power set of A and $I\left(A\right)$ is the smallest set containing A and closed under the following operations: creating ordered and unordered pairs, set difference, Cartesian product, performing permutation of an ordered triple, and taking the domain of a binary relation. The constructible universe is defined as the union of all $L_{\beta }$, and it is a standard transitive model of ZFC. However, to obtain a minimal constructible mathematical universe to work in, we do not need to sum up all the stages. In particular, the countable set defined as $L_{\alpha }={\bigcap }_{\delta <\alpha }{L}_{\delta }$, where $\alpha$ is the smallest ordinal for which there exists a standard CTM of ZFC that does not contain it, is the standard minimal CTM of ZFC.

For a comprehensive exposition along with the discussion on formal intricacies of all the topics mentioned above, we refer an interested reader to classical manuscripts, like [12].

Now, we can address the issue of expressing the mathematics of QM in $L_{\alpha }$. According to the discussion above, mathematical theorems of functional analysis, etc. that are used in QM calculations are true in any ZFC model and hence will not cause problems here. What is important—and needs additional commentary—if we want $L_{\alpha }$ to be the carrier for mathematics of QM is the representation of postulates of QM. What interferes with relating QM to the model are non-absolute defining properties of basic structures, e.g., if H is a Hilbert space inside $L_{\alpha }$, it may not be the Hilbert space when seen from outside of it (or in another standard transitive model that contains $L_{\alpha }$ as a submodel). We should indicate here that, for further considerations, it is only needed that one can express in $L_{\alpha }$ the appropriate mathematical objects from the postulates and that, after extending the model via forcing, one can appropriately relate them to their counterparts in the new model. The existence of sequences representing outcomes of (possibly infinite) repetitions of a given measurement (when seen from the outside of the model) is a separate problem (see the discussion on reals in models above) and by itself was discussed more extensively elsewhere (e.g., in [13]). To address absoluteness issues, one can proceed as follows. Following Benioff’s technical assumptions, we will consider only observables that are questions (yes/no outcome of a measurement), but one can carry on analogically without this restriction. Inside the model $L_{\alpha }$, each quantum system is studied over a complex Hilbert space $H_{L_{\alpha }}$ and states are represented by density operators from the set $B\left(H_{L_{\alpha }}\right)$ of bounded linear operators over $H_{L_{\alpha }}$. We want these points to be true:

(a)

Outside the model $L_{\alpha }$, there exists a Hilbert space H and an isometric monomorphism U from $H_{L_{\alpha }}$ into H.

(b)

Outside the model $L_{\alpha }$, there exists an isometric monomorphism V from $B\left(H_{L_{\alpha }}\right)$ into $B\left(H\right)$.

(c)

Let S and Q be collections of state preparation procedures and question measuring procedures, respectively. There exist maps $f:S\to B\left(H\right)$ and $g:Q\to B\left(H\right)$ such that, for any $s\in S$ and $q\in Q$, the values $f\left(s\right)$ and $g\left(q\right)$ are respectively the density and projection operators (outside $L_{\alpha }$). There also exist analogical maps $f_{L_{\alpha }}$ and $g_{L_{\alpha }}$ such that appropriate values are density and projection operators from $B\left(H_{L_{\alpha }}\right)$ (inside the model $L_{\alpha }$). Moreover, in the respective domains of $f_{L_{\alpha }}$ and $g_{L_{\alpha }}$, the mean values of these projections in the set of equally prepared states by these density operators are equal outside $L_{\alpha }$, i.e.,

$${\mathrm{Tr}}_{L_{\alpha }}\left(f_{L_{\alpha }}\left(s\right)g_{L_{\alpha }}\left(q\right)\right)=\mathrm{Tr}\left(f\left(s\right)g\left(q\right)\right).$$

Formal constructions showing how one could always find appropriate maps and spaces from these points can be found in Benioff’s original work (parts B, C, and D of Sec. III, [10]). All considerations were expressed generally as interplay between the perspective of $L_{\alpha }$ and outside of this model, but one can proceed analogically in the case of any standard transitive model M of ZFC that extends the minimal one, $L_{\alpha }\subset M$. Note also that the remarks of this section regarding QM in $L_{\alpha }$ might be applied basically to any standard transitive model of ZFC.

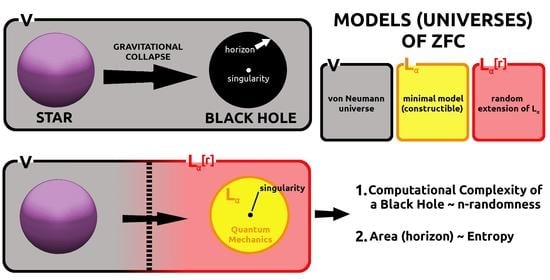
3. Models of ZFC and Computational Complexity of BH’s State Space

In this section, we consider the situation where, during the formation of a BH in spacetime, as a result of the gravitational collapse of a star, the state where QM is in $L_{\alpha }$ (as in the previous section) is attainable—and then we draw conclusions from such scenario. To realize this, we need to construct a mathematical model of BH based on the varying models of ZFC. While performing this task, we present step by step formal ingredients of a general mathematical setup. Thus, in points 1–5 below, together with Appendix A, elements of QM and operator algebras appear which intertwine with constructions from formal ZFC. Finally, point 5 explains how random forcing arises in QM from $\mathbb{L}$ which leads to a change of the ZFC model. This last observation opens the way toward algorithmic computational complexity in the context of BHs via random forcing extensions (see Theorem 1).

Let us consider the increasing density of energy in spacetime due to the gravitational collapse of a sufficiently massive body and corresponding increase of the curvature of spacetime as basic starting points. In principle, the corresponding expressions are unlimited and hence divergent. Consider a 4-submanifold of spacetime $N\subset M^4$ with increasing 4-curvature and let it be a part (say open submanifold) of 4-sphere $S^4$ with decreasing radius r, i.e., $k\sim 1/r^2$ and $N\subset S^4\cap M^4$, where k is the Ricci scalar curvature. General relativity (GR) tells us that any such region in spacetime can be covered by local, diffeomorphic to the flat ${\mathbb{R}}^4$, patches (with the Minkowski metric). When $r\to 0$, the diameters of the patches are also decreasing to zero showing the singularity of GR in such limit. Let us instead assume the scale of density of energy ${\rho }_s$ and the radius $r_s$ such that, for each density $\rho >{\rho }_s$ and radius $r<r_s$, the local patches of the manifold have finite and positive diameters. However, they are not any longer the local patches of a spacetime submanifold. In this way, we have dismounted a highly curved 4-submanifold into the set of local patches of finite diameters not exceeding $\delta >0$ and the submanifold N with the 4-curvature bounded from below (bigger than $1/r_s^2$). Then, the set of patches ${\left\{U_i\right\}}_{i\in I},U_i\stackrel{\mathrm{diff}.}{\simeq }{\mathbb{R}}^4$ will take part in the quantum description while the submanifold N, with its smooth atlas of arbitrary small size local patches, will be associated with the still singular classical GR description.

To understand this via set theory, the crucial element is that, during the collapse, the model of ZFC we work in can be weakened or changed into another model of ZFC so that the model changes when BH is forming. More precisely, behind the horizon quantum description requires the CTM $L_{\alpha }$ which differs from the model M before the horizon. We can think of M as a model of ZFC with a ‘more complete’ real line $R_M$ compared to $R_{L_{\alpha }}\subset R_M$. One might consider $R_M$ as $\mathbb{R}$ and hence $R_{L_{\alpha }}$ is its countable dense subset. There are few comments regarding this point. First, neither M nor $L_{\alpha }$ can prove that they are models of ZFC nor that there exists a ZFC model at all. If any of them could, this would prove the consistency of ZFC, which is known to be unprovable in this way (Gödel’s incompleteness results). In fact, we do not so far have any proof or disproof of the consistency of ZFC. Moreover, when $L_{\alpha }$ is not a submodel of M (and certainly M is not a submodel of $L_{\alpha }$), then M does not ‘see’ some sets of $L_{\alpha }$. This means that any observer using tools available in M has no (or at best limited) access to sets in $L_{\alpha }$. This situation represents set-theoretic counterpart of the horizon in physics of BHs which we make use of. Furthermore, given the two models as above on both sides of the horizon from the point of view of spacetime in which BH was formed, the model $L_{\alpha }$ resides in a, bounded by horizon of the BH, singular region of spacetime, i.e., it is constructed in the bounded by two-dimensional horizon three-dimensional space (+internal time) such that the singularity is described by QM in $L_{\alpha }$. QM singularity and spacetime horizon are linked by random forcings generated by the lattice of projections on the infinite dimensional separable complex Hilbert space states (see [8]). More precisely, the set ${\left\{U_i\right\}}_{i\in I}$ of local open frames (with finite diameters) spans both, the local structure of the horizon and the quantum state space of BH, and the set emerges from QM expressed in $L_{\alpha }$. This set replaces GR-singular open cover of the infinitely small (part of) spacetime manifold crushed to a singular region and develops horizon.

In the remaining part of this section, we will collect basic mathematical facts in favor of the above scenario and then draw general conclusions regarding BHs and complexity.

1. Let $\mathcal{H}$ be a separable complex Hilbert space and $dim\mathcal{H}=\infty$. Let $\mathbb{L}\left(\mathcal{H}\right)=\mathbb{L}(\wedge ,\vee ,0,1)$ be the lattice spanned by projections p on closed linear subspaces $A,B\subset \mathcal{H}$, $p^2=p$, or equivalently the lattice of closed linear subspaces of $\mathcal{H}$. Here, $A\vee B:=\overline{A+B}$ (the minimal closed linear subspace containing A and B); $A\wedge B:=A\cap B$; $\neg A:=\left\{\mathrm{the}\mathrm{orthogonal}\mathrm{completion}\mathrm{of}A\mathrm{in}\mathcal{H}\right\}$; $0:=\varnothing$; $1:=\mathcal{H}$. In general, ($dim\mathcal{H}\ge 2$), the lattice $\mathbb{L}\left(\mathcal{H}\right)$ is nondistributive respecting the fact that projections might not commute.

2. The local Boolean context in $\mathbb{L}:=\mathbb{L}\left(\mathcal{H}\right)$ is a maximal complete Boolean algebra of projections chosen from the lattice $\mathbb{L}$ (so-called MASA—maximal Abelian subalgebra). There is strict 1:1 correspondence between classical contexts defined on the algebra of linear operators as a maximal subalgebras of commuting self-adjoint operators (s.a.) chosen from $\mathcal{L}\left(\mathcal{H}\right)$ (this last part extends the space of bounded linear operators $B\left(\mathcal{H}\right)$ on $\mathcal{H}$ ([14], Remark 9.4.2, p. 670) and MASAs built of the projections from $\mathbb{L}$ (see Appendix A). Thus, given the classical (Boolean) context spanned by maximal set of commuting observables, we have equivalent Boolean context given by the complete maximal Boolean algebra of projections. The given s.a. $a\in \mathcal{L}\left(\mathcal{H}\right)$ belongs to certain commutative von Neumann algebra (containing maximal set of commuting observables along with a). On the other side, a belongs to certain complete maximal Boolean algebra B of projections (containing all projections appearing in the spectral measure of a) and both ways are equivalent in a sense of Lemma (A1) and Equation (A2) from Appendix A.

3. The importance of $B\subset \mathbb{L}$ comes from the fact that a way from deep quantum regime to the classical 2-valued window goes through such Boolean local context B. In particular, any reduction which is assigned to a measurement in QM also factors through such B: any projection to an eigenspace, containing an eigenstate of an observable a, belongs to certain MASA B from $\mathbb{L}$, which is picked with probability given by Born’s probability rule.

4. Recall that $dim\mathcal{H}=\infty$. Maximal abelian von Neumann subalgebras of $\mathcal{L}\left(\mathcal{H}\right)$ in this case all have the following presentation (are unitarily equivalent to) ([14], Th. 9.4.1)

$$\begin{array}{c}{N}_a\oplus N_c\mathrm{where}{N}_a\mathrm{is}\mathrm{the}\mathrm{atomic}\mathrm{part}\mathrm{and}{N}_c\mathrm{the}\mathrm{continuous}\mathrm{part};\\ N_a\mathrm{is}\mathrm{generated}\mathrm{by}\mathrm{the}\mathrm{projections}\mathrm{on}\mathrm{the}\mathrm{vectors}\mathrm{of}\mathrm{the}\mathrm{base}\mathrm{in}\mathcal{H};\\ N_c\mathrm{is}\mathrm{the}\mathrm{algebra}\mathrm{of}(\mathrm{essentially}\mathrm{bounded})\mathrm{measurable}\mathrm{functions}{L}^{\infty }([0,1],\mu )\end{array}$$

(1)

where $\mu$ is the Lebesgue measure on the $\sigma$-algebra of Borel subsets on $[0,1]$.

It follows that MASAs in $\mathbb{L}$ for $dim\mathcal{H}=\infty$ have the general form

$$B=B_a\oplus B_c,B_a\mathrm{is}\mathrm{the}\mathrm{atomic}\mathrm{Boolean}\mathrm{algebra},B_c\mathrm{is}\mathrm{the}\mathrm{measure}\mathrm{algebra}B.$$

(2)

B is defined as the algebra of Borel subsets of $[0,1]$ modulo the ideal $\mathcal{N}$ of $\mu$-measure zero Borel subsets

$$B=Bor\left([0,1]\right){/}_{\mathcal{N}}.$$

(3)

Lemma 1

([14,15]). B is atomless Boolean algebra.

The above property really distinguishes an infinite dimensional case, since

Corollary 1

([14,15]). If $dim\mathcal{H}<\infty$, then maximal complete Boolean algebras of projections chosen from the lattice $\mathbb{L}$ are atomic.

A well-known fact that quantum observables like position or momentum require infinite dimensional Hilbert space of states shows that the atomless Boolean algebras involved always emerge here where spacetime overlaps with QM in a non-trivial way. This is the case of the description of BHs presented in this paper.

5. As we have already noticed, B—being a Boolean context for the QM lattice $\mathbb{L}$—is the unavoidable step toward reaching 2-valued stage of classical world. This can be implemented as a homomorphism $h:B\to 2$ where 2 is the 2-valued classical Boolean algebra $\{0,1,\wedge ,\vee \}$, but we require that the completeness of B is somehow maintained by such h. More precisely, $h:B\to 2$ should be completely additive in a sense that for any subfamily $S\subset B$ of B in $\mathbb{L}$ the following holds

$$h(\bigvee S)=\bigvee \left\{h\right(s\left)\right|s\in S\}.$$

(4)

6. Now, let us work with B supposing that QM is in $L_{\alpha }$ as in Section 2. It follows that Bs are also internal algebras, i.e., measure algebras $Bor\left([0,1]\right){/}_{\mathcal{N}}$ in $L_{\alpha }$ and, as such, they are still atomless Boolean algebras in the model. Then, the homomorphism $h:B\to 2$ carries very important information when considered internally to $L_{\alpha }$. First, one cannot fulfill the condition (4) in $L_{\alpha }$. The reason is the fact that, when $S\subset B$ and B as above is in $L_{\alpha }$, then $h^{-1}\left(1\right),1\in 2=\{0,1\}$ is so-called generic ultrafilter in B (in $L_{\alpha }$), e.g., [8]

$$h^{-1}\left(1\right):={\{b\in B|h\left(b\right)=1\}}_{L_{\alpha }}=\mathcal{U}(\mathrm{a}\mathrm{generic}\mathrm{ultrafilter}\mathrm{in}B).$$

However, it is known that, whenever B is atomless in $L_{\alpha }$, the generic ultrafilter $\mathcal{U}\notin L_{\alpha }$ [12]. This means that, for any measurement, if QM is in $L_{\alpha }$, then h (giving rise to classical results) does not exist in $L_{\alpha }$. A natural question that follows would be if there exists any model $M^{\prime }$ of ZFC containing $L_{\alpha }\subset M^{\prime }$ such that $h\in M^{\prime }$? The answer is positive and there indeed exists such a minimal extension of $L_{\alpha }$, denoted $L_{\alpha }\left[h\right]$, and it contains the homomorphism h. The model $L_{\alpha }\left[h\right]$ is known in set theory as the random forcing extension of $L_{\alpha }$ [12] and, in the context of this paper, it describes the measurement, along with its classical outcome, consistently. Thus, we have reached the scenario where QM world is explored by classical windows and the process factors through the set-theoretic forcing extensions of a certain model of ZFC.

Now, we are ready to draw further conclusions regarding BHs.

3.1. BH Horizon

The following picture emerges: given the model $L_{\alpha }$ describing the region containing the singularity of BH, one is directed toward the horizon via forcings extensions $L_{\alpha }\left[h\right]$ as in the previous subsection. The family of such extensions can not be reduced to a single extension and the variety of them corresponds to the family of local coordinate frames defined on the horizon [8]. The important point of this approach is the effective reduction of the Hilbert space dimension from infinite to a certain finite value to be determined shortly. The reduction takes place due to the presence of the horizon which effectively bounds the dimensionality and also explains the statistical QM origins of entropy. The BH entropy originates in QM regime and is not determined by the entropy of matter and energy creating a BH in the collapse. It is rather the structural formal property of the presented model.

Forcing extensions starting in $L_{\alpha }$ and ending at the horizon with $\{L_{\alpha }\left[h_i\right],i\in I\}$, correspond to the projections of 4-dimensional local coordinate frames onto two-dimensional ones on the horizon. Projecting on the horizon means leaving with the formal description by the i-th local extension $L_{\alpha }\left[h_i\right]$ but also relate the purely QM regime with the classical geometry of the horizon. What is the role of the number of forcing extensions? It certainly relates to the number of local two-dimensional ‘patches’ of the horizon. Let the area of the horizon be ${\mathcal{A}}_h$. Each (geometrical) point $x\in \mathrm{Hor}$ of the horizon belongs to certain open two-dimensional domain $U_x^{\left(2\right)}$ in $L_{\alpha }\left[h_x\right]$ and this last one is the projection of a 4-dimensional domain $U_x$—if the diameters $\left\{{\delta }_x\right|x\in \mathrm{Hor}\}$ of each $U_x^{\left(2\right)}$ are such that the minimal length l bounds them from below, i.e., ${\exists }_{l>0}{\forall }_{x\in \mathrm{Hor}}{\delta }_x>l$ (this agrees with the discussion at the beginning of Section 3). Thus, the minimal number N of local domains generated by QM in $L_{\alpha }$ is finite

$$\mathrm{the}\mathrm{number}\mathrm{of}\mathrm{forcing}\mathrm{extensions}{L}_{\alpha }\left[h_i\right],i\in J_{\min .}=\left|J_{\min .}\right|=N<\infty$$

(5)

where $J_{\min .}$ is finite since the area ${\mathcal{A}}_h$ is finite. Thus, we have minimally N classical patches covering the horizon that come from a kind of classical reduction of quantum superposed states—on the QM side of $L_{\alpha }$, there are superposed states that undergo reduction to classical patches. The minimal such superpositions are given by bipartite states which makes this similar to the case of N qubits. Then, we ask about the entire dimensionality of a Hilbert space allowing for such generalized quantum computing processes that would be the minimal dimension of the Hilbert space in our model of BH. Thus, supposing that each horizon’s patch emerges from the reduction of a superposed bipartite state, we can estimate the minimal dimensionality of the Hilbert space of states ${\mathcal{H}}_{\mathrm{BH}}$ of BH (e.g., [16]) as

$$dim{\mathcal{H}}_{\mathrm{BH}}=2^N.$$

(6)

Hence, the minimal state space of BH is spanned on $2^N$ independent states. We can also approximate the entropy of BH in this approach. The entropy reads $S_{\mathrm{BH}}\sim {log}_2{2}^N=N$ and thus taking the proportionality coefficient A it is $S_{\mathrm{BH}}=A·N$. In terms of the BH horizon area ${\mathcal{A}}_h$, we obtain

$$S_{\mathrm{BH}}=A·N=A·\frac{{\mathcal{A}}_h}{l^2}$$

(7)

which is the usual Bekenstein–Hawking formula up to the coefficient A. Within these general considerations, we do not determine it.

One could wonder how it is possible to have 4-dimensional regions bounded by a two-dimensional horizon. The answer is related to the expressible power of models of ZFC and is also responsible for BH complexity as we will see in the next subsection. In any ZFC model, one can define not only any space, like ${\mathbb{R}}^n,n\in \mathbb{N}$, but also any manifold or even any set of arbitrarily high cardinality, not only $\omega ,{\omega }_1$, but even higher. Given the model confined in the behind horizon domain, we have formally all objects definable in it. This special feature is the consequence of that that a model of ZFC changes when crossing the horizon. Thus, the model confined to the behind horizon region is different than the outside model. QM and GR are expressible in the models. More generally, everything that can be proved formally in ZFC remains provable literally in the same way in every model. There are, however, specific sentences independent on the axioms which still can be proved in one forcing extension and its negation in another, and they can make difference between the extended models. This phenomenon is related to randomness in QM—we do not investigate this topic here any further (for more details see [17]), but we do apply it when analyzing computational complexity below. On the set-theoretical side, this is connected with relative consistency and provability by forcings in the extended models. It is fair to say that there is a great variety of forcing procedures known for mathematicians but precisely one—the so-called Solovay forcing, which is responsible for randomness, is realized in QM [8,18].

3.2. Computational Complexity and BHs

Thus, behind the horizon, the model $L_{\alpha }$ is changing toward the family $L_{\alpha }\left[h_i\right],i\in I$, and this generates the local descriptions of the horizon. This process can also be responsible for the computational complexity in the context of BHs. Randomness and computational algorithmic complexity are in general very wide domains of intense mathematical enquiries, e.g., [4,19,20], and, to manage it on the reasonable number of pages, we develop here the main line of argumentation while leaving more formal definitions and properties to Appendix B. However, for more complete and systematic picture, we refer readers to excellent monographs as above.

The phenomena of random behaviour, randomness, and related computational complexity can be expressed mathematically by properties of infinite binary sequences. Due to use of ZFC models, this presentation is directly applicable to our model of BHs. To better understand this, let us take closer look at certain aspects of randomness of finite and infinite sequences and their relation to the computational complexity. The sequences can model the outcomes of the series of QM measurements, but this is not mandatory, which means that, even in the formalism of QM, there is a room for such random behavior without interpreting the infinite sequences as outcomes. The essential examples are given by the completely additive homomorphisms $h_i$ which are modeled by a random infinite sequences, i.e., those which are added by forcings as in $L_{\alpha }\left[h_i\right]$ (see [5]). These infinite sequences are represented formally by random real numbers which are random binary $\{0,1\}$ sequences (e.g., ([12], p. 243), [18]). The sequences are random with respect to $L_{\alpha }$ since they fulfill the following defining property [RAND] of randomness [18]

[RAND] A binary infinite sequence $r\in R_{M\left[r\right]}$ is random with respect to the model M if r omits all Borel sets of measure zero coded in M.

Now we see that, due to expressing QM in $L_{\alpha }$ and taking it as M above, we are able to confine randomness of infinite sequences within the behind horizon region of BH. Next, we are going to express the computational complexity intrinsically characterizing BHs by relating it to randomness as above. The interplay between randomness and computational complexity is a vast subject by itself (see, e.g., [4,19]) and here we only touch a few aspects relevant in the BH context. First, let us approach randomness of infinite binary sequences (reals) from the Cantor space $2^{\omega }$ via Turing computability (as we noted above, these reals correspond to $h_i$’s in our description of BHs). In Appendix B, some useful facts are presented about Turing classes and arithmetical classes of sets needed here.

Randomness of infinite sets and binary sequences can be defined in various ways. However, four main attitudes exist: patternless structures (the measure-theoretic paradigm), incompressibility property (the computational paradigm), unpredictability and genericity—that appear to be equivalent to the so-called 1-random case (except genericity). Even though they diverge in higher random classes, there are still plenty of cross properties—that have been developed within the years—that characterize one of them by the others [4,6,19]. Genericity refers to the relation of forcing notions to randomness, and we have distinguished it as a valid approach to randomness. In fact, generic sets are frequently and deeply present in all other three classes above but also develops a specific field in which complexity of BHs is naturally expressible. Our generic class of random phenomena contains in particular Solovay (random) forcing but also Cohen forcing (and some others). Cohen forcing usually is understood when world genericity appears in random phenomena [4]. The great exposition of genericity in this wider context (containing also Solovay forcing) can be found in [21].

The [RAND] property above is the example of patternlessness within the genericity class (Solovay forcing). The definition by Martin-Löf (see Appendix B), Solovay, or Schnorr are instances of patternlessness and are based on the omitting of the measure zero sets from suitable computability class. Depending on the computational strength of the class of sets of measure zero, one obtains corresponding strength of randomness. It is complemented by the requirement that random sequences belong to all full measure 1 unspecific sets.

The computational complexity of strings refers to incompressibility that we will discuss briefly below. There exist functions that measure complexity of binary sequences—aiming at expressing their randomness. One of the historically first such objects are plain Kolmogorov complexity C and Kolmogorov complexity K. Let $\sigma \in 2^{<\omega }$, i.e., $\sigma$ is a finite binary string, and let $f:2^{<\omega }\to 2^{<\omega }$ be a partial computable function. Then, the Kolmogorov complexity of $\sigma$ with respect to f reads

$$C_f\left(\sigma \right):=min\left\{\right|\nu \left|\right|f\left(\nu \right)=\sigma ,\nu \in 2^{<\omega }\}\mathrm{where}\left|\nu \right|\mathrm{is}\mathrm{the}\mathrm{length}\mathrm{of}\nu .$$

Then, the finite sequence $\sigma$ is random relative to f when $C_f\left(\sigma \right)\ge \sigma$ (one cannot perform any algorithm of ‘length’ related to f shorter than $\sigma$ to describe or compute $\sigma$). The dependence on f is unnecessary since there exists the universal partial computable function U such that, for each f as above, there exists a finite binary sequence ${\nu }_f$ that

$$f\left(\sigma \right)=U\left({\nu }_f\sigma \right)\mathrm{for}\mathrm{all}\mathrm{partial}\mathrm{computable}f:2^{<\omega }\to 2^{<\omega }.$$

Then, $C_U\left(\sigma \right)$ is the plain Kolmogorov complexity of $\sigma$ (e.g., [4]).

To deal with infinite sequences and study their algorithmic randomness, one defines so-called prefix-free Turing machines. A prefix-free subset $A\subset 2^{<\omega }$ contains such $\sigma \in 2^{<\omega }$ that any proper extension $\tau$ of $\sigma$ does not belong to A. A prefix-free function $f:2^{<\omega }\to 2^{<\omega }$ is such function with prefix-free domain. A prefix free Turing machine is T with domain (a set of sequences on which T operates) being a prefix-free subset of $2^{<\omega }$. A function $U:2^{<\omega }\to 2^{<\omega }$ is a universal partial computable prefix-free function if, for each partial computable prefix-free function $f:2^{<\omega }\to 2^{<\omega }$, there exists a string ${\nu }_f$ such that

$$f\left(\sigma \right)=U\left(\sigma {\nu }_f\right)\mathrm{for}\mathrm{all}\sigma \in 2^{<\omega }.$$

Then, fixing U, we can define the Kolmogorov’s prefix-free complexity of $\sigma$, $K\left(\sigma \right)$ as

$$K\left(\sigma \right):=C_U\left(\sigma \right).$$

The definition of n-random sequences $\sigma$, given in Appendix B, refers directly to the arithmetical complexity classes ${\sum }_n^0$ (see Appendix B) which means that randomness is deeply involved in computational complexity (and conversely). Below, one finds some examples of how it can go.

(a) The set A is n-random ⇔A is 1-random relative to $0^{(n-1)}$ (A is 1-random computably enumerable (c.e.) set from $0^{(n-1)}$) ([4], Cor. 6.8.5, p. 256).

(b) The set A is n-random ⇔$K^{0^{(n-1)}}(A\upharpoonright n)\ge n-O\left(1\right)$ ([4], Cor. 6.8.6, p. 257). Here, $A\upharpoonright n$ is taking n elements of c.e. set A and $K^{0^{(n-1)}}$ is the relativization of the Kolmogorov prefix-free complexity K to $0^{(n-1)}$.

(c) A set A is ∞-often C-random if there are infinitely many n such that $C(A\upharpoonright n)\ge n-O\left(1\right)$. Then, it holds that

$$A\mathrm{is}2-\mathrm{random}\iff A\mathrm{is}\infty -\mathrm{often}C-\mathrm{random}.$$

(d) A is 1-random ⇔${\sum }_{n\in \mathbb{N}}{2}^{n-K(A\upharpoonright n)}<\infty$ (and there are many other results of this kind about randomness and computational complexity).

Our concern now is to find a degree of algorithmic computational complexity assigned to BHs as formed in spacetime. We already noticed that random forcing (Solovay) is apparently present as the building block of the presented model of BHs (see [RAND] above). This is why we are going to analyze the complexity in the model via generic randomness (e.g., [21]). The crucial observation is the following result:

Theorem 1.

The computational complexity realized in the forcing model of BH based on $L_{\alpha }$ is at least that of 1-random sequence relative to $0^{\left(n\right)}$ for all $n\in \mathbb{N}$.

The proof of this theorem relies on the following two theorems:

Theorem 2.

([21], Th. II.4.6, p. 25) Weak n-randomness (relative to C) ⇔ Solovay n-generic randomness (relative to C), for arbitrary $C\in 2^{\omega }$.

Theorem 3.

([21], Th. II.5.1, p. 26) C-weak $(n+1)$-randomness ⟹C-n-randomness ⟹C-weak n-randomness, $n\ge 1$.

It remains to note that the [RAND] property means Solovay $\omega$-genericity (relative to $L_{\alpha }$) holding for all $n\in \mathbb{N}$ and taking place for BHs in our model. From Theorem 2, weak n-randomness holds for all $n\ge 1$ and, from Theorem 3, one infers that n-randomness for all $n\ge 1$ is attained in the presented model of BH. However, from the property (a) above, the statement of the theorem holds true.

Note that the arithmetical hierarchy (see Appendix B), on which the above results are based, comprises sets which are definable without parameters in the fragment of ZFC namely in hereditary finite model of sets, $(HF,\in )$, where the axiom of infinity does not hold ([12], p. 480). $L_{\alpha }$ is a model of all axioms of ZFC, and this shows that the results are independent in this respect on the model $L_{\alpha }$. The thorough discussion of this point will be performed in the separate publication.

4. Discussion

We presented a model of BH complexity based on classical notions of computational complexity. However, we allowed dynamical pattern of models of ZFC such that the working universe of sets undergoes sudden change while crossing the horizon to another model of ZFC. In this respect, this is the continuation of our previous recent works [8,9]. Physically, the change of a model depends on the scale of density of energy and we do not specify precisely the values but expect they should be found in the Planckian scales. Instead, we tested the entire possibility of the model-changing in the context of BHs. Formally, working in certain model of ZFC is advantageous since we can have a simplified universe where all theorems of ZFC remain true and the properties like randomness are efficiently defined with respect to the universe. There are in general plenty of possibilities for the choice of a model describing the singular interior of BH; however, one is particularly distinguished. This is the countable minimal model $L_{\alpha }$ which has been shown by Benioff [10,11] to be strong enough to carry all the mathematics of QM and, at the same time, randomness of the sequences of outcomes of QM measurements should be found outside. We showed that they are in the random forcing extensions $L_{\alpha }\left[h_i\right]$’s and the derivation was based on the formal structure of QM.

Applying these findings to BHs and, assuming the change of the set universe to $L_{\alpha }$ containing the singularity, we also tested (heuristically) the model against the Beckenstein–Hawking entropy relation and found that it is retrieved in the model up to a (undetermined so far) constant. Next, we analyzed the computational complexity realized in this model of BHs. The recent approach by Susskind et al. (e.g., [1,3]) estimates the computational complexity of the state spaces of BHs via quantum computing circuits and the measure of complexity are related to the entropy of BHs. We found the complexity based on the classical concepts of computing and randomness (see Section 3.2 and Theorem 1). However, the two approaches cannot be disjoint. The reason is that any conceivable construction of even the weakest 1-random infinite sequence requires QM and cannot be realized within the deterministic classical realm (e.g., [6]). This is why—when we showed that BHs in our approach require n-randomness classes, $n\ge 1$, by ‘classical’ means—the quantum realm comes back through the back doors as it should be when one thinks about BHs at the fundamental level. There exists a vast amount of literature regarding randomness and QM (see, e.g., [5]). However, the proposed by us, ZFC countable models point of view seems to be a promising alternative. It is worth emphasizing that a ZFC-based approach to QM has been already present in physics before (e.g., [10,11,22,23]) and—in a sense—our research continues these works.

Much remains to be done. Every fundamental version of QG should reproduce finiteness of the entropy and $1/4$ factor in the Beckenstein–Hawking law (B-H). For example, loop quantum gravity confirms finiteness and proportionality of entropy to the area of the horizon [24] and superstring theory supports the B-H law for some class of BHs, e.g., [25]. When we expect that the presented approach aims to be fundamental in some respect for QG (forcing extensions from the lattice $\mathbb{L}$ should survive in a successful version of QG), we should address the B-H precise formula in the model of BH explored here. We do not know how to achieve it now, though certain attempts are being performed. The relation of randomness and QM understood from the point of view of varying models of set theory can be pushed further—in particular toward better understanding of the measurement problem in QM and resulting randomness envisioned by the Born’s rule. Next, we included the recognition of the regime of quantum gravity based on the dynamical ZFC environment and the fundamental role assigned to gravitons and their ZFC counterparts. In addition, the points closer to those not resolved in this paper, like whether we can be sure that QM is in the model of ZFC—is this mandatory or just a formal possibility? What else in physics emerges from such eventual necessity (one would be the presented model of BHs)? The varying models of ZFC extend our toolkit toward studying the overlapping region of QM and classical spacetime touched here (and more extensively in [8])—the approach should be developed further. Connected with this is the modification of the smooth spacetime structure due to such overlapping with QM which also was signaled in [8,9]. The issue of independence of the results in the previous section on the choice of a model of ZFC and the role of infinite dimensional Hilbert space of states in such fundamental approaches should be further explained. Finally, is QM random, 1-random, 2-random, or $\omega$-random in a sense that it could be tested experimentally? Infinite random binary sequences are (or are not) random but, even mathematically, to prove that a single such sequence is random belongs to formally undecidable problems—let alone how to recognize from finite parts of random sequences their randomness as an infinite ones by experimental means. The experimental grasping, along with theoretical understanding, of these kinds of problems within QM is important for designing and manipulating the true random sequences in practice (e.g., [26]). Most of the issues raised above will be addressed in our forthcoming publication [17].