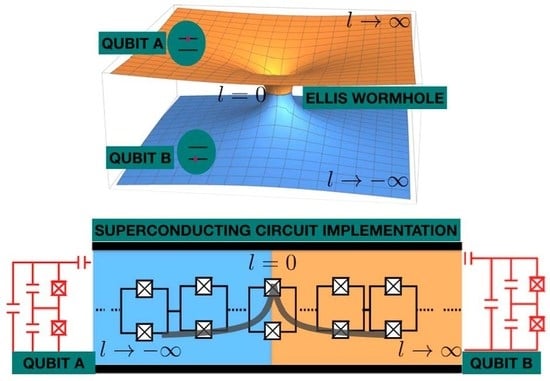
Entangling Superconducting Qubits through an Analogue Wormhole
Abstract
:1. Introduction
2. Model and Results
3. Conclusions
Funding
Conflicts of Interest
References
- Summers, S.J.; Werner, R.F. The vacuum violates Bell’s inequalities. Phys. Lett. A 1985, 110, 257–259. [Google Scholar] [CrossRef]
- Summers, S.J.; Werner, R.F. Bell’s inequalities and quantum field theory. II. Bell’s inequalities are maximally violated in the vacuum. J. Math. Phys. 1987, 28, 2448. [Google Scholar] [CrossRef]
- Moore, G.T. Quantum Theory of the Electromagnetic Field in a Variable-Length One-Dimensional Cavity. J. Math. Phys. 1970, 11, 2679–2691. [Google Scholar] [CrossRef]
- Fulling, S.A. Nonuniqueness of canonical field quantization in Riemannian space-time. Phys. Rev. D 1973, 7, 2850–2862. [Google Scholar] [CrossRef]
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Davies, P. Scalar production in Schwarzschild and Rindler metrics. J. Phys. A 1975, 8, 609. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef] [Green Version]
- Bell, J.S.; Leinaas, J.M. Electrons as accelerated thermometers. Nucl. Phys. B 1983, 212, 131. [Google Scholar] [CrossRef] [Green Version]
- Akhmedov, E.T.; Singleton, D. On the relation between Unruh and Sokolov–Ternov effects. Int. J. Mod. Phys. 2007, 22, 4797–4823. [Google Scholar] [CrossRef] [Green Version]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 2011, 479, 376–379. [Google Scholar] [CrossRef]
- Johansson, J.R.; Johansson, G.; Wilson, C.M.; Delsing, P.; Nori, F. Nonclassical microwave radiation from the dynamical Casimir effect. Phys. Rev. A 2013, 87, 043804. [Google Scholar] [CrossRef] [Green Version]
- Sabín, C.; Fuentes, I.; Johansson, G. Quantum discord in the dynamical Casimir effect. Phys. Rev. A 2015, 92, 012314. [Google Scholar] [CrossRef] [Green Version]
- Sabín, C.; Adesso, G. Generation of quantum steering and interferometric power in the dynamical Casimir effect. Phys. Rev. A 2015, 92, 042107. [Google Scholar] [CrossRef] [Green Version]
- De Buruaga, D.N.S.S.; Sabín, C. Quantum coherence in the dynamical Casimir effect. Phys. Rev. A 2017, 95, 022307. [Google Scholar] [CrossRef] [Green Version]
- Felicetti, S.; Sanz, M.; Lamata, L.; Romero, G.; Johansson, G.; Delsing, P.; Solano, E. Dynamical Casimir effect entangles artificial atoms. Phys. Rev. Lett. 2014, 113, 093602. [Google Scholar] [CrossRef] [Green Version]
- Reznik, B.; Retzker, A.; Silman, J. Violating Bell’s inequalities in vacuum. Phys. Rev. A 2005, 71, 042104. [Google Scholar] [CrossRef] [Green Version]
- Retzker, A.; Cirac, J.I.; Reznik, B. Detecting vacuum entanglement in a linear ion trap. Phys. Rev. Lett. 2005, 94, 050504. [Google Scholar] [CrossRef] [Green Version]
- Sabín, C.; García-Ripoll, J.J.; Solano, E.; León, J. Dynamics of entanglement via propagating microwave photons. Phys. Rev. B 2010, 81, 184501. [Google Scholar] [CrossRef] [Green Version]
- Sabín, C.; Peropadre, B.; del Rey, M.; Martín-Martínez, E. Extracting past-future vacuum correlations using circuit QED. Phys. Rev. Lett. 2012, 109, 033602. [Google Scholar] [CrossRef] [Green Version]
- Alsing, P.M.; Fuentes, I. Observer-dependent entanglement. Class. Quantum Gravity 2012, 29, 224001. [Google Scholar] [CrossRef] [Green Version]
- Ng, K.K.; Mann, R.B.; Martín-Martínez, E. New techniques for entanglement harvesting in flat and curved spacetimes. Phys. Rev. D 2018, 97, 125011. [Google Scholar] [CrossRef] [Green Version]
- Henderson, L.J.; Hennigar, R.A.; Mann, R.B.; Smith, A.R.H.; Zhang, J. Harvesting entanglement from the black hole vacuum. Class. Quantum Gravity 2018, 35, 21LT02. [Google Scholar] [CrossRef] [Green Version]
- Ng, K.K.; Mann, R.B.; Martín-Martínez, E. Unruh-DeWitt detectors and entanglement: The anti–de Sitter space. Phys. Rev. D 2018, 98, 125005. [Google Scholar] [CrossRef] [Green Version]
- Barceló, C.; Liberati, S.; Visser, M. Analogue gravity. Living Rev. Relativ. 2011, 14, 3. [Google Scholar] [CrossRef] [Green Version]
- Visser, M.; Molina-Paris, C. Acoustic geometry for general relativistic barotropic irrotational fluid flow. New J. Phys. 2010, 12, 095014. [Google Scholar] [CrossRef]
- Moncrief, V. Stability of stationary, spherical accretion onto a Schwarzschild black hole. Astrophys. J. 1980, 235, 1038–1046. [Google Scholar] [CrossRef]
- Ge, X.-H.; Nakahara, M.; Sin, S.-J.; Tian, Y.; Wu, S.-F. Acoustic black holes in curved spacetime and the emergence of analogue Minkowski spacetime. Phys. Rev. D 2019, 99, 104047. [Google Scholar] [CrossRef] [Green Version]
- Ge, X.-H.; Wu, S.-F.; Wang, Y.; Yang, G.-H.; Shen, Y.-G. Acoustic black holes from supercurrent tunneling. Int. J. Mod. Phys. D 2012, 21, 1250038. [Google Scholar] [CrossRef] [Green Version]
- Wallraff, A.; Schuster, D.; Blais, A.; Frunzio, L.; Huang, R.S.; Majer, J.; Kumar, S.; Girvin, S.M.; Schoelkopf, R.J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 431, 162–167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haroche, S.; Brune, M.; Raimond, J.M. From cavity to circuit quantum electrodynamics. Nature Phys. 2020, 16, 243–246. [Google Scholar] [CrossRef]
- Bourassa, J.; Gambetta, J.M.; Abdumalikov, A.A.; Astafiev, O.; Nakamura, Y.; Blais, A. Ultrastrong coupling regime of cavity QED with phase-biased flux qubits. Phys. Rev. A 2009, 80, 032109. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lisenfeld, J.; Marcos, D.; García-Ripoll, J.J.; Solano, E.; Harmans, C.J.P.M.; Mooij, J.E. Observation of the Bloch-Siegert shift in a qubit-oscillator system in the ultrastrong coupling regime. Phys. Rev. Lett. 2010, 105, 237001. [Google Scholar] [CrossRef] [Green Version]
- Peropadre, B.; Forn-Díaz, P.; Solano, E.; García-Ripoll, J.J. Switchable ultrastrong coupling in circuit QED. Phys. Rev. Lett. 2010, 105, 023601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niemczyk, T.; Deppe, F.; Huebl, H.; Menzel, E.P.; Hocke, F.; Schwarz, M.J.; Garcia-Ripoll, J.J.; Zueco, D.; Hümmer, T.; Solano, E.; et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 2010, 6, 772–776. [Google Scholar] [CrossRef] [Green Version]
- Forn-Díaz, P.; García-Ripoll, J.J.; Peropadre, B.; Orgiazzi, J.L.; Yurtalan, M.A.; Belyansky, R.; Wilson, C.M.; Lupascu, A. Ultrastrong coupling of a single artificial atom to an electromagnetic continuum in the nonperturbative regime. Nat. Phys. 2017, 13, 39–43. [Google Scholar] [CrossRef]
- Nation, P.D.; Johansson, J.R.; Blencowe, M.P.; Nori, F. Colloquium: Stimulating uncertainty: Amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 2012, 84, 1. [Google Scholar] [CrossRef] [Green Version]
- Ellis, H.G. Ether flow through a drainhole: A particle model in general relativity. J. Math. Phys. (N.Y.) 1973, 14, 104. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, time machines, and the weak energy condition. Phys. Rev. Lett. 1988, 61, 1446. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, R.; Asada, H. Observational upper bound on the cosmic abundances of negative-mass compact objects and Ellis wormholes from the Sloan digital sky survey quasar lens search. Astrophys. J. Lett. 2013, 768, L16. [Google Scholar] [CrossRef] [Green Version]
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef] [Green Version]
- Hawking, S.W. Chronology protection conjecture. Phys. Rev. D 1992, 46, 603. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, D. Quantum mechanics near closed timelike lines. Phys. Rev. D 1991, 44, 3197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ford, L.H.; Roman, T.A. Averaged energy conditions and quantum inequalities. Phys. Rev. D 1995, 51, 4277. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cardoso, V.; Franzin, E.; Pani, P. Erratum: Is the Gravitational-Wave Ringdown a Probe of the Event Horizon? Phys. Rev. Lett. 2016, 116, 171101. [Google Scholar] [CrossRef] [PubMed]
- Konoplya, R.A.; Zhidenko, A. Wormholes versus black holes: Quasinormal ringing at early and late times. J. Cosmol. Astropart. Phys. 2016, 12, 043. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Bambi, C. Distinguishing black holes and wormholes with orbiting hot spots. Phys. Rev. D 2014, 90, 024071. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X.; Assad, S.M.; Thompson, J.; Haw, J.Y.; Vedral, V.; Ralph, T.C.; Lam, P.K.; Weedbrook, C.; Gu, M. Replicating the benefits of closed timelike curves without breaking causality. Npj Quantum Inf. 2015, 1, 15007. [Google Scholar] [CrossRef] [Green Version]
- Maldacena, J.; Susskind, L. Cool horizons for entangled black holes. Fortschr. Phys. 2013, 61, 781–811. [Google Scholar] [CrossRef] [Green Version]
- Müller, T. Exact geometric optics in a Morris-Thorne wormhole spacetime. Phys. Rev. D 2008, 77, 044043. [Google Scholar] [CrossRef] [Green Version]
- Taylor, P. Propagation of test particles and scalar fields on a class of wormhole space-times. Phys. Rev. D 2014, 90, 024057. [Google Scholar] [CrossRef] [Green Version]
- Sabín, C. Mapping curved spacetimes into Dirac spinors. Sci. Rep. 2017, 7, 40346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abe, F. Gravitational microlensing by the Ellis wormhole. Astrophys. J. 2010, 725, 787. [Google Scholar] [CrossRef]
- Nakajima, K.; Asada, H. Deflection angle of light in an Ellis wormhole geometry. Phys. Rev. D 2012, 85, 107501. [Google Scholar] [CrossRef] [Green Version]
- Ohgami, T.; Sakai, N. Wormhole shadows. Phys. Rev. D 2015, 91, 124020. [Google Scholar] [CrossRef] [Green Version]
- Sabín, C. Quantum detection of wormholes. Sci. Rep. 2017, 7, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanchidrián-Vaca, C.; Sabín, C. Parameter estimation of wormholes beyond the Heisenberg limit. Universe 2018, 4, 115. [Google Scholar] [CrossRef] [Green Version]
- Peloquin, C.; Euvé, L.P.; Philbin, T.; Rousseaux, G. Analog wormholes and black hole laser effects in hydrodynamics. Phys. Rev. D 2016, 93, 084032. [Google Scholar] [CrossRef] [Green Version]
- Euvé, L.P.; Rousseaux, G. Classical analogue of an interstellar travel through a hydrodynamic wormhole. Phys. Rev. D 2017, 96, 064042. [Google Scholar] [CrossRef] [Green Version]
- Prat-Camps, J.; Navau, C.; Sanchez, A. A magnetic wormhole. Sci. Rep. 2015, 5, 12488. [Google Scholar] [CrossRef]
- Sabín, C. Light propagation through nanophotonics wormholes. Universe 2018, 4, 137. [Google Scholar] [CrossRef] [Green Version]
- Sabín, C. Quantum simulation of traversable wormhole spacetimes in a dc-SQUID array. Phys. Rev. D 2016, 94, 081501. [Google Scholar] [CrossRef] [Green Version]
- Mateos, J.; Sabín, C. Quantum simulation of traversable wormhole spacetimes in a Bose-Einstein condensate. Phys. Rev. D 2018, 97, 044045. [Google Scholar] [CrossRef] [Green Version]
- Lähteenmäki, P.; Paraoanu, G.S.; Hassel, J.; Hakonen, P.J. Dynamical Casimir effect in a Josephson metamaterial. Proc. Natl. Acad. Sci. USA 2013, 110, 4234–4238. [Google Scholar] [CrossRef] [Green Version]
- Haviland, D.K.; Andersson, K.; Agren, P. Superconducting and insulating behavior in one-dimensional Josephson junction arrays. J. Low Temp. Phys. 2000, 118, 733–749. [Google Scholar] [CrossRef]
- Watanabe, M.; Haviland, D.B. Quantum effects in small-capacitance single Josephson junctions. Phys. Rev. B 2003, 67, 094505. [Google Scholar] [CrossRef] [Green Version]
- Ergül, A.; Schaeffer, D.; Lindblom, M.; Haviland, D.B.; Lidmar, J.; Johansson, J. Phase sticking in one-dimensional josephson junction chains. Phys. Rev. B 2013, 88, 104501. [Google Scholar] [CrossRef] [Green Version]
- Puertas Martínez, J.; Léger, S.; Gheeraert, N.; Dassonneville, R.; Planat, L.; Foroughi, F.; Krupko, Y.; Buisson, O.; Naud, C.; Hasch-Guichard, W.; et al. A Tunable Josephson Platform to Explore Many-Body Quantum Optics in Circuit-QED. Npj Quantum Inf. 2019, 5, 19. [Google Scholar] [CrossRef] [Green Version]
- Castellanos-Beltran, M.A.; Lehnert, K.W. Widely tunable parametric amplifier based on a superconducting quantum interference device array resonator. Appl. Phys. Lett. 2007, 91, 083509. [Google Scholar] [CrossRef] [Green Version]
- Sandbo Chang, C.W.; Sabín, C.; Forn-Díaz, P.; Quijandría, F.; Vadiraj, A.M.; Nsanzineza, I.; Johansson, G.; Wilson, C.M. Observation of Three-Photon Spontaneous Parametric Down-Conversion in a Superconducting Parametric Cavity. Phys. Rev. X 2020, 10, 011011. [Google Scholar]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabín, C. Entangling Superconducting Qubits through an Analogue Wormhole. Universe 2020, 6, 149. https://doi.org/10.3390/universe6090149
Sabín C. Entangling Superconducting Qubits through an Analogue Wormhole. Universe. 2020; 6(9):149. https://doi.org/10.3390/universe6090149
Chicago/Turabian StyleSabín, Carlos. 2020. "Entangling Superconducting Qubits through an Analogue Wormhole" Universe 6, no. 9: 149. https://doi.org/10.3390/universe6090149
APA StyleSabín, C. (2020). Entangling Superconducting Qubits through an Analogue Wormhole. Universe, 6(9), 149. https://doi.org/10.3390/universe6090149