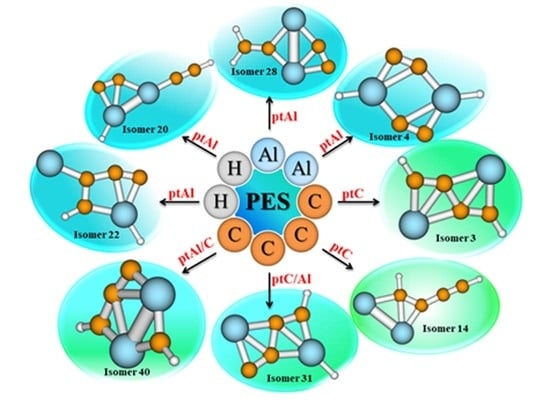
Al2C4H2 Isomers with the Planar Tetracoordinate Carbon (ptC)/Aluminum (ptAl)
Abstract
:1. Introduction
2. Computational Methodology
3. Results and Discussion
3.1. Wiberg Bond Indices
3.2. Topological Analysis
3.3. Kinetic Stability
3.4. Adaptive Natural Density Partitioning and Natural Bond Order Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AdNDP | Adaptive Natural Density Partitioning |
| ADMP | Atom-centered Density Matrix Propagation |
| DFT | Density Functional Theory |
| ELF | Electron Localization Function |
| NBO | Natural Bond Order |
| ON | Occupation Number |
| ptC | Planar Tetracoordinate Carbon |
| phC | Planar Hypercoordinate Carbon |
| ptAl | Planar Tetracoordinate Aluminum |
| ppAl | Planar Pentacoordinate Aluminum |
| WBI | Wiberg Bond Index |
| LP | Lone Pair |
References
- Leyva-Parra, L.; Inostroza, D.; Yañez, O.; Cruz, J.C.; Garza, J.; García, V.; Tiznado, W. Persistent Planar Tetracoordinate Carbon in Global Minima Structures of Silicon-Carbon Clusters. Atoms 2022, 10, 27. [Google Scholar] [CrossRef]
- Das, P.; Khatun, M.; Anoop, A.; Chattaraj, P.K. CSinGe4−n2+ (n = 1–3): Prospective Systems Containing Planar Tetracoordinate Carbon (PtC). Phys. Chem. Chem. Phys. 2022, 24, 16701–16711. [Google Scholar] [CrossRef]
- Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon Rings Decorated with Group 14 Elements: New Aromatic Clusters Containing Planar Tetracoordinate Carbon. New J. Chem. 2019, 43, 6781–6785. [Google Scholar] [CrossRef]
- Yang, L.M.; Ganz, E.; Chen, Z.; Wang, Z.X.; Schleyer, P.V.R. Four Decades of the Chemistry of Planar Hypercoordinate Compounds. Angew. Chem.-Int. Ed. 2015, 54, 9468–9501. [Google Scholar] [CrossRef]
- Merino, G.; Méndez-Rojas, M.A.; Beltrán, H.I.; Corminboeuf, C.; Heine, T.; Vela, A. Theoretical Analysis of the Smallest Carbon Cluster Containing a Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 2004, 126, 16160–16169. [Google Scholar] [CrossRef]
- Pancharatna, P.D.; Méndez-Rojas, M.A.; Merino, G.; Vela, A.; Hoffmann, R. Planar Tetracoordinate Carbon in Extended Systems. J. Am. Chem. Soc. 2004, 126, 15309–15315. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, B.; Zhai, H.; Zhou, R.; Ni, G.; Xu, Z. Mass Spectrometric and First Principles Study of AlnC− Clusters. Solid State Commun. 2002, 122, 543–547. [Google Scholar] [CrossRef] [Green Version]
- Jensen, C.M.; Gross, K.J. Development of Catalytically Enhanced Sodium Aluminum Hydride as a Hydrogen-Storage Material. Appl. Phys. A Mater. Sci. Process. 2001, 72, 213–219. [Google Scholar] [CrossRef]
- Leskiw, B.D.; Castleman, A.W. The Interplay between the Electronic Structure and Reactivity of Aluminum Clusters: Model Systems as Building Blocks for Cluster Assembled Materials. Chem. Phys. Lett. 2000, 316, 31–36. [Google Scholar] [CrossRef]
- Suresh, C.H.; Frenking, G. Direct 1−3 Metal−Carbon Bonding and Planar Tetracoordinated Carbon in Group 6 Metallacyclobutadienes. Organometallics 2010, 29, 4766–4769. [Google Scholar] [CrossRef]
- Ghana, P.; Rump, J.; Schnakenburg, G.; Arz, M.I.; Filippou, A.C. Planar Tetracoordinated Silicon (PtSi): Room-Temperature Stable Compounds Containing Anti-van’t Hoff/Le Bel Silicon. J. Am. Chem. Soc. 2021, 143, 420–432. [Google Scholar] [CrossRef]
- Ebner, F.; Greb, L. Calix [4]Pyrrole Hydridosilicate: The Elusive Planar Tetracoordinate Silicon Imparts Striking Stability to Its Anionic Silicon Hydride. J. Am. Chem. Soc. 2018, 140, 17409–17412. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhang, X.; Yu, S.; Ding, Y.H.; Bowen, K.H. Identifying the Hydrogenated Planar Tetracoordinate Carbon: A Combined Experimental and Theoretical Study of CAl4H and CAl4H−. J. Phys. Chem. Lett. 2017, 8, 2263–2267. [Google Scholar] [CrossRef] [Green Version]
- Keese, R. Carbon Flatland: Planar Tetracoordinate Carbon and Fenestranes. Chem. Rev. 2006, 106, 4787–4808. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.-F.; Wang, L.-S.; Geske, G.D.; Boldyrev, A.I. Pentaatomic Tetracoordinate Planar Carbon, [CAl4]2−: A New Structural Unit and Its Salt Complexes. Angew. Chem. 2000, 39, 3630–3632. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.S.; Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in the Al4C− Anion. A Combined Photoelectron Spectroscopy and Ab Initio Study. J. Am. Chem. Soc. 1999, 121, 6033–6038. [Google Scholar] [CrossRef]
- Boldyrev, A.I.; Simons, J. Tetracoordinated Planar Carbon in Pentaatomic Molecules. J. Am. Chem. Soc. 1998, 120, 7967–7972. [Google Scholar] [CrossRef]
- Erker, G. Planar-Tetracoordinate Carbon: Making Stable Anti-van’t Hoff/LeBel Compounds. Comments Inorg. Chem. 1992, 13, 111–131. [Google Scholar] [CrossRef]
- Cotton, F.A.; Millar, M. The Probable Existence of a Triple Bond between Two Vanadium Atoms. J. Am. Chem. Soc. 1977, 99, 7886–7891. [Google Scholar] [CrossRef]
- Röttger, D.; Erker, G. Compounds Containing Planar-Tetracoordinate Carbon. Angew. Chem. Int. Ed. Eng. 1997, 36, 812–827. [Google Scholar] [CrossRef]
- Van’t Hoff, J.H. A Suggestion Looking To the Extension Into Space of the Structural Formulas At Present Used in Chemistry. and a Note Upon the Relation Between the Optical Activity and the Chemical Constitution of Organic Compounds. Arch. Neerl. Des Sci. Exactes Nat. 1874, 9, 445–454. [Google Scholar]
- Le Bel, J.A. On the Relations Which Exist between the Atomic Formulas of Organic Compounds and the Rotatory Power of Their Solutions. Bull. Soc. Chim. Fr. 1874, 22, 337–347. [Google Scholar]
- Vassilev-Galindo, V.; Pan, S.; Donald, K.J.; Merino, G. Planar Pentacoordinate Carbons. Nat. Rev. Chem. 2018, 2, 0114. [Google Scholar] [CrossRef]
- Monkhorst, J.H. Activation Energy for Interconversion of enantiomers containing an asymmetric carbon atom without breaking bonds. Chem. Commun. 1968, 1111–1112. [Google Scholar] [CrossRef]
- Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
- Collins, J.B.; Dill, J.D.; Jemmis, E.D.; Apeloig, Y.; Schleyer, P.V.R.; Collins, J.B.; Jemmis, E.D.; Schleyer, P.V.R.; Seeger, R.; Pople, J.A. Stabilization of Planar Tetracoordinate Carbon. J. Am. Chem. Soc. 1976, 98, 5419–5427. [Google Scholar] [CrossRef]
- Pei, Y.; An, W.; Ito, K.; Schleyer, P.V.R.; Xiao, C.Z. Planar Pentacoordinate Carbon in CAI5+: A Global Minimum. J. Am. Chem. Soc. 2008, 130, 10394–10400. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Schleyer, P.V.R.; Chen, Z. Al2C Monolayer: The Planar Tetracoordinate Carbon Global Minimum. Nanoscale 2014, 6, 10784–10791. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liao, Y.; Chen, Z. Be2C Monolayer with Quasi-Planar Hexacoordinate Carbons: A Global Minimum Structure. Angew. Chem.-Int. Ed. 2014, 53, 7248–7252. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Yakobson, B.I.; Guo, W. Two-Dimensional Tetragonal TiC Monolayer Sheet and Nanoribbons. J. Am. Chem. Soc. 2012, 134, 19326–19329. [Google Scholar] [CrossRef]
- Wu, X.; Pei, Y.; Zeng, X.C. B2C Graphene, Nanotubes, and Nanoribbons. Nano Lett. 2009, 9, 1577–1582. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, F.; Li, Y.; Chen, Z. Semi-Metallic Be5C2 Monolayer Global Minimum with Quasi-Planar Pentacoordinate Carbons and Negative Poisson’s Ratio. Nat. Commun. 2016, 7, 11488. [Google Scholar] [CrossRef]
- Wang, L.-S.; Boldyrev, A.I.; Li, X.; Simons, J. Experimental Observation of Pentaatomic Tetracoordinate Planar Carbon-Containing Molecules. J. Am. Chem. Soc. 2000, 122, 7681–7687. [Google Scholar] [CrossRef]
- Zhai, H.J.; Wang, L.S.; Alexandrova, A.N.; Boldyrev, A.I. Electronic Structure and Chemical Bonding of B5− and B5 by Photoelectron Spectroscopy and Ab Initio Calculations. J. Chem. Phys. 2002, 117, 7917–7924. [Google Scholar] [CrossRef]
- Wang, L.M.; Huang, W.; Averkiev, B.B.; Boldyrev, A.I.; Wang, L.S. CB7−: Experimental and Theoretical Evidence against Hypercoordinate Planar Carbon. Angew. Chem.-Int. Ed. 2007, 46, 4550–4553. [Google Scholar] [CrossRef]
- Averkiev, B.B.; Zubarev, D.Y.; Wang, L.M.; Huang, W.; Wang, L.S.; Boldyrev, A.I. Carbon Avoids Hypercoordination in CB6−, CB62−, and C2B5− Planar Carbon-Boron Clusters. J. Am. Chem. Soc. 2008, 130, 9248–9250. [Google Scholar] [CrossRef]
- Dong, F.; Heinbuch, S.; Xie, Y.; Rocca, J.J.; Bernstein, E.R. Experimental and Theoretical Study of Neutral AlmCn and AlmCnHx Clusters. Phys. Chem. Chem. Phys. 2010, 12, 2569–2581. [Google Scholar] [CrossRef]
- Sergeeva, A.P.; Piazza, Z.A.; Romanescu, C.; Li, W.L.; Boldyrev, A.I.; Wang, L.S. B22− and B23−: All-Boron Analogues of Anthracene and Phenanthrene. J. Am. Chem. Soc. 2012, 134, 18065–18073. [Google Scholar] [CrossRef]
- Zhang, C.-J.; Wang, P.; Xu, X.-L.; Xu, H.-G.; Zheng, W.-J. Photoelectron Spectroscopy and Theoretical Study of AlnC5−/0 (n = 1–5) Clusters: Structural Evolution, Relative Stability of Star-like Clusters, and Planar Tetracoordinate Carbon Structures. Phys. Chem. Chem. Phys. 2021, 23, 1967–1975. [Google Scholar] [CrossRef]
- Wu, Y.-B.; Lu, H.-G.; Li, S.-D.; Wang, Z.-X. Simplest Neutral Singlet C2E4 (E = Al, Ga, In, and Tl) Global Minima with Double Planar Tetracoordinate Carbons: Equivalence of C2 Moieties in C2E4 to Carbon Centers in CAl42− and CAl5+. J. Phys. Chem. A 2009, 113, 3395–3402. [Google Scholar] [CrossRef]
- Wu, Y.B.; Jiang, J.L.; Lu, H.G.; Wang, Z.X.; Perez-Peralta, N.; Islas, R.; Contreras, M.; Merino, G.; Wu, J.I.C.; Von Ragué Schleyer, P. Starlike Aluminum-Carbon Aromatic Species. Chem. Eur. J. 2011, 17, 714–719. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.B.; Ding, Y.H. C Al4 X (X=Si,Ge): Molecules with Simultaneous Planar Tetracoordinate Carbon, Aluminum, and Silicon/Germanium. J. Chem. Phys. 2007, 126, 184302. [Google Scholar] [CrossRef] [PubMed]
- Irving, B.J.; Naumkin, F.Y. Communication: A Density Functional Investigation of Structure-Property Evolution in the Tetrakis Hexahedral C4Al14 Nanocluster. J. Chem. Phys. 2014, 141, 131102. [Google Scholar] [CrossRef] [PubMed]
- Boldyrev, A.I.; Simons, J.; Li, X.; Wang, L. Photoelectron Spectroscopy and Ab Initio Study. J. Am. Chem. Soc. 1999, 121, 10193–10197. [Google Scholar] [CrossRef]
- Zhang, C.; Dai, W.; Xu, H.; Xu, X.; Zheng, W. Structural Evolution of Carbon-Doped Aluminum Clusters AlnC− (n = 6–15): Anion Photoelectron Spectroscopy and Theoretical Calculations. J. Phys. Chem. A 2022, 126, 5621–5631. [Google Scholar] [CrossRef] [PubMed]
- Naumkin, F.Y. Flat-Structural Motives in Small Alumino−Carbon Clusters CnAlm (n = 2−3, m = 2−8). J. Phys. Chem. A 2008, 112, 4660–4668. [Google Scholar] [CrossRef]
- Das, P.; Chattaraj, P.K. CSiGaAl2−/0 and CGeGaAl2−/0 Having Planar Tetracoordinate Carbon Atoms in Their Global Minimum Energy Structures. J. Comput. Chem. 2022, 43, 894–905. [Google Scholar] [CrossRef] [PubMed]
- Maatallah, M.; Guo, M.; Cherqaoui, D.; Jarid, A.; Liebman, J.F. Aluminium Clusters for Molecular Hydrogen Storage and the Corresponding Alanes as Fuel Alternatives: A Structural and Energetic Analysis. Int. J. Hydrogen Energy 2013, 38, 5758–5767. [Google Scholar] [CrossRef]
- Dai, J.; Wu, X.; Yang, J.; Zeng, X.C. AlxC Monolayer Sheets: Two-Dimensional Networks with Planar Tetracoordinate Carbon and Potential Applications as Donor Materials in Solar Cell. J. Phys. Chem. Lett. 2014, 5, 2058–2065. [Google Scholar] [CrossRef]
- Job, N.; Khatun, M.; Thirumoorthy, K.; CH, S.S.R.; Chandrasekaran, V.; Anoop, A.; Thimmakondu, V.S. CAl4Mg0/−: Global Minima with a Planar Tetracoordinate Carbon Atom. Atoms 2021, 9, 24. [Google Scholar] [CrossRef]
- Khatun, M.; Roy, S.; Giri, S.; CH, S.S.R.; Anoop, A.; Thimmakondu, V.S. BAl4Mg−/0/+: Global Minima with a Planar Tetracoordinate or Hypercoordinate Boron Atom. Atoms 2021, 9, 89. [Google Scholar] [CrossRef]
- Georgakilas, V.; Tiwari, J.N.; Kemp, K.C.; Perman, J.A.; Bourlinos, A.B.; Kim, K.S.; Zboril, R. Noncovalent Functionalization of Graphene and Graphene Oxide for Energy Materials, Biosensing, Catalytic, and Biomedical Applications. Chem. Rev. 2016, 116, 5464–5519. [Google Scholar] [CrossRef]
- A/RES/71/313. Available online: https://web.archive.org/web/20201128194012/https://undocs.org/A/RES/71/313 (accessed on 7 October 2022).
- Tian, Y.H.; Hu, S.; Sheng, X.; Duan, Y.; Jakowski, J.; Sumpter, B.G.; Huang, J. Non-Transition-Metal Catalytic System for N2 Reduction to NH3: A Density Functional Theory Study of Al-Doped Graphene. J. Phys. Chem. Lett. 2018, 9, 570–576. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Zhang, D.; Sun, W.; Han, Z.; Liu, C. A Novel Aluminum-Doped Carbon Nanotubes Sensor for Carbon Monoxide. J. Mol. Struct. THEOCHEM 2007, 806, 93–97. [Google Scholar] [CrossRef]
- Dai, J.; Yuan, J.; Giannozzi, P. Gas Adsorption on Graphene Doped with B, N, Al, and S: A Theoretical Study. Appl. Phys. Lett. 2009, 95, 232105. [Google Scholar] [CrossRef]
- Compaan, K.R.; Agarwal, J.; Dye, B.E.; Yamaguchi, Y.; Schaefer, H.F. Toward Detection of AlCH2 and AlCH2+ in the Interstellar Medium. Astrophys. J. 2013, 778, 125–130. [Google Scholar] [CrossRef]
- Janczyk, A.; Ziurys, L.M. Laboratory Detection and Pure Rotational Spectrum of AlSH (X∼1A’). Astrophys. J. 2006, 639, L107–L110. [Google Scholar] [CrossRef] [Green Version]
- Yousefi, M.; Bernath, P.F. Line Lists for AlF and AlCl in the X 1Σ+ Ground State. Astrophys. J. Suppl. Ser. 2018, 237, 8. [Google Scholar] [CrossRef] [Green Version]
- Hedderich, H.G.; Dulick, M.; Bernath, P.F. High Resolution Emission Spectroscopy of AlCl at 20 μ. J. Chem. Phys. 1993, 99, 8363–8370. [Google Scholar] [CrossRef]
- Hoeft, J.; Lovas, F.J.; Tiemann, E.; Törring, T. Microwave Absorption Spectra of AlF, GaF, InF, and TIF. Z. Naturforsch. A 1970, 25, 1029–1035. [Google Scholar] [CrossRef]
- Tenenbaum, E.D.; Ziurys, L.M. Exotic Metal Molecules in Oxygen-Rich Envelopes: Detection of AlOH (X 1Σ+) in VY Canis Majoris. Astrophys. J. Lett. 2010, 712, 93–97. [Google Scholar] [CrossRef] [Green Version]
- Walker, K.A.; Gerry, M.C. Laboratory Microwave Spectroscopy of Aluminium Cyanide. Chem. Phys. Lett. 1999, 301, 200–204. [Google Scholar] [CrossRef]
- Ma, B.; Yamaguchi, Y.; Schaefer, H.F. Spectroscopic Constants and Potential Energy Surfaces for the Possible Interstellar Molecules A1NC and A1CN. Mol. Phys. 1995, 86, 1331–1337. [Google Scholar] [CrossRef]
- Ziurys, L.M.; Savage, C.; Highberger, J.L.; Apponi, A.J.; Guélin, M.; Cernicharo, J. More Metal Cyanide Species: Detection of AlNC (X 1Σ+) toward IRC +10216. Astrophys. J. 2002, 564, L45–L48. [Google Scholar] [CrossRef]
- Tenenbaum, E.D.; Ziurys, L.M. Millimeter Detection of Alo (X 2Σ+): Metal Oxide Chemistry in the Envelope of VY Canis Majoris. Astrophys. J. 2009, 694, 59–63. [Google Scholar] [CrossRef]
- Kamiński, T.; Müller, H.S.P.; Schmidt, M.R.; Cherchneff, I.; Wong, K.T.; Brünken, S.; Menten, K.M.; Winters, J.M.; Gottlieb, C.A.; Patel, N.A. An Observational Study of Dust Nucleation in Mira (o Ceti). Astron. Astrophys. 2017, 599, A59. [Google Scholar] [CrossRef] [Green Version]
- Gobrecht, D.; Plane, J.M.C.; Bromley, S.T.; Decin, L.; Cristallo, S.; Sekaran, S. Bottom-up Dust Nucleation Theory in Oxygen-Rich Evolved Stars I. Aluminium Oxide Clusters. Astron. Astrophys. 2021, 658, A167. [Google Scholar] [CrossRef]
- Kramers, J.D.; Belyanin, G.A.; Przybyłowicz, W.J.; Winkler, H.; Andreoli, M.A.G. The Chemistry of the Extraterrestrial Carbonaceous Stone “Hypatia”: A Perspective on Dust Heterogeneity in Interstellar Space. Icarus 2022, 382, 115043. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-Row Elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [Green Version]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural Population Analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. ”Developing Paradigms of Chemical Bonding: Adaptive Natural Density Partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207. [Google Scholar] [CrossRef] [PubMed]
- Zubarev, D.Y.; Boldyrev, A.I. Revealing Intuitively Assessable Chemical Bonding Patterns in Organic Aromatic Molecules via Adaptive Natural Density Partitioning. J. Org. Chem. 2008, 73, 9251–9258. [Google Scholar] [CrossRef] [PubMed]
- Glendening, E.D.; Weinhold, F. Natural Resonance Theory: I. General Formalism. J. Comput. Chem. 1998, 19, 593–609. [Google Scholar] [CrossRef]
- Von Ragué Schleyer, P.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A Simple Measure of Electron Localization in Atomic and Molecular Systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Schlegel, H.B.; Millam, J.M.; Iyengar, S.S.; Voth, G.A.; Daniels, A.D.; Scuseria, G.E.; Frisch, M.J. Ab Initio Molecular Dynamics: Propagating the Density Matrix with Gaussian Orbitals. J. Chem. Phys. 2001, 114, 9758–9763. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malhan, A.H.; Sobinson, S.; Job, N.; Shajan, S.; Mohanty, S.P.; Thimmakondu, V.S.; Thirumoorthy, K. Al2C4H2 Isomers with the Planar Tetracoordinate Carbon (ptC)/Aluminum (ptAl). Atoms 2022, 10, 112. https://doi.org/10.3390/atoms10040112
Malhan AH, Sobinson S, Job N, Shajan S, Mohanty SP, Thimmakondu VS, Thirumoorthy K. Al2C4H2 Isomers with the Planar Tetracoordinate Carbon (ptC)/Aluminum (ptAl). Atoms. 2022; 10(4):112. https://doi.org/10.3390/atoms10040112
Chicago/Turabian StyleMalhan, Abdul Hamid, Sony Sobinson, Nisha Job, Shilpa Shajan, Surya Prakash Mohanty, Venkatesan S. Thimmakondu, and Krishnan Thirumoorthy. 2022. "Al2C4H2 Isomers with the Planar Tetracoordinate Carbon (ptC)/Aluminum (ptAl)" Atoms 10, no. 4: 112. https://doi.org/10.3390/atoms10040112
APA StyleMalhan, A. H., Sobinson, S., Job, N., Shajan, S., Mohanty, S. P., Thimmakondu, V. S., & Thirumoorthy, K. (2022). Al2C4H2 Isomers with the Planar Tetracoordinate Carbon (ptC)/Aluminum (ptAl). Atoms, 10(4), 112. https://doi.org/10.3390/atoms10040112