Cobalt-Hydrogen Atomic and Ionic Collisional Data
Abstract
:1. Introduction
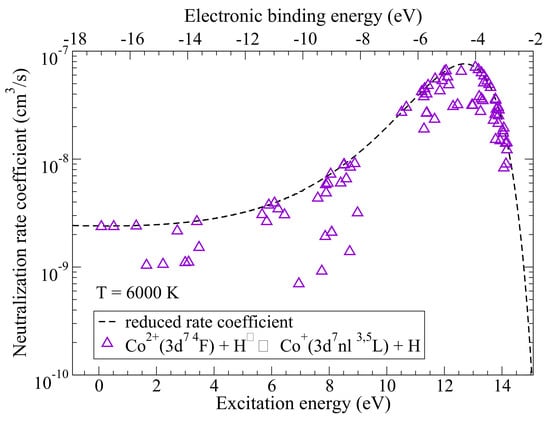
2. Inelastic Collisions with Hydrogen
3. Spectral Line Modelling
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| [H] LTE | Local Thermodynamic Equilibrium |
| NLTE | Non-Local Thermodynamic Equilibrium |
| SN | Supernova |
| dSph galaxy | dwarf spheroidal galaxy |
Appendix A
| j | Scattering Channels | Excitation Energy (eV) | Molecular Symmetries | |||
|---|---|---|---|---|---|---|
| 1 | 0.51548 | |||||
| 2 | 0.97685 | |||||
| 3 | 1.92787 | |||||
| 4 | 2.06497 | |||||
| 5 | 2.29594 | |||||
| 6 | 2.87577 | |||||
| 7 | 3.45747 | |||||
| 8 | 4.03969 | |||||
| 9 | 4.07631 | |||||
| 10 | 4.13694 | |||||
| 11 | 4.18423 | |||||
| 12 | 4.44203 | |||||
| 13 | 4.51371 | |||||
| 14 | 5.20406 | |||||
| 15 | 5.38114 | |||||
| 16 | 5.39327 | |||||
| 17 | 5.44509 | |||||
| 18 | 5.62102 | |||||
| 19 | 5.68931 | |||||
| 20 | 5.69145 | |||||
| 21 | 5.73759 | |||||
| 22 | 5.73428 | |||||
| 23 | 5.80502 | |||||
| 24 | 5.95449 | |||||
| 25 | 6.23651 | |||||
| 26 | 6.27376 | |||||
| 27 | 6.27806 | |||||
| 28 | 6.34547 | |||||
| 29 | 6.35225 | |||||
| 30 | 6.38987 | |||||
| 31 | 6.39093 | |||||
| 32 | 6.39638 | |||||
| 33 | 6.40229 | |||||
| 34 | 6.40499 | |||||
| 35 | 6.40948 | |||||
| 36 | 6.41068 | |||||
| 37 | 6.41689 | |||||
| 38 | 6.43021 | |||||
| 39 | 6.49858 | |||||
| 40 | 6.50516 | |||||
| 41 | 6.50548 | |||||
| 42 | 6.51886 | |||||
| 43 | 6.54802 | |||||
| 44 | 7.12701 | |||||
| j | Scattering Channels | Excitation Energy (eV) | Molecular Symmetries | |||
|---|---|---|---|---|---|---|
| 1 | 0.09833 | |||||
| 2 | 0.51548 | |||||
| 3 | 1.73285 | |||||
| 4 | 1.92787 | |||||
| 5 | 2.99786 | |||||
| 6 | 3.13938 | |||||
| 7 | 3.19854 | |||||
| 8 | 3.57441 | |||||
| 9 | 3.64148 | |||||
| 10 | 3.70284 | |||||
| 11 | 4.19102 | |||||
| 12 | 4.81956 | |||||
| 13 | 4.98902 | |||||
| 14 | 5.03644 | |||||
| 15 | 5.09679 | |||||
| 16 | 5.19581 | |||||
| 17 | 5.24427 | |||||
| 18 | 5.33119 | |||||
| 19 | 5.37206 | |||||
| 20 | 5.43392 | |||||
| 21 | 5.48224 | |||||
| 22 | 5.52998 | |||||
| 23 | 5.71331 | |||||
| 24 | 5.75952 | |||||
| 25 | 5.86199 | |||||
| 26 | 5.94217 | |||||
| 27 | 5.97552 | |||||
| 28 | 5.99915 | |||||
| 29 | 5.95034 | |||||
| 30 | 6.04469 | |||||
| 31 | 6.14320 | |||||
| 32 | 6.31054 | |||||
| 33 | 6.40304 | |||||
| 34 | 6.56348 | |||||
| 35 | 6.59929 | |||||
| 36 | 6.63201 | |||||
| 37 | 6.64847 | |||||
| 38 | 6.71229 | |||||
| 39 | 6.72580 | |||||
| 40 | 6.73166 | |||||
| 41 | 6.74361 | |||||
| 42 | 6.74639 | |||||
| 43 | 6.75237 | |||||
| 44 | 6.75635 | |||||
| 45 | 6.75759 | |||||
| 46 | 6.76313 | |||||
| 47 | 6.78897 | |||||
| 48 | 6.80010 | |||||
| 49 | 6.80463 | |||||
| 50 | 6.80604 | |||||
| 51 | 6.84015 | |||||
| 52 | 6.84726 | |||||
| 53 | 6.90793 | |||||
| 54 | 7.09831 | |||||
| 55 | 7.64209 | |||||
| j | Scattering Channels | Excitation Energy (eV) | Molecular Symmetries | |||
|---|---|---|---|---|---|---|
| 1 | 0.086424 | |||||
| 2 | 0.515088 | |||||
| 3 | 1.298194 | |||||
| 4 | 1.654634 | |||||
| 5 | 2.228192 | |||||
| 6 | 2.722395 | |||||
| 7 | 2.997467 | |||||
| 8 | 3.116769 | |||||
| 9 | 3.402627 | |||||
| 10 | 3.477810 | |||||
| 11 | 5.667889 | |||||
| 12 | 5.829194 | |||||
| 13 | 5.901901 | |||||
| 14 | 6.100510 | |||||
| 15 | 6.225915 | |||||
| 16 | 6.445432 | |||||
| 17 | 6.944416 | |||||
| 18 | 7.602664 | |||||
| 19 | 7.741586 | |||||
| 20 | 7.879665 | |||||
| 21 | 7.862606 | |||||
| 22 | 7.953864 | |||||
| 23 | 7.891881 | |||||
| 24 | 8.050841 | |||||
| 25 | 8.082848 | |||||
| 26 | 8.087312 | |||||
| 27 | 8.396528 | |||||
| 28 | 8.502082 | |||||
| 29 | 8.519635 | |||||
| 30 | 8.592569 | |||||
| 31 | 8.711866 | |||||
| 32 | 8.730561 | |||||
| 33 | 8.885763 | |||||
| 34 | 8.983867 | |||||
| 35 | 10.51110 | |||||
| 36 | 10.67719 | |||||
| 37 | 11.21252 | |||||
| 38 | 11.28284 | |||||
| 39 | 11.29226 | |||||
| 40 | 11.31398 | |||||
| 41 | 11.37796 | |||||
| 42 | 11.38589 | |||||
| 43 | 11.39005 | |||||
| 44 | 11.43308 | |||||
| 45 | 11.65906 | |||||
| 46 | 11.67783 | |||||
| 47 | 11.84426 | |||||
| 48 | 11.92089 | |||||
| 49 | 12.00107 | |||||
| 50 | 12.05815 | |||||
| 51 | 12.10782 | |||||
| 52 | 12.14754 | |||||
| 53 | 12.29916 | |||||
| 54 | 12.45811 | |||||
| 55 | 12.58565 | |||||
| 56 | 12.95788 | |||||
| 57 | 12.98524 | |||||
| 58 | 13.07439 | |||||
| 59 | 13.18202 | |||||
| 60 | 13.20781 | |||||
| 61 | 13.25611 | |||||
| 62 | 13.28528 | |||||
| 63 | 13.28759 | |||||
| 64 | 13.33463 | |||||
| 65 | 13.33582 | |||||
| 66 | 13.36719 | |||||
| 67 | 13.36727 | |||||
| 68 | 13.37434 | |||||
| 69 | 13.48653 | |||||
| 70 | 13.55333 | |||||
| 71 | 13.60331 | |||||
| 72 | 13.70424 | |||||
| 73 | 13.76361 | |||||
| 74 | 13.77133 | |||||
| 75 | 13.77746 | |||||
| 76 | 13.78461 | |||||
| 77 | 13.80566 | |||||
| 78 | 13.86608 | |||||
| 79 | 13.86966 | |||||
| 80 | 13.87937 | |||||
| 81 | 13.89417 | |||||
| 82 | 13.93904 | |||||
| 83 | 14.02330 | |||||
| 84 | 14.04457 | |||||
| 85 | 14.06266 | |||||
| 86 | 14.06367 | |||||
| 87 | 14.12532 | |||||
| 88 | 14.13858 | |||||
| 89 | 14.17252 | |||||
| 90 | 14.17256 | |||||
| 91 | 16.33040 | |||||
References
- Asplund, M. New Light on Stellar Abundance Analyses: Departures from LTE and Homogeneity. Ann. Rev. Astron. Astrophys. 2005, 43, 481. [Google Scholar] [CrossRef]
- Barklem, P.S. Accurate abundance analysis of late-type stars: Advances in atomic physics. Astron. Astrophys. Rev. 2016, 24, 9. [Google Scholar] [CrossRef] [Green Version]
- Belyaev, A.K.; Grosser, J.; Hahne, J.; Menzel, T. Ab initio cross sections for low-energy inelastic H + Na collisions. Phys. Rev. A 1999, 60, 2151–2158. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Barklem, P.S.; Dickinson, A.S.; Gadéa, F.X. Cross sections for low-energy inelastic H + Na collisions. Phys. Rev. A 2010, 81, 032706. [Google Scholar] [CrossRef]
- Croft, H.; Dickinson, A.S.; Gadéa, F.X. A theoretical study of mutual neutralization in Li+ + H− collisions. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 81–94. [Google Scholar] [CrossRef]
- Croft, H.; Dickinson, A.S.; Gadéa, F.X. Rate coefficients for the Li+/H− and Li−/H+ mutual neutralization reactions. MNRAS 1999, 304, 327–329. [Google Scholar] [CrossRef] [Green Version]
- Belyaev, A.K.; Barklem, P.S. Cross sections for low-energy inelastic H+Li collisions. Phys. Rev. A 2003, 68, 062703. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Barklem, P.S.; Spielfiedel, A.; Guitou, M.; Feautrier, N.; Rodionov, D.S.; Vlasov, D.V. Cross sections for low-energy inelastic Mg + H and Mg+ + H− collisions. Phys. Rev. A 2012, 85, 032704. [Google Scholar] [CrossRef]
- Guitou, M.; Spielfiedel, A.; Rodionov, D.S.; Yakovleva, S.A.; Belyaev, A.K.; Merle, T.; Thévenin, F.; Feautrier, N. Quantum chemistry and nuclear dynamics as diagnostic tools for stellar atmosphere modeling. Chem. Phys. 2015, 462, 94–103. [Google Scholar] [CrossRef]
- Belyaev, A.K. Excitation cross sections in low-energy hydrogen-helium collisions. Phys. Rev. A 2015, 91, 062709. [Google Scholar] [CrossRef]
- Mitrushchenkov, A.; Guitou, M.; Belyaev, A.K.; Yakovleva, S.A.; Spielfiedel, A.; Feautrier, N. Calcium-hydrogen interactions for collisional excitation and charge transfer. J. Chem. Phys. 2017, 146, 014304. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Vlasov, D.V.; Mitrushchenkov, A.; Feautrier, N. Quantum study of inelastic processes in low-energy calcium-hydrogen collisions. MNRAS 2019, 490, 3384–3391. [Google Scholar] [CrossRef]
- Stenrup, M.; Larson, A.; Elander, N. Mutual neutralization in low-energy H+ + H− collisions: A quantum ab initio study. Phys. Rev. A 2009, 79, 012713. [Google Scholar] [CrossRef]
- Nkambule, S.M.; Elander, N.; Larson, A.; Lecointre, J.; Urbain, X.; Larson, A.; Elander, N. Differential and total cross sections of mutual neutralization in low-energy collisions of isotopes of H+ + H−. Phys. Rev. A 2016, 93, 032701. [Google Scholar] [CrossRef]
- Drawin, H.W. Zur formelmäßigen Darstellung des Ionisierungsquerschnitts für den Atom-Atomstoß und über die Ionen-Elektronen-Rekombination im dichten Neutralgas. Z. Phys. A Hadron. Nucl. 1968, 211, 404–417. [Google Scholar] [CrossRef]
- Drawin, H.W. Validity conditions for local thermodynamic equilibrium. Z. Phys. 1969, 228, 99–119. [Google Scholar] [CrossRef]
- Steenbock, W.; Holweger, H. Statistical equilibrium of lithium in cool stars of different metallicity. Astron. Astrophys. 1984, 130, 319–323. [Google Scholar]
- Lambert, D.L. Quantitative stellar spectroscopy with large optical telescopes. Phys. Scr. 1993, T47, 186–198. [Google Scholar] [CrossRef]
- Barklem, P.S.; Belyaev, A.K.; Guitou, M.; Feautrier, N.; Gadéa, F.X.; Spielfiedel, A. On inelastic hydrogen atom collisions in stellar atmospheres. Astron. Astrophys. 2011, 530, A94. [Google Scholar] [CrossRef]
- Thielemann, F.K.; Fröhlich, C.; Hirschi, R.; Liebendörfer, M.; Dillmann, I.; Mocelj, D.; Rauscher, T.; Martinez-Pinedo, G.; Langanke, K.; Farouqi, K.; et al. Production of intermediate-mass and heavy nuclei. Prog. Part. Nucl. Phys. 2007, 59, 74–93. [Google Scholar] [CrossRef]
- Bergemann, M.; Pickering, J.C.; Gehren, T. NLTE analysis of CoI/CoII lines in spectra of cool stars with new laboratory hyperfine splitting constants. MNRAS 2010, 401, 1334–1346. [Google Scholar] [CrossRef]
- Battistini, C.; Bensby, T. The origin and evolution of the odd-Z iron-peak elements Sc, V, Mn, and Co in the Milky Way stellar disk. Astron. Astrophys. 2015, 577, A9. [Google Scholar] [CrossRef] [Green Version]
- Andrews, B.H.; Weinberg, D.H.; Schönrich, R.; Johnson, J.A. Inflow, Outflow, Yields, and Stellar Population Mixing in Chemical Evolution Models. Astrophys. J. 2017, 835, 224. [Google Scholar] [CrossRef]
- Côté, B.; O’Shea, B.W.; Ritter, C.; Herwig, F.; Venn, K.A. The Impact of Modeling Assumptions in Galactic Chemical Evolution Models. Astrophys. J. 2017, 835, 128. [Google Scholar] [CrossRef] [Green Version]
- Lomaeva, M.; Jönsson, H.; Ryde, N.; Schultheis, M.; Thorsbro, B. Abundances of disk and bulge giants from high-resolution optical spectra - III. Sc, V, Cr, Mn, Co, Ni. Astron. Astrophys. 2019, 625, A141. [Google Scholar] [CrossRef] [Green Version]
- Kirby, E.N.; Xie, J.L.; Guo, R.; Kovalev, M.; Bergemann, M. Catalog of Chromium, Cobalt, and Nickel Abundances in Globular Clusters and Dwarf Galaxies. Astrophys. J. Suppl. Ser. 2018, 237, 18. [Google Scholar] [CrossRef] [Green Version]
- Kirby, E.N.; Xie, J.L.; Guo, R.; de los Reyes, M.A.C.; Bergemann, M.; Kovalev, M.; Shen, K.J.; Piro, A.L.; McWilliam, A. Evidence for Sub-Chandrasekhar Type Ia Supernovae from Stellar Abundances in Dwarf Galaxies. Astrophys. J. 2019, 881, 45. [Google Scholar] [CrossRef] [Green Version]
- Belyaev, A.K.; Yakovleva, S.A. Estimating Inelastic Heavy-Particle-Hydrogen Collision Data. I. Simplified Model and Application to Potassium-Hydrogen Collisions. Astron. Astrophys. 2017, 606, A147. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Yakovleva, S.A. Estimating Inelastic Heavy-Particle-Hydrogen Collision Data. II. Simplified Model for Ionic Collisions and Application to Barium-Hydrogen Ionic Collisions. Astron. Astrophys. 2017, 608, A33. [Google Scholar] [CrossRef] [Green Version]
- Olson, R.E.; Smith, F.T.; Bauer, E. Estimation of the Coupling Matrix Elements for One-Electron Transfer Systems. Appl. Opt. 1971, 10, 1848. [Google Scholar] [CrossRef]
- Belyaev, A.K. Model approach for low-energy inelastic atomic collisions and application to Al+H and Al+ + H−. Phys. Rev. A 2013, 88, 052704. [Google Scholar] [CrossRef]
- Landau, L. Zur Theorie der Energieübertragung bei Stroessen. Phys. Z. Sowietunion 1932, 1, 88–98. [Google Scholar]
- Landau, L. Zur Theorie der Energieübertragung bei Stroessen. II. Phys. Z. Sowietunion 1932, 2, 46–51. [Google Scholar]
- Zener, C. Non-Adiabatic Crossing of Energy Levels. Proc. Roy. Soc. A 1932, 137, 696–702. [Google Scholar] [CrossRef]
- Belyaev, A.K.; Lebedev, O.V. Nonadiabatic nuclear dynamics of atomic collisions based on branching classical trajectories. Phys. Rev. A 2011, 84, 014701. [Google Scholar] [CrossRef]
- Yakovleva, S.A.; Belyaev, A.K.; Kraemer, W.P. Inelastic processes in low-energy iron-hydrogen collisions. Chem. Phys. 2018, 515, 369–374. [Google Scholar] [CrossRef]
- Yakovleva, S.A.; Belyaev, A.K.; Kraemer, W.P. Inelastic processes in low-energy collisions of singly ionized iron with hydrogen atoms. MNRAS 2019, 483, 5105–5109. [Google Scholar] [CrossRef]
- Barklem, P.S.; Belyaev, A.K.; Asplund, M. Inelastic H + Li and H− + Li+ collisions and non-LTE Li I line formation in stellar atmospheres. Astron. Astrophys. 2003, 409, L1–L4. [Google Scholar] [CrossRef] [Green Version]
- Lind, K.; Asplund, M.; Barklem, P.S.; Belyaev, A.K. Non-LTE Calculations for Neutral Na in Late-Type Stars Using Improved Atomic Data. Astron. Astrophys. 2011, 528, A103. [Google Scholar] [CrossRef] [Green Version]
- Mashonkina, L.; Sitnova, T.; Belyaev, A.K. Influence of Inelastic Collisions with Hydrogen Atoms on the Non-LTE Modelling of Ca I and Ca II Lines in Late-Type Stars. Astron. Astrophys. 2017, 605, A53. [Google Scholar] [CrossRef] [Green Version]
- Belyaev, A.K.; Voronov, Y.V. Inelastic Processes in Low-energy Sulfur–Hydrogen Collisions. Astrophys. J. 2020, 893, 59. [Google Scholar] [CrossRef]
- Domcke, W. Theory of resonance and threshold effects in electron-molecule collisions: The projection- operator approach. Phys. Rep. 1991, 208, 97. [Google Scholar] [CrossRef]
- Grupp, F. MAFAGS-OS: New opacity sampling model atmospheres for A, F and G stars. I. The model and the solar flux. Astron. Astrophys. 2004, 420, 289–305. [Google Scholar] [CrossRef] [Green Version]
- Grupp, F. MAFAGS-OS: New opacity sampling model atmospheres for A, F and G stars. II. Temperature determination and three “standard” stars. Astron. Astrophys. 2004, 426, 309–322. [Google Scholar] [CrossRef]
- Butler, K.; Giddings, J. Newsletter on Analysis of Astronomical Spectra No. 9; University College London: London, UK, 1985. [Google Scholar]
- Reetz, J. Sauerstoff in Kühlen Sternen und die Chemische Entwicklung der Galaxis. Ph.D. Thesis, LMU, München, Germany, 1999. [Google Scholar]
- Belyaev, A.K.; Voronov, Y.V.; Yakovleva, S.A. Inelastic processes in calcium-hydrogen ionic collisions with account for fine structure. Phys. Rev. A 2019, 100, 062710. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Version 5.7.1). Available online: http://physics.nist.gov/asd (accessed on 18 October 2019).
Sample Availability: The calculated rate coefficients are available from the authors. |






| T | log(g) | [Fe/H] | V | NLTE Corrections | |||
|---|---|---|---|---|---|---|---|
| 4020 | 4110 | 4121 | 5369 | ||||
| 4500 | 2.00 | 0.00 | 2.00 | 0.02 | 0.06 | 0.01 | 0.04 |
| 4500 | 2.00 | −2.00 | 2.00 | 0.24 | 0.43 | 0.27 | 0.20 |
| 6000 | 4.00 | 0.00 | 1.00 | 0.06 | 0.09 | 0.06 | 0.09 |
| 6000 | 4.00 | −2.00 | 1.00 | 0.40 | 0.27 | 0.28 | 0.24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakovleva, S.A.; Belyaev, A.K.; Bergemann, M. Cobalt-Hydrogen Atomic and Ionic Collisional Data. Atoms 2020, 8, 34. https://doi.org/10.3390/atoms8030034
Yakovleva SA, Belyaev AK, Bergemann M. Cobalt-Hydrogen Atomic and Ionic Collisional Data. Atoms. 2020; 8(3):34. https://doi.org/10.3390/atoms8030034
Chicago/Turabian StyleYakovleva, Svetlana A., Andrey K. Belyaev, and Maria Bergemann. 2020. "Cobalt-Hydrogen Atomic and Ionic Collisional Data" Atoms 8, no. 3: 34. https://doi.org/10.3390/atoms8030034
APA StyleYakovleva, S. A., Belyaev, A. K., & Bergemann, M. (2020). Cobalt-Hydrogen Atomic and Ionic Collisional Data. Atoms, 8(3), 34. https://doi.org/10.3390/atoms8030034