Next Article in Journal
DLBCL Cells with Acquired Resistance to Venetoclax Are Not Sensitized to BIRD-2 But Can Be Resensitized to Venetoclax through Bcl-XL Inhibition
Next Article in Special Issue
Multivalent and Bidirectional Binding of Transcriptional Transactivation Domains to the MED25 Coactivator
Previous Article in Journal
POSCAbilities: The Application of the Prion Organotypic Slice Culture Assay to Neurodegenerative Disease Research
Previous Article in Special Issue
Sequence-Dependent Correlated Segments in the Intrinsically Disordered Region of ChiZ
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Biomolecules
Volume 10
Issue 7
10.3390/biom10071080
biomolecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

Analysis of Protein Disorder Predictions in the Light of a Protein Structural Alphabet

by
Alexandre G. de Brevern
INSERM, UMR_S 1134, DSIMB, Univ Paris, INTS, Laboratoire d’Excellence GR-Ex, 75015 Paris, France
Biomolecules 2020, 10(7), 1080; https://doi.org/10.3390/biom10071080
Submission received: 15 June 2020 / Revised: 14 July 2020 / Accepted: 18 July 2020 / Published: 20 July 2020
(This article belongs to the Special Issue Computational Perspectives on Intrinsic Disorder-Based Functionality)
Browse Figures
Versions Notes

Abstract

:
Intrinsically-disordered protein (IDP) characterization was an amazing change of paradigm in our classical sequence-structure-function theory. Moreover, IDPs are over-represented in major disease pathways and are now often targeted using small molecules for therapeutic purposes. This has had created a complex continuum from order-that encompasses rigid and flexible regions-to disorder regions; the latter being not accessible through classical crystallographic methodologies. In X-ray structures, the notion of order is dictated by access to resolved atom positions, providing rigidity and flexibility information with low and high experimental B-factors, while disorder is associated with the missing (non-resolved) residues. Nonetheless, some rigid regions can be found in disorder regions. Using ensembles of IDPs, their local conformations were analyzed in the light of a structural alphabet. An entropy index derived from this structural alphabet allowed us to propose a continuum of states from rigidity to flexibility and finally disorder. In this study, the analysis was extended to comparing these results to disorder predictions, underlying a limited correlation, and so opening new ideas to characterize and predict disorder.

Graphical Abstract

1. Introduction

Analyses of protein structures have been extensively done in light of classical repetitive secondary structures, namely the α-helices and the β-sheets, connected by loops [1]. Since the end of the 1980s, more complex structural alphabets (SAs) entirely describing protein structures, have been developed [2,3] and applied to multiple tasks e.g., protein superimposition [4,5,6], molecular dynamics analysis [7], binding site detections [8], flexibility prediction [9], or threading approaches [10,11]. In this field, protein blocks (PBs), structural alphabets have been particularly successful [12]. Recently, they have been used to analyze flexibility of protein structures [13,14] and molecular dynamics simulations [15], e.g., integrins [16], HIV-1 capsid protein [17], and the N-methyl-D-aspartate receptor (NMDA) receptor channel gate [18]. Nonetheless, all these studies did not look at an essential part of the proteins. They only focused on ordered regions.
Intrinsic disorder is characterized by lack of stable tertiary structure under physiological conditions [19]. Approximately 19% of residues in these proteins are disordered and essential for multiple cellular functions that involve protein-protein, protein-nucleic acid, and virus-host interactions [20]. The intrinsically-disordered proteins (IDPs) [21,22,23,24] do not have a well-defined 3-D structure but rather adopt an ensemble of conformations that are functional in solution [25]. IDPs exist as dynamic ensembles, within which atom positions and backbone angles exhibit random temporal fluctuations [26,27].
Both experimental and computational approaches have been used to address the questions of IDPs. Nuclear magnetic resonance (NMR) provides quantitative residue-level information on structure and dynamics of IDPs as structural ensembles [28]. Small-angle X-ray scattering (SAXS) and electron microscopy (EM) gives an in-situ ensemble model describing the conformational behavior of the disordered region. Molecular dynamics (MDs) is used to refine and propose such ensembles [29,30,31].
Another important point is that the classical sequence-structure-function dogma was questioned by these extremely fast movements and the rigid, flexible, and deformable dynamic states that it may acquire or lose [32,33], but is can be also be a patchwork of ordered and disordered regions [34].
Hence, within the analyses of flexibility in globular proteins, PBs were applied to an ensemble of structural models of IDPs, provided in a dedicated database named PED3 (Protein Ensemble Database) [35]. Using Neq, an entropy index derived from this structural alphabet, we underlined its interest to measure these local dynamics, and to quantify the continuum of states from rigidity to flexibility, and finally disorder. Non-disordered regions in the ensemble of disordered proteins were also underlined [36,37]. PBs had been efficiently used to highlight rigid local domains within flexible regions and so discriminate deformability and mobility concepts. To access IDP structural information is sometimes complex. A large number of prediction approaches exist. A remaining question was the question of the relationship between this new quantification and the quality of disorder prediction approaches. Indeed, through our different researches, rigid regions (i.e., mobile regions) were underlined between two flexible regions (i.e., deformable regions); these domains can be interpreted as disordered when they are not entirely disordered. This peculiarity can bias the prediction of disorder regions. In this study, two distinct prediction methodologies were used in this way and the correlation named Neq was evaluated.

2. Materials and Methods

2.1. Dataset

The IDP ensembles of structures were taken from Protein Ensemble Database (PED3). This database of conformational ensembles describes flexible proteins (http://pedb.vib.be/index.php, accessed on 25 May 2020) [35] and has 24 entries. The different IDPs came from different techniques, i.e., SAXS and NMR, NMR alone, SAXS alone and molecular dynamics [38,39,40,41,42,43,44,45,46,47,48] and have been analyzed in [36].

2.2. Neq Entropy Index

Protein blocks (PBs) are the most widely-used structural alphabet composed of 16 local prototypes [12]. It is employed to analyze local conformations of protein structures from the Protein Data Bank (PDB) [49] (see [3] for a review of the structural alphabet and [50] for information on PBs). Each PB is characterized by the φ and ψ dihedral angles of five consecutive residues. PBs give a reasonable approximation of all local protein 3D structures and are very efficient for analyzing protein flexibility, i.e., molecular dynamics (MDs) analyses [16,18,51]. PB assignment was carried out for every residue from every structure/structural model extracted from PED3 using the PBxplore tool [52]. To quantify local protein flexibility, PB-derived entropy measure Neq (equivalent number of PBs) [12] was used. It represents the average number of PBs a residue may adopt at a given position. Neq is calculated as follows [12]:
N e q = e x p ( − ∑ x = 1 16 f x l n f x )
where, fx is the frequency of PB x at the position of interest. Neq value can vary between 1 and 16. A Neq value of 1 indicates that only one type of PB is observed, while a value of 16 indicates an equal probability for each of the 16 PBs, i.e., random distribution.

2.3. Disorder Prediction from the Sequence

Two different approaches were initially used to predict protein disorder from the sole information of the sequence, namely Disopred3 (used through http://bioinf.cs.ucl.ac.uk/psipred/webserver) [53,54] and Protein DisOrder Prediction System (PrDOS, through http://prdos.hgc.jp/cgi-bin/top.cgi) [55], see [37]. Disopred3 combined two predictors of intrinsic disorder, one module that combined the intermediate results and one component that annotated protein-binding IDRs; their neural networks used evolutionary information encoded in a position-specific score matrix (PSSM) [53]. PrDOS also combined two separate predictors; the first one was a support vector machine algorithm using evolutionary information again with PSSMs. The second one assumed the conservation of intrinsic disorder in protein families [55]. Results were finally also compared to a physics-based approach. IUPred2A and ANCHOR2 were used [56]. IUPred2A used an energy estimation method at its core. This approach utilized a low-resolution statistical potential to characterize the tendencies of amino acid pairs to form contacts, observed in a collection of globular protein structures. ANCHOR2 followed the same principle for disordered binding regions [57].
A prediction rate was used in the analysis. This prediction rate used (a) the predicted state (order and disorder) taken directly from Disopred3 and PrDOS and (b) the ‘true’ state defined by Neq, i.e., if the Neq is lower that the threshold value, it is an order state while if it is higher, it is a disorder state.

2.4. Analyses

The analyses were done using Python programming language v.2.7.10 [58], and R software v.3.3.3 [59] while 3D visualization was done using MacPyMOL software v.1.7.2.2 [60,61]. Different correlations are calculated, they are all based on the use of values coming from Disopred3 and/or PrDOS (in a range from 0 to 1), or with Neq (in a range from 1 to 16), and all done with continuous values and not binary classes. A perfect correlation is equal to 1.0, while a value of 0 corresponds to an absence of correlation.

3. Results

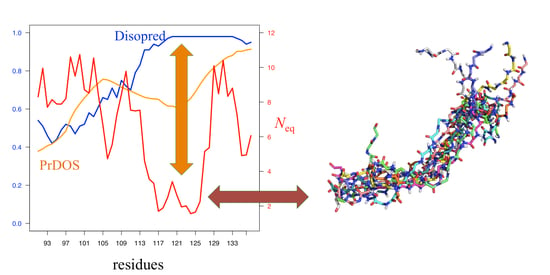
3.1. Data Analyses

The PED3 database encompasses an interesting set of structural behaviors. Figure 1A shows the Neq distribution. 58% of the positions are entirely rigid with a Neq of 1.0. In previous studies, we have analyzed ordered structures using a large dataset of molecular dynamics simulations. Hence, this number is equivalent to the one observed for ordered structures (60% for Neq of 1.0) [62]. However, these behaviors between order and disorder dataset evolved very rapidly. The disorder state had 36% of residues with an Neq higher 2 when it was only 8% for ordered structures. An Neq higher than 8 can be considered as entirely disordered state. The PED3 database had 15% of its residues with this feature while there were only 0.01% in ordered structures. The PED3 database allowed a very interesting continuum from rigidity to flexibility to high flexibility and finally disorder [36].
In protein structures obtained from X-ray crystallography, the definition of a disordered region can be considered as quite simple as it is linked to the absence of the atoms in a specific part of the sequence, i.e., they cannot be trapped as they are moving too fast [22]. Several physico-chemical and structural properties of intrinsic disorder are now well established (e.g., high net-charge and low hydrophobicity), and a large number of prediction methodologies use these physico-chemical properties linked with machine learning and evolutionary information [63,64].
Two distinct approaches were used to perform protein disorder predictions from the sole information of the protein sequences, (i) Disopred3 (Figure 1B) [53] and (ii) PrDOS (Figure 1C) [55].
The two distributions were quite different with more extreme values for Disopred3 and had a more centered distribution for PrDOS (Figure 1B,C). From their raw values, both methods also proposed the order/disorder two-states prediction, with 81.1% of predictions in common (32.9% of common disordered predicted positions and 48.2% of ordered ones). Disopred3 predicted more disordered positions (46.1%) than PrDOS (38.6%). They had a correct correlation of 0.75 in regard to the differences in the distribution of predicted values (Figure 2A).

3.2. Comparison of Neq with Prediction Results

As previously shown, analysis with local protein conformation is often different from global analysis. For instance, analyses of molecular dynamics simulation showed large difference between RMSf and Neq [13,16,18,65], with the correlation being slightly higher than 0.4. Therefore, the correlation between Neq and the prediction values was not expected to be much better. Moreover, the distributions of both structural information (namely Neq, see Figure 1A) and disorder predicted values (Figure 1B,C) were not well spread. Hence, the correlation of Neq and Disopred3 was 0.37 (Figure 2B), and of Neq and PrDOS it was 0.34 (Figure 2C).
It is possible to divide Neq values into different clusters to have a better view of the prediction methods. Neq values of less than 4 correspond to the most rigid and the least flexible positions. Corresponding prediction values of Disopred3 and PrDOS were, respectively, 0.28 (Figure 1D) and 0.35 (Figure S1A). For intermediate Neq values (between 4 and 8, corresponding to flexible regions to the border of disorder [36]), average prediction values were 0.57 (Figure 1E) and 0.48 (Figure S1B), respectively. While for the disorder region (Neq higher than 8), these prediction values were 0.56 (Figure 1E) and 0.54 (Figure S1C), respectively.
These results showed clear and significant differences. Interestingly, both prediction methods displayed different distribution values, but often went to the same predictions and behaviors. For instance, in the disorder region (Neq higher than 8), their correlation was still excellent (0.76), as they both predicted high (disorder) and low (order) values (Figure S2).

3.3. General Tendencies

Previous analyses underlined the distribution of predicted values of Disopred3 and PrDOS, in regard to this new quantification. Figure 3 shows a similar computation, but these were done with the average values per class of Neq. Classes were designed for twelve values ranging from 1.0 to 12.0 (and higher). As often seen, the correlations became largely better using average values, i.e., the correlation is of 0.81 for Disopred3 (Figure 3A) and of 0.93 for PrDOS (Figure 3B).
These correlations looked good but did not reflect entirely the sensitivity of each method. Indeed, the excellent correlation of PrDOS came mainly from the limited variation of the predicted values (Figure 1C and Figure S3B) while Disopred3 was more pertinent.

4. Discussion and Conclusions

Intrinsically-disordered proteins and regions are complicated, as they do not have unique and simple characteristics. Hence, IDPs represent complete disordered proteins that stay disordered, but they can also adopt one conformation when they bind to their ligands or partners [66,67] or participate in multiple systems [68], they are essential to functions [69,70], drug design [71], and protein design [72].
For instance, NMR spectroscopy was used to delineate the sites of pre-structured motifs (PreSMos) [73]. PreSMos are transient local structural elements that presage target-bound conformations and act as specific determinants for IDP recognition by their target proteins [74]. Related to PreSMos are the famous molecular recognition features (MoRFs) that were identified in the x-ray structures of complexes [75] between target proteins and short fragments of IDPs/IDRs (predicted to be disordered) [76,77,78]. They were also linked to short linear motifs (SLiMs) that were found four times out of five in IDRs. The lengths of SLiMs range from 3 to 11 residues, and they have often been associated with pathologies, and characterized as structured when they interact with repetitive structures [79,80].
In previous studies, it was observed that local protein conformation deformation could be quantified and defined more properly in terms of rigidity and flexibility [15,62]. The analyses were extended to IDPs leading to a definition of an entropy scale ranging between 1 and 16, i.e., the number of PBs. An Neq of 1 corresponded to a rigid position while 8 was a disordered one, extending this categorization led to a Neq of 4 for a flexible region and of 6 for a highly flexible region. The analysis of IDPs also underlined a large number of IDRs and rigid regions [36]. Neq was a great tool to locate the mobile region encompassed in deformable (flexible) regions, and this was the same mechanism in IDPs. The question raised was then the reaction of disorder predictions on these data.
Intrinsic disorder predictors have been created from a wide variety of architectures and data sets with three main categories based on their underlying models: (a) ab initio methods based on the physiochemical characteristics, (b) machine-learning methods, such as PrDOS [55], and (c) meta methods, such as Disopred3 [53]. The relative performance of intrinsic disorder predictors has been compared many times [64,81] and we note the recent DISOselect analyses [82]. These all underlined the specificity of each approach, with two different methodologies were used here.
Firstly, Disopred3 is a complex approach to performing protein disorder prediction and protein-binding site annotation within disordered regions [53]. The tool first identifies disordered residues through a consensus of the output generated by Disopred2 [83] and two additional machine-learning-based modules trained on large IDRs. It then annotates them as protein binding through an additional support vector machine (SVM) classifier. Secondly, PrDOS [55] is composed of two predictors: (i) a predictor based on the local amino acid sequence, using a SVM algorithm for the position-specific score matrix, and (ii) one based on template proteins with the use of the conservation of intrinsic disorder in protein families using the Position specific iterative-Basic Local Alignment Search Tool (PSI-BLAST) approach [84].
As seen with Figure 1 and Figure 2, both approaches presented similar tendencies with a strong difference in the range of predicted values. The final correlations with Neq were limited. These two prediction methodologies were mainly controlled by the use of evolutionary information with effective neural networks. To go further, physics-based approaches were used, namely IUPred2A and ANCHOR2 [56]. Even if IUPred2A showed a distribution of prediction values close to the distribution of Disopred3 (Figure S6A), ANCHOR2 displayed a surprising binomial distribution with few values close to zero (Figure S6B). The correlations of IUPred2A and ANCHOR2 with Neq were particularly weak (0.29 and 0.25), leading to no particular improvements (Figure S6C,D). These approaches showed specificities, as (i) they had a correlation of 0.79 between them, but (ii) weak correlations with Disopred3 and PrDOS (between 0.65 and 0.44, see Table S1), underlying specific prediction patterns.
To go further, Neq was used to evaluate the quality of disorder prediction; the limit between order and disorder was defined by Neq (ranging between 1.0 and 12). Figure 4 summarizes the results with a limited success mainly between 35% and 42% (Table S2). These results do not mean that the prediction methods are of poor quality, but that a dedicated (and well-equilibrated) dataset must be used ([85]), with also well-balanced order and disorder state distribution. For instance, better prediction for Neq of 1 is due to a great imbalance for predicted order state. It is also a direct reflection of the fact that Neq is a particular measure and that we need the development of a specific prediction approach, such as OPAL+ which is specialized for MoRF prediction, to predict this type of feature [75].
As an interesting example, PED3 9AAC entry corresponded to alpha-synuclein. In its C-terminal part, both PrDOS and Disopred3 predicted disordered and highly disordered regions (orange and blue colors, respectively, on Figure 5A). The tendencies are similar with IUPred2A, ANCHOR2 [56], and the approaches proposed in DECIPHER [70]), while Neq was around 2 at these positions (red color on Figure 5A), i.e., a quite rigid region. Indeed, the visualization of the protein ensemble (Figure 5B) does not show any ordered regions, while PB distribution showed (Figure 5C, Figures S4 and S5) a large proportion of PB d around this region, i.e., a curved region (Figure 5D).
This type of example highlighted the interest in going further on a large dataset of IDPs and IDRs to present a better view of these cases. In the future, we would like to integrate different types of information to propose such methodologies that could be useful in different research areas. The PED3 database is an excellent source for analyses of both order and disorder states, with entirely disordered proteins and proteins with IDRs, i.e., mimicking a large spectrum of protein behaviors. Nonetheless, the number of data is still limited and it would be of great interest to add more information coming from other sources, computational and/or experimental.
In summary, analyses of IDPs in the light of structural alphabet underlined specific behaviors that were slightly different from classical IDPs/IDRs and the need to go further to find out if specific approaches and methodologies could be applied to it. It is therefore possible to define specific prediction methodologies that will separate mobile regions from pure disorder regions, i.e., rigid zones encompassed in highly-flexible deformable regions. It seems manageable, as we have seen that correlations with classical disorder predictions are not great (around 0.3, see Figure 2), but when average values are taken into account (Figure 3), correlations are clearly better (around 0.9).

Supplementary Materials

The following are available online at https://www.mdpi.com/2218-273X/10/7/1080/s1, Figure S1: Prediction disorder results of PrDOS on PED3 dataset. For Neq (A) lower than 4. (B) between 4 and 8 and (C) higher than 8. Figure S2: Prediction disorder results on PED3 dataset. (A) DisoPred3values (x-axis) against PrDOS values (y-axis) for Neq values higher than 8 (correlation is of 0.76). Figure S3: Analyses of prediction disorder results on PED3 dataset per class of Neq. (A) DisoPred3values (x-axis) and Neq classes (y-axis). (B) PrDOS values (x-axis) and Neq classes (y-axis). Figure S4: Neq values for the alpha-synuclein, a solution-state ensemble from PRE-NMR ensemble-restrained MD simulations (PED3 9AAC entry). Computation done with PBxplore software. Figure S5: PB distribution for the alpha-synuclein, a solution-state ensemble from PRE-NMR ensemble- restrained MD simulations (PED3 9AAC entry). Computation done with PBxplore software and represented with WebLogo. Figure S6: Distribution of Neq and prediction disorder values & Neq versus prediction disorder results. Distribution of (A) IUPred2A values (in purple), and (B) ANCHOR2 values (in pink), (C) Neq values (x-axis) against IUPred2A values (y-axis) (correlation equals to 0.29). (C) Neq values (x-axis) against ANCHOR2 values (y-axis) (correlation equals to 0.25). Table S1: Correlation between Neq, Disopred3, PrDOS, IUPRed2A and ANCHOR2 values on PED3 dataset. Table S2: Evaluation of prediction rate according to Neq values for Disopred3 approach.

Author Contributions

A.G.d.B. conceived, designed, and proposed the methodology, curated the data, performed the predictions, analyzed the results, wrote, reviewed, and edited the draft. The author has read and agreed to the published version of the manuscript.

Funding

This work was supported by grants from the Ministry of Research (France), University de Paris, University Paris Diderot, Sorbonne, Paris Cité (France), National Institute for Blood Transfusion (INTS, France), National Institute for Health and Medical Research (INSERM, France), IdEx ANR-18-IDEX-0001, and labex GR-Ex. The labex GR-Ex, reference ANR-11-LABX-0051 is funded by the program “Investissements d’avenir” of the French National Research Agency, reference ANR-11-IDEX-0005-02. AGdB acknowledges the French National Research Agency for grant ANR-19-CE17-0021 (BASIN) and the Indo-French Centre for the Promotion of Advanced Research/CEFIPRA for collaborative grant (number 5302-2). The author was granted access to high-performance computing (HPC) resources at the French National Computing Centre CINES under grants no. c2013037147, no. A0010707621, no. A0040710426, and no. A0070710961 funded by the GENCI (Grand Equipement National de Calcul Intensif). Calculations were also performed on an SGI cluster granted by Conseil Régional Ile de France and INTS (SESAME Grant). The APC was funded by National Institute for Health and Medical Research (INSERM, France).

Acknowledgments

A.G.d.B. thanks the reviewers who spent time evaluating this work and asked particularly relevant questions; their comments have greatly improved the manuscript. A.G.d.B. would also like to thank Nenad Mitic, Catherine Etchebest, his former students, Pierrick Craveur, Agnel Praveen Joseph, Tarun J. Narwani, Snoopy de Brevern, Nicolas K. Shinada, and Akhila Melarkode Vattekatte, and the organizers and participants of Belbi’2016 (Belgrade, Serbia), International Conference on IDP’2017 (IISER Mohali, Chandigarh, India) and Belbi’2018 (Belgrade, Serbia) for fruitful discussions.

Conflicts of Interest

The author declares no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Eisenberg, D. The discovery of the alpha-helix and beta-sheet, the principal structural features of proteins. Proc. Natl. Acad. Sci. USA 2003, 100, 11207–11210. [Google Scholar] [CrossRef] [Green Version]
  2. Unger, R.; Harel, D.; Wherland, S.; Sussman, J.L. A 3D building blocks approach to analyzing and predicting structure of proteins. Proteins 1989, 5, 355–373. [Google Scholar] [CrossRef]
  3. Offmann, B.; Tyagi, M.; de Brevern, A.G. Local Protein Structures. Curr. Bioinform. 2007, 3, 165–202. [Google Scholar] [CrossRef] [Green Version]
  4. Liu, X.; Zhao, Y.P.; Zheng, W.M. CLEMAPS: Multiple alignment of protein structures based on conformational letters. Proteins 2008, 71, 728–736. [Google Scholar] [CrossRef] [Green Version]
  5. Tung, C.H.; Huang, J.W.; Yang, J.M. Kappa-alpha plot derived structural alphabet and BLOSUM-like substitution matrix for rapid search of protein structure database. Genome Biol. 2007, 8, R31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Leonard, S.; Joseph, A.P.; Srinivasan, N.; Gelly, J.C.; de Brevern, A.G. mulPBA: An efficient multiple protein structure alignment method based on a structural alphabet. J. Biomol. Struct. Dyn. 2014, 32, 661–668. [Google Scholar] [CrossRef] [PubMed]
  7. Pandini, A.; Fornili, A.; Fraternali, F.; Kleinjung, J. GSATools: Analysis of allosteric communication and functional local motions using a structural alphabet. Bioinformatics 2013, 29, 2053–2055. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. Dudev, M.; Lim, C. Discovering structural motifs using a structural alphabet: Application to magnesium-binding sites. BMC Bioinform. 2007, 8, 106. [Google Scholar] [CrossRef] [Green Version]
  9. Narwani, T.J.; Etchebest, C.; Craveur, P.; Leonard, S.; Rebehmed, J.; Srinivasan, N.; Bornot, A.; Gelly, J.C.; de Brevern, A.G. In silico prediction of protein flexibility with local structure approach. Biochimie 2019, 165, 150–155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  10. Karchin, R.; Cline, M.; Mandel-Gutfreund, Y.; Karplus, K. Hidden Markov models that use predicted local structure for fold recognition: Alphabets of backbone geometry. Proteins 2003, 51, 504–514. [Google Scholar] [CrossRef]
  11. Ghouzam, Y.; Postic, G.; Guerin, P.E.; de Brevern, A.G.; Gelly, J.C. ORION: A web server for protein fold recognition and structure prediction using evolutionary hybrid profiles. Sci. Rep. 2016, 6, 28268. [Google Scholar] [CrossRef] [PubMed]
  12. de Brevern, A.G.; Etchebest, C.; Hazout, S. Bayesian probabilistic approach for predicting backbone structures in terms of protein blocks. Proteins 2000, 41, 271–287. [Google Scholar] [CrossRef] [Green Version]
  13. Craveur, P.; Joseph, A.P.; Esque, J.; Narwani, T.J.; Noel, F.; Shinada, N.; Goguet, M.; Leonard, S.; Poulain, P.; Bertrand, O.; et al. Protein flexibility in the light of structural alphabets. Front. Mol. Biosci. 2015, 2, 20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Craveur, P.; Narwani, T.J.; Rebehmed, J.; de Brevern, A.G. Investigation of the impact of PTMs on the protein backbone conformation. Amino Acids 2019, 51, 1065–1079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  15. Narwani, T.J.; Craveur, P.; Shinada, N.K.; Floch, A.; Santuz, H.; Vattekatte, A.M.; Srinivasan, N.; Rebehmed, J.; Gelly, J.C.; Etchebest, C.; et al. Discrete analyses of protein dynamics. J. Biomol. Struct. Dyn. 2019, 1–15. [Google Scholar] [CrossRef] [PubMed]
  16. Goguet, M.; Narwani, T.J.; Petermann, R.; Jallu, V.; de Brevern, A.G. In silico analysis of Glanzmann variants of Calf-1 domain of alphaIIbbeta3 integrin revealed dynamic allosteric effect. Sci. Rep. 2017, 7, 8001. [Google Scholar] [CrossRef] [Green Version]
  17. Craveur, P.; Gres, A.T.; Kirby, K.A.; Liu, D.; Hammond, J.A.; Deng, Y.; Forli, S.; Goodsell, D.S.; Williamson, J.R.; Sarafianos, S.G.; et al. Novel Intersubunit Interaction Critical for HIV-1 Core Assembly Defines a Potentially Targetable Inhibitor Binding Pocket. mBio 2019, 10, e02858-18. [Google Scholar] [CrossRef] [Green Version]
  18. Ladislav, M.; Cerny, J.; Krusek, J.; Horak, M.; Balik, A.; Vyklicky, L. The LILI Motif of M3-S2 Linkers Is a Component of the NMDA Receptor Channel Gate. Front. Mol. Neurosci. 2018, 11, 113. [Google Scholar] [CrossRef] [Green Version]
  19. van der Lee, R.; Buljan, M.; Lang, B.; Weatheritt, R.J.; Daughdrill, G.W.; Dunker, A.K.; Fuxreiter, M.; Gough, J.; Gsponer, J.; Jones, D.T.; et al. Classification of intrinsically disordered regions and proteins. Chem. Rev. 2014, 114, 6589–6631. [Google Scholar] [CrossRef]
  20. Peng, Z.; Yan, J.; Fan, X.; Mizianty, M.J.; Xue, B.; Wang, K.; Hu, G.; Uversky, V.N.; Kurgan, L. Exceptionally abundant exceptions: Comprehensive characterization of intrinsic disorder in all domains of life. Cell. Mol. Life Sci. 2015, 72, 137–151. [Google Scholar] [CrossRef]
  21. Habchi, J.; Tompa, P.; Longhi, S.; Uversky, V.N. Introducing protein intrinsic disorder. Chem. Rev. 2014, 114, 6561–6588. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Wright, P.E.; Dyson, H.J. Intrinsically unstructured proteins: Re-assessing the protein structure-function paradigm. J. Mol. Biol. 1999, 293, 321–331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Uversky, V.N. Cracking the folding code. Why do some proteins adopt partially folded conformations, whereas other don’t? FEBS Lett. 2002, 514, 181–183. [Google Scholar] [CrossRef]
  24. Mitic, N.S.; Malkov, S.N.; Kovacevic, J.J.; Pavlovic-Lazetic, G.M.; Beljanski, M.V. Structural disorder of plasmid-encoded proteins in Bacteria and Archaea. BMC Bioinform. 2018, 19, 158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  25. Toto, A.; Malagrino, F.; Visconti, L.; Troilo, F.; Pagano, L.; Brunori, M.; Jemth, P.; Gianni, S. Templated folding of intrinsically disordered proteins. J. Biol. Chem. 2020, 295, 6586–6593. [Google Scholar] [CrossRef] [Green Version]
  26. Tompa, P. Intrinsically unstructured proteins. Trends Biochem. Sci. 2002, 27, 527–533. [Google Scholar] [CrossRef]
  27. Dunker, A.K.; Lawson, J.D.; Brown, C.J.; Williams, R.M.; Romero, P.; Oh, J.S.; Oldfield, C.J.; Campen, A.M.; Ratliff, C.M.; Hipps, K.W.; et al. Intrinsically disordered protein. J. Mol. Graph. Model. 2001, 19, 26–59. [Google Scholar] [CrossRef] [Green Version]
  28. Kragelj, J.; Blackledge, M.; Jensen, M.R. Ensemble Calculation for Intrinsically Disordered Proteins Using NMR Parameters. Adv. Exp. Med. Biol. 2015, 870, 123–147. [Google Scholar]
  29. Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [Green Version]
  30. Ezerski, J.C.; Zhang, P.; Jennings, N.C.; Waxham, M.N.; Cheung, M.S. Molecular Dynamics Ensemble Refinement of Intrinsically Disordered Peptides According to Deconvoluted Spectra from Circular Dichroism. Biophys. J. 2020, 118, 1665–1678. [Google Scholar] [CrossRef]
  31. Chen, J.; Liu, X.; Chen, J. Targeting Intrinsically Disordered Proteins through Dynamic Interactions. Biomolecules 2020, 10, 743. [Google Scholar] [CrossRef] [PubMed]
  32. Thorpe, M.F.; Lei, M.; Rader, A.J.; Jacobs, D.J.; Kuhn, L.A. Protein flexibility and dynamics using constraint theory. J. Mol. Graph. Model. 2001, 19, 60–69. [Google Scholar] [CrossRef] [Green Version]
  33. Carugo, O. Atomic displacement parameters in structural biology. Amino Acids 2018, 50, 775–786. [Google Scholar] [CrossRef] [PubMed]
  34. Uversky, V.N. Intrinsic disorder here, there, and everywhere, and nowhere to escape from it. Cell. Mol. Life Sci. 2017, 74, 3065–3067. [Google Scholar] [CrossRef]
  35. Varadi, M.; Kosol, S.; Lebrun, P.; Valentini, E.; Blackledge, M.; Dunker, A.K.; Felli, I.C.; Forman-Kay, J.D.; Kriwacki, R.W.; Pierattelli, R.; et al. pE-DB: A database of structural ensembles of intrinsically disordered and of unfolded proteins. Nucleic Acids Res. 2014, 42, D326–D335. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  36. Melarkode Vattekatte, A.; Narwani, T.J.; Floch, A.; Maljkovic, M.; Bisoo, S.; Shinada, N.K.; Kranjc, A.; Gelly, J.C.; Srinivasan, N.; Mitic, N.; et al. A structural entropy index to analyse local conformations in intrinsically disordered proteins. J. Struct. Biol. 2020, 210, 107464. [Google Scholar]
  37. Melarkode Vattekatte, A.; Narwani, T.J.; Floch, A.; Maljkovic, M.; Bisoo, S.; Shinada, N.K.; Kranjc, A.; Gelly, J.C.; Srinivasan, N.; Mitic, N.; et al. Data set of intrinsically disordered proteins analysed at a local protein conformation level. Data Brief 2020, 29, 105383. [Google Scholar] [CrossRef]
  38. Mittag, T.; Marsh, J.; Grishaev, A.; Orlicky, S.; Lin, H.; Sicheri, F.; Tyers, M.; Forman-Kay, J.D. Structure/function implications in a dynamic complex of the intrinsically disordered Sic1 with the Cdc4 subunit of an SCF ubiquitin ligase. Structure 2010, 18, 494–506. [Google Scholar] [CrossRef] [Green Version]
  39. Weeks, S.D.; Baranova, E.V.; Heirbaut, M.; Beelen, S.; Shkumatov, A.V.; Gusev, N.B.; Strelkov, S.V. Molecular structure and dynamics of the dimeric human small heat shock protein HSPB6. J. Struct. Biol. 2014, 185, 342–354. [Google Scholar] [CrossRef]
  40. Allison, J.R.; Rivers, R.C.; Christodoulou, J.C.; Vendruscolo, M.; Dobson, C.M. A relationship between the transient structure in the monomeric state and the aggregation propensities of alpha-synuclein and beta-synuclein. Biochemistry 2014, 53, 7170–7183. [Google Scholar] [CrossRef]
  41. Sivakolundu, S.G.; Bashford, D.; Kriwacki, R.W. Disordered p27Kip1 exhibits intrinsic structure resembling the Cdk2/cyclin A-bound conformation. J. Mol. Biol. 2005, 353, 1118–1128. [Google Scholar] [CrossRef] [PubMed]
  42. Mertens, H.D.; Piljic, A.; Schultz, C.; Svergun, D.I. Conformational analysis of a genetically encoded FRET biosensor by SAXS. Biophys. J. 2012, 102, 2866–2875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Bacot-Davis, V.R.; Ciomperlik, J.J.; Basta, H.A.; Cornilescu, C.C.; Palmenberg, A.C. Solution structures of Mengovirus Leader protein, its phosphorylated derivatives, and in complex with nuclear transport regulatory protein, RanGTPase. Proc. Natl. Acad. Sci. USA 2014, 111, 15792–15797. [Google Scholar] [CrossRef] [Green Version]
  44. Sanchez-Martinez, M.; Crehuet, R. Application of the maximum entropy principle to determine ensembles of intrinsically disordered proteins from residual dipolar couplings. Phys. Chem. Chem. Phys. 2014, 16, 26030–26039. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  45. Sterckx, Y.G.; Volkov, A.N.; Vranken, W.F.; Kragelj, J.; Jensen, M.R.; Buts, L.; Garcia-Pino, A.; Jove, T.; Van Melderen, L.; Blackledge, M.; et al. Small-angle X-ray scattering- and nuclear magnetic resonance-derived conformational ensemble of the highly flexible antitoxin PaaA2. Structure 2014, 22, 854–865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  46. De Biasio, A.; Ibanez de Opakua, A.; Cordeiro, T.N.; Villate, M.; Merino, N.; Sibille, N.; Lelli, M.; Diercks, T.; Bernado, P.; Blanco, F.J. p15PAF is an intrinsically disordered protein with nonrandom structural preferences at sites of interaction with other proteins. Biophys. J. 2014, 106, 865–874. [Google Scholar] [CrossRef] [Green Version]
  47. Ozenne, V.; Schneider, R.; Yao, M.; Huang, J.R.; Salmon, L.; Zweckstetter, M.; Jensen, M.R.; Blackledge, M. Mapping the potential energy landscape of intrinsically disordered proteins at amino acid resolution. J. Am. Chem. Soc. 2012, 134, 15138–15148. [Google Scholar] [CrossRef] [Green Version]
  48. Marsh, J.A.; Forman-Kay, J.D. Structure and disorder in an unfolded state under nondenaturing conditions from ensemble models consistent with a large number of experimental restraints. J. Mol. Biol. 2009, 391, 359–374. [Google Scholar] [CrossRef]
  49. Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
  50. Joseph, A.P.; Agarwal, G.; Mahajan, S.; Gelly, J.-C.; Swapna, L.S.; Offmann, B.; Cadet, F.; Bornot, A.; Tyagi, M.; Valadié, H.; et al. A short survey on Protein Blocks. Biophys. Rev. 2010, 2, 137–145. [Google Scholar] [CrossRef]
  51. Jallu, V.; Poulain, P.; Fuchs, P.F.; Kaplan, C.; de Brevern, A.G. Modeling and molecular dynamics simulations of the V33 variant of the integrin subunit beta3: Structural comparison with the L33 (HPA-1a) and P33 (HPA-1b) variants. Biochimie 2014, 105, 84–90. [Google Scholar] [CrossRef] [PubMed]
  52. Barnoud, J.; Santuz, H.; Craveur, P.; Joseph, A.P.; Jallu, V.; de Brevern, A.G.; Poulain, P. PBxplore: A tool to analyze local protein structure and deformability with Protein Blocks. PeerJ 2017, 5, e4013. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Jones, D.T.; Cozzetto, D. DISOPRED3: Precise disordered region predictions with annotated protein-binding activity. Bioinformatics 2015, 31, 857–863. [Google Scholar] [CrossRef]
  54. Buchan, D.W.A.; Jones, D.T. The PSIPRED Protein Analysis Workbench: 20 years on. Nucleic Acids Res. 2019, 47, W402–W407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  55. Ishida, T.; Kinoshita, K. PrDOS: Prediction of disordered protein regions from amino acid sequence. Nucleic Acids Res. 2007, 35, W460–W464. [Google Scholar] [CrossRef] [PubMed]
  56. Meszaros, B.; Erdos, G.; Dosztanyi, Z. IUPred2A: Context-dependent prediction of protein disorder as a function of redox state and protein binding. Nucleic Acids Res. 2018, 46, W329–W337. [Google Scholar] [CrossRef] [PubMed]
  57. Erdos, G.; Dosztanyi, Z. Analyzing Protein Disorder with IUPred2A. Curr. Protoc. Bioinform. 2020, 70, e99. [Google Scholar] [CrossRef] [Green Version]
  58. Python Software Foundation. Available online: https://www.python.org/ (accessed on 14 June 2020).
  59. R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. 2017. Available online: https://www.R-project.org/ (accessed on 14 June 2020).
  60. Schrodinger, LLC. The PyMOL Molecular Graphics System, Version 1.7.2.2; Schrodinger, LLC: New York, NY, USA, 2015. [Google Scholar]
  61. DeLano, W.L.T. The PyMOL Molecular Graphics System; DeLano Scientific: San Carlos, CA, USA, 2002. Available online: http://www.pymol.org (accessed on 14 June 2020).
  62. Narwani, T.J.; Craveur, P.; Shinada, N.K.; Santuz, H.; Rebehmed, J.; Etchebest, C.; de Brevern, A.G. Dynamics and deformability of α-, 310- and π-helices. Arch. Biol. Sci. 2018, 70, 21–31. [Google Scholar] [CrossRef]
  63. Pavlovic-Lazetic, G.M.; Mitic, N.S.; Kovacevic, J.J.; Obradovic, Z.; Malkov, S.N.; Beljanski, M.V. Bioinformatics analysis of disordered proteins in prokaryotes. BMC Bioinform. 2011, 12, 66. [Google Scholar] [CrossRef] [Green Version]
  64. Nielsen, J.T.; Mulder, F.A.A. Quality and bias of protein disorder predictors. Sci. Rep. 2019, 9, 5137. [Google Scholar] [CrossRef] [Green Version]
  65. de Brevern, A.G.; Bornot, A.; Craveur, P.; Etchebest, C.; Gelly, J.C. PredyFlexy: Flexibility and local structure prediction from sequence. Nucleic Acids Res. 2012, 40, W317–W322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  66. Perdigao, N.; Rosa, A. Dark Proteome Database: Studies on Dark Proteins. High Throughput 2019, 8, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  67. Lieutaud, P.; Ferron, F.; Uversky, A.V.; Kurgan, L.; Uversky, V.N.; Longhi, S. How disordered is my protein and what is its disorder for? A guide through the “dark side” of the protein universe. Intrinsically Disord Proteins 2016, 4, e1259708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  68. Uversky, V.N.; Finkelstein, A.V. Life in Phases: Intra- and Inter- Molecular Phase Transitions in Protein Solutions. Biomolecules 2019, 9, 842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  69. Uversky, V.N. New technologies to analyse protein function: An intrinsic disorder perspective. F1000Res 2020, 9, F1000 Faculty Rev-101. [Google Scholar] [CrossRef] [Green Version]
  70. Barik, A.; Katuwawala, A.; Hanson, J.; Paliwal, K.; Zhou, Y.; Kurgan, L. DEPICTER: Intrinsic Disorder and Disorder Function Prediction Server. J. Mol. Biol 2020, 432, 3379–3387. [Google Scholar] [CrossRef]
  71. Blundell, T.L.; Gupta, M.N.; Hasnain, S.E. Intrinsic disorder in proteins: Relevance to protein assemblies, drug design and host-pathogen interactions. Prog. Biophys. Mol. Biol. 2020. [Google Scholar] [CrossRef]
  72. Nagibina, G.S.; Glukhova, K.A.; Uversky, V.N.; Melnik, T.N.; Melnik, B.S. Intrinsic Disorder-Based Design of Stable Globular Proteins. Biomolecules 2019, 10, 64. [Google Scholar] [CrossRef] [Green Version]
  73. Lee, S.H.; Kim, D.H.; Han, J.J.; Cha, E.J.; Lim, J.E.; Cho, Y.J.; Lee, C.; Han, K.H. Understanding pre-structured motifs (PreSMos) in intrinsically unfolded proteins. Curr. Protein Pept. Sci. 2012, 13, 34–54. [Google Scholar] [CrossRef]
  74. Kim, D.H.; Han, K.H. PreSMo Target-Binding Signatures in Intrinsically Disordered Proteins. Mol. Cells 2018, 41, 889–899. [Google Scholar]
  75. Sharma, R.; Sharma, A.; Raicar, G.; Tsunoda, T.; Patil, A. OPAL+: Length-Specific MoRF Prediction in Intrinsically Disordered Protein Sequences. Proteomics 2019, 19, e1800058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  76. Mohan, A.; Oldfield, C.J.; Radivojac, P.; Vacic, V.; Cortese, M.S.; Dunker, A.K.; Uversky, V.N. Analysis of molecular recognition features (MoRFs). J. Mol. Biol. 2006, 362, 1043–1059. [Google Scholar] [CrossRef]
  77. Vacic, V.; Oldfield, C.J.; Mohan, A.; Radivojac, P.; Cortese, M.S.; Uversky, V.N.; Dunker, A.K. Characterization of molecular recognition features, MoRFs, and their binding partners. J. Proteome Res. 2007, 6, 2351–2366. [Google Scholar] [CrossRef] [Green Version]
  78. Oldfield, C.J.; Cheng, Y.; Cortese, M.S.; Romero, P.; Uversky, V.N.; Dunker, A.K. Coupled folding and binding with alpha-helix-forming molecular recognition elements. Biochemistry 2005, 44, 12454–12470. [Google Scholar] [CrossRef] [PubMed]
  79. Ren, S.; Uversky, V.N.; Chen, Z.; Dunker, A.K.; Obradovic, Z. Short Linear Motifs recognized by SH2, SH3 and Ser/Thr Kinase domains are conserved in disordered protein regions. BMC Genom. 2008, 9 (Suppl. 2), S26. [Google Scholar] [CrossRef] [Green Version]
  80. Van Roey, K.; Uyar, B.; Weatheritt, R.J.; Dinkel, H.; Seiler, M.; Budd, A.; Gibson, T.J.; Davey, N.E. Short linear motifs: Ubiquitous and functionally diverse protein interaction modules directing cell regulation. Chem. Rev. 2014, 114, 6733–6778. [Google Scholar] [CrossRef] [PubMed]
  81. Hu, G.; Wu, Z.; Oldfield, C.J.; Wang, C.; Kurgan, L. Quality assessment for the putative intrinsic disorder in proteins. Bioinformatics 2019, 35, 1692–1700. [Google Scholar] [CrossRef] [Green Version]
  82. Katuwawala, A.; Oldfield, C.J.; Kurgan, L. DISOselect: Disorder predictor selection at the protein level. Protein Sci. 2020, 29, 184–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  83. Ward, J.J.; Sodhi, J.S.; McGuffin, L.J.; Buxton, B.F.; Jones, D.T. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J. Mol. Biol. 2004, 337, 635–645. [Google Scholar] [CrossRef]
  84. Altschul, S.F.; Madden, T.L.; Schaffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [Green Version]
  85. Vincent, M.; Uversky, V.N.; Schnell, S. On the Need to Develop Guidelines for Characterizing and Reporting Intrinsic Disorder in Proteins. Proteomics 2019, 19, e1800415. [Google Scholar] [CrossRef] [PubMed]
  86. Crooks, G.E.; Hon, G.; Chandonia, J.M.; Brenner, S.E. WebLogo: A sequence logo generator. Genome Res. 2004, 14, 1188–1190. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Biomolecules 10 01080 g001 550
Figure 1. Distribution of an equivalent number of PBs (Neq) and prediction disorder values. (A) Neq values (in red), (B) Disopred3 values (in orange), (C) PrDOS values (in green), (D) Disopred3 values for Neq values lower than 4, (E) Disopred3 values for Neq values between 4 and 8, and (F) Disopred3 values for Neq values higher than 8.
Figure 1. Distribution of an equivalent number of PBs (Neq) and prediction disorder values. (A) Neq values (in red), (B) Disopred3 values (in orange), (C) PrDOS values (in green), (D) Disopred3 values for Neq values lower than 4, (E) Disopred3 values for Neq values between 4 and 8, and (F) Disopred3 values for Neq values higher than 8.
Biomolecules 10 01080 g001
Biomolecules 10 01080 g002 550
Figure 2. Neq versus prediction disorder results. (A) Disopred3 values (x-axis) against PrDOS values (y-axis) (correlation equals to 0.75), (B) Neq values (x-axis) against Disopred3 values (y-axis) (correlation equals to 0.37) and (C) Neq values (x-axis) against PrDOS values (y-axis) (correlation equals to 0.34).
Figure 2. Neq versus prediction disorder results. (A) Disopred3 values (x-axis) against PrDOS values (y-axis) (correlation equals to 0.75), (B) Neq values (x-axis) against Disopred3 values (y-axis) (correlation equals to 0.37) and (C) Neq values (x-axis) against PrDOS values (y-axis) (correlation equals to 0.34).
Biomolecules 10 01080 g002
Biomolecules 10 01080 g003 550
Figure 3. Analyses of Neq versus prediction disorder results on PED3 dataset. (A) Neq values (x-axis) vs. average Disopred3 values (y-axis) (correlation is of 0.81) and (B) Neq values (X-axis) vs. average PrDOS values (y-axis) (correlation is of 0.93).
Figure 3. Analyses of Neq versus prediction disorder results on PED3 dataset. (A) Neq values (x-axis) vs. average Disopred3 values (y-axis) (correlation is of 0.81) and (B) Neq values (X-axis) vs. average PrDOS values (y-axis) (correlation is of 0.93).
Biomolecules 10 01080 g003
Biomolecules 10 01080 g004 550
Figure 4. Evaluation of Disopred3 predictions at the light of Neq values. Neq values ranging from 1.0 to 12 are provided with the prediction rate (in red). The contribution of disordered and ordered positions are defined by the Neq values.
Figure 4. Evaluation of Disopred3 predictions at the light of Neq values. Neq values ranging from 1.0 to 12 are provided with the prediction rate (in red). The contribution of disordered and ordered positions are defined by the Neq values.
Biomolecules 10 01080 g004
Biomolecules 10 01080 g005 550
Figure 5. Example of alpha-synuclein, a solution-state ensemble from paramagnetic relaxation enhancement-Nuclear magnetic resonance (PRE-NMR) ensemble-restrained MD simulations (PED3 9AAC entry). (A) A zoom on C-terminus of alpha-synuclein was done. Along the x-axis are shown, in orange, PrDOS prediction values and, in blue, Disopred3values. Neq values are represented in red. (B) A superimposition of hundreds of structural models from the ensemble. (C) Representation in terms of PBs shown with WebLogo [86], underlying the most contradictory position (low Neq and high disorder prediction values). (D) A dozen structural models superimposed on this region.
Figure 5. Example of alpha-synuclein, a solution-state ensemble from paramagnetic relaxation enhancement-Nuclear magnetic resonance (PRE-NMR) ensemble-restrained MD simulations (PED3 9AAC entry). (A) A zoom on C-terminus of alpha-synuclein was done. Along the x-axis are shown, in orange, PrDOS prediction values and, in blue, Disopred3values. Neq values are represented in red. (B) A superimposition of hundreds of structural models from the ensemble. (C) Representation in terms of PBs shown with WebLogo [86], underlying the most contradictory position (low Neq and high disorder prediction values). (D) A dozen structural models superimposed on this region.
Biomolecules 10 01080 g005

Share and Cite

MDPI and ACS Style

de Brevern, A.G. Analysis of Protein Disorder Predictions in the Light of a Protein Structural Alphabet. Biomolecules 2020, 10, 1080. https://doi.org/10.3390/biom10071080

AMA Style

de Brevern AG. Analysis of Protein Disorder Predictions in the Light of a Protein Structural Alphabet. Biomolecules. 2020; 10(7):1080. https://doi.org/10.3390/biom10071080

Chicago/Turabian Style

de Brevern, Alexandre G. 2020. "Analysis of Protein Disorder Predictions in the Light of a Protein Structural Alphabet" Biomolecules 10, no. 7: 1080. https://doi.org/10.3390/biom10071080

APA Style

de Brevern, A. G. (2020). Analysis of Protein Disorder Predictions in the Light of a Protein Structural Alphabet. Biomolecules, 10(7), 1080. https://doi.org/10.3390/biom10071080

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop