Line-Constrained Shape Feature for Building Change Detection in VHR Remote Sensing Imagery

Abstract

Buildings represent the most relevant features of human activity in urban regions, but their change detection using very-high-resolution (VHR) remote sensing imagery is still a major challenge. Effective representation of the building is the key point in building change detection. The linear feature can indirectly represent the structure and distribution of man-made objects. Thus, this study proposes a shape feature-based building change detection method. Specifically, a line-constrained shape (LCS) feature is developed to capture the shape characteristics of buildings. This feature improves the discriminability between buildings and other ground objects by integrating the pixel shape feature and line segments. The building candidate area (BCA) is created in accordance with the distribution of the line segments in two-phase images. The problem space is constrained in a high-likelihood region of buildings because of the BCA. Comparative experimental results demonstrate that the combination of the spectral feature and the developed LCS feature achieves the best performance in object-based building change detection in VHR imagery.

1. Introduction

The development of human society is always accompanied by people’s frequent interactions with nature. Among the environmental changes, land use/cover changes in urban areas appear more frequent and complex. Obtaining change information in time is crucial for the government to make decisions on urban construction, planning and management [1,2,3,4]. Singh [5] defined change detection as “the process of identifying differences in the state of an object or phenomenon by observing it at different times”. Multitemporal remote sensing images have become a major data source for change detection due to the high temporal frequency, digital format suitable for computation, synoptic view, and wide selection of spatial and spectral resolutions [6,7], while tradeoff should be considered when applying the temporal, spatial and spectral resolutions depending on the satellite or sensor. Meanwhile, a large number of change detection methods have been widely developed over the past decades [8,9].

The traditional change detection methods use medium- and low-spatial-resolution remote sensing images as data sources but are mostly pixel based, where the pixel is the basic analysis unit. Spectral features are normally used to detect and measure changes, but spatial characteristics are generally not considered [3]. The pixel feature comparison-based change detection has the advantages of fast calculation speed and easy-to-understand results, but it is susceptible to the influences of geometric registration and radiation correction errors between different temporal data [10]. Many works in the literature have reviewed the methods of pixel-based change detection [4,11,12]. With the increase in spatial resolution, the information contained in remote sensing images becomes abundant, which provides a rich basis to support change detection. However, in VHR remote sensing images, the complex spatial distribution of objects and large heterogeneity usually occur between individual objects. They lead to a great challenge in the change detection task. Facing the phenomenon of “high intraclass variability and low interclass variability”, a traditional pixel-based change detection method is not suitable for VHR image processing [3,9].

The object-based image analysis (OBIA) method shows an obvious advantage over the pixel-based method. In recent years, the OBIA approach has been proven to have a considerable advantage in the change detection field, and it is continuously developing [1,13,14]. The image object is the basic analysis unit of object-based change detection (OBCD). The image is divided into several meaningful homogeneous regions, that is, the image objects [15,16]. Each object consists of a set of pixels that are spatially adjacent and similar in feature (e.g., spectra) [17], thereby allowing the change detection to use the spatial information efficiently [1]. Many OBCD approaches have been established. For instance, a fast OBCD method was proposed in [18]. In the method, two-phase images were segmented and overlapped to obtain synthesized objects. For every object, the spectral characteristic and change vector (CV) value were extracted. On the basis of these features, the transductive SVM was used to classify the changed and unchanged objects.

In urban areas, buildings are the most relevant features of human activities and an important manifestation of urbanization. Accurate change detection of buildings is vital in promoting urban planning and achieving sustainable development of the environment [19]. As for the buildings in VHR remote sensing images, their structures are different and their colors are diverse; the spectral characteristics of some buildings may also be confused with those of some non-buildings. Spectral characteristics are ineffective in distinguishing changed buildings [20,21]; therefore, other means are introduced to overcome the deficiency, among which spatial analysis is a widely accepted means [22].

Numerous man-made objects (e.g., buildings) in urban areas have rich corner points and regular appearance shapes. Establishing the spatial feature that contains the shape information of buildings can be convenient for building extraction and change detection in VHR images. For example, feature points and line information are obtained to get buildings’ locations [23,24,25]; indexes that can describe specific attributes of buildings are designed, such as the length and width of connected pixel groups [26], the pixel shape index (PSI) [27] and the morphological building index (MBI) [28]; and a deep convolutional neural network is used to find the expression of the characteristics of buildings [29,30,31]. By combining spatial features and shape information with spectrum and texture features, various methods have been proposed for building extraction and change detection [23,24,25,26,27,28,29,30,31,32,33,34,35,36].

However, the diversity of buildings in VHR remote sensing images is various, that is, differences in spectral, shape, textural and spatial background information naturally exist among buildings. A specific template for accurately depicting the shape and boundary of buildings is difficult to construct even in a certain area. For example, the spectral threshold used to stop the extension vector in PSI is likely to confuse some buildings with their surrounding objects (e.g., bare, grassland or shadow) because of the similar spectral appearance. MBI depends on the luminance image defined as the maximum value of all bands, and it easily ignores the brightness difference of buildings and overlooks some buildings with low brightness. Therefore, encoding the crucial characteristic of buildings in VHR images is a key issue in building change detection research.

A large number of line segments can be extracted from the outer appearance of buildings in VHR images. Consequently, a clustering of line features will emerge in the area where buildings are located. From this viewpoint, lines should be taken as the inherent characteristics to grasp building shapes. In this paper, we present a line-constrained shape (LCS) feature, which more easily distinguishes buildings from other geo-objects. Based on LCS and a spectral feature, an object-based supervised classification method is proposed for building change detection in VHR remote sensing imagery.

The rest of the paper is organized as follows. Section 2 elucidates the proposed method. Section 3 provides the experimental result analysis and the comparison of building change detection based on different spatial features. Section 4 elaborates the conclusion and the future work. The acronyms used in this study are summarized in the Abbreviation section.

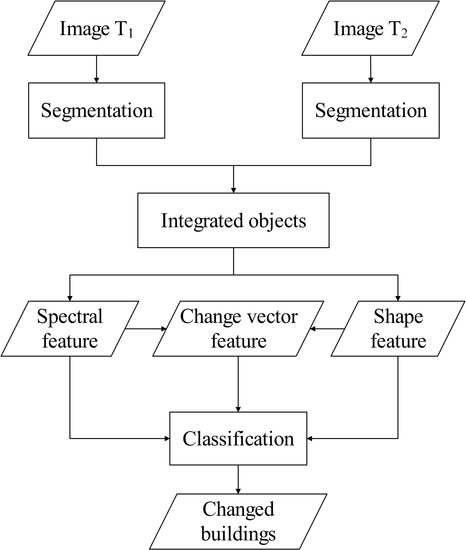
2. Methodology

The LCS-based building change detection method proposed in this study mainly contains three steps. First, two-phase images are segmented, and basic analysis units are created by synthesizing the corresponding two-phase objects. Then, line segments are extracted in VHR remote sensing images, and the LCS is accordingly developed to represent the shape feature. Finally, a feature vector that connects spectral, shape and differential information is built for each of the basic analysis units, and it is input to an object-based supervised classification to obtain changed buildings. The flowchart of the proposed method is shown in Figure 1.

2.1. Image Object Generation

By performing OBIA, we can utilize the rich information in VHR remote sensing imagery. The image is firstly segmented into objects, then feature extraction is implemented on the object level, and object-based classification is applied to obtain the final result. The segmentation method, as the front-end step and key part in OBIA, and its output will greatly affect the results of subsequent steps [37]. Here, the simple linear iterative clustering (SLIC) [38] is adopted considering that it can produce compact and homogeneous objects and is excellent in performance speed, contour preserving and shape characterization. Therefore, the SLIC is utilized to segment two-phase images into image objects for achieving object homogeneity. Finally, an object synthesis method [18] is adopted to acquire the final analysis units.

2.2. Shape Feature Extraction

This study focuses on the shape features of buildings to enhance the representing ability of features in building change detection. The calculation of the shape features is constrained by straight lines by utilizing the shape and position information of buildings. The likelihood of pixels belonging to buildings is calculated on the basis of line segments, and the BCA is extracted in accordance with the likelihood. A special assignment strategy is proposed to embody the LCS difference between the objects in BCA and outside objects.

2.2.1. Building Likelihood Map

Although spectra and structural diversity generally represent buildings, the lines of buildings are obvious in VHR images. Large numbers of line segments can be extracted from the extrinsic structure and contour of buildings. The proposed method uses a line segment detector (LSD) [39] to extract the line segments from two-phase images. The LSD can obtain subpixel accuracy, and its result includes the coordinate of the endpoints, width, and orientation of segments. As shown in Figure 2a, the line segments of buildings and non-buildings exhibit differences, namely, the irregular shape of the non-building objects produces random, sporadic and sparse line segments; the line segments can be more densely extracted in the building area. These lines can express the position and shape information of buildings to a large extent.

Figure 2a illustrates that, if numerous line segments exist around a pixel, then the likelihood belonging to the building of this pixel is high. In accordance with this characteristic, this study calculates the likelihood by using Gauss function. A building likelihood (BL) map is created depending on the Gauss function’s attribute by the rule that the decrease in the correlation of two pixels is accompanied with the increase in their spatial distance. The BL is calculated as

$$\mathrm{BL}(x,y)={\displaystyle \sum _{j=1}^{N_p}{e}^{-\frac{{(x-x_j)}^2+{(y-y_j)}^2}{2{\omega }^2}}},$$

(1)

where (x, y) is the coordinate of the current center pixel; ($x_j$,$y_j$) is the coordinate of the J_th pixel on line segment (POL); $N_p$ is the total number of all extracted POLs; ω is the scale factor of each POL’s influence range; and BL(x, y) is the total BL value of the center pixel (x, y). The POLs are collected from every one line segment with an interval of five pixels in consideration of computational efficiency. These discrete points can retain their representation of buildings’ location and shape information.

Equation (1) implies that a high ω indicates a large influence of range R and a high BL value for the center pixel. If the distance from POL to the center pixel is largely beyond the range R, then the BL value of the pixel will become too small to be ignored. As a result, the nearer the pixels are from POLs, the higher their BL values are, and vice versa.

The BL value of a center pixel is the accumulation of POLs’ influence; therefore, BL can be considered a measure of POL spatial distribution. When the center pixel is surrounded by POLs, the likelihood that the center pixel belongs to the building is high. Figure 2b is a BL map of an image block of buildings, which has been normalized into 0–1. The regions with warm color indicate a high likelihood value. The BL values of buildings are higher than those of the surrounding objects.

2.2.2. Building Candidate Area

Otsu [40] is used to extract the initial BCA from the BL map. Figure 2c shows the initial BCA, which is embraced by the smooth outline of the blue region. In this area, blue denotes the pixels that belong to other objects, and green stands for the building pixels. As shown in Figure 2c, parts of buildings (red region) are excluded from the BCA.

The objects are synthesized by bi-temporal objects as mentioned in Section 2.1. Consequently, as shown in Figure 2c, the area of these objects is small with very high internal homogeneity and an edge that can efficiently capture the actual edge of ground objects. A procedure for optimizing the candidate area is proposed to make the edge of the candidate area fit for the actual ground objects’ edges. Specifically, the candidate area is overlapped with all objects to extend the BCA. If any pixels (even only one) of an object locate in the BCA, then all pixels of the object are incorporated into the BCA. After all objects have experienced the procedure, the final extended BCA can be obtained, as shown in Figure 2d. The objects are small, and their internal homogeneity is high. The extended candidate area cannot greatly change the range of initial BCA. Furthermore, the extended region of the BCA will not introduce any other ground objects due to the high internal homogeneity of these objects.

2.2.3. Line-Constrained Shape Feature

The original PSI [27] takes the center pixel as the starting point to draw a vector in several given orientations. The spectral difference between the front pixel of the extension vector and the center pixel is calculated iteratively until the vector stops its extension. The stop rule is that the spectral difference is greater than a given threshold or the vector length reaches a given maximum value. The vector length in all orientations is recorded as the PSI feature. On each orientation, the vector represents the distribution range where pixels have similar spectral features to those of center pixels. However, when PSI is used as the feature to capture the building shape, two problems appear. Firstly, the vector will not stop at the edges where the spectral difference of two side pixels is unobvious. Secondly, this feature is highly susceptible to some irregular spots inside the faces of buildings with a certain difference in spectra. These issues will lead to the consequence that real building edges cannot be reached.

This study proposes an LCS feature to describe the shape of buildings. Its calculating process includes center pixel position judgment, vector generation, vector length computation and shape feature generation.

(1) Center pixel position judgment

If the current center pixel is located in the BCA, then step 2 is performed. Otherwise, the LCS of this center pixel is skipped, and the next pixel is set as center pixel.

(2) Vector generation

The extension orientation is set as D (e.g., all the orientations of yellow arrows in Figure 3a; the number of orientations is set as d). The extended number of steps is initialized as $n_{step}=0$. The initialization starts from the center pixels C (e.g., the pixels labeled as “1” and “2” in Figure 3a), and vectors are drawn along each orientation i ($i\in D$). The stop conditions of the vector extension are as follows:

C1: The next pixel the vector meets belongs to the line segments (e.g., the points on the red line segments in Figure 3a);

C2: $n_{\mathrm{step}}$ equals to the maximum step threshold $T_{\mathrm{step}\text{\hspace{0.05em}}max}$.

If the vector does not stop, then the front pixel of the vector is incorporated into the vector, and $n_{\mathrm{step}}$ is increased by one to continue the extension until reaching the stop condition.

(3) Vector length computation

When all the vectors stop extending, the coordinates of all end pixels of vectors are recorded. The length of vectors is the Euclidean distance between the end pixel and the center pixel (e.g., the length of each yellow arrow in Figure 3a). If the vector does not meet the line segments before the vector length reaches the maximum, then the latter is its final length (e.g., the radius of the blue circle in Figure 3a).

Note that the BCA outline is not used as the stopping condition for the vector extension. The vectors start from the center pixels in the candidate area that may go through the outlines of the area. The pixels on both sides of the outline may belong to the same class; as shown in Figure 2d, most of the BCA outlines pass through the grassland. Accordingly, LCS can reflect the natural shape characteristics of objects.

(4) Shape feature generation

For all the pixels in BCA, the final length of the vector in each orientation $i\in D$ is the LCS feature value, as shown in the green area in Figure 3b. In order to distinguish the building from the ground objects in non-BCA easily, this study assign the LCS value to the pixels in non-BCA. Figure 3b depicts a simple example of value assigning for the pixels of non-BCA. The green area is the BCA, and the yellow area is the non-BCA. Along each orientation, the LCS value of pixels in BCA is obtained through steps 1–3. The maximum LCS value is assigned to all the pixels of non-BCA in the same orientation. Thus, the difference of LCS values between building pixels and the pixels in non-BCA is enlarged.

Steps 1–4 are repeated for all orientations. We can obtain the final LCS feature matrix, which has dimensions of m × n × d, where m and n are the numbers of rows and columns of images, respectively, and d is the number of orientations. The LCS value of all pixels in each orientation can be regarded as an independent shape feature.

Note that many line segments exist near the building; hence, the length of vectors inside the building will not be large in any orientation. As shown in Figure 3a, the vector extension along all orientations for the building pixel labeled 1 is stopped because of the line segments (the red lines in Figure 3a). For the pixels that belong to grass or bare land (the pixel labeled 2 in Figure 3a), the vectors extend along most orientations to reach the maximum length. The likelihood that the length of building pixels’ vectors will be smaller than those of other ground object pixels’ vectors in all orientations is high. As a result, the building’s LCS value has a high likelihood to be small, whereas the likelihood that a pixel in non-BCA belongs to the building is small.

2.3. Feature Vector Construction

Section 2.2.3 indicates that the LCS values of building pixels in all orientations are relatively low in the entire image. However, the LCS values of some ground objects with regular shapes and near to buildings (such as the path-connected building to the main streets) will be similar to those of the buildings. Therefore, the LCS should be combined with other features to be the reference for building change detection. Here, the spectral feature and LCS value are constructed as a feature vector of every object. Spectral feature and LCS are normalized to [0, 1] to unify the dimension. The spectral value of each band in the original image is normalized using the following calculation equation:

$$X_{\mathrm{new}}^{(t)}=X_{\mathrm{old}}^{(t)}/255,$$

(2)

where $X^{(t)}$ is the value of each spectral band; $t=\{1,2\}$ indicates the image’s phase ordinal; and the subscript “old” represents the original data, and “new” represents the data after normalization, the same as below. The equation for LCS normalization is

$${\mathrm{LCS}}_{\mathrm{new}}^{\left(t\right)}{=\mathrm{LCS}}_{\mathrm{old}}^{\left(t\right)}{/\mathrm{LCS}}_{\max },$$

(3)

where ${\mathrm{LCS}}^{\left(t\right)}$, $t=\{1,2\}$ represents the LCS value calculated in two-phase images, and ${\mathrm{LCS}}_{\max }$ is the maximum value of the two-phase LCS value in all orientations.

After the spectral feature and LCS are normalized, all of these features are stacked to form the feature matrix of each phase, denoted as $F^{(t)}$, $t=\{1,2\}$. As shown in Figure 4a, a feature matrix F extracted from an image contains n + d bands, where n is the number of spectral bands and d is the number of orientations. Each object acquires its own feature vector, in which the value of each component is the mean value of all pixels within the object of each band in F.

In addition, an object-based CV is calculated for each object to obtain the change information. The CV value $D_i$ is calculated through the following equation:

$$D_i=\frac{1}{\Vert R_i\Vert \times C}\sqrt{{\displaystyle \sum _{j=1}^C{\displaystyle \sum _{(x,y)\in R_i}{(F_j^{(1)}(x,y)-F_j^{(2)}(x,y))}^2}}},$$

(4)

where C is the dimension of feature matrix F. $F_j^{(1)}(x,y)$ and $F_j^{(2)}(x,y)$ are the values of pixels (x, y) in the j_th band of two-phase feature matrices, respectively. $\Vert R_i\Vert$ is the number of pixels inside $R_i$. As shown in Figure 4b, the feature vector of each object is arranged as

$$v_i=[F_1^{(1)}(R_i),...,F_C^{(1)}(R_i),D_i,F_1^{(2)}(R_i),...,F_C^{(2)}(R_i)],$$

(5)

where $F_j^{(t)}(R_i)$ is the mean value of pixels in object $R_i$ of the j_th band in the t_th phase feature matrix.

2.4. Classification

After the feature vector has been constructed for every object, the logistic regression model [41] is adopted in this study to determine the building change information by implementing a binary classification. This model produces regression coefficients for each variable on the basis of data sampling, and the relationship between independent and dependent variables is analyzed on the basis of these coefficients. The logistic model obtains classification results by using maximum likelihood estimation. It gives a likelihood value which ranges from 0 to 1 to each object in accordance with the object feature vector. When the likelihood value is close to 1, the object is likely to be a changed building.

In the first step of the classification process, training samples need to be collected. To be specific, some typical objects with high homogeneity are selected through visual interpretation. As described above, the BCA is the region where buildings may exist with a large likelihood. On the contrary, the likelihood for the objects in the non-BCA to belong to buildings is small. Therefore, this study obtains a union BCA (UBCA) based on the two-phase BCAs. The training sample-collecting process is shown in Figure 5. The samples are then assigned into negative or positive sample sets $U_0$ and $U_1$. The positive sample sets correspond to the changed building class P; the negative sample sets correspond to another class N including all unchanged ground objects and changed non-building objects. The number of training samples is approximately one-fifth to one-quarter of the total number of objects.

If the objects do not locate in the UBCA, similar to the objects in the blue area in Figure 5, then they are directly categorized as the class N and do not participate in classification. This approach not only reduces the false detection rate but also saves the calculation time.

After the training sample-collecting process, the logistic regression classifier is trained using the collected samples. Then, the classifier gives each object in UBCA a prediction likelihood value according to its feature vector. Finally, as for each object in UBCA, if its prediction likelihood value is greater than 0.5, then the object is assigned to the class P; otherwise, it is assigned to the class N.

3. Results and Discussion

Experiments are conducted on VHR imagery to verify the proposed building change detection method. The LCSs of two datasets are visualized and analyzed. The sensitivity analysis of key parameters is discussed. The advantage of the LCS feature in building change detection is validated through comparison experiments.

3.1. Study Data

Two datasets of WorldView-2 satellite images, which are acquired from the suburbs of Miami, Florida, USA, are used in this study. They have red, green and blue bands with a spatial resolution of 0.31 m. The two-phase images and changed buildings in the two datasets are shown in Figure 6. The two-phase images of dataset 1 were acquired on 7 March 2013 and 22 March 2017. The two-phase images of dataset 2 were acquired on 27 March 2011 and 24 January 2016. From visual interpretation, the changed buildings in the two datasets are newly built ones in the second phase. The numbers of new buildings are 28 and 19 for datasets 1 and 2, respectively. Some non-changed buildings also exist in both datasets, and few spectral differences are observed in the two-phase images. In addition, a number of other ground objects, such as roads, trees and grasslands, are found in the two datasets. Some of the ground objects experienced the change from one class to another.

3.2. Evaluation Metrics

Several widely used evaluation metrics [42], such as recall rate, false detection rate, overall accuracy and kappa coefficient, are introduced to evaluate the accuracy of the experimental results. They are all calculated from the pixel-based confusion matrix with the assumption that only two categories, namely, changed and unchanged pixels, exist in the classification results, as shown in

Table 1. Change detection confusion matrix.

Number of Pixels	Real Changed	Real Unchanged	Total
Detected as changed	True positive (TP)	False positive (FP)	$D_c=TP+FP$
Detected as unchanged	False negative (FN)	True negative (TN)	$D_u=FN+TN$
Total	$T_c=TP+FN$	$T_u=FP+TN$	N

.

$$\mathrm{Recall}\mathrm{rate}:Recall=\frac{TP}{T_{\mathrm{c}}}$$

(6)

$$\mathrm{False}\mathrm{detection}\mathrm{rate}:FDR=\frac{FP}{D_{\mathrm{c}}}$$

(7)

$$\mathrm{Overall}\mathrm{accuracy}:OA=\frac{TP+TN}{N}$$

(8)

$$\mathrm{Kappa}\mathrm{coefficient}:Kappa=\frac{N\times (TP+TN)-(T_c\times D_c+T_u\times D_u)}{N^2-(T_c\times D_c+T_u\times D_u)}$$

(9)

Additionally, the overall thematic accuracy (TA) proposed in [43] is used to further evaluate the result from the object level:

$$TA=\frac{A(E\cap R)}{A(E\cup R)},$$

(10)

where E is the extracted dataset and R is the reference vector layer. A (*) is the area of the object.

3.3. Parameter Setting

Preprocessing operations are as described in [1] to reduce the discrepancies between the two-phase images. Similarly, the present work conducts radiometric calibration to eliminate reflectance differences and co-registration for ensuring the obtainment of the bi-temporal image pixels with the same location.

After the image processing, some parameters are set for conducting the proposed method as follows:

Scale factor $\omega$: This factor exerts a considerable impact on the generation of the BL map and BCA. $\omega$ determines the influence range of each POL. By considering the coverage ratio of BCA, the parameters $\omega$ of the two datasets are all set as 50 in this study. Further sensitivity analysis of the parameters $\omega$ is described in Section 3.5.

Orientation number d: Dense line segments can be generally extracted from buildings; thus, eight orientations are suitable to judge whether a pixel belongs to a building on the basis of LCS value. Therefore, the orientation number d is set to 8, which indicates the orientations $\left[0°,45°,90°,135°,180°,225°,270°,315°\right]$.

Maximum step threshold $T_{\mathrm{step}\max }$: In the process of LCS creation, for the interior pixels of large homogeneous areas, such as bare land and grass, the vectors in all orientations will generally extend until the maximum step value is reached, and the same state will happen at some orientations of roads. Therefore, in order to make the LCS value of buildings to be distinguishing from other ground objects, $T_{\mathrm{step}\max }$ needs to be larger than the diagonal length of the minimum bounding rectangle of the largest building. Accordingly, the $T_{\mathrm{step}\max }$of the two datasets are both set to 250 in accordance with the image resolution and the size of the buildings.

3.4. LCS Effect

Figure 7 shows the result of LSD line segments and the heat map of LCS mean value. From the first and second rows of Figure 7, the result of line segment extraction is close to the actual edges, and the contour of most buildings and the interior ridge lines are efficiently extracted. The heat map based on LCS mean value, the original PSI mean value, and MBI are shown in the third, fourth and fifth rows, respectively.

In all orientations, the LCS values of the pixels in non-BCA are set to the maximum value of BCA. Therefore, the LCS values of objects in non-BCA are the maximum values in the entire map, thereby resulting in crimson color in the heat map. Most of the building area in the heat map is dark blue, which indicates that the LCS value of buildings is small, as shown in the rectangular regions 1–2 in Figure 7 for example. The reason is that the vectors starting from the inner building pixels are always blocked by the line segments, which results in small LCS values along all orientations. On the contrary, the vectors of the pixels of non-building object in BCA are likely to have a long length, which makes the pixels from buildings and non-buildings easy to distinguish.

Since some buildings have minimal variations in spectral characteristics with surrounding objects, the PSI values of building and non-building pixels may be similar. The rectangular regions 3–4 in Figure 7 are taken as examples. The pixels of buildings and the surrounding objects in the PSI heat map are difficult to distinguish. However, for the same region, the result of the LCS feature proposed in this study is better, and most of the interior pixels are deep blue. Unlike the original PSI, LCS can be more easily distinguished with other surrounding objects. As for MBI, the fifth row of Figure 7 illustrates that the range of MBI values inside the building is large and the MBI values of some buildings are similar to the road due to the spectral differences in the interior of buildings. The MBI values of shady sides of buildings are similar to those of the bare land and grassland, as shown in the rectangular regions 5–6 in Figure 7 for example. By contrast, LCS can coarsely exhibit the buildings in the heat map, whereas MBI may miss some part of buildings.

3.5. Parameter Sensitivity Analysis

Parameter ω plays an important role in LCS calculation. This parameter is used to calculate the BL map and BCA of two-phase images, which are critical for the final change detection result. Under several different values of parameter ω, Figure 8 shows the coverage of buildings and the classification result in two-phase images of dataset 2. The first and second rows show the coverage of BCA to building ground truth (including unchanged and changed buildings) in two-phase images. The classification results obtained by the proposed method are shown in the third row. The accuracy evaluation of the change detection results and the coverage percentage of buildings under different ω settings are shown in

Table 2. Accuracy evaluation for different ω settings.

ω	Coverage Ratio in Image 2011	Coverage Ratio in Image 2016	Recall	FDR	OA	Kappa	TA
10	92.51%	92.79%	74.66%	1.25%	96.35%	0.7832	0.6712
50	99.14%	97.33%	87.74%	1.41%	97.51%	0.8618	0.7787
90	99.02%	88.11%	81.22%	1.44%	96.82%	0.8188	0.7187

.

As described in Section 2.2.1, the parameter ω determines the value of R, which can be regarded as the effective influence range of POL. Although numerous POLs can be extracted from buildings, these POLs mainly distribute at the outlines and ridge lines of buildings without any POLs in the interior homogenous areas of buildings. The first and second rows present that, if ω is too small, then the effective influence range R is limited, and the BL values of the pixels in the interior homogenous areas of buildings are small. Accordingly, as the region shown in the rectangular box in the first column of the second row of Figure 8 demonstrates, these pixels are excluded from the BCA. As ω increases, the effective influence range R of each POL and the BL value also increase. At this point, the pixels located in the center of the image will receive a high BL value when ω is very large, even if they are far from the line segments. This condition will lead some part of buildings far from the image center to be missing in the final result, as the region shown in the rectangle in the third column of the second row of Figure 8.

Therefore, if ω is too large or too small, then the coverage rate of BCA to buildings (including changed and non-changed) will decline and further affect the LCS value and the classification results. As shown in Table 2, when ω is set as 50, the BCAs of the two-phase images have the highest coverage ratio, and all the overall accuracy, kappa coefficient and thematic accuracy are the best. The buildings in the circle at the third row of the Figure 8 also show that some of the changed building parts that are not in the UBCA are missed. These missing parts directly affect the accuracy of the final change detection.

3.6. Comparison of Different Features

The combination of features (1) used in the proposed method is compared with three other feature sets (2)–(4) to verify the advantages of the LCS feature. All feature sets are as follows:

(1)

Spectrum + Shape (LCS) + Object (Spectra + Shape) CV

(2)

Spectrum + Object Spectra CV

(3)

Spectrum + Shape (PSI) + Object (Spectra + Shape) CV

(4)

Spectrum + Shape (MBI) + Object (Spectra + Shape) CV

The comparison results are shown in Figure 9; each column represents the final building change detection result of a dataset. The first row shows the change detection result based on feature set (1); the second row shows the change detection result based on spectral feature and its CV value; the third row shows the change detection result based on spectral feature, original PSI feature, and the CV value of these features; the fourth row shows the change detection result based on spectral feature, MBI feature, and the CV value of these features. The accuracy evaluation of the result is shown in

Table 3. Accuracy evaluation for different features.

	Dataset 1					Dataset 2
Feature Sets	Recall	FDR	OA	Kappa	TA	Recall	FDR	OA	Kappa	TA
(1)	91.57%	5.79%	93.97%	0.7061	0.5858	87.74%	1.41%	97.51%	0.8618	0.7787
(2)	48.03%	4.12%	91.42%	0.4637	0.3427	95.67%	19.06%	82.14%	0.4393	0.3521
(3)	74.68%	6.88%	91.4%	0.5713	0.4473	91.03%	6.53%	93.22%	0.6916	0.5731
(4)	83.8%	10.62%	88.86%	0.5261	0.4121	91.57%	17.04%	83.82%	0.4531	0.3612

.

From the second row in Figure 9, many missing parts (for dataset 1) or false alarms (for dataset 2) are observed when using feature set (2). As illustrated by the value in Table 3, the kappa coefficients and thematic accuracy of two datasets using feature set (2) are very low, and none of those exceed 0.5. It indicates that using spectral features only cannot effectively detect all changed buildings. The reason why the feature set (2) cannot clearly distinguish the changed buildings can be mainly traced back to two factors. On the one hand, spectral difference exists among non-changed buildings in two-phase images. On the other hand, the spectral difference caused by changed buildings is close to the spectral difference caused by other changed ground objects.

As for shape feature, just like what we discussed in Section 3.4, the drawbacks of PSI and MBI directly influence the result. Specifically, after the PSI feature is added (as feature set (3)), as shown in the third row of Figure 9, although the results obtained in the two datasets are higher than those using feature set (2), the improvement is limited. The overall accuracy exhibited in Table 3 is even slightly lower than that of feature set (2) for dataset 1, in which the PSI value of buildings is similar to that of other ground objects, such as bare land. Hence, as shown in the third row of Figure 9, this part of the building pixels are missing (e.g., circles 1–2), and some ground objects with a similar PSI value as buildings are incorrectly detected (e.g., circle 3).

As for the MBI in feature set (4), as shown in the fourth row of Figure 9, not only buildings but also some high-brightness objects with regular shape easily obtain high MBI values. As the region shown in the circles 4–5 in the fourth row of Figure 9 demonstrates, a large area of roads is incorrectly detected, thereby reducing the detection accuracy. Besides, some of the non-changed buildings are also incorrectly detected because of the spectral differences in two-phase images. As given by the value in Table 3, the kappa coefficients and thematic accuracy of two datasets using feature set (4) are lower than those created by feature set (3).

By contrast, the results of feature set (1) used in this study are relatively better than those of feature sets (2)–(4). It can be known from Table 3 that our proposed method acquires high recall rate results with low false-detection rate. For the overall accuracy, kappa coefficient and thematic accuracy, the feature set (1) that uses the proposed LCS as shape feature also obtains the highest value. From the first row in Figure 9, on the one hand, this result illustrates the important role of shape feature in the classification process. In the area with large intraclass spectral differences and small interclass spectral differences, shape features should be used to extract building location information. On the other hand, unlike PSI and MBI, the proposed LCS presents a better result, which proves its superiority in capturing building shape.

4. Conclusions and Future Work

This study utilizes shape feature and OBIA to detect building change detection from VHR remote sensing imagery. Rather than directly modeling building structure, this study represents a shape feature of buildings named as LCS by using line segments. As this feature has the ability of capturing the characteristics of buildings, it has the advantage of individual building change detection in VHR remote sensing imagery, especially in a sparse building region. Furthermore, for a large study area with dense residential zones in VHR imagery, the proposed strategy of change detection can be transferred to extract the change information on the level of building area. Experiments verify the effectiveness and superiority of the LCS feature in a building change detection task over PSI and MBI.

A satisfactory change detection result mainly depends on the features and classification. However, in complex urban environments, it is possible to extract dense lines from some non-building objects, such as roads with shoulders and lanes. These objects can also obtain high LCS values, which will confuse the building change detection to a certain extent. Thus, a highly robust feature representation for various buildings in complex environments will be developed in the future work to extend the generalization of the change detection method.