1. Introduction
Learning on unstructured data is a crucial and interesting problem [
1] that is relevant to many tasks with a spatial nature such as route planning, vehicular demand prediction, understanding disease spread (epidemiology), semantic enrichment of spatial networks, and autonomous robotics [
2,
3,
4,
5,
6,
7,
8]. These tasks could be modelled using graphs. Traditional neural learning approaches such as Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs) have been successfully applied to solving challenging vision and machine translation problems among many others [
9,
10]. However, they are designed for regular grids or euclidean structures. Hence, a key motivation for Graph Neural Networks (GNNs) is the need for models that can learn on irregular structures such as graphs. In this regard, GNNs can encode the neighbourhood relational constraints (relational inductive bias) between graph entities such as nodes or edges during learning [
1]. Generally, GNNs work by exploiting local graph information, which is achieved either through message-passing or aggregating information from neighbours using an embedding [
11,
12].
Local here refers to the neighbourhood of a graph node. For example, in a street network where street segments are nodes, the locality of a street segment is the set of streets that have a connection to that street. In this paper, we restrict the locality to one-hop neighbours, i.e., a direct connection. The exploitation of local graph information is typically implemented at the cost of disregarding the global graph structure. Granted, this approach is largely influenced by structural assumptions about the graphs such as homophily and unbiased class distributions [
11,
12]. Consequently, this poses two possible limitations. Firstly, model capacity could be impacted by the disregard for the global graph structure. Secondly, GNNs could fail to generalise well on noisy real-world graphs such as spatial graphs where these assumptions may not be sufficiently held.
In this article, we consider street networks as spatial networks. Generally, graphs are deemed unstructured in the sense that topological features such as node degree are unbounded. However, this is not necessarily the case for street networks as there can only be a certain number of streets adjacent to one street. In addition, street networks are less dense than traditional networks. For example, the average degree of street networks in Los Angeles, Rome, and Vancouver are 4.47, 4.13, and 4.98 respectively. In comparison, a citation network, a social network and protein-protein interaction (PPI) graphs have an average degree of 9.15, 492, and 28.8 respectively [
13]. Furthermore, street networks exhibit
volatile homophily [
14]. This phenomenon can be better understood through the concept of
spatial polycentricity [
15,
16]. Using the distribution of street types across a city as an example, spatial polycentricity suggests that the street network of a city would not necessarily have the street classes clustered in sub-structures, hereby contradicting the general definition of homophily. In the same vein, street networks exhibit high class imbalance, with differences between two classes being as high as three orders of magnitude [
7]
GNNs can be susceptible to overfitting and tend to be unpredictable when applied to real-world graphs [
17,
18]. This limitation is amplified when we consider the already discussed conflict between implementational assumptions of GNNs and the characteristics of street networks, especially in light of the extremely high variance between class distributions that exist in many spatial networks [
7]. Thus, in this article, we study GNNs for node classification on street networks. Specifically, we seek to investigate the relationship between two pertinent characteristics of spatial networks to GNNs. These characteristics are a
global graph structure and
biased class distributions. Consequently, we formulate the following questions:
How well do vanilla GNNs generalise on imbalanced spatial graphs?
Can the performance of GNNs be improved by encoding knowledge about the global structure of the spatial networks?
Can the generalisation capacity of GNNs be improved for imbalanced spatial graphs when global structure is accounted for?
These questions are addressed in
Section 7. We design our problem as a multi-class node classification one for graphs that are highly imbalanced. Specifically, we focus on the open research problem of enriching the semantics of spatial networks [
7,
8]. In this regard, we propose a new sampling approach: Structure-Aware Sampling (SAS), which encodes the global graph structure in the model by leveraging the
intra-class and
global-geodesic distances between nodes. We develop a neural framework using this sampling technique to train a model for spatial graphs. We evaluate our proposal against state-of-the-art methods on large real-world spatial graphs. Our results show a clear improvement in the majority of cases, with as much as a 20% F1-score improvement on average over traditional methods. Our approach is summarised in
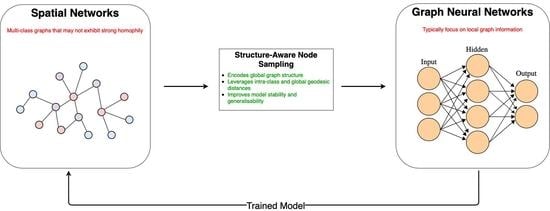
Figure 1.
We summarise our contributions succinctly:
We show that vanilla GNNs fail to generalise sufficiently for imbalanced spatial graphs;
We propose a new sampling technique (SAS) for training GNNs for spatial networks, which significantly improves model capacity;
We demonstrate that encoding graph structure (via our sampling technique) to train GNNs improves the generalisability of models by an average F1-score of 20%, even with class imbalance.
The remainder of this article is organised as follows: In
Section 2, we describe related themes and approaches. Preliminaries are defined and the problem formulated in
Section 3. We describe our approach in
Section 4 and experimental methodology in
Section 5. We present and discuss our results in
Section 6. We summarise our conclusions in
Section 7.
7. Conclusions
In this article, we proposed a novel approach to sampling nodes when training Graph Neural Networks for spatial graphs. This work is motivated by a need to improve the generalisability of GNNs for noisy real-world graphs. Subsequently, the approach proposes to achieve this by encoding global graph structure into the model development process. It was implemented by leveraging the structure of the graph using
intra-class and
global-geodesic distances. The problem was formulated as a node classification with one for noisy, biased, and multi-class graphs. The approach was evaluated on three large real-world datasets that have a high variance between class sizes. Our evaluations showed that our sampling approach was able to mitigate the problem of over-fitting and over-smoothing observed in GNNs. In addition, we determined that our technique leads to a more generalisable model. Consequently, we addressed the questions posed in
Section 1: (1) Vanilla GNNs do not generalise well on spatial graphs, at least not when compared to an approach using global structure. (2) The performance of GNN models could improve significantly when global structure is taken into consideration. (3) The generalisation capacity of GNN models can be improved when a global graph structure is considered.
The significance of our results is appreciated in light of the recent interest in graph neural methods among researchers. A limitation of traditional machine-learning methods is that they assume independence between entities. This makes them unsuitable in situations where entities share a relationship (i.e., exhibit dependence). Graph Neural Networks (GNNs) bridge this gap by preserving the relational dependence between entities during learning. However, the focus of GNNs on local neighbourhood with disregard for global structure could hamper model robustness for spatial graphs. We believe that our work in this article will inspire a broader investigation into improving GNNs for spatial tasks. In this article, we demonstrated the importance of global structure for learning on spatial graphs. For future work, we will investigate the transferability of our method across street networks.