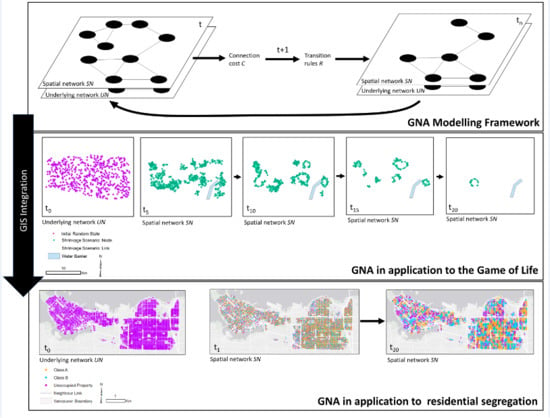
Representing Complex Evolving Spatial Networks: Geographic Network Automata
Abstract
:1. Introduction
2. Geographic Network Automata (GNA)
2.1. GNA Modeling Framework
2.2. GNA Spatial Network Analysis using Graph Theory
3. Geographic Network Automata Case Studies
3.1. GNA Game of Life GNAGOL
3.1.1. GNAGOL Modelling Framework
3.1.2. GNAGOL Scenarios
3.1.3. GNAGOL Results
GNAGOL Simulation Results
GNAGOL Spatial Network Analysis Results
3.2. GNA Schelling’s Segregation GNASEG
3.2.1. GNASEG Modelling Framework
3.2.2. GNASEG Results
GNASEG Simulation Results
GNASEG Spatial Network Analysis Results
4. Discussion and Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Scellato, S.; Noulas, A.; Lambiotte, R.; Mascolo, C. Socio-spatial properties of online location-based social networks. Proceedings of Fifth International AAAI Conference on Weblogs and Social Media, Barcelona, Spain, 17–21 July 2011; pp. 329–336. [Google Scholar]
- Zhong, C.; Arisona, S.M.; Huang, X.; Batty, M.; Schmitt, G. Detecting the dynamics of urban structure through spatial network analysis. Int. J. Geogr. Inf. Sci. 2014, 28, 2178–2199. [Google Scholar] [CrossRef]
- Fortuna, M.A.; Gómez-Rodríguez, C.; Bascompte, J. Spatial network structure and amphibian persistence in stochastic environments. Proc. R. Soc. B Biol. Sci. 2006, 273, 1429–1434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koylu, C.; Guo, D. Smoothing locational measures in spatial interaction networks. Comput. Environ. Urban Syst. 2013, 41, 12–25. [Google Scholar] [CrossRef]
- Sarkar, D.; Andris, C.; Chapman, C.A.; Sengupta, R. Metrics for characterizing network structure and node importance in Spatial Social Networks. Int. J. Geogr. Inf. Sci. 2019, 33, 1017–1039. [Google Scholar] [CrossRef]
- Gross, T.; Sayama, H. Adaptive networks. In Adaptive Networks: Theory, Models and Applications; Gross, T., Sayama, H., Eds.; Springer: Heidelberg, Germany, 2009; pp. 1–8. [Google Scholar]
- Bansal, S.; Read, J.; Pourbohloul, B.; Meyers, L.A. The dynamic nature of contact networks in infectious disease epidemiology. J. Biol. Dyn. 2010, 4, 478–489. [Google Scholar] [CrossRef]
- Balcan, D.; Colizza, V.; Gonçalves, B.; Hu, H.; Ramasco, J.J.; Vespignani, A. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl. Acad. Sci. USA 2009, 106, 21484–21489. [Google Scholar] [CrossRef] [Green Version]
- Smith, D.M.; Onnela, J.-P.; Lee, C.F.; Fricker, M.D.; Johnson, N.F. Network automata: Coupling structure and function in dynamic networks. Adv. Complex Syst. 2011, 14, 317–339. [Google Scholar] [CrossRef] [Green Version]
- Barthelemy, M. Morphogenesis of Spatial Networks; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- O’Sullivan, D. Toward micro-scale spatial modeling of gentrification. J. Geogr. Syst. 2002, 4, 251–274. [Google Scholar] [CrossRef]
- Urban, D.; Keitt, T. Landscape connectivity: A graph-theoretic perspective. Ecology 2001, 82, 1205–1218. [Google Scholar]
- Ducruet, C.; Notteboom, T. The worldwide maritime network of container shipping: Spatial structure and regional dynamics. Glob. Netw. 2012, 12, 395–423. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B. Street hierarchies: A minority of streets account for a majority of traffic flow. Int. J. Geogr. Inf. Sci. 2009, 23, 1033–1048. [Google Scholar] [CrossRef]
- Bian, L.; Liebner, D. A network model for dispersion of communicable diseases. Trans. GIS 2007, 11, 155–173. [Google Scholar] [CrossRef]
- Colizza, V.; Barrat, A.; Barthélemy, M.; Vespignani, A. The role of the airline transportation network in the prediction and predictability of global epidemics. Proc. Natl. Acad. Sci. USA 2006, 103, 2015–2020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boccara, N.; Cheong, K. Critical behaviour of a probabilistic automata network SIS model for the spread of an infectious disease in a population of moving individuals. J. Phys. A Math. Gen. 1993, 26, 3707. [Google Scholar] [CrossRef]
- Boccara, N.; Roblin, O.; Roger, M. Automata network predator-prey model with pursuit and evasion. Phys. Rev. E 1994, 50, 4531. [Google Scholar] [CrossRef]
- Sayama, H.; Laramee, C. Generative network automata: A generalized framework for modeling adaptive network dynamics using graph rewritings. In Adaptive Networks: Theory, Models and Applications; Gross, T., Sayama, H., Eds.; Springer: Heidelberg, Germany, 2009; pp. 311–332. [Google Scholar]
- Conway, J. The game of life. Sci. Am. 1970, 223, 4. [Google Scholar]
- Schelling, T.C. Models of segregation. Am. Econ. Rev. 1969, 59, 488–493. [Google Scholar]
- Schelling, T.C. Dynamic models of segregation. J. Math. Sociol. 1971, 1, 143–186. [Google Scholar] [CrossRef]
- Anderson, T.; Dragicevic, S. A Geographic Network Automata approach for modelling dynamic ecological systems. Geogr. Anal. 2020, 52, 3–27. [Google Scholar] [CrossRef]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef] [Green Version]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef] [Green Version]
- Lewis, T.G. Network Science: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Barabási, A.-L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.-U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Erdős, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960, 5, 17–60. [Google Scholar]
- Dall, J.; Christensen, M. Random geometric graphs. Phys. Rev. E 2002, 66, 016121. [Google Scholar] [CrossRef] [Green Version]
- Antonioni, A.; Tomassini, M. Degree correlations in random geometric graphs. Phys. Rev. E 2012, 86, 037101. [Google Scholar] [CrossRef] [Green Version]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabási, A.-L. Diameter of the world-wide web. Nature 1999, 401, 130–131. [Google Scholar] [CrossRef] [Green Version]
- Cohen, R.; Erez, K.; Ben-Avraham, D.; Havlin, S. Resilience of the internet to random breakdowns. Phys. Rev. Lett. 2000, 85, 4626. [Google Scholar] [CrossRef] [Green Version]
- Udny Yule, G. A mathematical theory of evolution, based on the conclusions of Dr. JC Willis, FRS. Philos. Trans. R. Soc. Lond. Ser. B 1925, 213, 21–87. [Google Scholar]
- Jeong, H.; Néda, Z.; Barabási, A.-L. Measuring preferential attachment in evolving networks. EPL (Europhys. Lett.) 2003, 61, 567. [Google Scholar] [CrossRef] [Green Version]
- D’souza, R.M.; Borgs, C.; Chayes, J.T.; Berger, N.; Kleinberg, R.D. Emergence of tempered preferential attachment from optimization. Proc. Natl. Acad. Sci. USA 2007, 104, 6112–6117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simphony, R. Repast Simphony Version 2.4; University of Chicago: Chicago, IL, USA, 2016. [Google Scholar]
- Van Wijk, B.C.; Stam, C.J.; Daffertshofer, A. Comparing brain networks of different size and connectivity density using graph theory. PLoS ONE 2010, 5, e13701. [Google Scholar] [CrossRef] [PubMed]
- Arribas-Bel, D.; Nijkamp, P.; Poot, J. How diverse can measures of segregation be? Results from Monte Carlo simulations of an agent-based model. Environ. Plan. A Econ. Space 2016, 48, 2046–2066. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Vainchtein, D.; Weiss, H. Schelling’s segregation model: Parameters, scaling, and aggregation. Demogr. Res. 2009, 21, 341–366. [Google Scholar] [CrossRef]
- Benenson, I.; Omer, I.; Hatna, E. Entity-based modeling of urban residential dynamics: The case of Yaffo, Tel Aviv. Environ. Plan. B Plan. Des. 2002, 29, 491–512. [Google Scholar] [CrossRef]
- Flint Ashery, S. Schelling-type micro-segregation in a Hassidic enclave of Stamford-Hill. Hous. Stud. 2018, 33, 1038–1059. [Google Scholar] [CrossRef]
- Perez, L.; Dragicevic, S.; Gaudreau, J. A geospatial agent-based model of the spatial urban dynamics of immigrant population: A study of the island of Montreal, Canada. PLoS ONE 2019, 14, e0219188. [Google Scholar] [CrossRef]
- Fagiolo, G.; Valente, M.; Vriend, N.J. Segregation in networks. J. Econ. Behav. Organ. 2007, 64, 316–336. [Google Scholar] [CrossRef] [Green Version]
- Banos, A. Network effects in Schelling’s model of segregation: New evidence from agent-based simulation. Environ. Plan. B Plan. Des. 2012, 39, 393–405. [Google Scholar] [CrossRef] [Green Version]
- Netto, V.M.; Soares, M.P.; Paschoalino, R. Segregated networks in the city. Int. J. Urban Reg. Res. 2015, 39, 1084–1102. [Google Scholar] [CrossRef]
- Cui, Z.; Hwang, Y.-A. House exchange and residential segregation in networks. Int. J. Game Theory 2017, 46, 125–147. [Google Scholar] [CrossRef]
- Benenson, I.; Torrens, P. Geosimulation: Automata-based Modeling of Urban Phenomena; John Wiley & Sons: West Sussex, UK, 2004. [Google Scholar]
- Torrens, P.M.; Benenson, I. Geographic automata systems. Int. J. Geogr. Inf. Sci. 2005, 19, 385–412. [Google Scholar] [CrossRef] [Green Version]
- White, R.; Engelen, G. High-resolution integrated modelling of the spatial dynamics of urban and regional systems. Comput. Environ. Urban Syst. 2000, 24, 383–400. [Google Scholar] [CrossRef] [Green Version]
- Crooks, A.; Castle, C.; Batty, M. Key challenges in agent-based modelling for geo-spatial simulation. Comput. Environ. Urban Syst. 2008, 32, 417–430. [Google Scholar] [CrossRef] [Green Version]
- Torrens, P.M. Agent-based models and the spatial sciences. Geogr. Compass 2010, 4, 428–448. [Google Scholar] [CrossRef]
- White, R.; Engelen, G. Cellular automata as the basis of integrated dynamic regional modelling. Environ. Plan. B Plan. Des. 1997, 24, 235–246. [Google Scholar] [CrossRef]
- Batty, M.; Xie, Y.; Sun, Z. Modeling urban dynamics through GIS-based cellular automata. Comput. Environ. Urban Syst. 1999, 23, 205–233. [Google Scholar] [CrossRef] [Green Version]
- Gimblett, H.R. Integrating Geographic Information Systems and Agent-Based Modeling Techniques for Simulating Social and Ecological Processes; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- DeAngelis, D.L.; Mooij, W.M. Individual-based modeling of ecological and evolutionary processes. Annu. Rev. Ecol. Evol. Syst. 2005, 36, 147–168. [Google Scholar] [CrossRef]
- O’Sullivan, D. Graph-cellular automata: A generalised discrete urban and regional model. Environ. Plan. B Plan. Des. 2001, 28, 687–705. [Google Scholar] [CrossRef] [Green Version]
- Blumenfeld-Lieberthal, E.; Portugali, J. Network cities: A complexity-network approach to urban dynamics and development. In Geospatial Analysis and Modelling of Urban Structure and Dynamics; Jiang, B., Yao, X., Eds.; Springer: New York, NY, USA, 2010; pp. 77–90. [Google Scholar]
- Pires, B.; Crooks, A.T. Modeling the emergence of riots: A geosimulation approach. Comput. Environ. Urban Syst. 2017, 61, 66–80. [Google Scholar] [CrossRef]
- Anderson, T.M.; Dragićević, S. Network-agent based model for simulating the dynamic spatial network structure of complex ecological systems. Ecol. Model. 2018, 389, 19–32. [Google Scholar] [CrossRef]
- Anderson, T.; Dragicevic, S. NEAT approach for testing and validation of geospatial network agent-based models. Int. J. Geogr. Inf. Sci. 2020, in press. [Google Scholar] [CrossRef] [Green Version]







| Stage | Description |
|---|---|
| 1. Conceptualize system of interest as spatial network SN | Define • the components that make up the systems of interest to be represented as nodes • the interactions, flows, and relationships to be represented as links • the node and link spatial, non-spatial, and topological attributes Determine • whether the phenomenon is best represented by a weighted or directional network whether there is an underlying network UN structure that influences the spatial network SN and vice versa Consider the scale at which the system has been abstracted and the limitations |
| 2. Identify important graph theory measures | Identify which global or local graph theory measures are valuable to measure the spatial or non-spatial characteristics of the evolving spatial network SN. This is a function of the purpose of the model. |
| 3. Determine the neighborhood J | Determine which t nodes are within the neighborhood of node based on distance, weight, cost, and/or probability |
| 4. Develop transition rules | Develop the rules representing interactions between neighboring nodes that result in network evolution i.e., change of state, location, or connectivity of nodes |
| 5. Develop connection costs | Identify influences that the matrix has on network structure i.e., geographic barriers, distance thresholds, cost surface |
| 6. Implement the GNA | Input geospatial datasets to represent geographic barriers, cost surface analysis, underlying network UN structures, and/or initial spatial network SN Develop • georeferenced node automata and link objects based on conceptualization • programming functions that implement transition rules and connection costs • programming functions that calculate local and global graph theory measures |
| 7. Test the GNA | Perform sensitivity testing, model calibration, and validation using independent datasets |
| 8. Execute model and scenarios | Execute model and scenarios for the necessary number of time steps |
| 9. Apply graph theory to characterize network structures | Execute developed programming functions that calculate local and global graph theory measures to enhance the understanding of the phenomena being simulated, to compare network structures as the network evolves, or to compare network structures between scenarios |
| Property Type | Description | Examples of Node Properties | Examples of Link Properties |
|---|---|---|---|
| Spatial | Geometric properties pertaining to the node v or link l | Location (x, y coordinates), area, distance from, perimeter | Length, coordinates of end points, direction |
| Non-Spatial | Qualitative and quantitative non-spatial attributes pertaining to the node v or link l | Name, ID, color, value, type, state | Name, ID, color, value, type, state |
| Network | Measurements derived from network theory pertaining to the node v or link l | Degree, betweenness, weight, clustering coefficient, list of neighbors | Weight, list of end nodes |
| Graph Theory Measure | Definition |
|---|---|
| Average degree <k> | The number of connections a node has to other nodes in the network is a localized measure, specific to each node, and is referred to as node degree k. Therefore, the mean degree across all nodes in the network is referred to as average degree <k>. |
| Degree distribution P(k) | The fraction of nodes in the network with degree k, calculated for the entire distribution of k is referred to as degree distribution P(k). |
| Average clustering coefficient <C> | Clustering coefficient C measures the likelihood of nodes that are connected to node i are also connected to each other. When C = 1, all nodes connected to node i are also connected to each other and when C = 0, none are connected to each other. This is a localized measure specific to each node. Average clustering coefficient <C> measures the average C across all nodes in the network. |
| Average shortest path length <l> | The average number of intermediate nodes and links in the shortest path between all pairs of nodes in the network is referred to as average path length <l>. |
| Rule | Scenario | Parameter x |
|---|---|---|
| R1. To simulate the dynamics of underpopulation, any live node i with x live neighbors j dies and is removed from the spatial network SN | Scenario 1 | ≤6 |
| Scenario 2 | ≤11 | |
| R2. To simulate the dynamics of survival of the fittest, any live node i with x live neighbors j maintains their alive state and thus their place in the spatial network SN. | Scenario 1 | =7, 8, 13, or 14 |
| Scenario 2 | NA | |
| R3. To simulate the dynamics of overpopulation, any live node i with x live neighbors j dies and is removed from the spatial SN. | Scenario 1 | ≥15 |
| Scenario 2 | ≥20 | |
| R4. To simulate the dynamics of reproduction, any dead node with x live neighbors j becomes a live node and is added to the spatial network SN. | Scenario 1 | >8 and <13 |
| Scenario 2 | >11 and <20 |
| (a) Scenario 1: Network Growth | |||||
| Graph Theory Measure | (1) | (2) | (3) | (4) | (5) |
| (1) Number of Nodes | 1.00 | ||||
| (2) Number of Links | 0.99 | 1.00 | |||
| (3) Average Clustering Coefficient | −0.97 | −0.98 | 1.00 | ||
| (4) Average Path Length | 0.79 | 0.79 | −0.82 | 1.00 | |
| (5) Average Degree | 0.99 | 0.99 | −0.98 | 0.8 | 1.00 |
| (b) Scenario 2: Network Shrinkage | |||||
| Graph Theory Measure | (1) | (2) | (3) | (4) | (5) |
| (1) Number of Nodes | 1.00 | ||||
| (2) Number of Links | 0.94 | 1.00 | |||
| (3) Average Clustering Coefficient | −0.73 | −0.67 | 1.00 | ||
| (4) Average Path Length | 0.74 | 0.94 | −0.58 | 1.00 | |
| (5) Average Degree | 0.99 | 0.95 | −0.72 | 0.74 | 1.00 |
| Graph Theory Measures | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|
| (1) Number of Nodes | 1.00 | |||||
| (2) Number of Links | −0.82 | 1.00 | ||||
| (3) Average Clustering Coefficient | −0.72 | 0.97 | 1.00 | |||
| (4) Average Path Length | 0.42 | −0.74 | −0.80 | 1.00 | ||
| (5) Average Degree | −0.83 | 0.99 | 0.96 | −0.74 | 1.00 | |
| (6) Assortativity | −0.70 | 0.95 | 0.99 | −0.82 | 0.95 | 1.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, T.; Dragićević, S. Representing Complex Evolving Spatial Networks: Geographic Network Automata. ISPRS Int. J. Geo-Inf. 2020, 9, 270. https://doi.org/10.3390/ijgi9040270
Anderson T, Dragićević S. Representing Complex Evolving Spatial Networks: Geographic Network Automata. ISPRS International Journal of Geo-Information. 2020; 9(4):270. https://doi.org/10.3390/ijgi9040270
Chicago/Turabian StyleAnderson, Taylor, and Suzana Dragićević. 2020. "Representing Complex Evolving Spatial Networks: Geographic Network Automata" ISPRS International Journal of Geo-Information 9, no. 4: 270. https://doi.org/10.3390/ijgi9040270
APA StyleAnderson, T., & Dragićević, S. (2020). Representing Complex Evolving Spatial Networks: Geographic Network Automata. ISPRS International Journal of Geo-Information, 9(4), 270. https://doi.org/10.3390/ijgi9040270