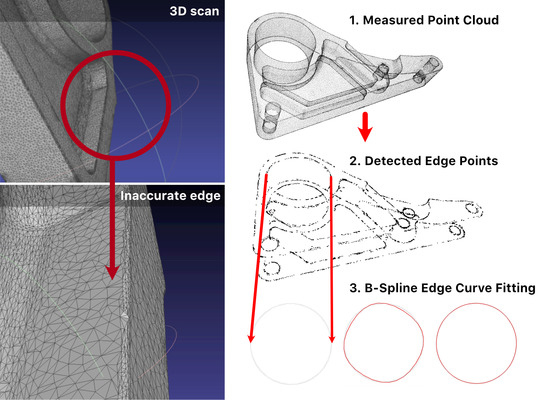
Our work covers the part of automation in manufacturing and reverse engineering for design changes. The widespread availability of cheap commercial depth sensors or multi-camera setups leads to their common usage in manufacturing engineering, especially in rapid product development [
3]. Therefore, the point cloud has become the regular type of the representation used e.g., in reverse engineering (RE) and rapid prototyping (RP). The precision, scanning speed and variety of processing algorithms create suitable conditions for its common usage.
Usually, 3D scanners are provided with software that creates a physical object in the two-phase setup: reconstructing CAD model from the scanned point data, and subsequent STL model output. However, the implemented methods are usually sufficient only for simple and smooth objects. More complex objects with holes, sharp edges or corners often require prior knowledge of how to edit the scanned data. The data post-processing is time-consuming and can potentially lead to errors. We present an algorithm that automatically detects sharp features in arbitrary point cloud data. Our algorithm is based on a modified region-growing method. The input value to the algorithm is only one parameter—the normal vector threshold
(optimal start value and the description is presented in
Section 2.1). Region-growing algorithm eliminates the planar points and the remaining points are probably edge points.
Before the final manufacturing process or 3D printing, a correct model is essential for STL generation [
5] and subsequent slicing [
4,
6].
Figure 2 shows the common problematic part (jagged and inaccurate borders) that occurs frequently. To solve this problem, in
Section 3.2 we propose the novel edge representation based on B-spline approximation. The asymmetric error evaluation is based on bell function with weighting using golden ratio [
7] to improve the edge representation of the models.
Prior Work
Point cloud segmentation and classification plays a key role in point cloud processing in RE/RP usage. Segmentation is the process of grouping point clouds into multiple homogeneous regions with similar properties whereas classification is the step that labels these regions. Segmentation methods are divided into many categories and the choice of the methods depends on the area of interest, sampling density, data quality and explicit structure of point cloud. We can use the categorization described in [
9,
10]: region-growing, edge-based methods, model fitting, and hybrid methods.
Most of the methods start with region growing that was purposed by Besl [
11] for segmentation of images. The region-growing algorithm was later expanded into 3D in two different versions: unseeded [
12] and seeded [
13]. Region growing is applied in plenty of different applications, e.g., extracting features and planar surfaces from 3D outcrop point clouds [
14], surface segmentation, and edge feature lines extraction from fractured fragments of relics [
15] or urban environment modelling [
16] and also 3D city modelling (literature survey e.g., in [
17]).
Region growing is frequently improved. For example, Demaris et al. [
18] detect the closed sharp edges using the region growing with normals given by building a local mesh and least-squares planes through the nearest neighborhood points. The correct edge detection in provided by graph theory (minimum spanning tree). In [
16], region-growing step is performed on an octree-based voxelized input point cloud representation to extract major segments.
The edge-based methods are usually used with point clouds transformed into the range images [
19]. Using the high-level features (scan line grouping technique) as segmentation primitives instead of individual pixels ensure the high computational speed. However, this edge detection is not applicable for noisy data.
Model fitting methods assume that a surface can be described as a composition of simple, canonical geometric shapes (watertight reconstruction). Elementary methods use RANSAC to robustly find planes, spheres, cylinders, cones, and torii [
20]. However, there occurs a problem with noise, any fine-grained details are likely to be treated as noise with the primitive prior, if they are unable to be represented as a union of smaller primitives (a survey is described in [
21]). The partial solution is hybrid methods that employ primitives with other prior [
22].
Region-growing, edge-based methods and model fitting do not need pre-processing, but there exist other segmentation methods based on pre-processing. These algorithms are capable of reconstructing data incompleteness [
23,
24] or construct a triangular mesh of given point cloud [
25,
26,
27]. Afterwards, the formed mesh can be processed using e.g., the discrete differential geometry where local extreme of the surface detect the edge lines [
25] or algebraic methods based on bivariate polynomials [
27]. We must note that some of these methods work with the machine learning methods [
28].
After the point cloud segmentation and classification, we need a correct model representation and tessellation (usually STL) with subsequent slicing to extract layer-based additive manufacturing [
29]. There exist various approaches that combine different technologies. Traditional STL approach is described e.g., in [
30]. B-spline or NURBS surfaces are used frequently, e.g., authors in [
31,
32] presents direct slicing from NURBS without STL. Also, B-Rep model composed of planes, spheres, cylinders and cones from a 3D mesh is fitting for slicing [
33,
34]. Some of the authors omit the model reconstruction and make the direct generation of sectional contour. For example, authors in [
35] employ the curve skeleton of the model to slice through the surface mesh edges. B-spline curve fitting of the layers where the curve curvature is determined by a circle fitting procedure is presented in [
8].
The development of neural networks and deep learning also touches the research in point cloud analysis. Some methods are promising but there is still no one-size-fits-all approach. Reviews of the methods are covered e.g., in [
36,
37,
38].
Present literature contains most of the recently known principles. Main scientific contribution is in their improvements and applications. For example, work [
39] (published 2020) uses B-spline representation and normal computation using normal curvature directly computed by partial derivatives of the surface. The omitting of the pre-defined threshold value is the main idea in [
40] (published 2019). The authors suggest the composition of spatial FFT-based filtering and boundary detection, which together allow for direct generation of low noise tessellated surfaces from point cloud data. Ref [
41] presents the feature sensitive point cloud simplification that is based on insensitive support vector regression.
The advantages of the well-known methods (region-growing or PCA) are obvious—robustness, computed easiness, stable algorithms. Because of that, we chose these classical methods and our main idea was (1) the simplification and automatic setting of input values (described in
Section 2.1) (2) find optimal error evaluation in B-spline representation that is suitable for engineering objects. The problem of error computation is described in
Section 2.2 and we proposed asymmetric weighting based on golden ration.