Spatial Analysis of Asymmetry in the Development of Tourism Infrastructure in the Borderlands: The Case of the Bystrzyckie and Orlickie Mountains

Abstract

This paper discusses the issue of analyzing the development of cross-border tourism infrastructure in the borderlands of countries with diversified administrative divisions and spatial databases, which hinders the use of national statistical units for comparative research. As an example, the ability to use the square grid and kernel density estimation methods for the analysis and spatial visualization of the level of tourism infrastructure development is studied for the Orlickie and Bystrzyckie Mountains, located in the Polish–Czech border area. To synthetically assess and compare the level of diversity, the methodology used in the Human Development Index was adapted using selected component indicators calculated for a square grid clipped to the boundaries of the area under study. This analysis enabled us to quantify the asymmetry in the development of tourism infrastructure in the borderlands via the calculation of the synthetic infrastructure development index. This index is 1.29 times higher in the Czech than in the Polish border area. However, the spatial concentration analysis of infrastructure shows that the diversity in the study area can be assessed as higher than the results using the average density indicators. This paper also discusses the benefits and problems associated with using the square grid method for the representation and analysis of heterogeneous data on tourism infrastructure in two neighboring national states.

1. Introduction

Comparative studies of the spatial diversity of borderlands development, including land use, infrastructure, and tourism issues, are common [1,2,3]. This also applies to the Polish–Czech border, which is increasingly the subject of cross-border analyses. These analyses are not limited to an area located in one country but examine the entire functional regions crossed by state borders [4,5]. Thanks to the democratic changes in the early 1990s and the inclusion of Poland and the Czech Republic (established in 1993) into the European Union (EU) in 2004 and into the Schengen Area in 2007, the state border is usually only administrative [6]. This is conducive to socio-economic development based on tourism [7] and to the cross-border cooperation of local communities [8,9,10].

While examining the adjacent areas located on both sides of the state border operating under different administrative and legal conditions, we encountered limitations related to the lack of homogeneous statistical data for comparative studies, including the problem of the differences in administrative divisions. On a small scale (i.e., for relatively large areas), this type of analysis is usually performed based on data aggregated into statistical units that often correspond to the administrative ones [1,5,11]. However, in the case of large-scale data (i.e., for local areas) or significant differences in the administrative divisions of the neighboring countries covered by the analysis, there are growing research problems that can prevent data collection for methodical comparative studies. Another possible difficulty is the irregular shape of the administrative–statistical units, which makes geographical interpretation difficult. In this case, it may be helpful to use grid cells and choropleth (or “chorodot”) maps to present the spatial diversity of the analyzed phenomenon [12,13], as well as geostatistical analysis methods [14]. However, not using typical administrative statistical units creates problems related to the need to obtain data and calculate one’s own indicators for the adopted research fields [15,16].

The difficulty in acquiring comparable data from neighboring countries is the reason why much cross-border research, including that based on statistics from administrative units, was previously carried out only on one side of the border [1,17]; authors have also used diverse data and methods for adjoining national borderlands [18]. Our paper complements the research conducted by other authors on the development of the Polish–Czech borderland.

The aim of this research paper is to present the basic problems and possibilities of conducting a spatial analysis of tourism infrastructure development in the cross-border region, focusing on the use of the square grid method. The analyzed region is the massif of the Orlickie Mountains (Orlické hory) and Bystrzyckie Mountains located on the border between Poland and the Czech Republic in the Sudetes (Sudety Mountains). The adopted hypothesis proposes that in the studied area, tourism infrastructure will be noticeably better developed in the Czech part of the research area, which was suggested by the historical studies and developmental analyses conducted on both sides of the border of the Sudetes [4,19,20]. We used the square grid methods, modified for our comparative analysis of two adjacent and irregularly shaped border areas; infrastructure density component indicators; and the synthetic index measure used in the Human Development Index method. We complemented our research with a hotspot analysis using the kernel density estimation (KDE) method, Lorenz curve, and Gini coefficient to assess the spatial concentration of the analyzed tourism infrastructure. We also discuss some problems in obtaining and importing publicly available data to perform spatial analysis as a part of research.

In the remainder of this work, we present a review of the literature on the asymmetry of infrastructural development in border areas and basic information on the INSPIRE initiative to create an international spatial database. Then, we explain the assumptions and methods used in our case study. We focus particularly on the utility of the square grid method for the spatial analysis of tourism infrastructure. After presenting the results of the comparative research, we discuss the problems we encountered related to the collection and analysis of the spatial data. Finally, we present our conclusions regarding the possibility to engage in comparative tourism infrastructure research on the borderlands of the two neighboring countries.

Tourism development is a significant issue in spatial and economic studies as tourism is often an important goal for local communities and local governments [21,22,23], especially in the Polish–Czech border areas of the Sudetes [20,24,25]. Therefore, the present results could be useful for researchers and public offices involved in the analysis of the development of cross-border areas, especially where there are difficulties in obtaining homogenous statistical data for borderlands.

2. Research of Infrastructure Development Asymmetries in Border Areas

The problem of symmetry or asymmetry in social development (including migration and population) and the economy (including entrepreneurship and technical infrastructure) is a frequently raised issue in research conducted on borders and border areas [26,27,28,29]. According to Rietveld [30], a national border is a barrier where one can observe a sudden decrease in the interaction intensity between two places. He claims that phenomena such as national regulations (taxes or other law constraints), consumer preferences for domestic products or travel destinations; different public and private management centers; a lack of information about neighboring countries; and higher transport or communication costs in the case of customs or passport control cause visible differences in the infrastructure development in borderlands. As a result of this impact on the state borders of the surrounding areas, issues of development for various types of border and cross-border infrastructures are frequently discussed research topics [31,32], including issues of tourism infrastructure and tourism development in these areas [1,6,33]. These issues are also particularly important for the spatial and investment policies of public local authorities in these areas [34,35,36].

This paper refers to the concept of tourism development, which is not uniformly defined in the literature. According to Rogalewski [37], “tourism development” can be defined as “activities aimed at adapting the geographical environment to the needs of tourism”, which in turn requires the definition of “tourism”. The United Nations World Tourism Organization defines tourism broadly as “a social, cultural and economic phenomenon which entails the movement of people to countries or places outside their usual environment for personal or business/professional purposes” [38]. Difficulties in the formulation of this concept arise from the fact that tourism occurs in various forms and is associated with many phenomena, including economic, cultural, and social issues [39,40]. For this reason, it is also difficult to determine a clear definition for tourism infrastructure in the literature [41], especially since most types of infrastructure can perform various functions in the economy, not just touristic ones. Infrastructure is generally divided into technical (including roads, water supply, and communication) and social (devices and institutions related to culture, education, health, administration, etc.) elements [42,43]. In the case of tourism infrastructure, most authors focus on four types [37,41,42]: (1) accommodation facilities, (2) gastronomic (catering) facilities, (3) communication (roads and public transport facilities), and (4) accompanying facilities (recreational, information, etc.). These are key elements without which it would be difficult to discuss economic development based on tourism. Without transport infrastructure (roads, railways, air transport, etc.), tourists would not be able to reach their destinations. Gastronomic facilities (restaurants, bars, pubs etc.) satisfy the basic and amusement needs of tourists. Accommodation facilities (hotels, motels, hostels, spas, campsites, etc.) are necessary if the trip lasts more than a day. Although the components of tourism infrastructure are important, the accompanying facilities (tourist information points, marked tourist routes and paths, ski routes and ski lifts, museums, sport and recreation facilities, and others) usually determine to a greater extent whether a given area is attractive for tourists [44]. It should also be remembered that attractiveness of an area for tourists is influenced both by anthropogenic elements that can be included in the infrastructure category and by non-material cultural resources (e.g., folk customs) and natural elements (landform, geological sites, and the world of plants and animals), which are not usually considered as infrastructure but are often the main factors for the development of tourism in a given area [45,46]. In this paper, we deliberately focus on technical infrastructure, which is complementary to the existing natural and anthropogenic objects constituting the main tourist attractions (landscape, nature, parks, etc.).

The analysis of tourism’s technical infrastructure in the borderlands requires the collection of spatial data from both areas. The ability to acquire and integrate this information is becoming key problem. For data collected using different data models, the overall analysis requires a transformation process for unification. The issues of spatial information in the European Union (EU) are regulated by the INSPIRE directive, which was adopted by the European Parliament on March 14, 2007 [47]. Its main goal is to provide universal access to spatial information in Europe by establishing a Spatial Data Infrastructure (SDI) [48,49]. The construction of the European SDI is based on infrastructures created and maintained by EU Member States. The basic goal of building national spatial data infrastructures is to facilitate access to spatial data among citizens of a given country, public administration, commercial companies, and others [50]. Many dimensions of activities relate to the aims of this directive, including legal, organizational, and technical issues [49]. Numerous documents are associated with the INSPIRE directive, including ordinances, decisions, data specifications, technical reports, and many others. One of the most crucial tasks in INSPIRE implementation is data harmonization, which can be described as “technical, organizational and legal actions aimed at achieving mutual coherence of spatial data sets and geoinformation services” [51]. The data to be included in the SDI must be provided in a coherent way. The INSPIRE directive defines 34 spatial data themes, including several related to tourism, such as addresses, buildings, protected sites. A technical specification was created for each theme to describe in detail the principles of harmonizing and publishing spatial data. The INSPIRE directive mandates that member states publish spatial data related to the above-mentioned themes using network service standards such as the Web Map Service (WMS) or Web Feature Service (WFS) and provide metadata describing spatial data in catalogue services. Tourism is not directly covered by the INSPIRE themes. Therefore, spatial data, such as data on tourist routes and accommodation facilities in the border areas, are collected and published through various systems. However, on the Polish–Czech border, there are some local initiatives in cross-border national parks whose aim is to harmonize spatial data (e.g., “Karkonosze/Krkonoše in INSPIRE. Common GIS for nature protection” [52]).

The problems in obtaining uniform data mean that analyses on the Polish–Czech borderland have, to date, been carried out only to a limited extent—they usually focused on social phenomena, such as demographic phenomena, and unemployment [5,53], for which data are most easily available. Until now, many such studies covered only one side of the border [18,54] and were typically based on qualitative (descriptive) methods [20,25,55,56]. Some analyses focused on showing differences in statistical data from different sources on both sides of the border [57]. Issues related to developing linear infrastructure, such as roads, have rarely been implemented using a uniform method on both sides of the border. Analyses of entire border regions indicate a slightly higher level of socio-economic development in Czech regions; however, these differences are not significant [58]. Detailed analyses of the entire borderland at the administrative level of municipalities indicate, however, that there are significant local differences in socio-economic development in some border areas [4,5]. In the field of tourism facilities in the Sudetes, the better development on the Czech side is noticeable [59]. To demonstrate the symmetry/asymmetry of the spatial phenomena at the Polish–Czech border, previous studies used cross-sections of administrative units in their analyses [5]. In many cases, analyses of asymmetry in the development of service facilities required direct inventory surveys in border areas [26,29]. However, these surveys were usually based on the point signatures of the studied events on maps and analyses of their overall structures. For linear infrastructure (e.g., roads, transport services, and tourist routes), simplified network analysis methods have been used [54,60]. Square samples, however, are rarely used in research on borderlands, such as in studies of land cover at the Czech–Austrian frontier [15]. As the presented review of literature indicates, detailed spatial and comparative analyses on the development of tourism facilities at the Polish–Czech border remain relatively rare, especially those using geometric grids. By investigating the development of tourism infrastructure in the Orlickie (Orlické) and Bystrzyckie Mountain sub-region of the Sudetes, we fill this gap in the literature.

3. Materials and Methods

3.1. Study Area

For the case study, we chose the border tourist region of the Orlickie Mountains (Orlické hory; Góry Orlickie) and Bystrzyckie Mountains (Góry Bystrzyckie); the physiographic regions that do not overlap with administrative boundaries. This area is located on the Polish–Czech border (Figure 1) in the Sudetes (Sudety Mountains), which is often analyzed in the context of land management or tourism development in its border areas [5,36,61,62,63]. The Sudetes are post-industrial and post-mining region where the role of the service sector, including tourism, is currently growing [25,64,65]. After World War II, these areas were subject to adverse socio-economic phenomena associated with their peripheral location and restrictions related to the political and military protection of the state border between Czechoslovakia and Poland. As a result, depopulation was observed in the Polish borderland, leading to the disappearance of former villages and a decrease in the quality of infrastructure [19,25,66], alongside re-naturalization and an increase in the area of forests [67,68]. The Orlickie and Bystrzyckie Mountains have rarely been the subject of separate studies on the Polish–Czech border, except for the articles of Kołodziejczyk, which analyze the development of marked tourist trail networks [6,60].

3.2. Square Grid

Many spatial analyses are performed by measuring phenomena in specific research fields. In geographical studies, these fields are usually grouped into natural and artificial ones [69]. Natural fields are created based on natural boundaries, while artificial fields can be defined by geometric, administrative, or geodetic divisions. In practice, sharp boundaries (such as the shore of a lake) rarely occur in nature. More often, changes in the environment are gradual, which is why studies establish artificial boundaries for research purposes.

Research fields based on administrative or statistical divisions are convenient due to the availability of public statistical data. These fields are often used in Polish–Czech border studies [5,63]. However, the diversity of their area size and the irregularity of their borders can be problematic in smaller areas. In many studies based on an analysis of administrative units, there is a clear disproportion between large-scale Polish municipalities and clearly smaller Czech ones [5]. In borderland studies, it is possible to use European Union NUTS statistical units [29,63,70], but the mandatory NUTS-3 level for EU member states covers units that are too large for our sub-regional analysis.

Geometric fields are very useful in some studies and are often used because of their uniformity [71]. They constitute an automatically generated, regular grid of research fields of a certain size covering the analyzed area. These methods are particularly suitable to analyze areas that do not have separate statistical, administrative, or geodetic units. They are also often used when presenting phenomena independent of administrative boundaries, particularly in ecology [72] or for presenting statistical data across political boundaries, such as the population grid in the GeoSTAT initiative [73,74]. The availability of analytical computer software has increased the number of socio-economic analyses using this type of method, including research on urban sprawl, land cover [15,75], disease spread [12,13], and space–time accessibility in urban areas [16,76].

The shape chosen for a geometric figure of primary artificial fields (e.g., a square or a hexagon) depends on the type of analysis performed and is mostly a decision made arbitrarily by the analyst. The advantage of hexagons is that their shape is similar to that of a circle and they have a low perimeter to surface ratio. This enables one to divide the space in the most optimal way [16,71]. The use of hexagons is particularly desirable when performing a neighborhood analysis [77]. Artificial geometrical research fields should not be used in areas with large surfaces (e.g., continents) as there is a large distortion of the spherical surface of the Earth on a flat two-dimensional map [78]. However, they are convenient in small areas. The advantage of using a square grid lies in its simplicity of aggregation. Changing the spatial resolution of the grid only requires joining the minimum four cells into a larger one or dividing them depending on whether the resolution is decreased or increased [72]. Regardless of the selected geometric figure, the main advantage of using artificial geometric reference fields is the comparability of the outcomes of the resulting analyses since the division of space is uniform. This factor facilitates interpretation of the spatial differentiation of the phenomenon’s density. In our paper, we decided to use a square grid.

Adopting an appropriate size and shape for the primary fields is important when using the geometric grid method [79]. Fields that are too small can cause a map to lose readability; fields that are too large, however, may distort the results—i.e., they may suggest the occurrence of a phenomenon in a large area, which may be concentrated in one place only. The shape and size of primary field impact some types of analysis, such as those using correlation coefficients, the Lorenz curve, or the Gini coefficient. This issue is called the “modifiable area unit problem” (MAUP) [80,81], which is a statistical biasing effect caused by samples in a given area being used to represent information such as the density of the area. However, this factor has no impact on a density comparison of the whole studied areas (which is the main aim of our paper) when the geometric grid is clipped to its boundaries. In the literature, mathematical formulas for determining the size of the primary fields are usually not given [82]. Therefore, this size is often adopted arbitrarily via the “expert method” (usually with the area or size expressed as integers in multiples of tens, such as 1, 10, and 100 [15,16]. Some researchers used the optimal grid size selection based on a comparison of the coefficient of determination R² [76,83]. In our paper, we decided to use a three kilometers square grid, which gives a basic square-shaped assessment area of nine square kilometers.

The second issue is to determine the extent of the primary geometric fields in relation to the usually-irregular borders of the study area. Such fields can be established with an excess (fields that often go outside the analyzed area [75]), with an underflow (fields that do not go outside the analyzed area [84]), or according to the course of the study boundary (fields are clipped [85]). In the latter case, when grids are clipped to the study area boundary, the primary fields become irregular at the periphery of the study area, so their actual areas must be calculated to analyze the density of the studied phenomenon [85]. In comparative studies of two adjacent areas, trimming the fields to their borders seems necessary. However, some authors used square sampling with an underflow [15]. In the analysis of non-adjacent areas, grids that exceed the research area are the most common [16,75]. In our paper, we use a square grid clipped to the study area boundaries to facilitate comparative analysis of the density indicators.

Figure 2 presents the study area with a basic administrative division and a square grid. The irregularity of the administrative boundaries and the different areas of municipal (commune) districts in Poland and the Czech Republic clearly limit potential comparative spatial analyses (e.g., on the Polish side, there are only seven administrative units of different sizes). Such high diversity of statistical research units compelled us to select arbitrary square grids for analysis. The undoubted advantages of using grid cells include their ease of use for automatic determination using GIS and to perform analyses.

After building a grid of squares, the locations of the square were obtained (division A–K and 1–18, e.g., B4, C8, and J18), as well as the number of cases in a square (DPS—Dot Per Square) for point type objects or the lengths of linear type objects. Squares on the side of the state border were divided into the Polish part (“PL”) and the Czech part (“CZ”, e.g., B3-PL and B3-CZ). The value of the phenomenon density is presented on the choropleth map by the color intensity of a given square.

3.3. The Type of Analysed Tourism Infrastructure

During our research, we encountered a significant problem with data availability and the need to obtain it manually from many disparate sources. In particular, thematic data on tourism infrastructure were difficult to obtain. Existing online databases of accommodation and catering facilities were often outdated and heterogeneous, making the automatic downloading of data for the analysis impractical. Even the current state of marked tourist routes was difficult to obtain from one source. An additional problem was the different systems of data collection and publishing used in neighboring independent countries. The problem of the relevance and diversity of interfaces among publicly available datasets has been often described in the literature [57,86]. Based on the literature review (see Section 2) and the analysis of available data needed to calculate the indicators, six features were ultimately selected:

• Accommodation facilities (locations of hotels, motels, agritourism facilities, sanatoriums, private guest rooms, apartments, and campsites);
• Gastronomic facilities (locations of bars and restaurants, including restaurants in hotels open to people who are not hotel guests);
• Roads (length in km, paved public roads accessible to motorists);
• Hiking marked trails (length in km);
• Cycle tourist marked trails (length in km);
• Ski lifts (every type, length in km).

An inventory of secondary materials was made when data on the study area was collected. Information from the following online sources was used to collect data such as the number and location of accommodations and gastronomic facilities:

• Visit Duszniki (http://visitduszniki.pl, accessed on 26 May 2019),
• Lasówka in the heart of the Sudetes (http://lasowka.info/, accessed on 27 May 2019);
• Accommodations in the Czech Republic and Slovakia (https://www.ceskoslovensko.cz, accessed on 28 May 2019);
• The official tourism Internet portal of the Parubicko region in the Czech Republic https://www.czechy-wschodnie.info, accessed on 28 May 2019);
• The internet portal “Spalona” (http://www.spalona.com.pl/noclegi.php, accessed on 28 May 2019);
• The internet portal “E-turysta” (https://e-turysta.pl, accessed on 28 May 2019).

The locations of specific accommodations and gastronomic facilities were verified by Google Maps (https://www.google.pl/maps/, accessed on 28 May 2019). The data were also verified using information from the individual websites of the examined objects. The accommodations and gastronomic facilities were analyzed without specifying the number of beds in the given objects because such data were not available. Considering only the numbers of these objects makes data interpretation difficult, but obtaining more accurate information would require time-consuming field studies or telephone surveys. The lengths of the ski lifts are based on data from the following websites: “Zieleniec Ski Arena” (https://www.zieleniec.pl/, accessed on 24 May 2019), “Ski info” (https://www.skiinfo.pl/, accessed on 24 May 2019), and “Na narty” (http://www.nanarty.info/, accessed on 24 May 2019).

Reference data, i.e., data on the locations of roads and buildings, were obtained from Open Street Map sources. These data are free. However, they may contain errors, especially in small areas such as villages and small towns because they are updated voluntarily. The locations of all routes, roads, buildings, lifts, etc. were verified using information placed on electronic maps [https://mapa-turystyczna.pl/gory-bystrzyckie, accessed on 24 March 2019] and analogue (printed) tourist maps of the Bystrzyckie Mountains and the Orlické Mountains from the private company Galileos at a scale of 1:40000 (valid for 2016). All data were imported manually, in line with the principle that their characteristics must meet the requirement of having a uniform definition.

3.4. Methods for Calculating the Component Indicators and Final Synthetic Index

For all analyzed features, the following component indicators were used—I_d (number of objects or the length of linear objects per one square km), which are described in the literature on the subject [87]. The general formula for the indicator is

$$I_d=\frac{Lo}{P}$$

(1)

where L_o is the number characterizing the examined element of the infrastructure (e.g., the number of units of point type facilities, such as accommodations and gastronomic facilities, and the total length of linear objects such as tourist routes, cycle routes, ski lifts, etc.); and P is the surface area of a specific statistical unit (research area).

To summarize the development of the studied areas, a synthetic index based on the Human Development Index (HDI) method was used [88]. This method allows one to assess the variability of a group of features in a set of various variables for one year and is a multi-variable method [89]. This index was proposed by the United Nations for international comparative analyses of social development and is also used in geographical sciences [90]. The index is calculated in two stages. In the first stage, variables are separated into the smaller-the-better (STB) and the larger-the-better (LTB) types. LTB means that a variable with an increase in its numerical value is considered a favorable phenomenon, while variables with low values are unfavorable. In the STB type, the interpretation is reversed. Individual component indicators are calculated, obtaining values from 0 to 1 (0 ≤ P_ij ≤ 1). For and LTB,

$$P_{ij}=\frac{(X_{ij}-\min X_i)}{(\max X_i-\min X_i)},$$

(2)

while for the STB,

$$P_{ij}=\frac{(\max X_i-X_{ji})}{(\max X_i-\min X_i)},$$

(3)

where P_ij—the sub-index of the ith feature (i = 1,2,3...,m) in the jth object (j = 1,2,3...,n); X_ij—the value of the ith variable (i = 1,2,3...,m) in the jth object (j = 1,2,3...,n); max X_i—the maximum value of the ith variable; min X_i—the minimum value of the ith feature.

In our analysis, we focused only on the LTB; hence, only one formula was used for the calculations. In the second stage, the synthetic index is calculated from the component indicators:

$${(H)}_j=\frac{1}{m}{\displaystyle \sum _{i=1}^m{P}_{ij}}$$

(4)

where m is the number of component indicators.

In our research, we consider each component indicator related to tourism infrastructure as equally important because each indicator’s weighting is always subjective. The obtained synthetic index, regardless of the number of examined features, always ranges from 0 (with the minimum values of all component indicators) to 1 (with the maximum values of indicators), which facilitates the interpretation of the new variable. In addition, it is relatively resistant to high asymmetry in the statistical distribution of component indicators (as well as in the spatial concentration of the analyzed phenomena). The main disadvantage of the HDI is its subjectivity in the selection of component variables based on the expert method [91]. The component indicators and synthetic index calculated for the entire studied areas are not sensitive to the MAUP problem.

3.5. Analysis of Spatial Distribution

The analyzed tourism infrastructure facilities represent points features (hotels and gastronomic facilities) and linear features (roads, hiking marked trails, cycle tourist marked trails, and ski lifts). We chose the non-parametric Epanechnikov kernel density estimator (KDE) for the spatial distribution analysis [92]. The notation of KDE is

$$\hat{f}\left(x\right)=\frac{1}{n{h}^d}{\displaystyle \sum }_{i=1}^{n}K\left(\frac{1}{h}\left(x-x_i\right)\right)$$

(5)

where K is the kernel function, h is the bandwidth, n is the number of known points within the bandwidth, and d is the data dimensionality [93]. We use the Kernel Density tool in ESRI ArcGIS software to implement KDE. The input parameters of the function are -x,- y coordinates, geographic features representing a variable, the value of the variable of a given feature, and the radius of the search unit area. KDE is useful for detecting hotspots due to the series of estimations that are made over a grid placed on the entire point pattern [94,95]. One of the advantages of applying the KDE is that this method can present the spatial diversity of points and the linear phenomenon distribution regardless of the adopted reference units.

Additionally, we analyzed the spatial concentration of tourism infrastructure facilities using the Lorenz curve [96] and Gini coefficient [97]. The Lorenz curve (Figure 3) is often used in economics and land use research to describe the inequality or concentration of studied phenomenon [98,99]. The mathematical notations and interpretations of the Lorenz curve are widely available in the literature [96,100,101]. In our analysis, the x-axis records the cumulative proportion of the research unit areas, while the y-axis records the cumulative proportion of the infrastructure facility number or length ranked by the infrastructure density indicator. Both ranges are, therefore, (0,1). In our analysis, the Lorenz curve is a straight line of y = x (a line of perfect/equal distribution) when all units have the same density of facilities in each geometric field. The mathematical formula of the Gini coefficient in a graphical interpretation takes the form G = A/(A + B), where A is the area between the Lorenz curve and the line of perfect/equal distribution, while B is the area under the Lorenz curve [97].

In our analysis, a coefficient value G = 0 indicates the same infrastructure density in each test field, while a value close to 1 indicates a strong concentration. The shape of the curve and the Gini coefficient are sensitive to the number and size of the research units (the MAUP problem [100]), so the data for Poland and the Czech Republic cannot be compared. However, the concentration of different infrastructural facilities in one area can be ranked.

4. Results

4.1. Tourism Infrastructure in the Area of the Research

In this sub-section, we analyze the spatial distribution of tourism infrastructure via the descriptive method based on traditional cartographic materials (Figure 4A–C) and its density in the square grid (Figure 5A–F), as well as by using the hotspot KDE method (Figure 6A–F).

On the Polish side of the study, we found a total of 142 accommodation facilities (mainly year-round) in 13 towns or villages. Most of the accommodation facilities (as much as 68% of all on the Polish side of the studied area) were located in Duszniki Zdrój and its mountain district of Zieleniec, while 15 facilities were located in Lasówka. In other locations, the number of accommodation facilities ranged from 1 to 5. On the Czech side of the study, there were 240 accommodation facilities in 22 locations. The largest concentration of accommodation facilities was observed in Deštné v Orlických horách (51), followed by Čenkovice (39) and Říčky v Orlických horách (23). In other villages, the number of accommodation facilities ranged from 2 to 15 (Figure 4A).

For the analysis of the density of accommodations in the square grids, the highest value of the indicator (eight objects per square kilometer) was observed in the square covering the center of the spa town of Duszniki Zdrój (field C2-PL), where 59 accommodation facilities were located. The second highest value was 5.41 for the D6-PL field on the Polish side. However, this result was due to the small area of the research field (0.37 km²), which included only two objects. The third highest result of the indicator value was 4.22 for the district of Dusznik Zdrój–Zieleniec (field C4-PL), which featured 37 accommodation facilities. Of the 48 designated primary fields of assessment, in almost half (26), the value of the indicator was zero. On the Czech side, the highest value of the indicator was 11 and related to the J13-CZ field located in the area of Lichkov. Other high values of the indicator were found in the villages of Orlické Záhoří (field E6-CZ, indicator value 5.68 with five objects), Deštné v Orlických horách (field B5-CZ, indicator value 4.16, number of objects 33), and Říčky v Orlických horách (field D9-CZ, indicator value 2.33; number of objects 21). The value of the accommodation facility density indicator for the entire area on the Polish side was 0.54 and 0.71 on the Czech side. The hotspot analysis via the KDE method confirms the concentration of accommodation facilities in three main locations: nearby Duszniki Zdrój in Poland and nearby Deštné v Orlických horách and Čenkovice in the Czech Republic (Figure 6A).

Gastronomic (catering) facilities are primarily concentrated in the largest towns and villages and, in many cases, coincide with the occurrence of accommodations. On the Polish side of the analyzed border region, the largest number of gastronomic facilities were located in Duszniki Zdrój (16) and Zieleniec (22). Usually, only one facility is located in other locations (the maximum was two). There was a total of 79 gastronomic facilities on the Czech study area. We found the largest number of gastronomic facilities in Deštné v Orlických horách (25), while in the other towns, the number of such facilities was usually three or four. In the designated research fields (Figure 5B), the highest values of the component indicator in the Polish area were 2.51 (22 objects, C4-PL field, Zieleniec) and 2.19 (16 objects, C2-PL field, Duszniki Zdrój). The third area with a high-density indicator (1.72) was the field H13-PL. However, this field contained only one gastronomic object; its high indicator value resulted from the small research area (0.58 km²). The indicator values for other fields did not exceed 0.25, and in 38 fields (out of 48 designated), the indicator value was zero.

On the Czech side, the highest value of the gastronomic facility density was 5.55 (field J13-CZ), but this represented only one object in a field with a small area—0.18 km². Both the B6-CZ field (12 objects, value 2.10) and the B5-CZ field (11 objects, value 1.39) presented lower values of the indicator, both covering fragments of the village Deštné v Orlických horách. On the other fields, the density indicator values did not exceed 1.25, while in 38 fields (out of 67), the indicator was zero. The value of the gastronomic facility density indicator calculated for the entire analyzed area on the Polish side of the study was 0.18, and for the Czech one, this value was 0.22. The hotspot analysis using the KDE method confirmed only two main concentrations of gastronomic facilities: nearby Duszniki Zdrój in Poland and nearby Deštné v Orlických horách in Czech Republic (Figure 6B).

In the Polish area of the study, the total length of paved public roads accessible to motorists was 219.2 km, with 405.0 km available in the Czech area (Figure 4B). The highest road density was recorded in the towns of Duszniki Zdrój (Poland), Deštné v Orlických horách (Czech Republic), and Těchonín (Czech Republic). On the Polish side, the highest road density indicator was 4.27 and belonged to the D6-PL field (Figure 5C); however, its area was only 0.37 km². The lowest value of the indicator belonged to the G4-PL field and amounted to 0.01. Only in five fields of the grid were there no public roads. In the Czech area, the highest value of the indicator was 12.58 and was related to the F13-CZ field; however, the area of this field was only 0.12 km² (1.51 km of roads). The second highest value was 4.63 for the K15-CZ field (road length 0.37 km and field area 0.08 km²). In the Czech Republic, there were no open public roads in the six fields of the grid. The value of the road density component indicator for the Polish area of the study was 0.83 and 1.14 for the Czech area. The KDE method shows the main concentration of road networks in the southern part of the study area in the Czech Republic and in the neighborhoods of Deštné v Orlických horách (Figure 6C)

The total length of hiking trails in the Polish area was 262.5 km and 450.7 km in the Czech area (Figure 4B). The highest density of trails on the Polish side of the study area can be observed in the north nearby Duszniki Zdrój and Polanica Zdrój (Figure 5D). In the Czech area, the highest indicator values were observed in the north-western part of the mountains (e.g., around Deštné v Orlických horách), as well as in the south nearby the border with Poland (around Lichkov and Těchonín). In the analyzed research fields, the highest density indicator value was 8.75 in the A3-PL field; however, the area of this field was only 0.12 km², and there were 1.05 km of hiking trails. The second highest value was 3.74 for H13-PL; however, the area of the evaluation field was also low in this case—0.58 km². There were, moreover, no hiking trails in two research fields. In the Czech area, the highest indicator value was 9.26 in the C4-CZ field, but the area of this field was only 0.23 km². The second highest value was 4.82 for the irregular field B8-CZ, with an area of 0.76 km². There were no hiking trails in the eight fields of the basic assessment. The value of the density for hiking trail network in the Polish study area was 0.99 and 1.27 in the Czech area. The KDE method shows a light concentration of marked trails in the north-western area, which was weaker in the southern part of the research area in the Czech Republic (Figure 6D).

The network of marked cycle trails and hiking routes was relatively dense nearby towns such as Duszniki Zdrój in Poland and Výprachtice, Mladkov, and Orličky in the Czech Republic (Figure 4B). The total length of marked cycle trails was 201.5 km in the Polish area and 317.5 km in the Czech one. In the Polish area, the highest value of the density indicator of cycle trails was 2.81 in the D6-PL field (1.04 km of trails) (Figure 5E). There were no cycle trails in seven fields of the primary assessment. In the Czech area, the highest density indicator value was 4.42 in the F13-CZ field, but its area was only 0.12 km². The second highest value was 3.20 for E11-CZ, with an area of 2.13 km² and a trail length of 6.81 km. There were no cycle trails in the nine fields of the basic assessment. The value of the cycle trail density indicator for the Polish area in the study was 0.76 and 0.92 for the Czech area. The KDE method showed a light concentration of marked cycle trails in the southern part of the study area in the Czech Republic and in the northern part of the study area in Poland, nearby Kudowa Zdrój (Figure 6E).

Ski lifts were located only near Zieleniec in the study area in Poland, and their total length was 7.5 km (Figure 4C). They appeared only in two evaluation fields: C4-PL (indicator 0.8) and C5-PL (indicator 0.27) (Figure 5F). In the Czech Republic, these lifts were located in several places; their total length was 14.7 km, and they appeared in nine evaluation fields. The highest value of the indicator (0.86) was found for the B6-CZ irregular field of 5.71 km², located in Deštné v Orlických horách. The value of the density ratio of ski lifts in the Polish study area was 0.03 and 0.04 for the Czech Republic area. The KDE method showed one main hotspot on the Czech/Polish border, as well as two less visible hotspots (Figure 6F).

The analysis of Gini coefficients (

Table 1. Gini coefficients of tourism infrastructure concentration in the Czech and Polish research areas. Note: The coefficients between Poland and the Czech Republic cannot be compared due to differences in the number and area of the research fields clipped to the study area boundaries. Acronyms: HT—Hiking Trails; CT—Cycle Trails; RS—Roads; AF—Accommodation facilities; GF—Gastronomic Facilities; SL—Ski Lifts. Source: author’s own research.

Study Area	HT	CT	RS	AF	GF	SL
Czech Republic	0.29	0.25	0.33	0.67	0.70	0.90
Poland	0.31	0.34	0.42	0.84	0.89	0.96

) and Lorenz curves (Figure 7) confirms the features of the studied infrastructure facility concentrations in both study areas. The most concentrated features on both sides of the border were ski lifts. In Poland, gastronomic facilities were more concentrated than accommodation facilities, when the Czech Republic had similar levels of concentration for both. In both Poland and Czech Republic, the most commonly dispersed facilities were marked hiking and cycle trails, followed by the road network.

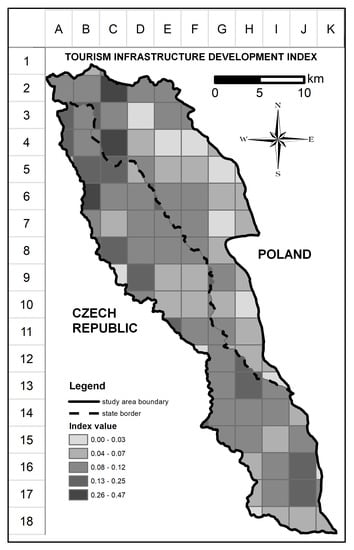
4.2. Synthetic Index of Tourism Infrastructure Development

The density analysis of the studied elements of tourism infrastructure in square research fields enabled us to prepare a summary choropleth map on the development of this infrastructure based on the HDI method (Figure 8).

The highest index values in the Polish study area were obtained by fields covering Duszniki Zdrój and its district, Zieleniec (fields C2-PL and C4-PL). These were the most developed areas in terms of the density of their accommodations and gastronomic facilities, as well as their marked tourist trails. In the Czech area, the best developed tourism infrastructure was located around Deštné v Orlických horách (field B6-CZ), followed by the south of the study area around Orličky (field J16-CZ), Čenkovice (field J17-CZ) and Výprachtice (field I16-CZ, I17-CZ), in the central parts nearby the Polish border—Mladkov (field H13-CZ), České Petrovice (field H12-CZ), Říčky v Orlických horách (field D9-CZ), and Zdobnice (field C8-CZ). The value of the synthetic index of tourism infrastructure development in the Polish area was 0.082 compared to 0.106 in the Czech area. Thus, the index ratio in the Czech area is generally 1.29 higher than that in the Polish area. Such a comparison is not possible with the KDE method.

5. Discussion

In this paper, to assess the asymmetry of tourism infrastructure development in Polish and Czech border areas, we performed an analysis using two basic methods—considering tourism infrastructure density indicators in square fields and examining hotspots using the KDE method. We additionally used the HDI index, which made it possible to carry out a synthetic analysis considering all analyzed component indicators and the Lorenz curve with the Gini coefficient to analyze the spatial concentration of the infrastructure. The HDI synthetic index of tourism infrastructure density enabled the quantitative assessment of differences in tourism infrastructure development in the Polish and Czech areas of the researched region, considering both point and linear types of infrastructure. This confirmed the asymmetry in the development of the analyzed area, which was almost 30% higher on the Czech side than on the Polish side. This confirms the results of other authors’ research on the Sudetes using other methods [5,59]. The existing diversity is the result of historical and political conditions. Czechoslovakia (and then the Czech Republic) has existed in the area since the end of World War I (except 1938–1945). However, the areas of the Sudetes were given to Poland only in 1945 as a result of the political decisions of the anti-Hitler coalition [102]. Former German residents were forcibly displaced after World War II. The significant area of the Polish Sudetes was a special border zone covered by various types of settlement and travel restrictions and was protected by the Border Protection Forces until 1991. This led to strong depopulation processes, a lack of new investments, and the gradual degradation of pre-existing tourism infrastructure [19,55,103]. In the 1980s, these areas had the highest consumption rates of fixed capital in Poland [17,56]. Adverse phenomena, however, occurred in the area until the beginning of the 21st century [104]. The development impulse came as a result of the gradual opening of the state border and the accession of Poland and the Czech Republic in 2004 to the European Union [66]. This was associated with strong support for investments in border areas from European Union aid funds and a rapid development in tourism [62,105]. However, as the research indicates, during these dozen years of development, it has not been possible to eliminate the significant differences between the Polish and Czech portions of the examined border region. Investment in tourism infrastructure is considered an important tool to regenerate marginalized territories [106].

Infrastructure development in the studied areas is heterogeneous and clearly shows a tendency to concentrate around major tourist destinations. The square grid used in this article made it possible to present the spatial diversity of the phenomenon and thereby calculate (and easily interpret) the relevant density indicators. However, these indicators led to a significant generalization of the spatial occurrence of phenomena. The most significant problem was trimming the square fields to the study boundaries and to the state border. At the external boundaries, it was theoretically possible to use full fields with an excess, which has been done in many studies [16,75,107]. However, this was not possible in areas adjacent to the border because, for comparative purposes, cutting off the Czech and Polish parts in the chosen research fields was a necessary condition for analysis. However, this trimming led to the creation of many areas with different surface areas, which partly neglected the benefits of using uniform research fields. The creation of many fields with very small areas was particularly unfavorable. In the comparative borderland research carried out by other authors, a square sample with underflow has also been used, where the squares located on both sides of the border are not adjacent [15]. However, in our case, this would not adequately consider the tourism infrastructures commonly found on the border ridges, which are often important tourist areas [6]. In addition, the analysis of the square fields was burdened by the MAUP problem; indeed, the observed phenomenon would appear slightly different if other square grid sizes were used. Therefore, it was helpful to use additional methods for analyzing the concentration of the infrastructure under study.

The analysis of concentration using the KDE method and Lorenz curve showed that tourism infrastructure is unevenly located in space. Especially on the Polish side, there is a strong concentration in the vicinity of Kudowa Zdrój, while on the Czech side, there are several tourist resorts with two main areas of concentration near Deštné v Orlických horách and Orličky. In the Czech area, this kind of infrastructure is much more dispersed, covering several small towns and villages, which are tourism hot-spots due to their location in attractive mountain areas. KDE analysis showed that downhill skiing infrastructure, accommodations, and gastronomic facilities are characterized by special spatial concentrations in this area. However, the infrastructure for walking, cycling trails, and roads was the most dispersed. This method also clearly showed the locations of clusters of the individual infrastructure facilities that are most often associated with major towns and villages. This method, however, does not enable one to compare the development of entire areas in a synthetic way, which is possible using the HDI method with square fields. In addition, differences in the concentration of the phenomenon are difficult to assess. In this case, the Lorenz curve method and Gini coefficient are helpful, because enable one to clearly determine which elements of development are more or less concentrated in a given area. However, due to the MAUP, it is impossible to compare the concentration of these phenomena in the Polish and Czech areas. The concentration analysis indicates that the unevenness in the development of tourism infrastructure on both sides of the border can be even higher than the results provided by an analysis of the density indicators.

The component indicators concern only a portion of the available infrastructure, the analysis of which can be used for tourism and recreational facility development assessment. It should also be noted that the high density of a given type of infrastructure does not always indicate the development of tourism. The consideration of paved roads is particularly problematic, because housing estates in urban areas with dense street networks, often have nothing to do with tourism. On the other hand, the lack of open public roads can hinder or prevent the development of tourism, as motorized tourists are nowadays of great importance [20].

6. Summary and Conclusions

This study confirmed a higher level of tourism infrastructure in the Czech borderland. The synthetic index of infrastructure development in the studied subregion in the Czech area was 30% higher than that in the Polish one. However, spatial analysis indicates that these differences are locally higher due to the concentration of infrastructure near major tourist centers (towns and villages). The analysis of tourism infrastructure development encounters serious difficulties when accessing standardized data in areas belonging to two separate countries that use different systems for representing, collecting, and publishing data. This paper also shows some possibilities and problems of using the square choropleth map and hotspot KDE method for a comparative spatial analysis of tourist regions. The most important general methodological conclusions are as follows:

(1)

The use of geometric grid cells is particularly beneficial for the analysis and comparison of phenomena occurring in areas that have significantly different sizes of administrative or statistical units or are not internally divided into such units. In this case, data must be obtained from other sources, such as analogue maps, digital maps, satellite images, or field studies (hence, they are often used in ecological research and in cities that form a single administrative unit);

(2)

The advantage of using an artificial geometric grid is its greater readability for the end user compared to a typical choropleth map based on administrative units since the division of space is uniform;

(3)

Full geometric fields facilitate the calculation of density indices that can be used in multivariate analysis, such as HDI, thereby obtaining synthetic measures for the development of the studied phenomenon and considering the component indicators for the linear, point, and surface objects in one index;

(4)

The comparative analysis of features in two adjacent areas using grid methods experiences difficulties associated with the need to irregularly clip (trim) the geometric fields to the boundary of the study area, which is contrary to the principle of dividing the area into equal fields;

(5)

The hotspot KDE method enables one to determine the main clusters of examined infrastructure facilities but does not allow one to create synthetic development indicators for the entire studied area.

Each of the used methods of analysis has its own limitations and strengths. Only the complementary use of several research methods, both methods of spatial statistical analysis (e.g., hotspot) and older methods that are simple but still used in scientific research (e.g., HDI, Lorenz curve, and the Gini coefficient), enables a better understanding of the spatial diversity of the phenomena studied.