Chaotic Quantum Double Delta Swarm Algorithm Using Chebyshev Maps: Theoretical Foundations, Performance Analyses and Convergence Issues
Abstract
:1. Introduction
2. Background
2.1. The Classical PSO
2.2. The Quantum-Behaved PSO
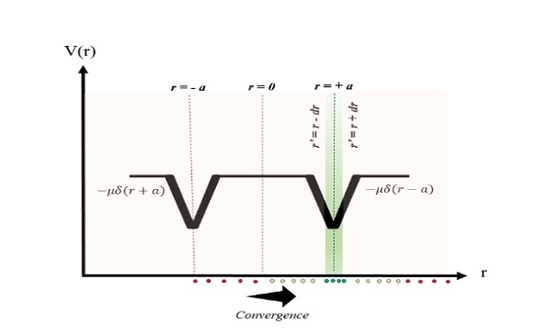
3. Swarming under the Influence of Two Delta Potential Wells
4. The Quantum Double Delta Swarm (QDDS) Algorithm
4.1. QDDS with Chaotic Chebyshev Map (C-QDDS)
4.1.1. Chebyshev Map Driven Solution Update-Motivation
| Algorithm 1. Quantum Double Delta Swarm Algorithm |
 |
4.1.2. Pseudocode of the C-QDDS Algorithm
5. Experimental Setup
5.1. Benchmark Functions
5.2. Parameter Settings
6. Experimental Results
Test Results on Optimization Problems
7. Analysis of Experimental Results
8. Notes on Convergence of the Algorithm
| Algorithm 2. A conditioned approach to solving [5] |
| 1: Initialize x0 in S and set e = 0 |
| 2: Generate ξe from the sample space () |
| 3: Update xe+1 = £ (xe, ξe), choose , set e = e + 1 and repeat Step 1. |
Notes on Theoretical Convergence of the QDDS Algorithm
9. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sengupta, S.; Basak, S.; Peters, R.A. QDDS: A Novel Quantum Swarm Algorithm Inspired by a Double Dirac Delta Potential. Proceedings of 2018 IEEE Symposium Series on Computational Intelligence. arXiv, 2018; arXiv:1807.02870.in press. [Google Scholar]
- Sun, J.; Feng, B.; Xu, W.B. Particle swarm optimization with particles having quantum behavior. In Proceedings of the IEEE Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; pp. 325–331. [Google Scholar]
- Sun, J.; Xu, W.B.; Feng, B. A global search strategy of quantum behaved particle swarm optimization. In Proceedings of the 2004 IEEE Conference on Cybernetics and Intelligent Systems, Singapore, 1–3 December 2004; pp. 111–116. [Google Scholar]
- Xi, M.; Sun, J.; Xu, W. An improved quantum-behaved particle swarm optimization algorithm with weighted mean best position. Appl. Math. Comput. 2008, 205, 751–759. [Google Scholar] [CrossRef]
- Solis, F.J.; Wets, R.J.-B. Minimization by random search techniques. Math. Oper. Res. 1981, 6, 19–30. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Network, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm: Explosion, stability, and convergence in a multi-dimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Peters, R.A., II. Particle Swarm Optimization: A Survey of Historical and Recent Developments with Hybridization Perspectives. Mach. Learn. Knowl. Extr. 2018, 1, 157–191. [Google Scholar] [CrossRef]
- Khare, A.; Rangnekar, S. A review of particle swarm optimization and its applications in Solar Photovoltaic system. Appl. Soft Comput. 2013, 13, 2997–3006. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A Comprehensive Review of Swarm Optimization Algorithms. PLoS ONE 2015, 10, e0122827. [Google Scholar] [CrossRef]
- Xi, M.; Wu, X.; Sheng, X.; Sun, J.; Xu, W. Improved quantum-behaved particle swarm optimization with local search strategy. J. Algorithms Comput. Technol. 2017, 11, 3–12. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S. Computationally efficient low-pass FIR filter design using Cuckoo Search with adaptive Levy step size. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016; pp. 324–329. [Google Scholar]
- Dhabal, S.; Sengupta, S. Efficient design of high pass FIR filter using quantum-behaved particle swarm optimization with weighted mean best position. In Proceedings of the 2015 Third International Conference on Computer, Communication, Control and Information Technology (C3IT), Hooghly, India, 7–8 February 2015; pp. 1–6. [Google Scholar]
- Griffiths, D.J. Introduction to Quantum Mechanics, 2nd ed.; Problem 2.27; Pearson Education: London, UK, 2005. [Google Scholar]
- Basak, S. Lecture Notes, P303 (PE03) Quantum Mechanics I, National Institute of Science Education and Research, India. Available online: http://www.niser.ac.in/~sbasak/p303_2010/06.09.pdf (accessed on 10 March 2018).
- Tatsumi, K.; Tetsuzo, T. A perturbation based chaotic system exploiting the quasi-newton method for global optimization. Int. J. Bifur. Chaos 2017, 27, 1750047. [Google Scholar] [CrossRef]
- He, D.; He, C.; Jiang, L.; Zhu, H.; Hu, G. Chaotic characteristic of a one-dimensional iterative map with infinite collapses. IEEE Trans. Circuits Syst. 2001, 48, 900–906. [Google Scholar]
- Coelho, L.; Mariani, V.C. Use of chaotic sequences in a biologically inspired algorithm for engineering design optimization. Expert Syst. Appl. 2008, 34, 1905–1913. [Google Scholar] [CrossRef]
- Gandomi, A.; Yang, X.-S.; Talatahari, S.; Alavi, A. Firefly algorithm with chaos. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 89–98. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.; Gandomi, A.H.; Hao, G.-S.; Wang, H. Chaotic krill herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 24, 1053–1073. [Google Scholar] [CrossRef]
- Mirjalili, S. The ant lion optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithms for multimodal optimization. In Stochastic Algorithms: Foundations and Applications, SAGA 2009; Lecture Notes in Computer Sciences; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5792, pp. 169–178. [Google Scholar]
- Xie, Z.; Liu, Q.; Xu, L. A New Quantum-Behaved PSO: Based on Double δ-Potential Wells Model. In Proceedings of the 2016 Chinese Intelligent Systems Conference, CISC 2016, Xiamen, China, 22–23 October 2016; Lecture Notes in Electrical Engineering. Springer: Singapore, 2016; Volume 404, pp. 211–219. [Google Scholar]
- Han, P.; Yuan, S.; Wang, D. Thermal System Identification Based on Double Quantum Particle Swarm Optimization. In Proceedings of the Intelligent Computing in Smart Grid and Electrical Vehicles, ICSEE 2014, LSMS 2014, Communications in Computer and Information Science, Shanghai, China, 20–23 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; Volume 463, pp. 125–137. [Google Scholar]
- Jia, P.; Duan, S.; Yan, J. An enhanced quantum-behaved particle swarm optimization based on a novel computing way of local attractor. Information 2015, 6, 633–649. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A. A convergence proof for the particle swarm optimiser. Fundam. Inf. 2010, 105, 341–374. [Google Scholar]
- Fang, W.; Sun, J.; Chen, H.; Wu, X. A decentralized quantuminspired particle swarm optimization algorithm with cellular structured population. Inf. Sci. 2016, 330, 19–48. [Google Scholar] [CrossRef]
- Gao, Y.; Du, W.; Yan, G. Selectively-informed particle swarm optimization. Sci. Rep. 2015, 5, 9295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, C.; Du, W.B.; Wang, W.X. Particle Swarm Optimization with Scale-Free Interactions. PLoS ONE 2014, 9, e97822. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, S.; Basak, S.; Peters, R.A. Data Clustering using a Hybrid of Fuzzy C-Means and Quantum-behaved Particle Swarm Optimization. In Proceedings of the 2018 IEEE 8th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 8–10 January 2018; pp. 137–142. [Google Scholar]




| Term | Discussion |
|---|---|
| Some General Terms | |
| Population (X) | The collection or ‘swarm’ of agents employed in the search space |
| Fitness Function (f) | A measure of convergence efficiency |
| Current Iteration | The ongoing iteration among a batch of dependent/independent runs |
| Maximum Iteration Count | The maximum number of times runs are to be performed |
| Particle Swarm Optimization (PSO) | |
| Position (X) | Position value of individual swarm member in multidimensional space |
| Velocity (v) | Velocity values of individual swarm members |
| Cognitive Accl. Coefficient (C1) | Empirically found scale factor of pBest attractor |
| Social Accl. Coefficient (C2) | Empirically found scale factor of gBest attractor |
| Personal Best (pBest) | Position corresponding to historically best fitness for a swarm member |
| Global Best (gBest) | Position corresponding to best fitness over history for swarm members |
| Inertia Weight Coefficient (ω) | Facilitates and modulates exploration in the search space |
| Cognitive Random Perturbation (r1) | Random noise injector in the Personal Best attractor |
| Social Random Perturbation (r2) | Random noise injector in the Global Best attractor |
| Quantum-behaved Particle Swarm Optimization (QPSO) | |
| Local Attractor | Set of local attractors in all dimensions |
| Characteristic Length | Measure of scales on which significant variations occur |
| Contraction–Expansion Parameter (β) | Scale factor influencing the convergence speed of QPSO |
| Mean Best | Mean of personal bests across all particles, akin to leader election in species |
| Quantum Double–Delta Swarm Optimization (QDDS) | |
| Component towards the global best position gbest | |
| Wave function in the Schrodinger’s equation | |
| Even solutions to Schrodinger’s Equation for Double Delta Potential Well | |
| Potential Function | |
| Limiter | |
| Characteristic Constraint | |
| A small fraction between 0 and 1 chosen at will | |
| Region 1 | |
| Region 2 | |
| Region 3 | |
| Learning Rate | |
| Component towards global best gbest drawn from Chebyshev map | |
| Depth of the wells | |
| Coordinate of wells | |
| Number | Name | Expression | Range | Min |
|---|---|---|---|---|
| F1 | Sphere | [−100, 100] | f(x*) = 0 | |
| F2 | Schwefel’s Problem 2.22 | [−10, 10] | f(x*) = 0 | |
| F3 | Schwefel’s Problem 1.2 | [−100, 100] | f(x*) = 0 | |
| F4 | Schwefel’s Problem 2.21 | [−100, 100] | f(x*) = 0 | |
| F5 | Generalized Rosenbrock’s Function | [−n, n] | f(x*) = 0 | |
| F6 | Step Function | [−100, 100] | f(x*) = 0 | |
| F7 | Quartic Function i.e., Noise | [−1.28, 1.28] | f(x*) = 0 |
| Number | Name | Expression | Range | Min |
|---|---|---|---|---|
| F8 | Generalized Schwefel’s Problem 2.26 | [−500, 500] | f(x*) = −12,569.5 | |
| F9 | Generalized Rastrigrin’s Function | , A = 10 | [−5.12, 5.12] | f(x*) = 0 |
| F10 | Ackley’s Function | [−32.768, 32.768] | f(x*) = 0 | |
| F11 | Generalized Griewank Function | [−600, 600] | f(x*) = 0 | |
| F12 | Generalized Penalized Function 1 | [−50, 50] | f(x*) = 0 | |
| F13 | Generalized Penalized Function 2 | where | [−50, 50] | f(x*) = 0 |
| Number | Name | Expression | Range | Min |
|---|---|---|---|---|
| F14, n = 2 | Shekel’s Foxholes Function | where | [−65.536, 65.536] | f(x*) ≈ 1 |
| F15, n = 4 | Kowalik’s Function | Coefficients are defined according to Table F15. | [−5, 5] | f(x*) ≈ 0.0003075 |
| F16, n = 2 | Six-Hump Camel-Back Function | [−5, 5] | f(x*) = −1.0316285 | |
| F17, n = 2 | Branin Function | , | f(x*) = 0.398 | |
| F18, n = 2 | Goldstein-Price Function | [−2, 2] | f(x*) = 3 | |
| F19, n = 3 | Hartman’s Family Function 1 | f(x*) = −3.86 | ||
| F20, n = 6 | Hartman’s Family Function 2 | Coefficients are defined according to Table F20.1 and F20.2 respectively. | f(x*) = −3.86 | |
| F21, n = 4 | Shekel’s Family Function 1 | Coefficients are defined according to Table F21. | ||
| F22, n = 4 | Shekel’s Family Function 2 | Coefficients are defined according to Table F22. | ||
| F23, n = 4 | Shekel’s Family Function 3 | Coefficients are defined according to Table F23. |
| Index (i) | ||
|---|---|---|
| 1 | 0.1957 | 0.25 |
| 2 | 0.1947 | 0.5 |
| 3 | 0.1735 | 1 |
| 4 | 0.1600 | 2 |
| 5 | 0.0844 | 4 |
| 6 | 0.0627 | 6 |
| 7 | 0.0456 | 8 |
| 8 | 0.0342 | 10 |
| 9 | 0.0323 | 12 |
| 10 | 0.0235 | 14 |
| 11 | 0.0246 | 16 |
| Index (i) | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 3 | 10 | 30 | 1 | 0.3689 | 0.1170 | 0.2673 |
| 2 | 0.1 | 10 | 35 | 1.2 | 0.4699 | 0.4387 | 0.7470 |
| 3 | 3 | 10 | 30 | 3 | 0.1091 | 0.8732 | 0.5547 |
| 4 | 0.1 | 10 | 35 | 3.2 | 0.038150 | 0.5743 | 0.8828 |
| Index (i) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 3 | 17 | 3.5 | 1.7 | 8 | 1 | 0.1312 | 0.1696 | 0.5569 | 0.0124 | 0.8283 | 0.5886 |
| 2 | 0.5 | 10 | 17 | 0.1 | 8 | 14 | 1.2 | 0.2329 | 0.4135 | 0.8307 | 0.3736 | 0.1004 | 0.9991 |
| 3 | 3 | 3.5 | 1.7 | 10 | 17 | 8 | 3 | 0.2348 | 0.1415 | 0.3522 | 0.2883 | 0.3047 | 0.6650 |
| 4 | 17 | 8 | 0.05 | 10 | 0.1 | 14 | 3.2 | 0.4047 | 0.8828 | 0.8732 | 0.5743 | 0.1091 | 0.0381 |
| Index (i) | |||||
|---|---|---|---|---|---|
| 1 | 4 | 4 | 4 | 4 | 0.1 |
| 2 | 1 | 1 | 1 | 1 | 0.2 |
| 3 | 8 | 8 | 8 | 8 | 0.4 |
| 4 | 6 | 6 | 6 | 6 | 0.4 |
| 5 | 3 | 7 | 3 | 7 | 0.4 |
| 6 | 2 | 9 | 2 | 9 | 0.6 |
| 7 | 5 | 5 | 3 | 3 | 0.3 |
| 8 | 8 | 1 | 8 | 1 | 0.7 |
| 9 | 6 | 2 | 6 | 2 | 0.5 |
| 10 | 7 | 3.6 | 7 | 3.6 | 0.5 |

| Fn | Stat | C-QDDS Chebyshev Map | Sine Cosine Algorithm | Dragon Fly Algorithm | Ant Lion Optimization | Whale Optimization | Firefly Algorithm | QPSO | PSO w = 0.95*w | PSO No Damping |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 1.1956 × 10−6 | 0.0055 | 469.8818 | 7.8722 × 10−7 | 17.3824 | 3.5794 × 104 | 3.0365 × 103 | 109.5486 | 110.3989 |
| Min | 5.1834 × 10−7 | 1.0207 × 10−7 | 23.9914 | 8.9065 × 10−8 | 0.6731 | 3.0236 × 104 | 1.3286 × 103 | 39.3329 | 42.8825 | |
| Std | 2.8711 × 10−7 | 0.0161 | 474.0822 | 1.0286 × 10−6 | 19.6687 | 3.3373 × 103 | 920.4817 | 43.3127 | 54.7791 | |
| F2 | Mean | 0.0051 | 3.6862 × 10−6 | 9.2230 | 27.8542 | 0.7846 | 3.4566 × 104 | 36.4162 | 4.2299 | 4.4102 |
| Min | 0.0025 | 2.7521 × 10−9 | 0 | 0.0029 | 0.0745 | 84.8978 | 21.7082 | 2.0290 | 2.1627 | |
| Std | 9.7281 × 10−4 | 8.9681 × 10−6 | 5.7226 | 42.2856 | 0.5303 | 1.3595 × 105 | 12.5312 | 1.1111 | 1.3804 | |
| F3 | Mean | 1.0265 × 10−4 | 3.4383 × 103 | 6.3065 × 103 | 302.3783 | 1.0734 × 105 | 4.4017 × 104 | 3.0781 × 104 | 4.0409 × 103 | 3.4218 × 103 |
| Min | 1.0184 × 10−5 | 27.3442 | 310.7558 | 102.7732 | 5.0661 × 104 | 3.0021 × 104 | 1.8940 × 104 | 2.2416 × 103 | 1.9223 × 103 | |
| Std | 6.5905 × 10−5 | 3.1641 × 103 | 4.7838 × 103 | 167.7687 | 4.0661 × 104 | 6.6498 × 103 | 5.9848 × 103 | 994.2550 | 997.4284 | |
| F4 | Mean | 3.6945 × 10−4 | 12.8867 | 13.8222 | 8.8157 | 66.4261 | 68.4102 | 56.5926 | 12.8272 | 11.9252 |
| Min | 1.4162 × 10−4 | 1.4477 | 4.1775 | 2.0212 | 17.8904 | 62.9296 | 32.6744 | 10.2302 | 9.0857 | |
| Std | 9.8034 × 10−5 | 8.1625 | 5.5197 | 3.0808 | 21.5187 | 2.6497 | 8.2985 | 1.5793 | 2.0508 | |
| F5 | Mean | 28.7211 | 60.7787 | 2.0123 × 104 | 143.9657 | 1.5976 × 103 | 7.4584 × 107 | 2.1204 × 106 | 6.0590 × 103 | 5.3377 × 103 |
| Min | 28.7074 | 28.0932 | 44.0682 | 20.7989 | 39.9132 | 3.8917 × 107 | 5.0759 × 105 | 655.5618 | 1.2610 × 103 | |
| Std | 0.0077 | 55.2793 | 3.6793 × 104 | 288.1879 | 3.0458 × 103 | 2.0606 × 107 | 9.1390 × 105 | 4.2558 × 103 | 2.6303 × 103 | |
| F6 | Mean | 7.2332 | 4.2963 | 488.3942 | 6.0117 × 10−7 | 30.0158 | 3.6216 × 104 | 3.6028 × 103 | 107.5196 | 116.9431 |
| Min | 6.4389 | 3.3201 | 17.4978 | 8.9390 × 10−8 | 0.8531 | 2.8838 × 104 | 1.8380 × 103 | 45.9374 | 28.9258 | |
| Std | 0.5612 | 0.4007 | 309.2795 | 6.2634 × 10−7 | 44.1595 | 2.8434 × 103 | 986.7972 | 47.5633 | 49.5767 | |
| F7 | Mean | 0.0037 | 0.0289 | 0.1491 | 0.0541 | 0.1265 | 36.0335 | 1.4761 | 0.1737 | 0.1749 |
| Min | 4.9685 × 10−4 | 0.0010 | 0.0157 | 0.0210 | 0.0177 | 21.1334 | 0.3837 | 0.0697 | 0.0734 | |
| Std | 0.0023 | 0.0472 | 0.0918 | 0.0229 | 0.0993 | 7.5632 | 0.7718 | 0.0561 | 0.0690 |
| Fn | Stat | C-QDDS Chebyshev Map | Sine Cosine Algorithm | Dragon Fly Algorithm | Ant Lion Optimizer | Whale Optimization | Firefly Algorithm | QPSO | PSO w = 0.95*w | PSO No Damping |
|---|---|---|---|---|---|---|---|---|---|---|
| F8 | Mean | −602.2041 | −4.0397 × 103 | −6.001 × 103 | −5.5942 × 103 | −8.5061 × 103 | −3.8714 × 103 | −3.3658 × 103 | −5.1487 × 103 | −4.8821 × 103 |
| Best | −975.5422 | −4.4739 × 103 | −8.9104 × 103 | −8.2843 × 103 | −1.0768 × 104 | −4.2603 × 103 | −5.0298 × 103 | −7.4208 × 103 | −6.6643 × 103 | |
| Std | 160.8409 | 214.0523 | 783.7255 | 515.1599 | 895.4642 | 204.0029 | 486.0400 | 766.3330 | 750.3092 | |
| F9 | Mean | 2.4873 × 10−4 | 8.8907 | 124.0432 | 79.9945 | 116.4796 | 328.4011 | 248.0831 | 57.8114 | 57.1125 |
| Best | 8.2194 × 10−5 | 1.0581 × 10−6 | 32.1699 | 45.7681 | 0.4305 | 308.3590 | 177.8681 | 19.1318 | 27.4985 | |
| Std | 6.3770 × 10−5 | 16.2284 | 40.4730 | 22.2932 | 88.0344 | 10.1050 | 31.9501 | 15.1644 | 15.0292 | |
| F10 | Mean | 8.1297 × 10−4 | 10.7873 | 6.0693 | 1.6480 | 1.1419 | 19.3393 | 12.3433 | 4.9951 | 4.9271 |
| Best | 5.6777 × 10−4 | 3.4267 × 10−5 | 8.8818 × 10−16 | 1.7296 × 10−4 | 0.0265 | 18.4515 | 9.7835 | 3.9874 | 2.9208 | |
| Std | 8.8526 × 10−5 | 9.6938 | 1.9141 | 0.9544 | 0.9926 | 0.2797 | 1.8413 | 0.6230 | 0.7957 | |
| F11 | Mean | 8.7473 × 10−8 | 0.1770 | 5.0784 | 0.0082 | 1.1735 | 316.5026 | 33.5446 | 2.0669 | 2.0604 |
| Best | 3.5705 × 10−8 | 2.2966 × 10−5 | 1.1727 | 2.5498 × 10−5 | 0.9839 | 226.5205 | 11.9701 | 1.3636 | 1.3744 | |
| Std | 2.6504 × 10−8 | 0.2195 | 4.5098 | 0.0093 | 0.2340 | 33.3806 | 12.5605 | 0.5989 | 0.5366 | |
| F12 | Mean | 0.0995 | 991.4301 | 12.2571 | 9.4380 | 642.0404 | 1.2629 × 108 | 5.6147 × 105 | 6.4329 | 6.5610 |
| Best | 0 | 0.2878 | 1.6755 | 3.4007 | 0.0442 | 5.6104 × 107 | 4.0841 × 104 | 1.0266 | 2.8742 | |
| Std | 0.2621 | 5.4201 × 103 | 13.5218 | 3.9121 | 3.5039 × 103 | 4.4034 × 107 | 6.9761 × 105 | 2.7882 | 3.0003 | |
| F13 | Mean | 0.0105 | 3.1940 | 1.5156 × 104 | 0.0133 | 2.3405 × 103 | 2.8867 × 108 | 3.5568 × 106 | 38.1945 | 39.0369 |
| Best | 0 | 1.8776 | 5.6609 | 2.7212 × 10−7 | 0.3813 | 1.3101 × 108 | 6.8216 × 105 | 12.7653 | 15.4619 | |
| Std | 0.0576 | 2.2922 | 6.0811 × 104 | 0.0163 | 1.2373 × 104 | 8.1766 × 107 | 2.4393 × 106 | 15.2922 | 27.6751 |
| Fn | Stat | C-QDDS Chebyshev Map | Sine Cosine Algorithm | Dragon Fly Algorithm | Ant Lion Optimizer | Whale Optimization | Firefly Algorithm | QPSO | PSO w = 0.95*w | PSO No Damping |
|---|---|---|---|---|---|---|---|---|---|---|
| F14, n = 2 | Mean | 3.6771 | 1.3949 | 1.0311 | 1.2299 | 4.2524 | 1.0519 | 2.3561 | 2.7786 | 3.7082 |
| Best | 1.0056 | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9980 | 0.9981 | 0.9980 | 0.9980 | |
| Std | 2.2295 | 0.8072 | 0.1815 | 0.4276 | 3.7335 | 0.1889 | 1.7188 | 2.2246 | 2.7536 | |
| F15, n = 4 | Mean | 3.7361 × 10−4 | 9.1075 × 10−4 | 0.0016 | 0.0027 | 0.0051 | 0.0024 | 0.0030 | 0.0036 | 0.0034 |
| Best | 3.1068 × 10−4 | 3.1549 × 10−4 | 4.7829 × 10−4 | 4.0518 × 10−4 | 3.4820 × 10−4 | 0.0011 | 7.2169 × 10−4 | 3.6642 × 10−4 | 3.0858 × 10−4 | |
| Std | 5.0123 × 10−5 | 4.2242 × 10−4 | 0.0014 | 0.0060 | 0.0076 | 0.0012 | 0.0059 | 0.0063 | 0.0068 | |
| F16, n = 2 | Mean | −0.5487 | −1.0316 | −1.0316 | −1.0316 | −1.0315 | −1.0295 | −1.0316 | −1.0316 | −1.0316 |
| Best | −1.0315 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | |
| Std | 0.4275 | 1.1863 × 10−5 | 1.4229 × 10−6 | 3.6950 × 10−14 | 3.3613 × 10−4 | 0.0030 | 1.1009 × 10−4 | 8.2108 | 2.7251 × 10−13 | |
| F17, n = 2 | Mean | 0.4721 | 0.3983 | 0.3979 | 0.3979 | 0.4069 | 0.4002 | 0.4000 | 0.3979 | 0.3979 |
| Best | 0.3989 | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.3979 | |
| Std | 0.0920 | 4.8435 × 10−4 | 4.9327 × 10−8 | 2.3588 × 10−14 | 0.0179 | 0.0020 | 0.0043 | 5.0770 × 10−10 | 2.1067 × 10−8 | |
| F18, n = 2 | Mean | 3.8438 | 3 | 3 | 3 | 3.9278 | 3.0402 | 3.0007 | 3.0000 | 3.0000 |
| Best | 3.0080 | 3 | 3 | 3 | 3.0000 | 3.0002 | 3.0000 | 3.0000 | 3.0000 | |
| Std | 0.9128 | 5.7657 × 10−6 | 8.7817 × 10−7 | 1.2869 × 10−13 | 5.0752 | 0.0397 | 0.0017 | 1.0155 × 10−11 | 5.8511 × 10−11 | |
| F19, n = 3 | Mean | −3.6805 | −3.8547 | −3.8625 | −3.8628 | −3.8246 | −3.8542 | −3.8628 | −3.8628 | −3.8628 |
| Best | −3.8587 | −3.8626 | −3.8628 | −3.8628 | −3.8628 | −3.8625 | −3.8628 | −3.8628 | −3.8628 | |
| Std | 0.1942 | 0.0016 | 8.8455 × 10−4 | 7.5193 × 10−15 | 0.0657 | 0.0066 | 1.5043 × 10−5 | 5.2841 × 10−11 | 9.2140 × 10−11 | |
| F20, n = 6 | Mean | −2.2207 | −2.9961 | −3.2421 | −3.2705 | −3.0966 | −3.0645 | −3.2646 | −3.2625 | −3.2546 |
| Best | −2.7562 | −3.2911 | −3.3220 | −3.3220 | −3.2610 | −3.2436 | −3.3219 | −3.3220 | −3.3220 | |
| Std | 0.29884 | 0.2060 | 0.0670 | 0.0599 | 0.1535 | 0.0911 | 0.0605 | 0.0605 | 0.0599 | |
| F21, n = 4 | Mean | −3.1126 | −4.0962 | −9.0360 | −6.7752 | −6.5291 | −4.3198 | −5.8537 | −5.3955 | −5.4045 |
| Best | −4.5610 | −5.3343 | −10.1532 | −10.1532 | −9.8465 | −7.5958 | −10.1474 | −10.1532 | −10.1532 | |
| Std | 0.7090 | 1.5519 | 1.9130 | 2.6824 | 1.9988 | 1.4599 | 3.5651 | 3.3029 | 3.4897 | |
| F22, n = 4 | Mean | −3.2009 | −3.9949 | −10.0455 | −7.2979 | −6.3611 | −4.2776 | −6.7830 | −5.3236 | −6.3098 |
| Best | −4.5933 | −7.9241 | −10.4029 | −10.4029 | −10.2432 | −9.2741 | −10.3974 | −10.4029 | −10.4029 | |
| Std | 0.7098 | 2.1774 | 1.3422 | 3.0440 | 2.3852 | 1.6527 | 3.5783 | 3.2000 | 3.4602 | |
| F23, n = 4 | Mean | −2.3595 | −4.6650 | −9.9928 | −7.1691 | −5.2592 | −4.6959 | −7.5372 | −7.3175 | −5.1501 |
| Best | −4.2043 | −7.7259 | −10.5364 | −10.5364 | −10.0617 | −8.5734 | −10.5344 | −10.5364 | −10.5364 | |
| Std | 0.8183 | 1.5038 | 1.6439 | 3.2926 | 2.5389 | 1.4647 | 3.6778 | 3.7753 | 3.4033 |
| Performance | Metric | C-QDDS Chebyshev Map | Sine Cosine Algorithm | Dragon Fly Algorithm | Ant Lion Optimizer | Whale Optimization | Firefly Algorithm | QPSO | PSO w = 0.95*w | PSO No Damping |
|---|---|---|---|---|---|---|---|---|---|---|
| Win | Mean | 10 | 1 | 3 | 3 | 1 | 0 | 0 | 0 | 0 |
| Best | 6 | 1 | 2 | 3 | 1 | 0 | 0 | 0 | 1 | |
| Std | 14 | 1 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | |
| Tie | Mean | 0 | 2 | 3 | 4 | 0 | 0 | 2 | 4 | 5 |
| Best | 0 | 4 | 9 | 9 | 5 | 3 | 4 | 9 | 9 | |
| Std | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Lose | Mean | 13 | 20 | 17 | 17 | 22 | 23 | 21 | 19 | 18 |
| Best | 17 | 18 | 12 | 13 | 18 | 20 | 19 | 14 | 13 | |
| Std | 9 | 22 | 22 | 17 | 23 | 23 | 23 | 23 | 23 |
| Performance | Metric | C-QDDS Chebyshev Map | Sine Cosine Algorithm | Dragon Fly Algorithm | Ant Lion Optimizer | Whale Optimization | Firefly Algorithm | QPSO | PSO w = 0.95*w | PSO No Damping |
|---|---|---|---|---|---|---|---|---|---|---|
| Win | Mean | 1 | 3 | 2 | 2 | 3 | 4 | 4 | 4 | 4 |
| Best | 1 | 4 | 3 | 2 | 4 | 5 | 5 | 5 | 4 | |
| Std | 1 | 3 | 3 | 2 | 4 | 4 | 4 | 4 | 4 | |
| Tie | Mean | 5 | 4 | 3 | 2 | 5 | 5 | 4 | 2 | 1 |
| Best | 5 | 3 | 2 | 2 | 3 | 4 | 3 | 2 | 1 | |
| Std | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Lose | Mean | 1 | 5 | 2 | 2 | 7 | 8 | 6 | 4 | 3 |
| Best | 4 | 5 | 1 | 2 | 5 | 7 | 6 | 3 | 2 | |
| Std | 1 | 3 | 3 | 2 | 4 | 4 | 4 | 4 | 3 | |
| Average Rank | Mean | 2.333 | 4 | 2.333 | 2 | 5 | 5.666 | 4.666 | 3.333 | 2.666 |
| Best | 3.333 | 4 | 2 | 2 | 4 | 5.333 | 4.666 | 3.333 | 2.333 | |
| Std | 1 | 2.333 | 2.333 | 1.666 | 3 | 3 | 3 | 3 | 2.666 |
| Algorithm | C-QDDS vs. SCA | C-QDDS vs. DFA | C-QDDS vs. ALO | C-QDDS vs. WOA | C-QDDS vs. FA | C-QDDS vs. QPSO | C-QDDS vs. PSO-II | C-QDDS vs. PSO-I |
|---|---|---|---|---|---|---|---|---|
| Function | t values (tcritical = 2.001717). Null Hypothesis: (µ_CQDDS − µ_Competitor) > 0 | |||||||
| F1 | −1.8707 | −5.4287 | 2.094532 | −4.84055 | −5.8.7456 | −18.0684 | −13.8533 | −11.0385 |
| F2 | 28.69263 | −8.82265 | −3.60728 | −8.05108 | −1.39261 | −15.9148 | −20.8264 | −17.4788 |
| F3 | −5.95188 | −7.22065 | −9.87189 | −14.4592 | −36.2554 | −28.1704 | −22.2608 | −18.7903 |
| F4 | −8.64702 | −13.7155 | −15.6724 | −16.9076 | −141.411 | −37.3523 | −44.4852 | −31.8485 |
| F5 | −3.17636 | −2.99135 | −2.19031 | −2.8213 | −19.825 | −12.7079 | −7.76098 | −11.0552 |
| F6 | 23.32769 | −8.52117 | 70.59491 | −2.82556 | −69.7487 | −19.9572 | −11.5478 | −12.12 |
| F7 | −2.92082 | −8.67254 | −11.9943 | −6.77163 | −26.0926 | −10.4491 | −16.5837 | −13.5823 |
| F8 | 70.32003 | 36.96027 | 50.66345 | 47.58374 | 68.92735 | 29.56635 | 31.80233 | 30.54904 |
| F9 | −3.0006 | −16.7868 | −19.6538 | −7.24698 | −178.004 | −42.529 | −20.8808 | −20.8139 |
| F10 | −6.09462 | −17.3651 | −9.45308 | −6.29659 | −378.696 | −36.7146 | −43.9082 | −33.9102 |
| F11 | −4.41671 | −6.1678 | −4.82933 | −27.4681 | −5.1.933 | −14.6277 | −18.9028 | −21.0311 |
| F12 | −1.00178 | −4.92371 | −13.0453 | −1.00347 | −15.7087 | −4.40833 | −12.3869 | −11.7511 |
| F13 | −7.60459 | −1.36509 | −0.25619 | −1.03608 | −19.337 | −7.98647 | −13.6763 | −7.72376 |
| F14 | 5.271808 | 6.47901 | 5.904436 | −0.72462 | 6.426319 | 2.570191 | 1.562548 | −0.04808 |
| F15 | −6.9162 | −4.79494 | −2.12362 | −3.40618 | −9.2411 | −2.4381 | −2.80494 | −2.43761 |
| F16 | 6.187023 | 6.187023 | 6.187023 | 6.18574 | 6.159965 | 6.187023 | 6.187023 | 6.187023 |
| F17 | 4.393627 | 4.417501 | 4.417501 | 3.810236 | 4.27956 | 4.287797 | 4.417501 | 4.417501 |
| F18 | 5.063193 | 5.063193 | 5.063193 | −0.08922 | 4.81742 | 5.058984 | 5.063193 | 5.063193 |
| F19 | 4.912978 | 5.133083 | 5.141597 | 3.849854 | 4.896216 | 5.141597 | 5.141597 | 5.141597 |
| F20 | 11.70106 | 18.26704 | 18.86578 | 14.28008 | 14.7933 | 18.75247 | 18.71474 | 18.58005 |
| F21 | 3.157566 | 15.90258 | 7.230404 | 8.823441 | 4.074111 | 4.13039 | 3.701433 | 3.525209 |
| F22 | 1.898948 | 24.69127 | 7.179345 | 6.955444 | 3.278706 | 5.378252 | 3.547072 | 4.820763 |
| F23 | 7.375911 | 22.76815 | 7.76455 | 5.953976 | 7.627314 | 7.526917 | 7.029854 | 4.366702 |
| Significantly better | 9 | 12 | 10 | 11 | 12 | 13 | 13 | 13 |
| Significantly worse | 11 | 10 | 12 | 8 | 10 | 10 | 9 | 9 |
| Algorithm | C-QDDS vs. SCA | C-QDDS vs. DFA | C-QDDS vs. ALO | C-QDDS vs. WOA | C-QDDS vs. FA | C-QDDS vs. QPSO | C-QDDS vs. PSO-II | C-QDDS vs. PSO-I |
|---|---|---|---|---|---|---|---|---|
| Function | Cohen’s d-values, where d = | |||||||
| F1 | −0.483 | −1.4017 | 0.5408 | −1.2498 | −15.1681 | −4.6652 | −3.5769 | −2.8501 |
| F2 | 7.4084 | −2.278 | −0.9314 | −2.0788 | −0.3596 | −4.1092 | −5.3773 | −4.513 |
| F3 | −1.5368 | −1.8644 | −2.5489 | −3.7333 | −9.3611 | −7.2736 | −5.7477 | −4.8516 |
| F4 | −2.2327 | −3.5413 | −4.0466 | −4.3655 | −36.5121 | −9.6443 | −11.486 | −8.2233 |
| F5 | −0.8201 | −0.7724 | −0.5655 | −0.7285 | −5.1188 | −3.2812 | −2.0039 | −2.8544 |
| F6 | 6.0232 | −2.2002 | 18.2275 | −0.7296 | −18.009 | −5.1529 | −2.9816 | −3.1294 |
| F7 | −0.7542 | −2.2392 | −3.0969 | −1.7484 | −6.7371 | −2.698 | −4.2819 | −3.5069 |
| F8 | 18.1566 | 9.5431 | 13.0812 | 12.2861 | 17.797 | 7.634 | 8.2113 | 7.8877 |
| F9 | −0.7748 | −4.3343 | −5.0746 | −1.8712 | −45.9603 | −10.9809 | −5.3914 | −5.3741 |
| F10 | −1.5736 | −4.4836 | −2.4408 | −1.6258 | −97.7789 | −9.4797 | −11.3371 | −8.7556 |
| F11 | −1.1404 | −1.5925 | −1.2469 | −7.0922 | −13.4091 | −3.7769 | −4.8807 | −5.4302 |
| F12 | −0.2587 | −1.2713 | −3.3683 | −0.2591 | −4.056 | −1.1382 | −3.1983 | −3.0341 |
| F13 | −1.9635 | −0.3525 | −0.0661 | −0.2675 | −4.9928 | −2.0621 | −3.5312 | −1.9943 |
| F14 | 1.3612 | 1.6729 | 1.5245 | −0.1871 | 1.6593 | 0.6636 | 0.4034 | −0.0124 |
| F15 | −1.7858 | −1.238 | −0.5483 | −0.8795 | −2.386 | −0.6295 | −0.7242 | −0.6294 |
| F16 | 1.5975 | 1.5975 | 1.5975 | 1.5972 | 1.5905 | 1.5975 | 1.5975 | 1.5975 |
| F17 | 1.1344 | 1.1406 | 1.1406 | 0.9838 | 1.105 | 1.1071 | 1.1406 | 1.1406 |
| F18 | 1.3073 | 1.3073 | 1.3073 | −0.023 | 1.2439 | 1.3062 | 1.3073 | 1.3073 |
| F19 | 1.2685 | 1.3254 | 1.3276 | 0.994 | 1.2642 | 1.3276 | 1.3276 | 1.3276 |
| F20 | 3.0212 | 4.7165 | 4.8711 | 3.6871 | 3.8196 | 4.8419 | 4.8321 | 4.7973 |
| F21 | 0.8153 | 4.106 | 1.8669 | 2.2782 | 1.0519 | 1.0665 | 0.9557 | 0.9102 |
| F22 | 0.4903 | 6.3753 | 1.8537 | 1.7959 | 0.8466 | 1.3887 | 0.9158 | 1.2447 |
| F23 | 1.9045 | 5.8787 | 2.0048 | 1.5373 | 1.9694 | 1.9434 | 1.8151 | 1.1275 |
| Algorithm | C-QDDS vs. SCA | C-QDDS vs. DFA | C-QDDS vs. ALO | C-QDDS vs. WOA | C-QDDS vs. FA | C-QDDS vs. QPSO | C-QDDS vs. PSO-II | C-QDDS vs. PSO-I |
|---|---|---|---|---|---|---|---|---|
| Function | Hedge’s g-values, where g = | |||||||
| F1 | −0.6716 | −1.949 | 0.752 | −1.7378 | −21.0904 | −6.4867 | −4.9735 | −3.9629 |
| F2 | 10.301 | −3.1674 | −1.2951 | −2.8905 | −0.5 | −5.7136 | −7.4768 | −6.2751 |
| F3 | −2.1368 | −2.5923 | −3.5441 | −5.1909 | −13.0161 | −10.1135 | −7.9919 | −6.7459 |
| F4 | −3.1044 | −4.924 | −5.6266 | −6.07 | −5.0.768 | −13.4099 | −15.9706 | −11.434 |
| F5 | −1.1403 | −1.074 | −0.7863 | −1.0129 | −7.1174 | −4.5623 | −2.7863 | −3.9689 |
| F6 | 8.3749 | −3.0593 | 25.3443 | −1.0145 | −25.0405 | −7.1648 | −4.1457 | −4.3513 |
| F7 | −1.0487 | −3.1135 | −4.3061 | −2.4311 | −9.3676 | −3.7514 | −5.9537 | −4.8761 |
| F8 | 25.2457 | 13.2691 | 18.1887 | 17.0831 | 24.7457 | 10.6146 | 11.4173 | 10.9674 |
| F9 | −1.0773 | −6.0266 | −7.0559 | −2.6018 | −63.9052 | −15.2683 | −7.4964 | −7.4724 |
| F10 | −2.188 | −6.2342 | −3.3938 | −2.2606 | −135.956 | −13.181 | −15.7636 | −12.1742 |
| F11 | −1.5857 | −2.2143 | −1.7337 | −9.8613 | −18.6446 | −5.2516 | −6.7863 | −7.5504 |
| F12 | −0.3597 | −1.7677 | −4.6834 | −0.3603 | −5.6396 | −1.5826 | −4.4471 | −4.2187 |
| F13 | −2.7301 | −0.4901 | −0.0919 | −0.3719 | −6.9422 | −2.8672 | −4.9099 | −2.773 |
| F14 | 1.8927 | 2.3261 | 2.1197 | −0.2602 | 2.3072 | 0.9227 | 0.5609 | −0.0172 |
| F15 | −2.4831 | −1.7214 | −0.7624 | −1.2229 | −3.3176 | −0.8753 | −1.007 | −0.8751 |
| F16 | 2.2212 | 2.2212 | 2.2212 | 2.2208 | 2.2115 | 2.2212 | 2.2212 | 2.2212 |
| F17 | 1.5773 | 1.5859 | 1.5859 | 1.3679 | 1.5364 | 1.5394 | 1.5859 | 1.5859 |
| F18 | 1.8177 | 1.8177 | 1.8177 | −0.032 | 1.7296 | 1.8162 | 1.8177 | 1.8177 |
| F19 | 1.7638 | 1.8429 | 1.846 | 1.3821 | 1.7578 | 1.846 | 1.846 | 1.846 |
| F20 | 4.2008 | 6.558 | 6.773 | 5.1267 | 5.3109 | 6.7324 | 6.7188 | 6.6704 |
| F21 | 1.1336 | 5.7092 | 2.5958 | 3.1677 | 1.4626 | 1.4829 | 1.3288 | 1.2656 |
| F22 | 0.6817 | 8.8645 | 2.5775 | 2.4971 | 1.1771 | 1.9309 | 1.2734 | 1.7307 |
| F23 | 2.6481 | 8.174 | 2.7876 | 2.1375 | 2.7383 | 2.7022 | 2.5238 | 1.5677 |


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sengupta, S.; Basak, S.; Peters, R.A., II. Chaotic Quantum Double Delta Swarm Algorithm Using Chebyshev Maps: Theoretical Foundations, Performance Analyses and Convergence Issues. J. Sens. Actuator Netw. 2019, 8, 9. https://doi.org/10.3390/jsan8010009
Sengupta S, Basak S, Peters RA II. Chaotic Quantum Double Delta Swarm Algorithm Using Chebyshev Maps: Theoretical Foundations, Performance Analyses and Convergence Issues. Journal of Sensor and Actuator Networks. 2019; 8(1):9. https://doi.org/10.3390/jsan8010009
Chicago/Turabian StyleSengupta, Saptarshi, Sanchita Basak, and Richard Alan Peters, II. 2019. "Chaotic Quantum Double Delta Swarm Algorithm Using Chebyshev Maps: Theoretical Foundations, Performance Analyses and Convergence Issues" Journal of Sensor and Actuator Networks 8, no. 1: 9. https://doi.org/10.3390/jsan8010009
APA StyleSengupta, S., Basak, S., & Peters, R. A., II. (2019). Chaotic Quantum Double Delta Swarm Algorithm Using Chebyshev Maps: Theoretical Foundations, Performance Analyses and Convergence Issues. Journal of Sensor and Actuator Networks, 8(1), 9. https://doi.org/10.3390/jsan8010009