1. Introduction
Over the past few years, changing precipitation patterns have been linked to climate change and attracted worldwide attention [
1,
2,
3,
4]. Studies have shown that extreme precipitation events have increased over many regions around the world, altering the hydrological cycle, ecological environment, and different society activities, such as agriculture and hydropower generation [
5,
6,
7,
8,
9,
10,
11]. Even worse, according to numerical model simulations, these trends may continue into the next century [
12]. For example, an analysis based on global-scale observation datasets shows that extreme precipitation has expanded significantly over many mid-latitude regions of the Northern Hemisphere and that areas affected by drought or severe drought have increased since the 1970s [
13,
14,
15]. Therefore, it is important to analyze and predict changes in at different temporal and spatial scales around the world. Villarini et al. showed that increasing trends of heavy rainfall in the northern part of the central United States were related to expanded atmospheric moisture content due to rising temperatures [
16]. Related research found no significant trends in annual precipitation from 1956 to 2013 over mainland China, but regional differences were noted. For instance, reduced precipitation was observed mainly in central, southeastern, southwestern and northeastern China, whereas increased precipitation was detected mainly in the middle and lower reaches of the Yangtze River Basin (MLYRB), the southeast coastal region, the Qinghai-Tibet Plateau, and northwestern China; at the same time, frequencies of extreme precipitation events in these regions have also increased significantly [
17,
18,
19]. Studies have shown that the amount, intensity, and duration of extreme rainfall events in the MLYRB have all changed since the 1980s [
17].
To improve the quality of predicting regional extreme precipitation events, it is necessary to evaluate the mechanisms responsible for these precipitation changes. Among the different aspects of these mechanisms, the influences of large-scale circulation modes, which have strong impacts on extreme precipitation events, are particularly important [
20,
21]. Cayan et al. suggested that the frequency distribution of daily precipitation in winter over the western United States shows a strong and systematic response to the EI Niño-Southern Oscillation (ENSO) phases [
22]. Ning and Bradley also found that the ENSO phases have different influences on winter extreme precipitation events over the northeastern United States [
23]. In China, many studies have pointed out that abnormal changes in precipitation are often affected by sea surface temperature (SST) anomalies. For example, the influence of ENSO on autumn precipitation (AP) is more significant than that in summer; during an El Niño year, the AP usually appears reduced over North China and intensified in southern regions [
24]. In addition, during ENSO’s decaying years, its impacts on China’s climate have been promoted by the “capacitor effect” of the Indian Ocean SST [
25]. Related studies have shown that the Tropical Indian Ocean Dipole (TIOD) negative phase contributes to strengthening of the Indo-Burma trough in autumn, which further promotes the transport of water vapor to the Indian Ocean and South China Sea [
25,
26]. Complex sea–air interactions can also affect AP in the Yangtze River Basin during autumn [
27], for instance, the curvature of the summer Kuroshio Current axis, which is accompanied by large cold water masses in southern Japan. Correlation analysis has been extensively employed to assess the relationships between atmospheric circulation variability patterns and precipitation anomalies in China over the past 100 years [
28]. The Southern Oscillation (SO), North Pacific Oscillation (NPO), and 500 hPa atmospheric circulation W pattern (AECW) are some examples of atmospheric circulation variability affecting mid-latitude and tropical weather conditions, including China precipitation [
28]. Moreover, AP can be modulated by other low-frequency oscillations, such as the quasi-biennial oscillation (QBO) of the tropical stratosphere [
29].
Although relevant research has revealed important relationships between different modes of climate variability and AP variations in China [
25,
26,
27,
28,
29], the causal associations are still not fully understood. Furthermore, previous studies have focused on national or individual administrative divisions. In this study, we emphasize that there is more scientific and application value if assessing precipitation observations according to geographical characteristics. When examining the mechanisms modulating the large-scale circulation modes and related precipitation variability, physics-based regression modelling has been proposed to predict future precipitation events and effectively adopted to study summer precipitation forecasts in India, East Asia, and the MLYRB [
30,
31,
32,
33,
34]. However, few related studies have used such methods to explore spatiotemporal changes in AP over the MLYRB or employed related models for quantitative predictions [
34]. The MLYRB is not only a major agricultural base in China but also an area with strong societal and economic development [
34]. Autumn is the season in which the East Asian summer circulation transitions to the winter circulation [
35]. Many unstable factors may induce disasters, such as droughts, floods, and low temperatures [
36]. Therefore, it is not only important to analyze the major drivers affecting AP over the MLYRB, but equally relevant to investigate the feasibility of predicting precipitation with an appropriate regression model. In this study, we analyze the spatiotemporal variations of AP over the MLYRB from 1980 to 2015. The information flow detection method is employed to extract potential preceding predictors and compared to time-lagged correlation analysis to assess the usefulness of the information flow algorithm. Finally, the Bayesian linear regression (BLR) model is used to predict AP over the MLYRB.
5. Effectiveness of Predictors’ Detection Based on Regression Analysis
To further verify the usefulness of the NIF, this section evaluates the two most significant climate indices related to PC1 variability (EWI, TIOD) by computing the linear regression between these indices and different dynamic and thermodynamic variables affecting China AP [
57]. For comparison, similar regression analysis is also employed using the AECC index that showed weakest association with PC1. Regression coefficients are calculated using time-lagged anomalies with summer indices defined as predictors and AP as the predicted variable. In this article, we use the F test to test the significance of the regression coefficients. The F test is a test of the goodness of fit of the entire model, that is, the significance test of all variables to the explanatory variables [
25].
Figure 4,
Figure 5 and
Figure 6 show the variations in the regressed fields of the 700 hPa relative humidity, 850 hPa atmospheric circulation, and 500 hPa geopotential height with respect to the different climate indices. All of these regressed fields also support the conclusions provided by the NIF. As shown in
Figure 4, due to the anomalous east-west distribution of the tropical Pacific SST, a strong westward airflow was stimulated over the tropical Pacific, and an easterly airflow occurred in the Indian Ocean at 850 hPa. After the eastward airflow crossed the Indo-China Peninsula, the airflow turned into a southwestern airstream and entered southwestern China (the dashed squares in
Figure 4a and
Figure 5a). Furthermore, a large-scale anomalous southwesterly airflow over East China is observed. The 700 hPa relative humidity anomalies over the Indo-China Peninsula and Philippines (the dashed squares in
Figure 4c and
Figure 5c) are verified to be most likely related to the 850 hPa atmospheric circulation anomalies. These mechanisms are relevant to produce AP anomalies over the MLYRB, especially in the southern region, which is in good agreement with the spatial distribution of the first EOF mode. In
Figure 5, an easterly airflow was stimulated mainly over the tropical Indian Ocean owing to the TIOD. This easterly airflow was deflected to the north over the Indian Peninsula and then developed eastward, modulating a southwestern anomalous airflow over East China. Geopotential height anomalies were also enhanced in the India-Burma trough (the dashed squares in
Figure 4b and
Figure 5b), but it must be highlighted that this field passed only the 90% confidence interval test and not the 95% confidence interval test. In
Figure 6, the relative humidity and circulation fields showed weak regression coefficients, indicating that AECC has a negligible effect in modulating the first EOF mode. This finding is consistent with results presented in
Table 3. Therefore, the proposed NIF assessment can accurately reveal the most important climate drivers affecting the leading mode of AP variability over the MLYRB.
6. Prediction Experiment of AP over MLYRB
To achieve an acceptable prediction performance, we first obtain two ranked lists of climate indices ordered according to the values of the NIF and correlation coefficients based on
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11,
Table 12,
Table 13 and
Table 14. Then, as recommended by Song et al. [
60], we selected the top k factors from these two ranking lists, where
and
is the number of potentially selected indices. In this study, the number of climate indices is 13, and
k = 8. Thus, the top eight common indices in the two ranked lists are chosen as the final predictors. Following this procedure, KCS, TIOD, SIOD, EWI, WPSHA, and AO are the six most important predictors affecting PC1; NINO3.4, KCS, AECE, AECC, ECI, and QBO are the major predictors for PC2. Therefore, in this section, we analyze BLR prediction quality in coordination with these selected climatic factors and compare the BLR with the output of MLR, which is a common assessment in climate prediction. To reduce the impacts of the data from the current year on the forecasting results, when applying the MLR model, the regression forecast is performed with a cross-validation assessment excluding the target year. The BLR model can be simply expressed by Equation (4):
where g is a constant term and SX is a set of predictors with a, b, c, d, e, and f being their corresponding parameters. The histograms of the regression parameters
are shown in
Figure 7 and
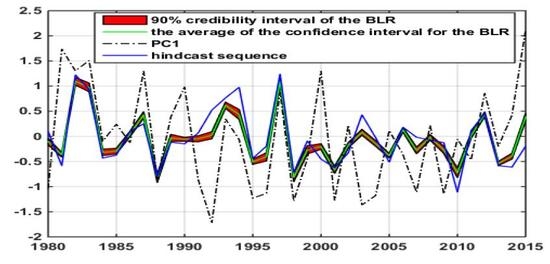
Figure 8. The final regression results are shown in
Figure 9 and
Figure 10, where the red area represents the 90% confidence interval predicted by BLR and the green solid line represents the interval average predicted by BLR. The multiple correlation coefficient (MCC) and root mean square error (RMSE) are introduced to measure the specific performance of the forecast results [
46]. Regression assessment is calculated using time-lagged anomalies, which considers using summer indices to predict AP anomalies.
According to the regression results for the time series of PC1 (
Figure 9), the BLR model captured the decreasing trend in 2006–2007, the increasing pattern in 2007–2008 and 2011-2012, the decreasing trend in 2012, and the increasing pattern in 2013. From the comparison results in
Table 15, the prediction results for the first mode of the BLR model are more satisfactory than those of the MLR model; the MCC of the BLR model is 0.5299, and the RMSE is 0.8508, which are significantly better than those of the MLR model. The BLR model forecast quality, when evaluated by the MCC and RMSE scores, showed an improvement of around 40% compared to the MLR model. The related forecasting results also reflect how useful the NIF assessment is for extracting potential forecasting factors from the margins of the studied domain. Compared to the traditional scheme (MLR) [
33,
34], the BLR scheme better predicts the trend of interannual changes in AP over the MLYRB.
The prediction results for the PC2 time series (
Figure 10) reveal that the BLR captured the upward trend in 1989–1991, the downward pattern in 1991–1992 and 2002–2003, the decreasing trend in 2013, and the increasing pattern in 2015. As seen from
Table 16, the performance of the BLR is also satisfactory, with an MCC of 0.6727 and an RMSE of 0.7358. A comparison between BLR and MLR models shows that the former forecast quality, when evaluated by the MCC and RMSE scores, showed an improvement around 35% and 26% compared to the latter, respectively.
7. Discussion
Although the prediction skills of AP over the MLYRB using the NIF-BLR model are superior, there are still some limitations. First, most of the climate indices proposed in this study were selected from previous research, which led to certain subjectivity in the evaluation process. As a future step, we will further develop research combining numerical forecasting model products to improve the quality of forecasts. Second, if the cycle of the regression model changes, this may lead to a decrease in the prediction skill. Thus, the prediction model established in this study may not be fully applicable to other periods. Therefore, in the later period, we will carry out further research in combination with numerical forecasting models to improve the quality of forecasts. One way to undertake this evaluation is using the projection of the model’s hindcast anomalies (we will select an appropriated climate model for providing hindcast data) onto the two observed leading eigenvectors (we already have this) to obtain the corresponding forecasted PC time series. Despite these potential limitations, the prediction factors and precipitation prediction results identified in this study will help us to better understand the variability in autumn precipitation over the MLYRB and improve the regional prediction of autumn precipitation elsewhere. These findings may also help policymakers and decision makers to prepare appropriate adaptation and mitigation measurements for future climate change.
8. Summary
This study investigated the characteristics of AP anomalies over the MLYRB by exploring the leading spatial-temporal modes and potential predictors driving the precipitation variability. The main conclusions are as follows:
(1) Regarding EOF analysis, the MLYRB is a region with significantly varying AP. The contribution of the variance in the first leading mode is 30.83% and shows a monopole with different precipitation amounts over the whole region. The second mode explains 16.13% of the total variance, and its spatial distribution function is characterized by a meridional dipole. The time series of the first two PCs shows marked interannual variations, but weak interdecadal signals.
(2) To achieve an acceptable prediction performance, we firstly obtained two ranked lists of climate indices ordered according to the values of the NIF and correlation coefficients. Then, as recommended by Song et al. [
60], we selected the top eight factors from the two ranked lists. Thus, the top eight common indices in the two ranked lists were chosen as the final predictors. Following this procedure, KCS, TIOD, SIOD, EWI, WPSHA, and AO are the six most important predictors affecting the first EOF mode of AP over the MLYRB, whereas NINO3.4, KCS, AECE, AECC, ECI, and QBO are the major predictors for the second mode.
(3) We considered the time series prediction of the first two PCs as a small-sample problem; therefore, the BLR model could be adopted. From the experimental results, BLR captured the PC1 and PC2 trends, and the overall performance was relatively satisfactory. Finally, the BLR demonstrates the ability to improve upon the MLR model.