Concepts for Increased Energy Dissipation in CFRP Composites Subjected to Impact Loading Conditions by Optimising Interlaminar Properties

Abstract

Carbon fibre-reinforced plastics (CFRP) are predestined for use in high-performance components due to their superior specific mechanical properties. In addition, these materials have the advantage that the material properties and in particular, the failure behaviour can be adjusted. Fibre-dominated failure modes are usually brittle and catastrophic. In contrast, delaminations successively absorb energy and retain in-plane structural integrity. Previous investigations have shown that interface modifications can be used to selectively adjust the interlaminar properties, which decisively influence the delamination behaviour and the associated failure behaviour of structures. However, a systematic analysis of the influences of the positioning and characteristics of the interface modifications on the structural failure behaviour is still missing. Based on existing experimental investigations on the energy dissipation of CFRP impact-loaded beams, the failure behaviour is described here with the help of numerical simulations. The structural failure behaviour and the energy dissipation are represented in a three-dimensional, parameterised finite element analysis (FEA) model. Furthermore, the parameterised models are used to maximise the energy absorption of the three-point bending test through three concepts of interface modification. The large number of model input parameters requires a metamodel-based description of the correlation between the positioning and characteristics of the interface modification and the energy dissipation. Within the scope of the present work, a procedure is therefore developed which enables an efficient design of interface-modified CFRP under impact loads.

1. Introduction

With their highly specific mechanical properties, carbon fibre-reinforced plastics (CFRP) are suitable for use in high-performance components such as crash- and impact-loaded structures such as composite fan blades [1,2]. In addition, these materials have the advantage that the material properties and especially the failure behaviour can be adjusted. The focus is mostly on the adaption of the fibre orientation to the dominant stress in order to increase the stiffness and strength of the materials [3]. This approach often leads to a brittle failure behaviour of the corresponding structures so that on the one hand, the structural integrity is compromised, and on the other hand, the energy absorption capacity is not optimally utilised [4].

Besides the choice of fibre and matrix material as well as the textile architecture, there are essentially two approaches for increasing the energy absorption of fibre-reinforced plastics. Firstly, the fibre–matrix adhesion is specifically adjusted by influencing the boundary layer during manufacturing. Initial work on this goes back to [5], where the influence of the adhesion properties of an epoxy matrix to boron filaments and their influence on the fracture toughness of such composites is described. The work in [6] follows this approach and shows that the fracture toughness is further increased by alternating high and low fibre–matrix bonds along the fibres. Secondly, especially in multi-layered composites, suitable interlayers are inserted through the concept of controlled interlaminar bonding. In this methodology, primarily thermoplastic interlayers are inserted into layer-based thermoset composites. A good overview of methods that lead to an improvement of the interlaminar properties by interleaved layers on a thermoplastic basis, but also to a more brittle failure behaviour with lower energy absorption, is given in [7]. In contrast, methods with lower interlaminar properties generally result in significantly higher energy absorption with improved structural integrity and a moderate decrease in structural strength [8,9,10].

The mentioned studies are exclusively experimental, and their conclusions are based on purely empirical statements. The study presented here, however, introduces a simulation approach that can be used to identify, analyse, and target the phenomenology of the energy absorption mechanisms of impact-loaded composite structures. A methodology is presented that describes the interface modification of CFRP in the framework of finite element analysis (FEA) up to the structural scale. Thus, this approach can be used to extend the experimental database with virtual tests. Finally, it is shown how the interface modification approach can be adapted to an optimisation process [11,12]. Thus, it is possible to derive concepts with which the energy absorption behaviour of impact-loaded CFRP structures can be significantly increased.

2. Materials and Methods

Deformation, damage, and failure behaviour of interface-modified CFRP beams is investigated numerically based on the experimental data of [10]. An interfacial modification by means of perforated polytetrafluoroethylene (PTFE) foil is used (Figure 1a). Figure 1b shows the geometric dimensions of the perforated PTFE foil.

As PTFE does not adhere to the composite material, the interface properties are influenced exclusively by the geometric (mesostructural) dimensions and can be adjusted by the so-called interlaminar contact area $\kappa$:

$$\kappa =\frac{2 a^2}{d^2}.$$

(1)

In the experimental study, a constant value of 4 mm was chosen for the edge length of the perforation a [13]. Based of targeted interlaminar contact area $\kappa$, the distances between two perforations b and the length of the unit cell d are derived. The investigations are carried out using the example of a plain weave fabric composite based on a HexPly M49 200P prepreg semi-finished product from Hexcel. Consolidation is carried out in an autoclave process according to the manufacturer’s specifications, resulting in an average fibre volume content of 55% [14]. Further details about the physical and mechanical properties are shown in

Table A1. HexPly M49 200P data sheet from supplier.

Prepreg Property		Quantity	Unit
Fibre		HS Carbon
Tow		3K
Weave		Plain
Nominal cured ply thickness		0.234	mm
M49 resin content by weight		42	%
Mechanical property for 55% fibre volume content	Test method
Tensile modulus in fibre direction	EN 2561	64,000	MPa
Tensile strength in fibre direction	EN 2561	900	MPa
Compressive strength in fibre direction	EN 2850B	725	MPa
Bending modulus in fibre direction	EN 2562	52,000	MPa
Bending strength in fibre direction	EN 2562	850	MPa
Interlaminar shear strength	EN 2563	63	MPa

in Appendix A.

2.1. Influence of Interface Modification on In-Plane Properties

To determine the influence of the interlaminar interface modification on the in-plane properties of the composite, tensile tests according to DIN EN ISO 527-4 are performed. The rectangular specimens were 200 mm long, 25 mm wide, and 2 mm thick and were tested with a loading velocity of 0.5 mm/s. Figure 2a shows the fracture patterns of exemplary tensile specimens with the respective contact surface proportions κ. The fracture surfaces of specimens with high contact area fractions show smooth fracture surfaces, while specimens with low contact area fractions show more jagged fracture patterns. This behaviour is a consequence of different load redistribution processes during damage propagation. When a single layer of a specimen with high interlaminar properties fails, the load is redistributed to the other layers. These are subsequently overloaded in the immediate vicinity of the first point of damage and subsequently fail there. In contrast to test specimens with a high contact area, test specimens with a smaller contact area show a different failure mechanism. If a single layer in the laminate with low interlaminar properties fails, the crack does not run into the adjacent layers, but separates and decouples the individual layers from each other. This causes the adjacent individual layers to fail at their respective weak points, which do not necessarily have to be close to the position of the original initial failure.

The Young’s modulus remains almost constant with the increasing contact area κ. The strength, however, increases with increasing contact area κ, which is due to an influence on the local stress state as a result of the perforation as an interference point. Additionally, the load transfer between the individual layers is limited by the low interlaminar property. The investigations carried out here prove that the in-plane properties under tensile load are not significantly influenced by the selected type of interface modification.

The in-plane failure behaviour is described by an adaptation of Hashin’s failure theory [15]. Here, no interaction between tensile ${\sigma }_{11}$ and shear stresses ${\sigma }_{12}$ and ${\sigma }_{13}$ in tensile fibre mode is assumed:

$$\frac{{\sigma }_{11}}{xt}=1, \mathrm{for} {\sigma }_{11}>0.$$

(2)

The fibre compressive mode is modelled analogously:

$$\frac{\left|{\sigma }_{11}\right|}{xc}=1, \mathrm{for} {\sigma }_{11}<0,$$

(3)

where xt and xc are the tensile and compressive strengths in the fibre direction. Failure in the 2-direction is also modelled as fibre failure for woven fabrics due to symmetry. Since out-of-plane failure is modelled with the cohesive element approach, the out-of-plane failure mode is supressed by setting strengths to very high values for the single-ply material model. The LS-DYNA material model 58 (*MAT_058) [16] is used for modelling. MAT_058 also enables the modelling of damage evolution using the Matzenmiller model [17]. The material’s stiffness is gradually degraded until a residual level of stress (slimt1, slimc1) is reached. This is kept constant until the final failure strain (fail1, fail2) is reached. Since the material can still transfer loads in compression failure, higher values are assumed for slimc1 and fail2 than for the corresponding values for tensile failure slimt1 and fail1. Figure 3 shows the modelled stress–strain curve in the fibre direction.

Table 1. Material properties used for three-point bending model.

Property	Symbol	Quantity	Unit
Elastic
Young’s modulus in fibre direction	ea, eb	53,300	MPa
Young’s modulus in through-thickness direction	ec	10,000	MPa
Poisson ratio in-plane	prba	0.085	-
Poisson ratio out-of-plane	prca, prcb	0.0185	-
Shear modulus in-plane	gab	4099	MPa
Shear modulus out-of-plane	gbc, gca	1775	MPa
Strength
Tensile strength in-plane	xt, yt	994	MPa
Compressive strength in-plane	xc, yc	1081	MPa
Shear strength in-plane	sc	100	MPa
Post failure
Factor of minimum stress for fibre tension	slimt1, slimt2	0.03	-
Factor of minimum stress for fibre compression	slimc1, slimc2	0.581	-
Factor of minimum stress for in-plane shear	slims	0.950	-
Failure strains (element deletion)
Tensile failure strain in fibre direction	fail1, fail3	0.030	-
Compressive failure strain in fibre direction	fail2, fail4	0.115	-
Shear failure strain in-plane	fail5	0.400	-

shows the key material parameters. The full LS-DYNA material cards are shown in

Table A2. Used LS-DYNA material card *MAT_058 in unit system t-mm-s-N.

*MAT_LAMINATED_COMPOSITE_FABRIC_SOLID
$	mid1	ro	ea	eb	(ec)	prba	tau1	gamma1
	58	1.47e-09	53300	53300	10000	0.085	42.4	0.007
$	gab	gbc	gca	slimt1	slimc1	slimt2	slimc2	slims
	4099	1175	1175	0.03	0.581	0.03	0.581	0.95
$	aopt	tsize	erods	soft	fs	epsf	epsr	tsmd
	0.0	0.0	0.0	0.0	−1.0	0.0	0.0	0.9
$	xp	yp	zp	a1	a2	a3	prca	prcb
	0.0	0.0	0.0	0.0	0.0	0.0	0.0185	0.0185
$	v1	v2	v3	d1	d2	d3	beta	lcdfail
	0.0	0.0	0.0	0.0	0.0	0.0	0.0	11
$	e11c	e11t	e22c	e22t	gms
	0.0	0.0	0.0	0.0	0.345
$	xc	xt	yc	yt	sc
	1081	994	1081	994	100
$	e33c	e33t	gm23	gm31
	0.0	0.0	0.0	0.0
$	zc	zt	sc23	sc31
	10000	10000	10000	10000
$	slimt3	slimc3	slims23	lsims31	tau2	gamma2	tau3	gamma3
	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
$	lcxc	lcxt	lcyc	lcyt	lcsc	lctau	lcgam	dt
	0	0	0	0	0	0	0	0.0
$	lce11c	lce11t	lce22c	lce22t	lcgms	lcefs
	0	0	0	0	0
$	lczc	lczt	lcsc23	lcsc31	lctau2	lcgam2	lctau3	lcgam3
	0	0	0	0	0	0	0	0
$	lce33c	lce33t	lcgms23	lcgms31
	0	0	0	0
$: comment lines.

and

Table A3. Used failure strains.

*DEFINE_CURVE
$	lcid	sidr	sfa	sfo	offa	offo	dattyp	lcint
	11	0	1	1	0	0	0	0
$		a1		o1
		1		0.030
		2		0.115
		3		0.030
		4		0.115
		5		0.400
		6		1.0
		7		1.0
		8		1.0
$: comment lines.

in Appendix A.

2.2. Influence of Interface Modification on Out-of-Plane Properties

The influence of the interlaminar contact area proportion on the delamination behaviour is investigated using five pre-cracked double cantilever beam (DCB) test specimens. The specimens have an interlaminar contact area $\kappa$ of approx. 0.15, 0.30, 0.45, and 1.0, respectively, and are tested according to ISO15024. The results are presented in Figure 4. The relationship between through-thickness strength, the strain energy release rate, and $\kappa$ is reasonably well-represented by a linear fit.

Cohesive zone approaches are used for modelling delamination between adjacent single plies. They allow an evaluation of the delamination initiation and a description of the delamination growth. LS-DYNA offers cohesive zone models as part of contact formulations or through special cohesive elements.

The accuracy of cohesive elements is higher in comparison to contact formulations [18]. Therefore, cohesive elements with a bilinear material model are used here for modelling the delamination behaviour of interface-modified multilayer composites.

Table 2. Cohesive properties.

Property	Symbol	Quantity	Unit
Elastic
Normal stiffness	en	5 $\times$ 106	N/mm3
Shear stiffness out-of-plane	et	1 $\times$ 106	N/mm3
Strength
Normal tensile strength	t	32	MPa
Shear strength out-of-plane	s	50	MPa
Post failure
Normal strain energy release rate	gic	0.96	kJ/m2
Shear strain energy release rate	giic	2.50	kJ/m2

shows the key parameters for the cohesive model without interface modification ($\kappa$= 1.0). The full LS-DYNA material card is shown in

Table A4. Used LS-DYNA material card *MAT_138 for cohesive elements without interface modification ($\kappa$ = 1.0) in unit system t-mm-s-N.

*MAT_COHESIVE_MIXED_MODE
$	mid	ro	roflg	intfail	en	et	gic	giic
	138	1.56e-09	53300	1.0	5.0e+06	1.0e+06	0.96	2.50
$	xmu	t	s	und	utd	gamma
	2.0	32.0	50.0	0.0	0.0	1.0
$: comment lines.

in Appendix A. The parameters of the strengths (t and s) and the critical energy release rates (gic and giic) are adjusted to account for the interface modification in the material model. Since PTFE does not adhere to the composite material, the interlaminar properties of the strengths and strain energy release rates are also zero at $\kappa =0$ (no perforation, intact release foil). A linear relationship between the interlaminar contact area and strain energy release rate in Mode I applies to both the strengths and the characteristic values in the Mode II load case (Figure 4).

2.3. Three-Point Bending Test Simulation

The influence of the interface modification on the structural deformation and failure behaviour is investigated by modelling an impact-loaded three-point bending beam setup (Figure 5a). The supports and the load introduction are modelled with rigid shell elements. The indenter moves downwards at a constant velocity of 2 m/s for a total displacement of 20 mm. Each prepreg layer is modelled by two elements in the thickness direction using reduced integrated hexahedral elements (ELFORM 1). The element size is 1 mm in the longitudinal axis and 3.33 mm in the width direction, resulting in 5964 solid elements. In addition, potential delamination layers are distributed symmetrically to the centre plane corresponding to the experimental setup [10] with 1 µm thick cohesive elements (ELFOR 19), resulting in 1065 cohesive elements. A segment-based automatic surface-to-surface contact with a friction coefficient of 0.3 [19] is used to enable contact between the composite plies after the cohesive elements have failed.

The test is evaluated using the force–displacement curve (Figure 5b). The curve’s integral equals the total absorbed energy E_T. The integral up to the force maximum is referred to as initiation energy E_I and corresponds largely to the elastic energy stored in the test specimen. The remaining energy is referred to as propagation energy E_P and is largely related to damage and failure processes in the test specimen.

To improve the energy absorption capacity of impact-loaded CFRP structures, the total energy absorbed E_T should be maximised. In the case presented here, this can be achieved by maximising the propagation energy without significantly reducing the initiation energy. Furthermore, the structural integrity of such CFRP composites can be improved by the initiation and propagation of delaminations.

2.4. Optimisation Strategies

The desired increase of energy absorption and structural integrity of the impact-loaded CFRP beam is approached using three different interface designs (Figure 6). The interlaminar properties of all five interfaces are uniformly weakened by varying the interlaminar contact area in design A (Figure 6a). Design B establishes whether a layer-by-layer weakening of the interface leads to a further increase in energy absorption (Figure 6b). Finally, sectional interface modifications are used in the third concept to determine which positions are particularly suitable for weakening in design C (Figure 6c).

The software LS-Opt is used to carry out the optimisation [20]. A metamodel-based optimisation of the resulting 15 model input parameters is performed using a sequential approach, which reduces the parameter space in each iteration (see Figure 7).

A design of experiment (DoE) is created using Latin hypercube sampling. FE simulations are then generated for each parameter set. Based on these results, a feedforwarded neural network (FFN) metamodel is trained using standard LS-Opt settings. The FFN approximates the relationship between the interface parameters ${\kappa }_i$ and the total energy absorption E_T. The input parameters are then optimised based on the predictions of the metamodel. The ASA (adaptive simulated annealing) algorithm is used for optimisation. The sequential optimisation is terminated when the parameter sets or the objective function differ less than 1% from the previous iteration. If this is not the case, new parameter sets are generated, whereby the parameter set domain is reduced by 20%.

3. Results

First, the FEA model is evaluated regarding its predictive quality for representing the complex deformation and failure behaviour. Then, the results of the optimisation for the three interface designs are presented.

3.1. Model Validation of the Reference Model

Figure 8 shows a comparison of the deformation and failure behaviour of impact-loaded CFRP beams with different interface modifications (design A) based on both experimental and numerical analyses. In the case of no interface modification ${\kappa }_i=1$, the specimen fails brittle and central. This is well-predicted by the simulation. When the interfacial property is weakened (${\kappa }_i=0.3)$, a delamination failure occurs as initial failure mode on only one side of the specimen with a subsequent fibre failure. This sequence is not predicted accurately by the simulation. The model predicts a symmetrical delamination failure on both sides of the specimen, which is due to the assumed perfect symmetry. Nevertheless, this FEA model can be used to investigate the influence of the interface design on the structural behaviour since the key failure modes are captured by the model.

3.2. Energy Absorption Capacity of Optimised Interface Modification Designs

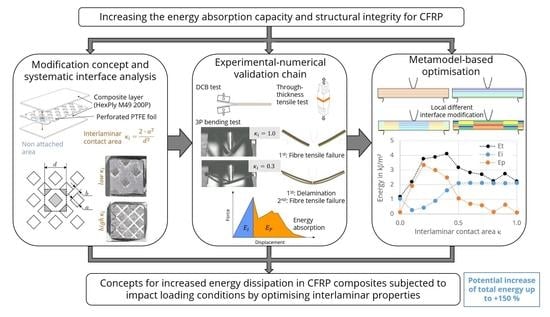
The following section presents the results of optimising the interface designs for improved energy absorption and structural integrity.

3.2.1. Design A (Same Layer-by-layer Interface Modification Concept—Figure 6a)

Figure 9 shows the energy absorption of the impact-loaded CFRP beam with different interlaminar contact areas $\kappa$. Figure 5b displays the various energies as functions of contact area. The total energy E_T is the sum of the initiation E_I and propagation energy E_P.

The simulation with a contact area ($\kappa =0.0)$ shows a very compliant structural response, as the whole specimen is already delaminated in the simulation. It also shows no in-plane failure until the specimen slips through the support, and the force signal increases continuously from this point on. After the slippage, there is still some force transfer due to inertia and friction from the contact of the indenter with the specimen. However, these effects are neglectable; therefore, the energy absorption capacity of this interface modification is largely determined by the initiation energy.

From a κ of 0.1, E_I increases as the force rises more steeply due to a higher initial stiffness. Compared to the case κ = 0.0, E_I is lower for κ = 0.1. Although the maximum force is much higher, the displacement at maximum force is lower due to the much higher stiffness, resulting in lower E_I. Since the interlaminar properties of strengths (t and s) and critical energy release rates (gic and giic) are very low, extensive delamination occurs in all five interfaces from the time the maximum force is reached. As a result, E_P is significantly higher than E_I. In general, this indicates that an increasing contact area leads to an increased E_I due to the higher force maxima caused by increasing interlaminar strengths. However, at contact areas of 0.5 and above, the initial failure is no longer dominated by delamination failure, but by fibre failure. This is why the initiation energy remains almost constant from this interface modification onwards.

E_P decreases starting from $\kappa$ = 0.2. Due to increasing interface strengths, not all five modified interfaces delaminate and dissipate energy accordingly. Reduced delamination occurs since the initial failure is determined by the in-plane failure. This trend intensifies above a $\kappa$ of 0.5. E_P decreases with increasing interlaminar contact area and approaches zero. The small increase in the propagation energy at $\kappa$= 0.9 results from a subsequent force effect on the indenter due to a collision with the refracted beam arms and thus represents a numerical artefact.

In reference [10], the amounts for the interlaminar contact area are given as nominal values. For comparison with the simulations presented here, it is necessary to use the precise values for the specimens resulting from the manufacturing process.

Table 3. Nominal values [10] and values resulting from the manufacturing process for interlaminar contact area.

Interlaminar Contact Area $\mathit{\kappa }$
Nominal [10]	0.20	0.40	0.60	1.00
Real	0.15	0.31	0.46	1.00

contains these values, and Figure 10 compares the results from [10] with the simulation results based on the methods used here.

Generally, the numerical model is capable of reproducing the complex deformation and failure behaviour of the impact-loaded CFRP beams. The simulations significantly underestimate the initial energy for a small contact area $\kappa$. The experimentally determined force–displacement curve is clearly nonlinear until the maximum force is reached. This rather gradual failure is explained by smaller delamination processes [10]. In contrast, the simulations predict a strongly linear force–displacement curve until a sudden large-scale delamination failure, which leads to an abrupt drop in force and the corresponding lower E_I. For the case of $\kappa =0.46$, E_I is overestimated by the simulation as delamination failure is predicted at a higher force. The model of a fully interlaminar contact area predicts E_I with very good agreement with the experimental values.

All simulations overestimate E_P with the exception of the models with a $\kappa$ of 1.0. This is caused by the symmetrical formation of delaminations. Nevertheless, E_T as the sum of E_i and E_P is predicted sufficiently well by the simulation models within the standard deviation of the experimental results, except for the results of $\kappa =0.46$. Due to the moderate interface properties, the energy absorption in this case is higher due to overestimated delaminations than in the simulation with smaller $\kappa$.

The inserted foil increases the mass of the tested samples by 6–8% according to the chosen interlaminar contact area. This is negligible compared to the scattering of the energies. The mass is not varied in the simulation because the thickness and density of the cohesive elements are not varied with $\kappa$.

The numerically derived data are used to calibrate the FNN metamodel. The accuracy of the metamodel for Design A’s concept is determined by the coefficient of determination $R_A^2$:

$$R_A^2=\frac{{{\displaystyle \sum }}_{n=1}^p{\left({\widehat{E}}_n\left(\kappa \right)-\overline{E}\left(\kappa \right)\right)}^2}{{{\displaystyle \sum }}_{n=1}^p{\left(E_n\left(\kappa \right)-\overline{E}\left(\kappa \right)\right)}^2}=0.919$$

(4)

where p is the number of data sets, ${\widehat{E}}_n$ is the predicted total energy,$\overline{E}$ is the mean of the analysed total energy, and $E_n$ is analysed total energy with respect to the parameter set $\kappa$. The metamodel is then used to determine a parameter set $\kappa$ in which $E_T$ is maximised. Mathematically, the task can be formulated as follows:

$$\left\{\begin{array}{c}\underset{\kappa }{\max }{\widehat{E}}_n\\ 0\le \kappa \le 1\end{array}\right.,$$

(5)

where no further constraints for $\kappa$ have to be fulfilled. An interlaminar contact area of 0.45 would result in the largest energy absorption of 4.9 J according to the metamodel predictions. This is an increase of about 120% compared to the reference model. Even if this value appears somewhat too optimistic due to the overestimated delamination energy, the simulation models and the applied metamodel-based optimisation confirm the results of the experimental investigations. The energy absorption can be significantly increased by the specific adjustment of the interlaminar properties and the resulting delamination behaviour.

3.2.2. Design B (Layer-Wise Interface Modification Concept—Figure 6b)

In the layer-wise modification concept, the interlaminar properties of all five interfaces are varied independently. This extends the parameter space to be investigated from one to five interlaminar contact areas ${\kappa }_i$ with $i=1,2,\dots ,5$. A total of 150 parameter sets p are simulated. For the investigated metamodel,

$$R_B^2=\frac{{{\displaystyle \sum }}_{n=1}^p{\left({\widehat{E}}_n\left({\kappa }_i\right)-\overline{E}\left({\kappa }_i\right)\right)}^2}{{{\displaystyle \sum }}_{n=1}^p{\left(E_n\left({\kappa }_i\right)-\overline{E}\left({\kappa }_i\right)\right)}^2}=0.862$$

(6)

Again, the metamodel is then used to determine a parameter set ${\kappa }_i$ in which $E_T$ is the maximum:

$$\left\{\begin{array}{c}\underset{{\kappa }_i}{\max }{\widehat{E}}_n\\ 0\le {\kappa }_i\le 1\end{array}\right..$$

(7)

where no further constraints for ${\kappa }_i$ have to be fulfilled.

Table 4. Optimal interlaminar contact areas ${\kappa }_i$ for the layer-wise interface design.

Layer-Wise Interlaminar Contact Areas ${\mathit{\kappa }}_{\mathit{i}}$
${\kappa }_1$	${\kappa }_2$	${\kappa }_3$	${\kappa }_4$	${\kappa }_5$	$E_T$
0.32	0.51	0.44	0.44	0.30	5.18 J

shows the optimal contact areas ${\kappa }_i$ for the five layer-wise interface modifications. Overall, the values deviate slightly from the optimal value of $\kappa$ for design A. Smaller values are obtained for the outer interfaces due to the low shear stress. The value of the energy absorption is only slightly higher than for the same interface modification, which is also due to the fact that the contact area does not change significantly.

3.2.3. Design C (Sectional Interface Modification—Figure 6c)

In the sectional interface modification, the five interfaces of the layer-wise concept are each divided into three sections, taking symmetry into account. For the creation of the metamodel, 205 parameter sets (p) for the 15 interlaminar contact areas ${\kappa }_i$ with $i=1,2,\dots ,15$ are analysed. The developed metamodel has an accuracy $R_C^2$ of 0.689. The driving assumption of design C is the identification of the influence of specific locations for interface modifications on the global energy dissipation. Therefore, the influence of ${\kappa }_i$ on the structural response of the three-point bending test is determined using a variance-based sensitivity analysis [21]. A global sensitivity analysis (GSA) index is determined for each ${\kappa }_i$, which describes the influence of the parameter on $E_T$. The sum of the indexes is normalised to 1.

Figure 11 shows the GSA index of the 15 interfaces. This shows that interface 3 has the greatest influence on energy absorption. Interfaces 2 and 4 are of secondary importance, and interfaces 1 and 5 are almost negligible. The inner interfaces seem to have a slightly greater influence on the structural behaviour than the middle interfaces, with the exception of interface 3. The inner interfaces in interface 1 are important because of the bulging effect, which describes delamination initiation due to local buckling of the upper plies under the compressive load. The outer interfaces have no significant influence on the structural behaviour.

It can therefore be assumed that the out-of-plane regions subjected to shear stress are especially responsible for the delamination initiation and propagation because the three-point bending induces shear stress and it is not an edge effect. Otherwise, the outer interface design would have a greater GSA index.

4. Discussion and Conclusions

The delamination behaviour is promoted by selectively weakening the interlaminar properties of the impact-loaded CFRP beams via modified interfaces. This leads to an improved post-failure behaviour in terms of an increased energy absorption and thus improved structural integrity (Figure 10).

The used FEA modelling approach replicates the complex deformation and failure behaviour accurately and can model the trends of initiation and propagation energies for varying interlaminar contact areas $\kappa$. Future investigations should use improved discretisation in the delamination direction so that more cohesive elements are included in the delamination zone.

The sensitivity of delamination behaviour with respect to a deviation of the impact position should be investigated. It is possible that slightly offset impact positions in the experiments are responsible for the one-sided delamination formation. Additionally, stochastically distributed properties in the interfaces could be used to avoid the strict symmetry of failure observed in the simulations and thus improve the agreement between the simulation and experiments.

The failure behaviour of the single plies and delaminations can be described separately due to the negligible influence of the interface modification on the in-plane properties. The material model and the bilinear cohesive approaches describe the failure behaviour sufficiently accurately. The parameterisation of the cohesive properties based on the interlaminar contact area $\kappa$ enables the adjustment of the interlaminar properties and thus the use within a DoE study. The optimisation framework employed here resulted in reasonable predictions for optimised interlaminar contact areas and is suitable for the three-point bending test investigated as part of this study.

Three distributions of the adapted interface modifications are investigated: design A—same layer-by-layer, design B—layer-wise, and design C—sectional interface modifications.

With the same layer-by-layer optimisation, a maximum possible energy absorption was determined at $\kappa$ = 0.45. There, E_T is about 120% higher in comparison to the reference specimens without modification. The results for $\kappa$ after the optimisation for the layer-wise interface modification are between 0.30 and 0.51 and thus deviate only slightly from the result of the layer-by-layer interface modification. The reason for this is that the energy absorption is particularly high when a maximum of delamination processes are initiated. The fact that the delaminations occur as a result of shear stress rather than as the consequence of an edge effect is revealed by the results of the sectional interface modification.

In summary, the results of the experimental work [10] are confirmed by the presented investigations. The observed effect of built-in interface defects was numerically confirmed. The adjusted interface modification significantly influences the energy absorption capacity of CFRP beams subjected to bending loads. Optimisation was successfully employed to maximise the total energy absorption.