Robust Design Optimization of Supersonic Biplane Airfoil Using Efficient Uncertainty Analysis Method for Discontinuous Problem
Abstract
:1. Introduction
2. Uncertainty Analysis Methods
2.1. MCS (Monte Carlo Simulation)
2.2. DDF (Divided Difference Filter)
2.3. IMCS (Inexpensive Monte Carlo Simulation)
2.4. Divided IMCS
3. Numerical Schemes
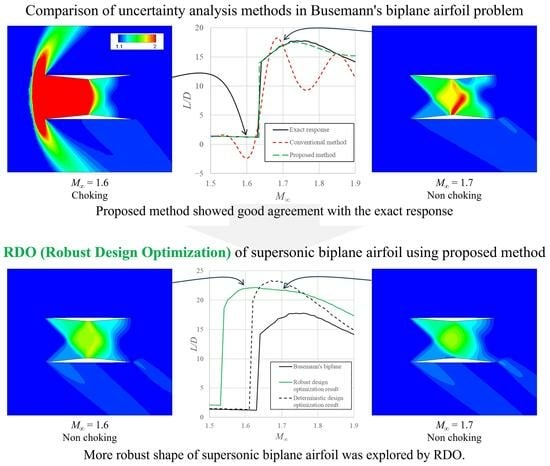
4. Comparison of Uncertainty Analysis Methods
5. Robust Design Optimization (RDO) Problem
5.1. Definition of the Optimization Problem
5.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A


| Method | Cd | L/D | Computational Cost 2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | ||||||
| MCS | 1.43 × 10−2 | 0% | 2.38 × 10−2 | 0% | 15.2 | 0% | 4.38 | 0% | 1000 |
| DDF | 2.11 × 10−2 | 48% | 3.22 × 10−2 | 35% | 14.2 | −7% | 5.92 | 35% | 5 |
| IMCS | 1.08 × 10−2 | −24% | 2.53 × 10−2 | 6% | 11.6 | −24% | 3.43 | −22% | 18 |
| divided IMCS (α = 0.5) | 1.48 × 10−2 | 3% | 2.40 × 10−2 | 1% | 15.1 | −1% | 4.40 | 0% | 18 |
References
- Kusunose, K. Aerodynamic Design of Supersonic Biplane: Cutting Edge and Related Topic; Tohoku University Press: Sendai, Japan, 2007. [Google Scholar]
- Kusunose, K.; Matsushima, K.; Maruyama, D. Supersonic biplane—A review. Prog. Aerosp. Sci. 2011, 47, 53–87. [Google Scholar] [CrossRef]
- Yamazaki, W.; Kusunose, K. Biplane-Wing/Twin-Body-Fuselage Configuration for Innovative Supersonic Transport. J. Aircr. 2014, 51, 1942–1952. [Google Scholar] [CrossRef]
- Suga, Y.; Yamazaki, W. Aerodynamic Uncertainty Quantification of Supersonic Biplane Airfoil via Polynomial Chaos Approach. In Proceedings of the 17th AIAA Non-Deterministic Approaches Conference 2015, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Yamazaki, W.; Suga, Y. Comparison of Uncertainty Quantification Approaches in a Supersonic Biplane Airfoil Problem. Trans. Jpn. Soc. Aero. Space Sci. 2017, 60, 10–17. [Google Scholar] [CrossRef]
- Ban, N. Efficient Aerodynamic Topology Optimization on Supersonic Flow Field via Machine Learning Technologies. Ph.D. Thesis, Nagaoka University of Technology, Niigata, Japan, 2019. [Google Scholar]
- Tabata, S.; Hanazaki, K.; Yamazaki, W. Uncertainty Quantification and Robust Design Optimization of Supersonic Biplane Airfoils. Trans. Jpn. Soc. Aero. Space Sci. 2020, 63, 233–242. [Google Scholar] [CrossRef]
- Kawai, S.; Yamazaki, W.; Oyama, A. Uncertainty Quantification of Supersonic Biplane Airfoil by Multi-Element Polynomial Chaos Based on Edge Detection. In Proceedings of the AIAA Science and Technology Forum and Exposition, Online, 11–21 January 2021. [Google Scholar] [CrossRef]
- Xiong, K.; Zhang, Y.H.; Chan, W.C. Performance Evaluation of UKF-based Nonlinear Filtering. Automatica 2006, 42, 261–270. [Google Scholar] [CrossRef]
- Padulo, M.; Campobasso, S.M.; Guenov, D.M. Comparative Analysis of Uncertainty Propagation Methods for Robust Engineering Design. In Proceedings of the 16th International Conference on Engineering Design, ICED 2007, Paris, France, 28–31 July 2007. [Google Scholar]
- Shi, X.L.; Han, H.Z.; Shahbaz, M.; Song, P.W. Surrogate based Robust Airfoil Design under Aleatory Operating-conditions and Geometric Uncertainties. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Ghate, D.; Giles, M.B. Inexpensive Monte Carlo Uncertainty Analysis. Recent Trends in Aerospace Design and Optimization; Tata McGraw-Hill: New Delhi, India, 2006; pp. 203–210. [Google Scholar]
- Rumpfkeil, M.P.; Yamazaki, W.; Mavriplis, D.J. Uncertainty Analysis Utilizing Gradient and Hessian Information. In Proceedings of the 6th International Conference on Computational Fluid Dynamics, St. Petersburg, Russia, 12–16 July 2010; pp. 261–268. [Google Scholar] [CrossRef]
- Lockwood, B.A.; Rumpfkeil, M.P.; Yamazaki, W.; Mavriplis, D.J. Uncertainty Quantification in Viscous Hypersonic Flows using Gradient Information and Surrogate Modeling. In Proceedings of the 49th AIAA Aerospace Sciences Meeting, Orlando, FL, USA, 4–7 January 2011. [Google Scholar] [CrossRef]
- Yamazaki, W.; Mavriplis, D.J. Derivative-enhanced Variable Fidelity Surrogate Modeling for Aerodynamic Functions. AIAA J. 2013, 51, 126–137. [Google Scholar] [CrossRef]
- Rumpfkeil, M.P.; Hanazaki, K.; Beran, P. Construction of Multi-Fidelity Locally Optimized Surrogate Models for Uncertainty Quantification. In Proceedings of the 19th AIAA Non-Deterministic Approaches Conference, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Lee, K.H.; Park, G.J. A Global Robust Optimization Using Kriging Based Approximation Model. JSME Int. J. Ser. C 2006, 49, 779–788. [Google Scholar] [CrossRef]
- Lian, Y.; Kim, N.H. Reliability-Based Design Optimization of a Transonic Compressor. AIAA J. 2006, 44, 368–375. [Google Scholar] [CrossRef]
- Huang, Z.L.; Jiang, C.; Zhou, Y.S.; Zheng, J.; Long, X.Y. Reliability-based design optimization for problems with interval distribution parameters. Struct. Multidiscip. Optim. 2017, 55, 513–528. [Google Scholar] [CrossRef]
- Pisaroni, M.; Nobile, F.; Leyland, P. A Multilevel Monte Carlo Evolutionary Algorithm for Robust Aerodynamic Shape Design. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Quagliarella, D.; Iuliano, E. UQ Sensitivity Analysis and Robust Design Optimization of a Supersonic Natural Laminar Flow Wing-Body. Notes Numer. Fluid Mech. Multidiscip. Des. 2018, 140, 601–628. [Google Scholar] [CrossRef]
- Zhao, H.; Gao, Z.; Xu, F.; Zhang, Y. Review of Robust Aerodynamic Design Optimization for Air Vehicles. Arch. Comput. Methods Eng. 2019, 26, 685–732. [Google Scholar] [CrossRef]
- Schaefer, A.J.; Lazzara, S.D.; LeDoux, T.S. Robust Design of Sonic Boom Performance using Spatially Accurate Polynomial Chaos. In Proceedings of the 2023 AIAA Science and Technology Forum and Exposition (AIAA SciTech Forum), National Harbor, MD, USA, 23–27 January 2023. [Google Scholar] [CrossRef]
- Gelb, A.; Tadmor, E. Detection of Edges in Spectral Data. Appl. Comput. Harmon. Anal. 1999, 7, 101–135. [Google Scholar] [CrossRef]
- Gelb, A.; Tadmor, E. Detection of edges in spectral data II. Nonlinear enhancement. SIAM J. Numer. Anal. 2000, 38, 1389–1408. [Google Scholar] [CrossRef]
- Liem, R.P.; Mader, C.A.; Martins, J.R.R.A. Surrogate models and mixtures of experts in aerodynamic performance prediction for aircraft mission analysis. Aerosp. Sci. Technol. 2015, 43, 126–151. [Google Scholar] [CrossRef]
- Bettebghor, D.; Bartoli, N.; Grihon, S.; Morlier, J.; Samuelides, M. Surrogate modeling approximation using a mixture of experts based on EM joint estimation. Struct. Multidisc. Optim. 2011, 43, 243–259. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, H.; Zhou, C. A Study of Point Moving Adaptivity in Gridless Method. Comput. Meth. Appl. Mech. Eng. 2008, 197, 1926–1937. [Google Scholar] [CrossRef]
- Safian, K.; Yamazaki, W. Effect of Point Adaptation in Gridless CFD Method. In Proceedings of the 50th Aircraft Symposium, Niigata, Japan, 5–7 November 2012. JSASS-2012-5186. (In Japanese). [Google Scholar]
- Licher, R.M. Optimum Two-Dimensional Multiplanes in Supersonic Flow; Report No. SM-18688; Douglass Aircraft Co.: Santa Monica, CA, USA, 1955. [Google Scholar]
- Forrester, A.I.; Sobester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; Wiley: Chichester, UK, 2008. [Google Scholar] [CrossRef]
- Keane, J.A.; Voutchkov, I.I. Robust design optimization using surrogate models. J. Comput. Des. Eng. 2020, 7, 44–55. [Google Scholar] [CrossRef]
- Keane, J.A.; Voutchkov, I.I. Surrogate Approaches for Aerodynamic Section Performance Modeling. AIAA J. 2020, 58, 16–24. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Fleming, P.J. Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization. In Proceedings of the 5th International Conference on Genetic Algorithms, Urbana-Champaign, IL, USA, 17–21 July 1993; pp. 416–423. [Google Scholar]
- Kim, H.J.; Liou, M.S. New Multi-Objective Genetic Algorithms for Diversity and Convergence Enhancement. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Hupkens, I.; Deutz, A.; Yang, K.; Emmerich, M. Faster Exact Algorithms for Computing Expected Hypervolume Improvement. Evolutionary Multi-Criterion Optimization. Lect. Notes Comput. Sci. 2015, 9019, 65–79. [Google Scholar] [CrossRef]
- Hirose, K.; Yamazaki, W. Investigation of Reynolds Number Effect of Optimized Airfoil Shapes. In Proceedings of the 2022 Asia-Pacific International Symposium on Aerospace Technology, Niigata, Japan, 12–14 October 2022. S25-2. [Google Scholar]



















| Method | Cd | L/D | Computational Cost 1 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | ||||||
| MCS | 1.46 × 10−2 | 0% | 2.45 × 10−2 | 0% | 15.3 | 0% | 4.52 | 0% | 1000 |
| DDF | 2.10 × 10−2 | 44% | 3.22 × 10−2 | 31% | 14.4 | −6% | 5.89 | 30% | 3 |
| IMCS | 3.09 × 10−2 | 112% | 2.98 × 10−2 | 22% | 12.4 | −19% | 5.18 | 15% | 6 |
| divided IMCS (α = 0.1) | 1.45 × 10−2 | −1% | 2.44 × 10−2 | 0% | 15.3 | 0% | 4.48 | −1% | 8 |
| divided IMCS (α = 0.5) | 1.55 × 10−2 | 6% | 2.50 × 10−2 | 2% | 15.1 | −1% | 4.56 | 1% | 7 |
| divided IMCS (α = 1.0) | 1.79 × 10−2 | 22% | 2.89 × 10−2 | 18% | 14.1 | −8% | 5.00 | 11% | 6 |
| Airfoil Shape | Divided IMCS | MCS | IMCS’ | |||
|---|---|---|---|---|---|---|
| Mean of L/D | Std of L/D | Mean of L/D | Std of L/D | Mean of L/D | Std of L/D | |
| Busemann’s biplane | 14.1 | 5.00 | 15.3 | 4.52 | 15.2 | 4.59 |
| Design A | 15.0 | 0.0841 | - | - | 14.9 | 0.132 |
| Design B | 19.5 | 0.131 | - | - | 19.5 | 0.151 |
| Design C | 20.5 | 0.521 | - | - | 21.6 | 0.772 |
| Design D | 21.7 | 1.42 | - | - | 21.8 | 1.26 |
| Design E | 22.1 | 1.84 | - | - | 22.2 | 1.80 |
| Deterministic Optimal | 21.0 | 4.95 | - | - | 21.3 | 4.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanazaki, K.; Yamazaki, W. Robust Design Optimization of Supersonic Biplane Airfoil Using Efficient Uncertainty Analysis Method for Discontinuous Problem. Aerospace 2024, 11, 64. https://doi.org/10.3390/aerospace11010064
Hanazaki K, Yamazaki W. Robust Design Optimization of Supersonic Biplane Airfoil Using Efficient Uncertainty Analysis Method for Discontinuous Problem. Aerospace. 2024; 11(1):64. https://doi.org/10.3390/aerospace11010064
Chicago/Turabian StyleHanazaki, Kyohei, and Wataru Yamazaki. 2024. "Robust Design Optimization of Supersonic Biplane Airfoil Using Efficient Uncertainty Analysis Method for Discontinuous Problem" Aerospace 11, no. 1: 64. https://doi.org/10.3390/aerospace11010064
APA StyleHanazaki, K., & Yamazaki, W. (2024). Robust Design Optimization of Supersonic Biplane Airfoil Using Efficient Uncertainty Analysis Method for Discontinuous Problem. Aerospace, 11(1), 64. https://doi.org/10.3390/aerospace11010064