Flow Visualization around a Flapping-Wing Micro Air Vehicle in Free Flight Using Large-Scale PIV
Abstract
:1. Introduction
2. Materials and Methods
2.1. The DelFly MAV
2.2. The Flight Control System
2.3. The Particle Image Velocimetry (PIV) Procedure
3. Results and Discussion
3.1. Streamwise Planar Flow Visualizations
3.1.1. Results for the 45% Half-Span Visualization (S1)
3.1.2. Results for the 63% Half-Span Visualization (S2)
3.2. Analysis of the Flow-Induced Effect of the Flapping Wings
3.2.1. Estimation of Flow Conditions Perceived by the Tail
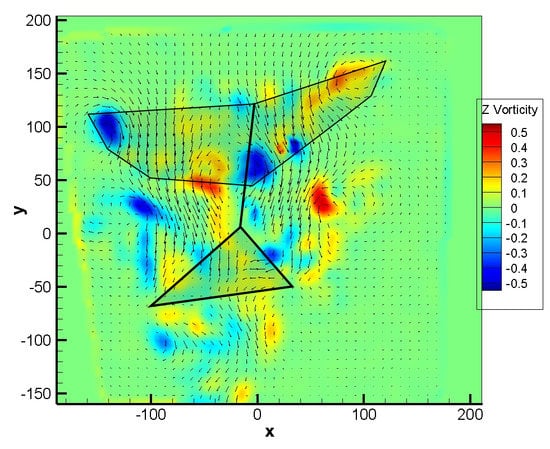
3.3. Spanwise Planar Flow Visualizations
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| FOV | Field of View |
| HFSB | Helium Filled Soap Bubbles |
| LEV | Leading Edge Vortex |
| MAV | Micro Air Vehicle |
| PIV | Particle Image Velocimetry |
| TEV | Trailing Edge Vortex |
References
- Wood, R.J. The first takeoff of a biologically inspired at-scale robotic insect. IEEE Trans. Robot. 2008, 24, 341–347. [Google Scholar] [CrossRef]
- Keennon, M.; Klingebiel, K.; Won, H.; Andriukov, A. Development of the nano hummingbird: A tailless flapping wing micro air vehicle. In Proceedings of the 50th AIAA Aerospace Sciences Meeting, Nashville, TN, USA, 9–12 January 2012. Paper AIAA 2012-0588. [Google Scholar] [CrossRef]
- de Croon, G.C.H.E.; Percin, M.; Remes, B.D.W.; Ruijsink, R.; de Wagter, C. The DelFly: Design, Aerodynamics, and Artificial Intelligence of a Flapping Wing Robot, 1st ed.; Springer: Heidelberg/Berlin, Germany, 2016; ISBN 978-94-017-9208-0. [Google Scholar]
- Ramezani, A.; Chung, S.-J.; Hutchinson, S. A biomimetic robotic platform to study flight specializations of bats. Sci. Robot. 2017, 2, eaal2505. [Google Scholar] [CrossRef]
- Sane, S.P. The aerodynamics of insect flight. J. Exp. Biol. 2003, 206, 4191–4208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, Q.V.; Truong, Q.T.; Park, H.C.; Goo, N.S.; Byun, D. Measurement of force produced by an insect-mimicking flapping-wing system. J. Bionic Eng. 2010, 7, 94–102. [Google Scholar] [CrossRef]
- Lin, C.-S.; Hwu, C.; Young, W.-B. The thrust and lift of an ornithopter’s membrane wings with simple flapping motion. Aerosp. Sci. Technol. 2006, 10, 111–119. [Google Scholar] [CrossRef]
- Lee, J.-S.; Han, J.-H. Experimental study on the flight dynamics of a bioinspired ornithopter: Free flight testing and wind-tunnel testing. Smart Mater. Struct. 2012, 21, 094023. [Google Scholar] [CrossRef]
- Percin, M.; van Oudheusden, B.; Eisma, H.; Remes, B. Three-dimensional vortex wake structure of a flapping-wing micro aerial vehicle in forward-flight configuration. Exp. Fluids 2014, 55, 1806. [Google Scholar] [CrossRef]
- Caetano, J.V.; Percin, M.; van Oudheusden, B.W.; Remes, B.; De Wagter, C.; de Croon, G.C.H.E.; de Visser, C.C. Error analysis and assessment of unsteady forces acting on a flapping wing micro air vehicle: Free flight versus wind-tunnel experimental methods. Bioinspir. Biomim. 2015, 10, 056004. [Google Scholar] [CrossRef] [PubMed]
- Johansson, L.C.; Hedenström, A. The vortex wake of blackcaps (Sylvia atricapilla L.) measured using high-speed digital particle image velocimetry (DPIV). J. Exp. Boil. 2009, 212, 3365–3376. [Google Scholar] [CrossRef] [PubMed]
- Hubel, T.Y.; Riskin, D.K.; Swartz, S.M.; Breuer, K.S. Wake structure and wing kinematics: The flight of the lesser dog-faced fruit bat, Cynopterus brachyotis. J. Exp. Boil. 2010, 213, 3427–3440. [Google Scholar] [CrossRef] [PubMed]
- Muijres, F.T.; Johansson, L.C.; Barfield, R.; Wolf, M.; Spedding, G.R.; Hedenström, A. Leading-edge vortex improves lift in slow-flying bats. Science 2008, 319, 1250–1253. [Google Scholar] [CrossRef] [PubMed]
- De Clercq, K.M.E.; de Kat, R.; Remes, B.; van Oudheusden, B.W.; Bijl, H. Aerodynamic experiments on DelFly II: Unsteady lift enhancement. Int. J. Micro Air Veh. 2009, 1, 255–262. [Google Scholar] [CrossRef]
- Percin, M.; van Oudheusden, B.W.; Remes, B. Flow structures around a flapping-wing micro air vehicle performing a clap-and-peel motion. AIAA J. 2017, 55, 1251–1264. [Google Scholar] [CrossRef]
- Deng, S.; van Oudheusden, B.W. Wake structure visualization of a flapping-wing micro-air-vehicle in forward flight. Aerosp. Sci. Technol. 2016, 50, 204–211. [Google Scholar] [CrossRef]
- Karasek, M.; Percin, M.; Cunis, T.; van Oudheusden, B.W.; De Wagter, C.; Remes, B.D.W.; de Croon, G.C.H.E. First free-flight flow visualisation of a flapping-wing robot. arXiv 2016, arXiv:1612.07645. [Google Scholar]
- Scarano, F.; Ghaemi, S.; Caridi, G.C.A.; Bosbach, J.; Dierksheide, U.; Sciacchitano, A. On the use of helium-filled soap bubbles for large-scale tomographic PIV in wind tunnel experiments. Exp. Fluids 2015, 56, 42. [Google Scholar] [CrossRef]
- Percin, M.; van Oudheusden, B.W.; de Croon, G.C.H.E.; Remes, B. Force generation and wing deformation characteristics of a flapping-wing micro air vehicle ‘DelFly II’ in hovering flight. Bioinspir. Biomim. 2016, 11, 036014. [Google Scholar] [CrossRef] [PubMed]
- Remes, B.D.W.; Esden-Tempski, P.; van Tienen, F.; Smeur, E.; De Wagter, C.; de Croon, G.C.H.E. Lisa-S 2.8g autopilot for GPS-based flight of MAVs. In Proceedings of the IMAV 2014: International Micro Air Vehicle Conference and Competition 2014, Delft, The Netherlands, 12 August 2014. [Google Scholar] [CrossRef]
- Armanini, S.F.; de Visser, C.C.; de Croon, G.; Caetano, J.V. Modelling wing wake and tail-wake interaction of a clap-and-peel flapping-wing MAV. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Denver, CO, USA, 5–9 June 2017. Paper AIAA 2017-0581. [Google Scholar] [CrossRef]
- Rijks, F.G.J.; Karásek, M.; Armanini, S.F.; de Visser, C.C. Studying the effect of the tail on the dynamics of a flapping-wing MAV using free-flight data. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Kissimmee, FL, USA, 8–12 January 2018. Paper AIAA 2018-0524. [Google Scholar] [CrossRef]
- Henningsson, P.; Michaelis, D.; Nakata, T.; Schanz, D.; Geisler, R.; Schröder, A.; Bomphrey, R.J. The complex aerodynamic footprint of desert locusts revealed by large-volume tomographic particle image velocimetry. J. R. Soc. Interface 2015, 12, 0119. [Google Scholar] [CrossRef] [PubMed]
- Martínez Gallar, B.; van Oudheusden, B.W.; Sciacchitano, A.; Karasek, M. Large-scale flow visualization of a flapping-wing micro air vehicle. In Proceedings of the 18th International Symposium on Flow Visualization, Zurich, Switzerland, 26–29 June 2018. [Google Scholar] [CrossRef]











| Cycle-Averaged U-Velocity | S1 | S2 | Cycle-Averaged V-Velocity | S1 | S2 |
|---|---|---|---|---|---|
| inlet | −0.92 m/s | −0.36 m/s | inlet | −0.05 m/s | −0.33 m/s |
| outlet | −0.45 m/s | −0.97 m/s | outlet | −2.64 m/s | −3.40 m/s |
| outlet-inlet | +0.47 m/s | −0.61 m/s | outlet-inlet | −2.59 m/s | −3.07 m/s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Estal Herrero, A.; Percin, M.; Karasek, M.; Van Oudheusden, B. Flow Visualization around a Flapping-Wing Micro Air Vehicle in Free Flight Using Large-Scale PIV. Aerospace 2018, 5, 99. https://doi.org/10.3390/aerospace5040099
Del Estal Herrero A, Percin M, Karasek M, Van Oudheusden B. Flow Visualization around a Flapping-Wing Micro Air Vehicle in Free Flight Using Large-Scale PIV. Aerospace. 2018; 5(4):99. https://doi.org/10.3390/aerospace5040099
Chicago/Turabian StyleDel Estal Herrero, Alejandro, Mustafa Percin, Matej Karasek, and Bas Van Oudheusden. 2018. "Flow Visualization around a Flapping-Wing Micro Air Vehicle in Free Flight Using Large-Scale PIV" Aerospace 5, no. 4: 99. https://doi.org/10.3390/aerospace5040099
APA StyleDel Estal Herrero, A., Percin, M., Karasek, M., & Van Oudheusden, B. (2018). Flow Visualization around a Flapping-Wing Micro Air Vehicle in Free Flight Using Large-Scale PIV. Aerospace, 5(4), 99. https://doi.org/10.3390/aerospace5040099