Parametric Modeling of a Long-Range Aircraft under Consideration of Engine-Wing Integration †
Abstract
:1. Introduction
2. Materials, Methods, and Tools
2.1. Aircraft Configurations
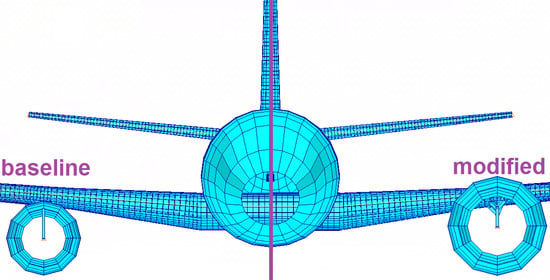
2.1.1. Reference Aircraft Configuration
2.1.2. Modified Aircraft Configuration
2.2. Parametric Modeling
2.2.1. The Basic MONA Process
2.2.2. The Automatized cpacs-MONA Process
2.2.3. Parameterized Engine-Wing Integration
2.3. Flutter Analysis
3. Results
3.1. Resulting Flight Load Distribution
3.2. Resulting Wing Thickness Distribution
3.3. Results on the Flutter Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | Institute of Aeroelasticity |
| AIC | Aerodynamic influence coefficient |
| CAD | Computer-aided design |
| CG | Center of gravity |
| CPACS | Common Parametric Aircraft Configuration Schema |
| CS-25 | Certification specifications for large airplanes |
| CWB | Center wing-box |
| DLM | Doublet lattice method |
| DLR | German Aerospace Center / Deutsches Zentrum für Luft und Raumfahrt |
| EAS | Equivalent airspeed |
| GFEM | Global finite element model |
| HTP | Horizontal tail-plane |
| LE | Leading edge |
| LRA | Loads reference axis |
| MDO | Multidisciplinary Design Optimisation |
| MTOM | Maximum take-off mass |
| MZFM | Maximum zero-fuel mass |
| neo | New engine option |
| OME | Operating mass empty |
| PCS | Preliminary cross-section sizing |
| RBE2 | Rigid Body Element No.2 |
| UAV | Unmanned aerial vehicle |
| VCT | Vortex carry through |
| VLM | Vortex lattice method |
References
- Kellari, D.; Crawley, E.F.; Cameron, B.G. Influence of Technology Trends on Future Aircraft Architecture. J. Aircr. 2017, 54, 2213–2227. [Google Scholar] [CrossRef] [Green Version]
- Cumnuantip, S. Landing Gear Positioning and Structural Mass Optimization for a Large Blended Wing Body Aircraft. Ph.D. Thesis, DLR-Forschungsbericht, Goettingen, Germany, July 2014. [Google Scholar]
- Chai, S.T.; Mason, W.H. Landing Gear Integration in Aircraft Conceptual Design; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 1997. [Google Scholar]
- Li, J.; Gao, Z.; Huang, J.; Zhao, K. Aerodynamic design optimization of nacelle/pylon position on an aircraft. Chin. J. Aeronaut. 2013, 26, 850–857. [Google Scholar] [CrossRef] [Green Version]
- Guenot, D.; Gallard, F.; Brezillon, J.; Merillac, Y. Aerodynamic optimization of a parametrized engine pylon on a mission path using adjoint method. In Proceedings of the 7th European Conference on Computational Fluid Dynamics, Glasgow, UK, 11–15 June 2018. [Google Scholar]
- Wang, L.; Wan, Z.; Wu, Q.; Yang, C. Aeroelastic modeling and analysis of the wing/engine system of a large aircraft. Procedia Eng. 2012, 31, 879–885. [Google Scholar] [CrossRef] [Green Version]
- Latif, R.; Khan, M.; Javed, A.; Shah, S.; Rizvi, S. A semi-analytical approach for flutter analysis of a high-aspect-ratio wing. Aeronaut. J. 2020, 1–20. [Google Scholar] [CrossRef]
- Amoozgar, M.; Irani, S.; Vio, G. Aeroelastic instability of a composite wing with a powered-engine. J. Fluids Struct. 2013, 36, 70–82. [Google Scholar] [CrossRef]
- Fazelzadeh, S.A.; Mazidi, A.; Kalantari, H. Bending-torsional flutter of wings with an attached mass subjected to a follower force. J. Sound Vib. 2009, 323, 148–162. [Google Scholar] [CrossRef]
- Mardanpour, P.; Hodges, D.H.; Neuhart, R.; Graybeal, N. Engine Placement Effect on Nonlinear Trim and Stability of Flying Wing Aircraft. J. Aircr. 2013, 50, 1716–1725. [Google Scholar] [CrossRef]
- Jonsson, E.; Mader, C.A.; Martins, J.R.R.A.; Kennedy, G.J. Computational modeling of flutter constraint for high-fidelity aerostructural optimization. In Proceedings of the AIAA SciTech Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Cavagna, L.; Ricci, S.; Travaglini, L. NeoCASS: An integrated tool for structural sizing, aeroelastic analysis and MDO at conceptual design level. Progress Aerosp. Sci. 2011, 47, 621–635. [Google Scholar] [CrossRef]
- Manzano, M.D.L.M.S. Studying Aeroelastic Behavior of Aircraft with NeoCASS. The Danbus Configuration, Stockholm: KTH Royal Institute of Technology; Department Aeronautical and Vehicle Engineering: Stockholm, Sweden, 2011. [Google Scholar]
- Waitz, S.; Hennings, H. The Aeroelastic Impact of Engine Thrust and Gyroscopics on Aircraft Flutter Instabilities; IFASD: Saint Petersburg, Russia, 2015. [Google Scholar]
- Pfeiffer, T.; Moerland, E.; Böhnke, D.; Nagel, B.; Gollnick, V. Aircraft Configuration Analysis Using a Low-Fidelity, Physics Based Aerospace Framework Under Uncertainty Considerations; International Council of the Aeronautical Sciences: Saint Petersburg, Russia, 2014. [Google Scholar]
- Moerland, E.; Siggel, M.; Kleinert, J. DLR-SC TIGL Testdata, CPACS Dataset D250. Available online: https://github.com/DLR-SC/tigl/blob/master/tests/unittests/TestData/CPACS_30_D250_10.xml (accessed on 15 December 2020).
- European Aviation Safety Agency. Type Certificate Data Sheets (TCDS) EASA.A.004-A330; European Aviation Safety Agency: Cologne, Germany, 10 September 2020; Available online: https://www.easa.europa.eu/sites/default/files/dfu/A330EASACDSA.004-Issue58-Core.pdf (accessed on 9 November 2020).
- European Aviation Safety Agency. Type Certificate Data Sheets (TCDS) EASA.E.042-Trent 700 Series Engines; European Aviation Safety Agency: Cologne, Germany, 20 December 2019; Available online: https://www.easa.europa.eu/sites/default/files/dfu/EASAE042TCDSissue06_Trent700.pdf (accessed on 9 November 2020).
- European Aviation Safety Agency. Type Certificate Data Sheets (TCDS) EASA.E.036-Trent 1000 Series Engines; EASA: Cologne, Germany, 20 July 2018; Available online: https://www.easa.europa.eu/sites/default/files/dfu/TCDSE036issue10.pdf (accessed on 9 November 2020).
- Rolls-Royce, Future Products-UltraFan. Available online: https://www.rolls-royce.com/products-and-services/civil-aerospace/future-products.aspx#section-overview (accessed on 8 December 2020).
- Clean Sky, The UHBR Engine Flight Testing Programme Gathers Momentum. 2020. Available online: https://www.cleansky.eu/the-uhbr-engine-flight-testing-programme-gathers-momentum (accessed on 9 December 2020).
- Klimmek, T.; Schulze, M.; Abu-Zurayk, M.; Ilic, C.; Merle, A. cpacs-MONA–An Independent and in High-Fidelity Based MDO Tasks Integrated Process for the Structural and Aeroelastic Design of Aircraft Configurations; IFASD: Savannah, GA, USA, 2019. [Google Scholar]
- Klimmek, T. Parametrization of Topology and Geometry for the Multidisciplinary Optimization of Wing Structures. In Proceedings of the European Air and Space Conference, Manchester, UK, 26–29 October 2009. [Google Scholar]
- MSC Software Corporation. MSC Nastran 2017 Quick Reference Guide; MSC Software: Newport Beach, CA, USA, 2016. [Google Scholar]
- Klimmek, T. Statische Aeroelastische Anforderungen Beim Multidiszipliären Strukturentwurf von Verkehrsflugzeugen. Ph.D. Thesis, German Aerospace Center, Goettingen, Germany, 2016. [Google Scholar]
- Merle, A.; Ilic, C.; Abu-Zurayk, M.; Häßy, J.; Becker, R.-G.; Schulze, M.; Klimmek, T. High-Fidelity Adjoint-based Aircraft Shape Optimization with Aeroelastic Trimming and Engine Coupling; EUROGEN: Guimarães, Portugal, September 2019. [Google Scholar]
- Abu-Zurayk, M.; Merle, A.; Caslav, I.; Goertz, S.; Schulze, M.; Klimmek, T. A Comparison of Different Formulations for Aero-Structural Optimization of Trimmed Transport Aircraft; EUROGEN: Guimarães, Portugal, 2019. [Google Scholar]
- Görtz, S.; Ilic, C.; Jepsen, J.; Leitner, M.; Schulze, M.; Schuster, A.; Scherer, J.; Becker, R.-G.; Zur, S.; Petsch, M. Multi-Level MDO of a Long-Range Transport Aircraft Using a Distributed Analysis Framework; AIAA: Denver, CO, USA, 2017. [Google Scholar]
- Nagel, B.; Böhnke, D.; Gollnick, V.; Schmollgruber, P.; Rizzi, A.; la Rocca, G.; Alonso, J.J. Communication in aircraft design: Can we establish a common language? In Proceedings of the ICAS, 28th International Congress of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012. [Google Scholar]
- MSC Software. MSC Nastran 2017 Aeroelastic Analysis User’s Guide; MSC Software: Newport Beach, CA, USA, 2016. [Google Scholar]
- MSC Software. MSC Nastran 2017 Design Sensitivity and Optimization User’s Guide; MSC Software: Newport Beach, CA, USA, 2016. [Google Scholar]
- Chiozzotto, G.P. CDloads: Conceptual Design Loads Estimation; DLR-Institute of Aeroelastcity: Goettingen, Germany, 2013. [Google Scholar]
- Van Dalen, F. MDO Load Analysis and Preliminary Sizing; Delft University of Technology: Delft, The Netherlands, December 1996. [Google Scholar]
- Federal Aviation Administration. Federal Aviation Regulations Part 25 C; Airworthiness Standards: Transport Category Airplanes; Federal Aviation Administration (FAA): Washington, DC, USA, 2010. [Google Scholar]
- Guyan, R.J. Reduction of stiffness and mass matrices. AIAA J. 1965, 3, 380. [Google Scholar] [CrossRef]
- Hedman, S.G. Vortex Lattice Method for Calculation of Quasi Steady State Loadings on Thin Elastic Wings; Technical Report 105; FFA—The Aeronautical Institute of Sweden: Stockholm, Sweden, 1966. [Google Scholar]
- Albano, E.; Rodden, W.P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. AIAA J. 1969, 7, 279–285. [Google Scholar] [CrossRef]
- ZONA Technology, Inc. ZAERO User’s Manual Version 9.2, 3rd ed.; ZONA Technology, Inc.: Scottsdale, AZ, USA, 2017. [Google Scholar]
- Chen, P. Damping Perturbation Method for Flutter Solution: The g-Method. AIAA J. 2000, 38, 1519–1524. [Google Scholar] [CrossRef]
- ZONA Technology, Inc. ZAERO Theroetical Manual Version 9.2, 3rd ed.; ZONA Technology, Inc.: Scottsdale, AZ, USA, 2018. [Google Scholar]

















| A/C Characteristic | Value | Units |
|---|---|---|
| Span | 58 | m |
| Wing area | 362 | m2 |
| Aspect ratio | 9.3 | - |
| LE sweep | 32 | deg. |
| Reference chord | 6.23 | m |
| MTOM | 230 | t |
| OEM | 111 | t |
| Engine Parameter | Baseline | Modified |
|---|---|---|
| Outer diameter | 3.0 m | 4.0 m |
| Mass | 6150 kg | 7000 kg |
| x-position (CG) | 21.6 m | 20.6 m |
| z-position (CG) | −2.6 m | −2.1m |
| Length | 5.64 m | 6.0 m |
| Mass Case | Design Mass | Payload | Fuel |
|---|---|---|---|
| MOOee | OME | 0% | 0% |
| MTOAa | MTOM | 100% | 83% |
| MTOfF | MTOM | 63% | 100% |
| MZOAe | MZFM | 100% | 0% |
| MFOeF | “delivery” | 0% | 100% |
| Pylon Parameter | Baseline | Modified |
|---|---|---|
| PARH1 | 0.6 | 0.6 |
| PARH2 | 0.3 | 0.3 |
| DIM3 and DIM4 | 0.02 m | 0.025 m |
| DIM5 and DIM6 | 0.02 m | 0.025 m |
| PB1_P-W and PB2_P-W | 0.12 m | 0.15 m |
| Mass Case | Flutter Speed (EAS) | Mode No. | Frequency |
|---|---|---|---|
| MTOfF | - | - | - |
| MOOee | 306.5 m/s | 18 | 10.2 Hz |
| MZOAe | 307.0 m/s | 18 | 10.2 Hz |
| MFOeF | 315.6 m/s | 19 | 10.5 Hz |
| MTOAa | 340.3 m/s | 21 | 11.0 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schulze, M.; Neumann, J.; Klimmek, T. Parametric Modeling of a Long-Range Aircraft under Consideration of Engine-Wing Integration. Aerospace 2021, 8, 2. https://doi.org/10.3390/aerospace8010002
Schulze M, Neumann J, Klimmek T. Parametric Modeling of a Long-Range Aircraft under Consideration of Engine-Wing Integration. Aerospace. 2021; 8(1):2. https://doi.org/10.3390/aerospace8010002
Chicago/Turabian StyleSchulze, Matthias, Jens Neumann, and Thomas Klimmek. 2021. "Parametric Modeling of a Long-Range Aircraft under Consideration of Engine-Wing Integration" Aerospace 8, no. 1: 2. https://doi.org/10.3390/aerospace8010002
APA StyleSchulze, M., Neumann, J., & Klimmek, T. (2021). Parametric Modeling of a Long-Range Aircraft under Consideration of Engine-Wing Integration. Aerospace, 8(1), 2. https://doi.org/10.3390/aerospace8010002