1. Introduction
With the development of aerospace technology, human activities in space are becoming more frequent. The space debris left by human beings in space, especially in the Earth’s orbit, is increasing at a tremendous rate because of the rapid deployment of large scale low earth orbit constellations, such as the plan of more than 20,000 satellites proposed by two dozen companies [
1]. Space debris mainly consists of abandoned satellites, rocket final stage devices and collision debris [
2]. According to the results of computer simulation, even if we were to stop all space activities and comply with the 25-year removal guidelines, the amount of space debris will continue to grow, and the density of space debris will increase as well due to random collisions. This transitive phenomenon is called the “Kessler phenomenon” [
3]. Actively removing orbital debris is the only feasible solution to control the spread of debris in the future.
Unlike satellites that operate stably in orbit, the motion state of space debris is irregular and it is likely that there is a large residual angular momentum due to passivation, collision, environmental torque, etc. Existing contact debris despinning technologies such as flexible brush [
4,
5], mechanical pulse [
6], space manipulator technology or deceleration brush despinning technology relying on manipulators [
7] require a relatively static situation between the service satellite and the target. This requires extremely high accuracy in modeling and control and is prone to collision risks. For irregular targets that rotate at high speed, there is no way to make safe contact. However, the more researched space rope net method [
8] also has unsafe factors such as excessive force at the moment of contact. Non-contact despinning technology is a hot topic that has emerged in recent years. Its application methods include the compressed gas method [
9], ion beam method [
10,
11], electrostatic force method [
12] and laser ablation method [
13,
14] and other new concepts and methods. Electricity, magnetism or jet-flow are usually adopted to generate despinning torque. Since there is no direct contact, the magnitude of the despinning torque is usually small, at the level of mN·m. Therefore, the target has little impact on the service satellite and robotic arm during the process of despinning and the time required is usually at the level of hundreds of hours. During this period, the position and attitude accuracy requirements are low, and the effective working distance has a large range of variation. In order to overcome the shortcomings of the existing contact and non-contact despinning technologies, it is necessary to seek a more effective non-contact despinning method.
Electromagnetic eddy current despinning is a method of despinning based on the electromagnetic eddy current damping effect. It is a non-contact depinning method that uses the damping moment generated by the rotating conductor to cut the magnetic line of induction in an artificial magnetic field. This torque is also called the eddy current torque. The earliest systematic study of eddy current torque came from NASA’s study on the rotation characteristics of a near-Earth satellite in the Earth’s magnetic field in 1965 [
15]. It was the first work to put forward the inherent characteristics of conductors-the concept of electromagnetic tensor, and give the eddy current torque expression. Due to the weak geomagnetic effect, the ultimate research goal was to explore the long-term effect of the average eddy current induced by the geomagnetism on the satellite. Later, researchers mostly carried out research and experiments on the basis of this theoretical model. The concept of eddy current despinning was formally proposed in the 1980s. Scientists conducted more in-depth research on the eddy current torque generated by rotating magnets induced by artificial electromagnetic fields. In 1995, the American scientist Kadaba [
16] conducted an engineering feasibility study on eddy current despinning for spacecrft, and proposed an electromagnetic eddy current despinning scheme based on high-temperature superconducting coils.
In the past decade, the need for space debris removal has become increasingly urgent, and new concepts including electromagnetic eddy current despinning methods have once again become research hotspots. Sugai studied an electromagnetic brake system based on a robotic arm [
17], using a smart robotic arm to carry electromagnetic brake pads close to the target surface for damping braking, which is similar to the method of the robot arm decelerating brush proposed by the Japan Aerospace Agency in 2006 [
7]. In 2019, Xie et al. designed new permanent magnet array brake pads and dual manipulator structure and established dynamic model further verifying the effectiveness of this approach [
18]. However, the distance between the eddy current brake and the target is limited to a very small range in above method, which cannot really solve the collision safety problem of contact despinning. In 2015, Ortiz Gómez et al. at the University of Southampton used Ariane H10 final stage despinning as an application scenario, focusing on explaining the mechanism of eddy current depinning [
19,
20]. and they constructed a standardized eddy current force and eddy current torque model. In 2019, Liu et al. conducted dynamic modeling for eddy current brake in three-dimensional environment on the basis of existing researches, and designed nonlinear sliding model controller, which further verified the feasibility of eddy current despinning technology [
21]. However, the existing eddy current despinning technology still relies on the thrust device of the service satellite to maintain the relative position, which often lasts as long as several days. Moreover, the efficiency depends on the target speed. When the target speed drops, the despinning efficiency will be significantly reduced. The above problems greatly limit the application process of eddy current despinning technology. In order to break through the bottleneck of the application of eddy current despinning technology, this paper develop a non-propellant eddy current despinning and traction technology based on magnetic pulses. Compared with [
19,
20,
21], the proposed method makes the despinning process get rid of the propellant limitation, and enables the target speed to decrease steadily.
This article is outlined as follows. In the second section, the article introduces the technical details of the non-propellant eddy current brake and traction technology based on magnetic pulse, including basic theory (
Section 2.1), device design (
Section 2.2), analysis method (
Section 2.3) And control strategy (
Section 2.4). In the third section, the simulation results of this technology are shown. The effectiveness and superiority of the technology proposed in this paper are proved from three aspects of control strategy (
Section 3.1), efficiency (
Section 3.2) and traction control effect (
Section 3.3).
2. Non-Propellant Eddy Current Brake and Traction Using Magnetic Pulse
In this section, non-propellant eddy current brake and traction technology based on magnetic pulse is introduced in detail. Firstly, the origin of the concept of non-propellant eddy current brake is explained. Secondly, according to the key technical details, an overall plan to realize the technology is designed and the model is simplified in order to analyze the technical principles. Finally, a unique magnetic pulse control method is proposed.
2.1. Basic Theory
Natalia Ortiz Gómez et al. analyzed the mechanism of eddy current despinning in detail in [
19,
20], and studied the traction problem under the conventional mode. According to the derivation results in the literature, the object rotating in a fixed magnetic field can be damped by the eddy current torque
T. The eddy current torque calculation equation is shown as follows:
where,
w is the relative rotation angular velocity vector between the target and serving satellite,
M is the electromagnetic tensor of the target, which is the inherent electromagnetic property of the conductor target, determined by the material and structure of the conductor. The target selected in this paper is a metal spherical shell, and its electromagnetic tensor is:
where,
M is the third-order diagonal matrix,
E third-order unit matrix,
σt is the conductivity of the target conductive material,
Rt is the radius of the spherical shell,
et is the thickness of the spherical shell.
μeff is the effective factor of non-uniform magnetic field, used to correct the eddy current torque error caused by non-uniform magnetic field.
The object rotating in a fixed magnetic field is also affected by the eddy current force
F, so that the angular momentum conservation of the system can be satisfied. The eddy current force calculation equation is shown as follows:
where,
ΛGt represents the Jacobian matrix of the magnetic field, the matrix equation is shown as follows:
where,
m is the magnetic moment of the coil,
μ0 is permeability of vacuum,
r is the distance between target and service satellite.
2.2. Device Design
This section first analyzes the principle of the conventional eddy current despinning method. Then, in order to further improve the efficiency and reduce propellant consumption, we proposed the concept of eddy current despinning and traction based on a variable magnetic field. Finally, a new device was designed according to the requirements.
The conventional eddy current despinning mode is shown in
Figure 1. The service satellite applies a constant magnetic field to the target, so that the target is subject to eddy current damping torque. Eddy current forces are generated at the same time, satisfying the angular momentum conservation. However, the eddy current force generated by the coupling of the target angular velocity and the applied magnetic field is regarded as a non-linear interference and needs to be offset by the attitude orbit controller of the service satellite.
According to Equation (3), the eddy current force is mainly controlled by the relative angular velocity and magnetic field strength. The relative angular velocity is essentially the angular velocity of the target relative to the static magnetic field. When the magnetic field is variable, the relative angular velocity is determined by the angular velocity of the target and the angular velocity of the magnetic field. As long as the hardware conditions permit, the variable magnetic field is able to dominate the direction and magnitude of the target eddy current force, achieving arbitrary control of the target.
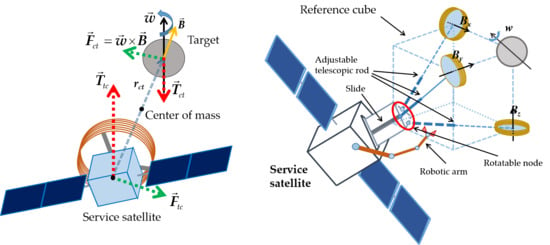
Figure 2 shows our newly designed despinning device. According to the concept of eddy current brake using variable magnetic field, the despinning device needs to be equipped with at least three non-coplanar magnetic field generators to meet the needs of generating arbitrary magnetic fields. In order to make the distance between the satellite and the target adjustable, the despinning device needs to have a telescopic structure. Due to the application of superconducting technology, light and heat shielding needs to be designed for the magnetic generators, thereby reducing the power consumption of the satellite. In addition, the storage, transportation and launch of satellites need to meet actual conditions, and the despinning device should also have a foldable design. It can maintain the folded state during the storage, transportation and launch stages, enhancing the structural strength.
The electromagnetic coil structure in the
Figure 2 is able to generate any magnetic field at the target. The coil realizes the adjustment of the working range and the storage function through the adjustable telescopic rod. The triangular column structure in the picture can be retracted into the satellite star. The rotation nodes on the cylinder work with the slide rails together so that the coil structure can also be incorporated into the satellite star during launch.
Figure 3 shows the fully folded service star structure.
In addition, the coil structure should also be specially treated as shown in
Figure 4 so as to better shield the light and heat interference.
Located in the center of the connecting rod in the
Figure 4 is the superconducting cable and the coolant channel. The wire is gray, and the coolant path and loop are green and blue respectively. The black part of the primary connecting rod is the supporting structure of the connecting rod, including the column core and the column shell. The thicker black part of the secondary connecting rod is the column shell, and the primary connecting rod is wrapped in the middle. The brown part of the connecting rod section in the picture and the blue outer cover of the coil are light and heat shielding layers.
2.3. Model Simplified Analysis
2.3.1. Simplification of Satellite Model
Simplifying the problem in the three-dimensional space to the two-dimensional plane for research is a common problem analysis strategy. This section simplifies the despinning problem and mechanism, as shown in
Figure 5.
The service satellite has two connecting rods and magnetic field generators placed perpendicular to each other, which can generate a magnetic field of any size and direction in the
xOy plane at the target. The target rotation axis is always parallel to the z-axis direction. According to Equation (3), it can be seen that the eddy current force on the target is in the
xOy plane. When the eddy current force
F is given, it is not difficult to find from
Figure 6 that the magnetic field needs to rotate in a specific direction at a specific angular velocity to meet the control requirements according to Equation (3). The magnetic field at this time is a variable periodic function, and the period is Δ
Ti.
The magnetic field components in each direction have the following mathematical expressions:
where:
2.3.2. Simplification of Superconducting Coil Loop
The last section gives the expression form of the ideal magnetic field, and the period Δ
Ti under ideal conditions can be infinitely small. In reality, charging and discharging of the inductance is limited because of the inductive reactance of the magnetic field generators. The expression of the ideal magnetic field in Equation (5) needs to be corrected to Equation (7):
where:
where,
kτwBi represents the angular displacement in
k times the charge and discharge time,
τ is the time constant of the charge and discharge when the total magnetic pulse is generated, and
wBi is the angular velocity of the magnetic field. As shown in
Figure 7, the width of pulse needs to meet the charging and discharging time of the coil, and the angle width of pulse
θ should not exceed a certain radian. Therefore, it is necessary to further study the exact relationship between
wBi and the charge-discharge time constant
τ.In the simplified model, the magnetic fields in each direction can be linearly superimposed, so it is better to study the charge and discharge characteristics of a single circuit first.
Figure 8 shows a simple loop with a single coil.
In the figure, R is the high-current resistance connected in series, L is the superconducting coil, E is the power supply voltage drop, i represents the current. According to existing material data, the working resistance of the superconducting coil is 10−24 Ω/cm, which can be negligible compared to the 1 Ω resistance connected in series. In other words, the superconducting coil in the loop can be simplified as an ideal inductance.
According to the current characteristics of the inductor:
Solving Equation (9), we can get:
where, the coil inductance
Ln can be approximated by the following equation:
where,
k is the Nagaoka coefficient,
S is the cross-sectional area of the coil,
N is the number of turns, and
l is the length of the coil.
Here we take the
x-axis as an example to study the charging and discharging process of the magnetic pulse so as to draw conclusions about Δ
Ti and
τ. First, the derivative of Equation (1) in Equation (8) is obtained as follows:
so:
Then we take the derivative of the current equation in the
x direction in Equation (10):
where,
E is the power supply voltage, and can be changed freely in range [−
Em,
Em]. Because of
, there is the following equation relationship:
where,
CB is the constant coefficient. It’s necessary to make the actual magnetic field to keep up with ideal magnetic field, the following inequality can be obtained:
With further simplification:
Equation (19) gives the limiting condition of the control period Δ
Ti. The charge and discharge time constant of the total magnetic pulse is set as follows:
In the process of selecting magnetic pulse parameters, the angular velocity wBi of the magnetic field needs to meet the constraints of Equation (19). The charging and discharging time constant τ of the total magnetic pulse satisfies Equation (20). The k in Equation (8) can be adjusted according to the pulse width, so that the angular displacement of the magnetic field vector Bi in a period meets the control requirements of traction.
2.4. Control Method Design
2.4.1. Control Strategy
The core of the magnetic pulse control technology is the variable pulse magnetic field described in
Section 2.3.1. In order to obtain the control signal used to resolve the electromagnetic pulse, the system introduces Equation (21), called the reference dynamic Equation [
20], achieving reference state
rref, as shown in
Figure 9.
The reference state is used to generate the reference control signal
Fref, which forms an open-loop control system. In order to suppress the divergence of the system, the state output
r of the dynamic Equation is differentiated from the reference state
rref and the result is introduced into control signals, forming a feedback control loop. The reference control signal
Fref and the feedback control signal
Ffb together form a continuous signal for magnetic pulse calculation. The original control signal is a continuous and needs to be discretized. Different from the conventional discretization method, we propose a method based on momentum, which is introduced in detail in
Section 2.4.2:
In addition, after the system converges, the eddy current control force is greatly reduced, and the eddy current torque will also decrease simultaneously, which reduces the despinning efficiency. In order to avoid the reduction of the efficiency, the eddy current torque enhancement module is specially introduced and designed. By imposing periodic disturbance on the state of the observer, the eddy current torque is always maintained at an effective value, which can be verified later:
where,
A represents the interference amplitude, and
w represents the angular velocity of the sinusoidal interference signal.
2.4.2. Discretization Method of Continuous Control Signal
As shown in
Figure 6, due to the uniqueness of the eddy current force form, conventional control ideas cannot be used directly here. It is not difficult to find that the instantaneous eddy current force has a certain periodic nature. The eddy current force at a certain moment can be regarded as a pulse in a variable period Δ
Ti, where Δ
Ti = 2
π/
wi. Since the target sways slightly near the predetermined position in the actual control process, there is no harm using the impulse within a variable period Δ
Ti to characterize the control effect of the object. In order to facilitate the derivation and expression of the control force, it is stipulated that the calculation range of the impulse received by the target is a circle. that is, the time for a magnetic field to scan the target is Δ
Ti, and the total impulse received by the target during this period is calculated.
The curve of impulse, reduced impulse and equivalent impulse with respect to position after unfolding the target circle in the unit of circumference is shown in
Figure 10. The left side of the picture is the actual demonstration diagram, and the right side is the schematic diagram of the circle expansion. The curve in the first coordinate system shows the distribution of impulse within Δ
Ti of the applied control force at different positions in the unit of circle. The curve in the second coordinate system represents the impulse distribution curve at the position where the remaining impulse is positive after the impulse in the opposite direction is offset. The curve in the third coordinate system represents the equivalent impulse of the vector sum of the impulses in Δ
Ti, and the impulse pulse width is determined according to the coil inductance model parameters in
Section 2.3.2.
It should be noted that the concept of equivalent impulse in ΔTi is based on the assumption that ΔTi is small enough and the target displacement within the variable period is small.
2.4.3. Solution of Magnetic Pulse Signal
The first step of magnetic pulse control is to find the control force at any time, and then through the discretization, the relative angular velocity
w and the central magnetic field
BGt can be inversely solved by Equation (3). As shown in
Figure 11, the result of the inverse solution is not unique. Therefore, the solution rules need to be appointed.
In the two-dimensional plane model, the magnetic angular velocity required in Result 1 is much smaller than that in Result 2. A larger magnetic angular velocity may increase the difficulty of controlling the magnetic field generator. In addition, the eddy current torque in result 1 is opposite to the target speed, which plays a role of braking. The eddy current torque in result 2 is in the same direction as the target speed, which accelerates the target’s rotation speed. Therefore, when solving Equation (3), it is necessary to make the applied magnetic field speed as small as possible and the eddy current torque along the opposite direction of the target angular velocity as much as possible, which must be taken as the criterion.
4. Conclusions
This paper studies the despinning method of the space rotating target, proposes a method of despinning and traction based on magnetic pulse without propellant, and designs a new despinning device. In order to realize the proposed despinning and traction method, a discretization method of control signal based on momentum model is studied in this paper. This method grasps the relatively static characteristics of the formation between the active and passive sides and discretizes the continuous control signal by calculating the total impulse of the eddy current force in a small period. Then, the simplified inductance model is used to derive the magnetic pulse in the two-dimensional simplified model, obtaining constraints on key parameters such as the electromagnetic pulse period ΔTi. In addition, an eddy current torque enhancement module that uses periodic interference signals is designed so as to solve the problem of the despinning torque disappearing in the steady state of the system.
According to the simulation results, the discretization method based on momentum model proposed in this paper doesn’t affect the control stability of the system under the limitation of electromagnetic pulse parameters. By comparing the changes of the target angular velocity before and after the introduction of the eddy current torque enhancement module, it is not difficult to find that the eddy current torque enhancement module introduced in this paper really solve the problem of the torque disappearing in the steady state. What’s more, the efficiency of the conventional eddy current despinning method decrease with the decrease of the target speed, and it is necessary to consume propellant for a long time to maintain the formation. The eddy current despinning and traction method based on magnetic pulse does not need propellant, and the efficiency is not affected by the target state. Compared with conventional methods, the method proposed in this paper has certain advantages. Apart from the field of despinning, this technology can also be applied to the field of passive traction of space targets, etc. The theoretical research and numerical experimental data in this paper can provide an effective reference for the development of related fields.