1. Introduction
In response to the challenges of airspace congestion, flight delays, and other challenges brought about by increasing traffic volumes to improve the level of safety, efficiency, and sustainability of the air traffic system, Europe launched the Single European Air ATM Study (SESAR), the United States launched the Next Generation Air Transport System (NextGen), the International Civil Aviation Organization (ICAO) built the Aviation System Block Upgrade (ASBU) framework, etc. One of the common key technologies to all these automated systems is the ability to analyze and process large numbers of trajectory records scientifically and efficiently. The reason is that historical trajectory data contains a lot of potentially useful information. At present, the most commonly used and efficient method to mine potential information from a large amount of trajectory data is to perform clustering analysis on trajectories. Through clustering analysis, the frequent flight patterns of aircraft, air traffic flow situation, airspace usage, etc. can be known, which can reflect the flight tendency of aircraft and the control habits of controllers to a certain extent. It can provide a reference for the optimization of the division of airspace sectors and for the controller to make control decisions. In addition, many scholars regard trajectory clustering as one of the key steps in trajectory prediction. By classifying similar trajectories into one category in advance, and then establishing a prediction model for each category of trajectories separately, the prediction results can be more accurate and robust [
1,
2].
Trajectory clustering methods can be roughly divided into four categories, including clustering based on the partition, density, grid, and probability models. All of these clustering methods can be used to cluster the trajectories and can achieve certain results. Among the partition-based clustering methods, the K-means clustering algorithm has higher computational efficiency than other algorithms and does not need to spend a lot of time debugging parameters. The only parameter that needs to be input is the number of clusters, which has the advantage of being easy to implement. Therefore, it is adopted by most scholars [
3,
4,
5,
6,
7,
8]. Barrat et al. [
7] used K-means to acquire the center trajectories, and then constructed a Gaussian mixture model based on the center trajectories to achieve accurate inference and generate more realistic trajectories. Ayhan et al. [
6] considered that treating a trajectory as a whole may lead to overfitting, and cannot find representative trajectories, so they proposed a clustering framework of aircraft trajectories based on the tasks of division, clustering, and merging. Use a set of multi-dimensional trajectory points associated with a particular flight, divide them according to flight phase, cluster them individually with the K-means algorithm, and combine them. In addition, in contrast, the K-medoids algorithm, in addition to being relatively slow, selects centers from the actual data points within the cluster. Therefore, it is not sensitive to outliers [
9,
10]. Kenefic et al. [
10] adopted the K-medoids algorithm based on the minimum description length and the Frechet distance, which can be generalized to the clustering problem of datasets with arbitrary shapes.
The most popular method in density-based clustering is Density-Based Spatial Clustering of Applications with Noise (DBSCAN). Most density-based trajectory clustering is implemented by the DBSCAN algorithm or improved implementation of the algorithm [
11,
12,
13,
14]. Olive et al. [
12] first used the DBSCAN algorithm to identify the initial set of clusters and outliers, and then adopted the progressive clustering method. For the classes that cannot be well separated, the clusters were refined by applying the DBSCAN algorithm to each flow again. Verdonk et al. [
13] proposed an algorithm RDBSCAN based on the recursive application of DBSCAN, which recursively creates a hierarchy that enables a more customized classification of outliers. Hierarchical clustering creates a hierarchical decomposition of a given set of objects. Depending on how the hierarchical decomposition is formed, hierarchical methods can be classified as agglomerative or divisive methods [
15,
16,
17]. Zhang et al. [
16] introduced an agglomerative hierarchical clustering method that builds a hierarchical structure based on a set of centers, aiming to improve computational efficiency when dealing with massive data. Trajectory clustering based on probabilistic models attempts to find the best data model to fit the given data, and assumes a model for each cluster, looking for the best fit of the data to the given model. Gaussian mixture models are often used to fit the data in probabilistic model-based trajectory clustering [
18,
19]. Zeng et al. [
18] considered that the Gaussian mixture model could give the class probability to which each trajectory belongs, so they used the Gaussian mixture clustering method to identify and mine the prevailing flight patterns of aircraft in the terminal area.
Since each clustering method has its advantages and limitations, we can ensemble a variety of clustering methods to give full play to their respective advantages, that is, clustering ensemble, which has become a better direction of research in current trajectory clustering [
20,
21,
22,
23,
24]. In addition, since deep learning exhibits great autonomy, it is also a valuable research direction in the future to use deep learning to automatically learn the final clustering results from massive data [
18]. Olive et al. [
25] introduced two deep trajectory clustering methods implemented with autoencoders, which cluster high-dimensional data according to their representation in a low-dimensional space. In addition, Pasi Franti et al. [
26] proposed a prototype swap clustering method, clustering by swapping a series of prototypes (cluster center trajectories) and using K-means to fine-tune the positions of these prototype trajectories. In essence, this method only has one more prototype trajectory swap step than K-means, but it can achieve high-quality clustering through a random search strategy.
At present, most trajectory clustering uses a single clustering algorithm. When other processing remains unchanged, a single clustering method encounters a bottleneck in improving the clustering effect. In addition, when the dimension and length of the data are large, it is difficult for most clustering algorithms to maintain high computational efficiency on massive data sets. In addition, most of the current trajectory clustering is based on the attributes such as longitude, latitude, and altitude of the trajectory. How to make full use of the existing attributes is also a problem that should be paid attention to in the clustering.
In this paper, a clustering ensemble method of aircraft trajectory based on a similarity matrix is proposed. To efficiently utilize the existing attributes, a derived attribute that can describe some inherent law of the data is constructed. To improve computational efficiency, the Stacked autoencoder is used to learn efficient feature representations of the trajectories, which are used as inputs to subsequent clustering algorithms. Multiple different basis clusters are used to generate diverse clustering results, and the clustering ensemble method based on a similarity matrix is used to ensemble each clustering result to obtain more robust results. Summarizing the main contributions of this paper are as follows: (a) The derived attributes that can effectively characterize the trajectory shape information are constructed from the existing features empirically. (b) As far as we know, this paper is the first time to use a clustering ensemble to solve the problem of trajectory clustering, which provides a new way for related researchers to solve the problem of trajectory clustering. The clustering ensemble method based on a similarity matrix is used to ensemble the results of each base cluster, which eliminates the inherent randomness of the single clustering algorithm itself.
The rest of the paper is organized as follows.
Section 2 describes the theory and implementation process of the trajectory clustering ensemble method based on the similarity matrix proposed in this paper.
Section 2.1 introduces the derived property of the angle of construction,
Section 2.2 introduces the process of learning trajectory features from the original data using the stacked autoencoder, and
Section 2.3 describes the clustering ensemble method based on the similarity matrix, which is the focus of this section and the whole article.
Section 3 presents the experimental results and discusses the superiority and effectiveness of our method. Finally,
Section 4 summarizes the work carried out in this paper and looks forward to future research directions.
2. Methodology
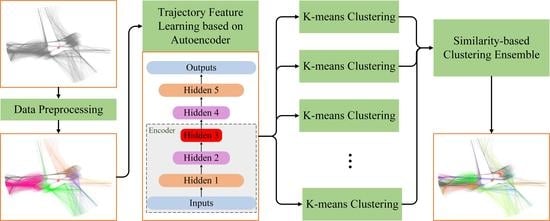
To solve the bottleneck problem faced by a single clustering algorithm in improving the clustering accuracy of aircraft trajectories, a clustering ensemble method of aircraft trajectory based on a similarity matrix is proposed in this paper. The implementation process of this method is shown in
Figure 1. (1) Preprocess the data, including data cleaning, unifying trajectory lengths, transforming coordinates, feature normalization, separation of arrivals and departures, and dividing the dataset by runways and corridors. (2) Construct the derived property of angle empirically. (3) Use the stacked autoencoder to learn features that can efficiently represent trajectories. (4) Use the processed data obtained above as the input of each K-means basis cluster to acquire multiple clustering results. (5) Adopt the similarity-based clustering ensemble method to obtain the corresponding similarity matrix according to the results of each basis cluster [
23]. Use all similarity matrixes to obtain the consistent similarity matrix. Next, (6) Take the deformation of the consistent matrix as the distance matrix between trajectories, and use agglomerative hierarchical clustering to ensemble the results of each basis cluster on the distance matrix, obtaining the final ensembled clustering results.
2.1. Data Preprocessing
Firstly, the quality analysis and cleaning of the trajectory data are carried out. Explore data for missing, duplicate, and mistyped waypoint data with quality analysis. If there is the duplicate and wrong type of waypoint data, delete it directly. Often, data will be partially missing. The reason for this situation is mostly due to the occasional abnormality of the equipment, which leads to the fact that the trajectory point data is not recorded for a certain period of time. Count the time interval between all adjacent trajectory points for each trajectory. According to the specific conditions of the data, for a certain trajectory, if the time interval between two consecutive points exceeds a certain threshold, the trajectory will be deleted. Second, unify the trajectory length. Count the number of trajectory points (trajectory length) for each trajectory. For the trajectory that is too short, delete it directly. Since the trajectory with too short a length cannot reflect the entire landing or take-off process of the aircraft in the terminal area, it is not beneficial to the subsequent clustering. On this basis, in order to use Euclidean distance to measure the similarity between trajectories, all trajectories are sampled to the same length by sampling. This is because Euclidean distance requires component correspondence. Of course, researchers can also choose the here methods to measure the similarity between trajectories without forcing the trajectories to have the same length [
27,
28].
In order to more intuitively reflect the trajectory position centered on the airport, the latitude and longitude coordinates in the data are converted into ENU (East-North-Up) Cartesian coordinate system with the center of the airport as the origin. Then, the values of all features are mapped to between 0 and 1 using the maximum and minimum normalization method, so as to prevent the problem that the value of a feature is generally large/small and the influence of the feature is too large/small. Due to the completely different operating modes of the incoming and outgoing flights, take-off and landing separation are performed on the trajectory. On this basis, in order to prevent the problem of uncontrollable results in the clustering process, the data set is divided into runways and corridors. When dividing the dataset by runway, trajectory points that fall on the runway are not considered. For the landing trajectory, calculate the distance between its last track point and each runway endpoint, and the runway represented by the nearest runway endpoint is the runway to which the track belongs. For a takeoff track, calculate the distance from its first track point to each runway endpoint. Next, divide the data set according to the corridors. For the landing trajectory, calculate the distance between its first trajectory point and each corridor, and the nearest corridor is the corridor to which it belongs. For the takeoff trajectory, calculate the distance between its last trajectory point and each corridor entrance.
It should be noted that the above data preprocessing steps do not take a long time. Since it mainly includes a simple data cleaning and data set division. Data set division also only needs to calculate the Euclidean distance between points, and the computational complexity is relatively low.
2.2. Derived Attribute Construction
Since the shape feature of the trajectory cannot be reflected by its three-dimensional spatial position and heading features, to express the shape information of the trajectory, we construct an angle feature, denoted as
. For a trajectory containing
points, the angle value
of each trajectory point
is represented by the counterclockwise angle between the two line segments formed by points
,
and
, where
and
are the two points immediately before and after the point
. (Except for its first point
and last point
.). The calculation method of
is shown in formula (1). Each symbol in the formula (1) can be represented in
Figure 2.
In formula (1), represents the length of the horizontal line connecting the trajectory point and the immediately preceding trajectory point , represents the length of the horizontal line connecting the trajectory point and the immediately following trajectory point , represents the length of the horizontal line connecting the two trajectory points and before and after the trajectory point.
It should be noted that there is no point before the first point of the trajectory and there is no point after the last point . So for the angle values of and , the angle values of the next point of and the previous point of are used as the angle values of and , respectively.
2.3. Trajectory Feature Learning Based on the Stacked Autoencoder
Clustering analysis needs to use a large amount of historical trajectory data to make the results more regular and convincing, which leads to a larger length of data. In addition, the essence of the trajectory is a time series. If the entire trajectory is used as the clustering object, it is generally necessary to expand it into a row vector according to the time sequence during processing. Assuming that a trajectory has 90 points, and each trajectory point has only three spatial position features, then its dimensions also have as many as 270 dimensions. If a trajectory has more features and points, it will also have a larger dimension. This will seriously affect computational efficiency. At the same time, if there are too many trajectory points, redundant information may exist, or there may be a certain pattern, so it is unnecessary to use too many dimensions to represent a trajectory. Therefore, to improve the computational efficiency, we perform feature extraction and dimensionality reduction on the trajectory data.
An autoencoder is an artificial neural network that learns to efficiently represent input data through unsupervised learning. Its goal is to restore the original input data with as little loss as possible. This coincides with our needs. A simple autoencoder refers to a neural network with only one input layer, one hidden layer, and one output layer [
29]. However, the neural network has the same number of neurons in the input and output layers to try to reconstruct the input. The autoencoder network does not need data labels but uses the difference between the input and output to guide the network for training to find the optimal network parameters, so its objective function is shown in Equation (1). Therefore, it is a kind of unsupervised learning [
30]. All types of autoencoders usually contain two parts, one is the encoder, which is the layer-by-layer learning from the input layer to the hidden layer, which learns to turn the input into an internal representation. The other is the decoder, which is layer-by-layer learning from the hidden layer to the output layer, which learns to reconstruct the input using the internal representation.
Since a simple autoencoder contains only one hidden layer, it may not be sufficient in some complex cases. Therefore, multi-layer autoencoders with multiple hidden layers called stacked autoencoders appeared. It can learn more complex encoded representations. In this paper, the stacked autoencoder is used for trajectory feature learning, and each trajectory is processed into a row vector in time sequence and input into the stacked autoencoder network. The stacked autoencoder takes the output of the hidden layer of its previous autoencoder as the input of its subsequent autoencoder, and the process can be represented in
Figure 3. After integrating the individual autoencoders, the network structure of the stacked autoencoder is symmetric about the middle hidden layer. The network structure of a stacked autoencoder with
hidden layers is shown in
Figure 4. In practical applications, the output of the hidden layer of the last autoencoder is usually used, that is, the output of the middle hidden layer of the entire stacked autoencoder network.
The practice has shown that too many hidden layers can also cause the stacked autoencoder to fail to learn useful features. In application, the network hyperparameters including the number of hidden layers are generally set according to the training data and training effects and through a large number of experiments. According to the dimension and length of the specific data, set each parameter to be a set within a certain value range, and then randomly select N from all possible network hyperparameter combinations. Then, the parameter configuration that minimizes the objective function value is the optimal parameter, which is the network hyperparameter we are looking for.
2.4. Trajectory Clustering Ensemble Based on the Similarity Matrix
At present, most trajectory clustering uses a single clustering method for clustering. When other processing remains unchanged, it is difficult to improve the clustering effect by using a single clustering method. If we want to improve the clustering effect on this basis, we can use multiple different clustering methods to generate multiple clustering results, and then combine these clustering results to make full use of the information contained in each result to obtain cluster ensemble results of higher quality [
21]. This approach is called cluster ensemble. The key and difficult problem of clustering ensemble is how to properly express and combine the results of each basis cluster. Clustering ensembles can be roughly classified into similarity-based methods, graph-based methods, relabeling-based methods, and transformation-based methods [
21,
22,
31]. Among them, the basic idea of the similarity-based method is to use the clustering results of multiple basis clusters to obtain a consistent similarity matrix and use the consistent similarity matrix to express the connection and information between each basis cluster. The method is easy to implement and aggregate, and can be used to ensemble multiple clustering methods.
Therefore, this paper adopts the clustering ensemble method based on similarity to ensemble the clustering results of multiple K-means basis clusters. When integrating the individual clustering results, the data clustering method based on evidence accumulation was proposed by Fred et al. [
23] was introduced. According to the results of each basis cluster, the corresponding similarity matrix is obtained, and these similarity matrices are used to generate a consistent similarity matrix, and then the deformation of the consistent similarity matrix is used as the distance matrix between trajectories. Under a certain aggregation threshold level, using agglomerative hierarchical clustering to obtain ensemble clustering results. This process can be represented in
Figure 5. The idea of agglomerative hierarchical clustering is to first treat each sample as a cluster, and then repeatedly merge the two closest clusters until the iteration termination condition is satisfied or all samples are in one cluster [
32]. There are single connections, full connections, and average connections for calculating the distance between clusters [
33].
The specific implementation steps of the trajectory clustering ensemble method based on similarity in this paper are as follows:
Assuming that the input dataset has trajectories, each trajectory is denoted as . Then the dataset is denoted as .
Step 1: Run the K-means algorithm times on the data set , and each time you can select the same or the different number of parameter clusters , thereby obtaining clustering results . where is a -dimensional vector , and each element of represents the clustering label for each trajectory.
Step 2: Obtain the corresponding similarity matrix from each clustering result . A consistent similarity matrix is obtained from these similarity matrices. The rules for generating the similarity matrix according to the result of the basis cluster are as follows: if , it means that the clustering categories of the trajectories and are the same, that is, they are in the same cluster, then the element of the similarity matrix , otherwise . So each similarity matrix is a binary matrix whose each element indicates whether each pair of trajectories occurs in the same cluster. The consistent similarity matrix is equal to the average of these similarity matrices, that is, , where the value of every element of is between 0 and 1, indicating that trajectories and have probability of appearing in the same cluster in the results of the basis clusters. The idea of generating each element in the consensus similarity matrix here is similar to the principle of majority voting.
Step 3: Take
as the distance between trajectories
and
, that is, take
as the distance matrix, and use the single-connected agglomerative hierarchical clustering algorithm (
) as the consistent cluster to find consistent clusters at the threshold level
[
23]. Since the value of each element of the matrix
is between 0 and 1, every element of the matrix
also has a value between 0 and 1. The specific meaning of the threshold
is: when the distance between the two closest clusters is less than
, the two clusters are merged, otherwise they are not merged. The value range of
is between 0 and 1, and its empirical value is 0.5.
To sum up, there are three parameters that need to be adjusted in the trajectory clustering ensemble method based on similarity in this paper, one is the number of basis clusters, one is the number of clusters of each basis cluster, and one is the connection threshold
. The pseudocode of this method is shown in Algorithm 1. If you want to use other basis clusters, the basis clusters
can also be replaced by other clustering methods. The method of adjusting the parameters adopts the method mentioned at the end of
Section 2.1, that is, given the optional value of each parameter, and then randomly selects N from all parameter combinations for the experiment, and this N is also the number of experiments. The parameter combination that minimizes the sum of squared errors within the cluster SSE (see
Section 3.2 for the clustering evaluation index SSE) is the optimal parameter configuration.
| Algorithm 1. Clustering ensemble algorithm based on similarity |
Inputs: (1) Data Set ;
(2) The number of basis clusters, ;
(3) Number of clusters per basis cluster, ;
(4) Basis Cluster, ;
(5) Consistent Cluster, ;
(6) The threshold level, ;
Outputs: Cluster ensemble results, ;
Algorithm: - 1.
for: - 2.
; - 3.
Generate a basis similarity matrix of based on ; - 4.
end for - 5.
Generate a consistent similarity matrix ; - 6.
Take as the distance matrix between all trajectories, where is the distance between trajectories and ; - 7.
Use a single-linked agglomerative hierarchical clustering algorithm at a threshold level to find consistent clustering results ;
|
4. Conclusions
Massive trajectory data contains inherent information such as the prevailing flight patterns of aircraft. At present, the most efficient way to mine this information is to perform cluster analysis on trajectories. However, since most of the trajectory clustering algorithms used in the current are the single clustering algorithm, it is difficult to improve the clustering effect by this method. Therefore, this paper introduces a trajectory clustering ensemble method based on a similarity matrix. Firstly, in the data preprocessing stage, the trajectory dataset is divided according to the runway and corridor to which each trajectory belongs. To make full use of the information in the trajectory data, an angular feature that can express the shape of the trajectory is also constructed. Secondly, to reduce the data dimension, the stacked autoencoding network is used to perform feature learning on each dataset, and data that can represent the original trajectory with fewer features is obtained. Next, each dataset is clustered using multiple K-means basis clusters. Finally, the clustering ensemble method based on a similarity matrix is adopted to ensemble the results of each basis cluster. Through the experimental verification, it is found that compared with the single clustering algorithm, higher quality and more robust clustering results can be obtained by using the trajectory clustering ensemble method based on the similarity matrix proposed in this paper. The method does not depend on a specific dataset and can handle a wider variety of dataset types, so it can be used in other terminal areas and generalized to enroute flight scenarios. In the future, we can continue to study the ensemble of different clustering methods to explore more efficient ensemble methods.