1. Introduction
Our society is immersed in a flow of data that supports all kinds of services and facilities such as online TV and radio, social networks, medical and remote sensing applications, or information systems, among others. The data employed in these applications are different, from text and audio to images and videos, strands of DNA, or environmental indicators, with a long etcetera. In many scenarios, these data are transmitted and/or stored for a fixed period of time or indefinitely. Despite enhancements on networks and storage devices, the amount of information globally generated increases so rapidly that only a small part can be saved [
1,
2].
Data compression is the solution to relieve Internet traffic congestion and the storage necessities of data centers.
The compression of information has been a field of study for more than a half-century. Since C. Shannon established the bases of information theory [
3], the problem of how to reduce the number of bits to store an original message has been a relevant topic of study [
4,
5,
6]. Depending on the data type and their purposes, the compression regime may be lossy or lossless. Image, video, and audio, for example, often use lossy regimes because the introduction of some distortion in the coding process does not disturb a human observer and achieves higher compression ratios [
6]. Lossless regimes, on the other hand, recover the original message losslessly but achieve lower compression ratios. Also depending on the type and purpose of the data, the compression system may use different techniques. There are many systems specifically devised for particular types of data. Image and video compression capture samples that are transformed several times to reduce their visual redundancy [
7,
8,
9,
10]. Contrarily, compression of DNA often relies on a reference sequence to predict only the dissimilarities between the reference and the source [
11]. There are universal methods like Lempel–Ziv–Welch [
12,
13] that code any kind of data, although they do not achieve the high compression ratios that specifically devised systems yield. In recent years, deep-learning techniques have been spread in many compression schemes to enhance transformation and prediction techniques, obtaining competitive results in many fields [
14,
15,
16,
17].
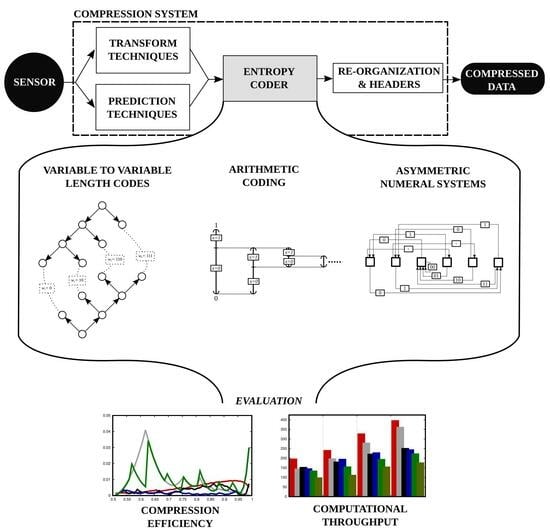
Regardless of the coding system and the regime employed, most compression schemes rely on a coding stage called
entropy coding to reduce the amount of information needed to represent the original data. See in
Figure 1 that this stage is commonly situated just after the transformation and/or prediction stages. These stages prepare the data for the entropy coder producing binary symbols
x with a corresponding probability
. In general, these symbols are (transformed to) binary, so
is assumed in the following. The estimated or real [
18,
19] probability
depends on the amount of redundancy found in the original data. Adjacent pixels in an image often have similar colors, for instance, so their binary representation can be predicted with a high probability. Both
x and
are fed to the entropy coder, which produces a compact representation of these symbols attaining compression. As Shannon’s theory of entropy dictates, the higher the probability of a symbol the lower its entropy, so higher compression ratios can be obtained. The main purpose of entropy coders is to attain coding efficiency close to the entropy of the original message while spending low computational resources, so large sets of data can be processed rapidly and efficiently.
Arguably, there are three main families of entropy coders. The first employs techniques that map one (or some) source symbols to codewords of different lengths. Such techniques exploit the repetitiveness of some symbols to represent them with a short codeword. The most complete theoretical model of such techniques is
variable-to-variable length codes (V2VLC) [
20,
21]. The first entropy-coding technique proposed in the literature, namely Huffman coding [
22], uses a similar technique that maps each symbol to a codeword of variable length. Other techniques similar to V2VLC are Golomb-Rice coding [
23,
24], Tunstall codes [
25,
26], or Khodak codes [
27], among others [
20,
28], which have been adopted in many scenarios [
29,
30,
31,
32]. The second main family of entropy coders utilizes a technique called
arithmetic coding (AC) [
33]. The main idea is to divide a numeric interval into subintervals of varying sizes depending on the probability of the source symbols. The coding of any number within the latest interval commonly requires fewer bits than the original message and allows the decoder to reverse the procedure. Arithmetic coding has been widely spread and employed in many fields and standards [
34,
35,
36,
37] and there exist many variations and architectures [
38,
39,
40,
41,
42,
43]. The latest family of entropy coders is based on
asymmetric numeral systems (ANS), which is a technique introduced in the last decade [
44]. ANS divides the set of natural numbers into groups that have a size depending on the probability of the symbols. The coding of the original message then traverses these groups so that symbols with higher probabilities employ the groups of the largest size. The decoder reverses the path from the last to the first group, recovering the original symbols. There are different variants of ANS such as the range ANS or the uniform binary ANS, though the tabled ANS (tANS) is the most popular [
45,
46,
47] since it can operate like a finite-state machine achieving high throughput. tANS has been recently adopted in many compression schemes [
11,
48,
49], so it is employed in this work to represent this family of entropy coders.
The popularity of the aforementioned entropy-coding techniques has changed depending on the trends and necessities of applications. Since entropy coding is at the core of the compression scheme, efficiency, and speed are two important features. Before the introduction of ANS, Huffman coding and variants of V2VLC were generally considered the fastest techniques because they use direct mapping between source symbols and codewords. Nonetheless, they are not the most efficient in terms of compression [
50]. Arithmetic coding was preferable in many fields due to its highest compression efficiency although it was criticized since it commonly requires some arithmetic operations to code each symbol, achieving lower computational throughput [
51]. Recent works claim that tANS achieves the efficiency of arithmetic coding while spending the computational costs of Huffman coding [
44,
52]. Although these discussions and claims are well grounded, they are commonly framed for a specific scheme or scenario without considering and evaluating other techniques. Unlike the previously cited references, this work provides a common framework to appraise different entropy coders. It also provides simple software architectures to test and optimize them using different coding conditions. The experimental evaluation discerns the advantages and shortcomings of each family of coders. The result of this evaluation is the main contribution of this work, which may help to select this coding stage in forthcoming compression schemes.
The rest of the paper is organized as follows.
Section 2 describes the entropy coders evaluated in this work and proposes a software architecture for each. This section is divided into three subsections, one for each family of entropy coders.
Section 2.1 presents a general method for V2VLC that uses pre-computed codes. Arithmetic coding is tackled in
Section 2.2 describing two coders widely employed in image and video compression and an arithmetic coder that uses codewords of fixed length.
Section 2.3 describes the tANS coding scheme and proposes two architectures for its implementation. All these coders are evaluated in terms of compression efficiency and computational throughput in
Section 3, presenting experimental results obtained with different coding conditions. The last section discusses the results and provides conclusions.