Efficient Ontology Meta-Matching Based on Interpolation Model Assisted Evolutionary Algorithm
Abstract
:1. Introduction
- a mathematical optimization model on EA-IM based ontology meta-matching problem is constructed;
- a binomial IM based on lattice design is presented to forecast the fitness of the individuals, which is constructed according to the relationship between ontology alignment’s two evaluation metrics;
- an EA-IM is proposed to efficiently address the ontology meta-matching problem.
2. Related Work
3. Preliminaries
3.1. Ontology, Ontology Alignment and Ontology Matching Process
- C is a nonempty set of classes;
- P is a nonempty set of properties;
- I is a nonempty set of instances:
- : associates a property with two classes;
- : associates a class with a subset of I which represents the instances of the concept c;
- : associates a property with a subset of Cartesian product which represents the pair of instances related through the property p.
- is the identifier of the matching element;
- and are entities of ontology and , respectively;
- is the confidence value of the matched element (generally in the range [0, 1]);
- represents the matching relation between entities and , such as equivalence relation or generalization relation.
3.2. Similarity Measure
3.3. Similarity Aggregation Strategy
3.4. Ontology Meta-Matching Problem
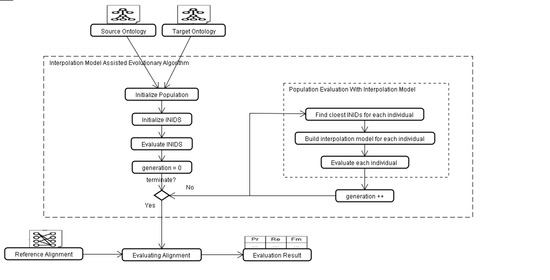
4. Evolutionary Algorithm with Interpolation Model
4.1. Encoding Mechanism
4.2. Binomial Interpolation Model Based on Lattice Design
4.3. Selection, Crossover and Mutation
5. Experiment
5.1. Experimental Configuration
- Population size = 20,
- Crossover probability = 0.6,
- Mutation probability = 0.01,
- Maximum generation = 1000,
- Population size. The setting of the population size depends on the complexity of the individual, and according to previous studies [39], population size should be in the range [4, 6] where n is the decision variable’s dimension number. In this work, the decision variable owns 4 dimensions, so the population size should be in the range [16, 24]. The larger population size is, the longer time population might take to converge. While the smaller it is, the higher probability of which the algorithm suffers from the premature convergence [40]. Since the ontology meta-matching is a small-scale issue, we set the population size as 20.
- Crossover and mutation probability. For crossover and mutation probabilities, small probabilities will decrease the diversity of the population while large probabilities will miss the optimal individuals [41]. Their suggested ranges are, respectively, [0.6, 0.8] and [0.01, 0.05], and since the problem in this work is a low-dimensional problem, we select and , whose effectiveness are also verified in the experiment.
- Maximum generation. In EA, the maximum of generations is directly proportional to the scale of the problem [42], and the suggested range is [800, 2000]. Since the ontology meta-matching problem in this work is a 4-dimensional problem, who’s searching region is not very large, the maximum generation should be a relative small value, and in the experiment, is robust on all testing cases.
5.2. Experimental Results
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guarino, N.; Oberle, D.; Staab, S. What is an ontology? In Handbook on Ontologies; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–17. [Google Scholar]
- Arens, Y.; Chee, C.Y.; Knoblock, C.A. Retrieving and Integrating Data from Multiple Information Sources. Int. J. Coop. Inf. Syst. 1993, 2, 127–158. [Google Scholar] [CrossRef]
- Baumbach, J.; Brinkrolf, K.; Czaja, L.F.; Rahmann, S.; Tauch, A. CoryneRegNet: An ontology-based data warehouse of corynebacterial transcription factors and regulatory networks. BMC Genom. 2006, 7, 24. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Ni, Z.; Cao, H. Research on association rules mining based-on ontology in e-commerce. In Proceedings of the 2007 International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 21–25 September 2007; pp. 3549–3552. [Google Scholar]
- Tu, S.W.; Eriksson, H.; Gennari, J.H.; Shahar, Y.; Musen, M.A. Ontology-based configuration of problem-solving methods and generation of knowledge-acquisition tools: Application of PROTÉGÉ-II to protocol-based decision support. Artif. Intell. Med. 1995, 7, 257–289. [Google Scholar] [CrossRef]
- Gruber, T.R. A translation approach to portable ontology specifications. Knowl. Acquis. 1993, 5, 199–220. [Google Scholar] [CrossRef]
- Kashyap, V.; Sheth, A. Semantic heterogeneity in global information systems: The role of metadata, context and ontologies. Coop. Inf. Syst. Curr. Trends Dir. 1998, 139, 178. [Google Scholar]
- Doan, A.; Madhavan, J.; Domingos, P.; Halevy, A. Ontology matching: A machine learning approach. In Handbook on Ontologies; Springer: Berlin/Heidelberg, Germany, 2004; pp. 385–403. [Google Scholar]
- Verhoosel, J.P.; Van Bekkum, M.; van Evert, F.K. Ontology matching for big data applications in the smart dairy farming domain. In Proceedings of the OM, Bethlehem, PA, USA, 11–12 October 2015; pp. 55–59. [Google Scholar]
- Martinez-Gil, J.; Aldana-Montes, J.F. An overview of current ontology meta-matching solutions. Knowl. Eng. Rev. 2012, 27, 393–412. [Google Scholar] [CrossRef]
- Xue, X.; Huang, Q. Generative adversarial learning for optimizing ontology alignment. Expert Syst. 2022, e12936. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Cully, A.; Togelius, J. AlphaStar: An Evolutionary Computation Perspective. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, GECCO ’19, Prague, Czech Republic, 13–17 July 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 314–315. [Google Scholar] [CrossRef]
- Vikhar, P.A. Evolutionary algorithms: A critical review and its future prospects. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016; pp. 261–265. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. What is an evolutionary algorithm? In Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2015; pp. 25–48. [Google Scholar]
- Jiao, Y.; Xu, G. Optimizing the lattice design of a diffraction-limited storage ring with a rational combination of particle swarm and genetic algorithms. Chin. Phys. C 2017, 41, 027001. [Google Scholar] [CrossRef]
- Naya, J.M.V.; Romero, M.M.; Loureiro, J.P.; Munteanu, C.R.; Sierra, A.P. Improving ontology alignment through genetic algorithms. In Soft Computing Methods for Practical Environment Solutions: Techniques and Studies; IGI Global: New York, NY, USA, 2010; pp. 240–259. [Google Scholar]
- Martinez-Gil, J.; Aldana-Montes, J.F. Evaluation of two heuristic approaches to solve the ontology meta-matching problem. Knowl. Inf. Syst. 2011, 26, 225–247. [Google Scholar] [CrossRef] [Green Version]
- He, H.; Tan, Y. A two-stage genetic algorithm for automatic clustering. Neurocomputing 2012, 81, 49–59. [Google Scholar] [CrossRef]
- Huang, H.D.; Acampora, G.; Loia, V.; Lee, C.S.; Kao, H.Y. Applying FML and fuzzy ontologies to malware behavioural analysis. In Proceedings of the 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011), Taipei, Taiwan, 27–30 June 2011; pp. 2018–2025. [Google Scholar]
- Xue, X.; Wang, Y.; Ren, A. Optimizing ontology alignment through memetic algorithm based on partial reference alignment. Expert Syst. Appl. 2014, 41, 3213–3222. [Google Scholar] [CrossRef]
- Xue, X.; Liu, J.; Tsai, P.W.; Zhan, X.; Ren, A. Optimizing Ontology Alignment by Using Compact Genetic Algorithm. In Proceedings of the 2015 11th International Conference on Computational Intelligence and Security (CIS), Shenzhen, China, 19–20 December 2015; pp. 231–234. [Google Scholar] [CrossRef]
- Xue, X.; Jiang, C. Matching sensor ontologies with multi-context similarity measure and parallel compact differential evolution algorithm. IEEE Sens. J. 2021, 21, 24570–24578. [Google Scholar] [CrossRef]
- Lv, Z.; Peng, R. A novel meta-matching approach for ontology alignment using grasshopper optimization. Knowl.-Based Syst. 2020, 201–202, 106050. [Google Scholar] [CrossRef]
- Lv, Q.; Zhou, X.; Li, H. Optimizing Ontology Alignments Through Evolutionary Algorithm with Adaptive Selection Strategy. In Advances in Intelligent Systems and Computing, Proceedings of the International Conference on Advanced Machine Learning Technologies and Applications, Cairo, Egypt, 20–22 March 2021; Springer: Cham, Switzerland, 2021; pp. 947–954. [Google Scholar]
- Xue, X.; Yao, X. Interactive ontology matching based on partial reference alignment. Appl. Soft Comput. 2018, 72, 355–370. [Google Scholar] [CrossRef]
- Xue, X. Complex ontology alignment for autonomous systems via the Compact Co-Evolutionary Brain Storm Optimization algorithm. ISA Trans. 2022; in press. [Google Scholar] [CrossRef]
- Xue, X.; Pan, J.S. A segment-based approach for large-scale ontology matching. Knowl. Inf. Syst. 2017, 52, 467–484. [Google Scholar] [CrossRef]
- Winkler, W.E. The State of Record Linkage and Current Research Problems; Statistical Research Division, US Census Bureau: Suitland-Silver Hill, MD, USA, 1999.
- Mascardi, V.; Locoro, A.; Rosso, P. Automatic ontology matching via upper ontologies: A systematic evaluation. IEEE Trans. Knowl. Data Eng. 2009, 22, 609–623. [Google Scholar] [CrossRef]
- Wu, Z.; Palmer, M. Verbs semantics and lexical selection. In Proceedings of the 32nd annual meeting on Association for Computational Linguistics (COLING-94), Las Cruces, NM, USA, 27–30 June 1994. [Google Scholar]
- Ferranti, N.; Rosário Furtado Soares, S.S.; de Souza, J.F. Metaheuristics-based ontology meta-matching approaches. Expert Syst. Appl. 2021, 173, 114578. [Google Scholar] [CrossRef]
- Fellbaum, C. WordNet. In Theory and Applications of Ontology: Computer Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 231–243. [Google Scholar]
- Golberg, D.E. Genetic algorithms in search, optimization, and machine learning. Addion Wesley 1989, 1989, 36. [Google Scholar]
- Ehrig, M.; Euzenat, J. Relaxed precision and recall for ontology matching. In Proceedings of the K-Cap 2005 Workshop on Integrating Ontology, Banff, AB, Canada, 2 October 2005; pp. 25–32. [Google Scholar]
- Faria, D.; Pesquita, C.; Santos, E.; Palmonari, M.; Cruz, I.F.; Couto, F.M. The agreementmakerlight ontology matching system. In Lecture Notes in Computer Science, Proceedings of the OTM Confederated International Conferences “On the Move to Meaningful Internet Systems”, Graz, Austria, 9–13 September 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 527–541. [Google Scholar]
- Acampora, G.; Loia, V.; Vitiello, A. Enhancing ontology alignment through a memetic aggregation of similarity measures. Inf. Sci. 2013, 250, 1–20. [Google Scholar] [CrossRef]
- Yates, F. A new method of arranging variety trials involving a large number of varieties. J. Agric. Sci. 1936, 26, 424–455. [Google Scholar] [CrossRef]
- Achichi, M.; Cheatham, M.; Dragisic, Z.; Euzenat, J.; Faria, D.; Ferrara, A.; Flouris, G.; Fundulaki, I.; Harrow, I.; Ivanova, V.; et al. Results of the ontology alignment evaluation initiative 2016. In Proceedings of the OM: Ontology Matching, Kobe, Japan, 18 October 2016; pp. 73–129. [Google Scholar]
- Liu, X. A research on Population Size Impaction on the Performance of Genetic Algorithm. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2010. [Google Scholar]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks; Springer: Berlin/Heidelberg, Germany, 2019; pp. 43–55. [Google Scholar]
- Xue, X.; Wang, Y. Using memetic algorithm for instance coreference resolution. IEEE Trans. Knowl. Data Eng. 2015, 28, 580–591. [Google Scholar] [CrossRef]
- Xue, X.; Chen, J. Matching biomedical ontologies through Compact Differential Evolution algorithm with compact adaption schemes on control parameters. Neurocomputing 2021, 458, 526–534. [Google Scholar] [CrossRef]











| (0.3, 0.3, 0.3, 0.3) | (0.3, 0.3, 0.3, 0.6) |
| (0.3, 0.3, 0.6, 0.3) | (0.3, 0.3, 0.6, 0.6) |
| (0.3, 0.6, 0.3, 0.3) | (0.3, 0.6, 0.3, 0.6) |
| (0.3, 0.6, 0.6, 0.3) | (0.3, 0.6, 0.6, 0.6) |
| (0.6, 0.3, 0.3, 0.3) | (0.6, 0.3, 0.3, 0.6) |
| (0.6, 0.3, 0.6, 0.3) | (0.6, 0.3, 0.6, 0.6) |
| (0.6, 0.6, 0.3, 0.3) | (0.6, 0.6, 0.3, 0.6) |
| (0.6, 0.6, 0.6, 0.3) | (0.6, 0.6, 0.6, 0.6) |
| Testing Case | EA-IM | EA-IM | EA-IM | EA | EA | EA |
|---|---|---|---|---|---|---|
| 101 | 1.000 (0.000) | 1.000 (0.024) | 1.000 (0.013) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 103 | 1.000 (0.003) | 1.000 (0.009) | 1.000 (0.006) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 104 | 1.000 (0.000) | 1.000 (0.003) | 1.000 (0.002) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 201 | 0.989 (0.005) | 0.907 (0.007) | 0.946 (0.005) | 0.989 (0.000) | 0.928 (0.000) | 0.957 (0.000) |
| 203 | 1.000 (0.000) | 0.979 (0.424) | 0.990 (0.390) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 204 | 1.000 (0.000) | 0.990 (0.041) | 0.995 (0.023) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 205 | 0.974 (0.009) | 0.794 (0.014) | 0.875 (0.012) | 0.989 (0.000) | 0.918 (0.004) | 0.952 (0.002) |
| 206 | 1.000 (0.006) | 0.876 (0.065) | 0.934 (0.041) | 1.000 (0.000) | 0.928 (0.000) | 0.963 (0.000) |
| 207 | 1.000 (0.009) | 0.887 (0.037) | 0.940 (0.024) | 1.000 (0.000) | 0.938 (0.000) | 0.968 (0.000) |
| 221 | 1.000 (0.000) | 0.990 (0.005) | 0.995 (0.002) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 222 | 1.000 (0.007) | 1.000 (0.008) | 1.000 (0.007) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 223 | 0.990 (0.005) | 0.990 (0.005) | 0.990 (0.005) | 1.000 (0.000) | 0.990 (0.000) | 0.995 (0.000) |
| 224 | 1.000 (0.000) | 1.000 (0.024) | 1.000 (0.013) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 225 | 1.000 (0.000) | 1.000 (0.005) | 1.000 (0.003) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 228 | 1.000 (0.014) | 1.000 (0.012) | 1.000 (0.011) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 230 | 0.935 (0.000) | 1.000 (0.000) | 0.966 (0.000) | 0.986 (0.001) | 0.986 (0.000) | 0.986 (0.001) |
| 231 | 1.000 (0.000) | 1.000 (0.005) | 1.000 (0.002) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 232 | 1.000 (0.000) | 1.000 (0.005) | 1.000 (0.003) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 233 | 1.000 (0.015) | 1.000 (0.015) | 1.000 (0.013) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 236 | 1.000 (0.015) | 1.000 (0.015) | 1.000 (0.015) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 237 | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.001) | 1.000 (0.000) | 1.000 (0.001) |
| 238 | 0.990 (0.005) | 0.979 (0.005) | 0.984 (0.005) | 0.990 (0.000) | 0.990 (0.000) | 0.990 (0.000) |
| 239 | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 240 | 0.969 (0.000) | 0.939 (0.000) | 0.954 (0.000) | 1.000 (0.009) | 0.970 (0.000) | 0.985 (0.005) |
| 241 | 1.000 (0.014) | 1.000 (0.014) | 1.000 (0.012) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 246 | 1.000 (0.000) | 0.966 (0.000) | 0.983 (0.000) | 1.000 (0.000) | 1.000 (0.000) | 1.000 (0.000) |
| 247 | 0.969 (0.000) | 0.939 (0.000) | 0.954 (0.000) | 1.000 (0.009) | 0.970 (0.000) | 0.985 (0.005) |
| 248 | 1.000 (0.000) | 0.010 (0.000) | 0.020 (0.000) | 0.500 (0.000) | 0.021 (0.000) | 0.040 (0.000) |
| 301 | 0.960 (0.008) | 0.814 (0.007) | 0.881 (0.006) | 0.980 (0.001) | 0.814 (0.000) | 0.889 (0.001) |
| 302 | 0.906 (0.012) | 0.604 (0.006) | 0.725 (0.005) | 1.000 (0.000) | 0.604 (0.000) | 0.753 (0.000) |
| 303 | 0.884 (0.017) | 0.770 (0.029) | 0.822 (0.023) | 0.870 (0.028) | 0.833 (0.020) | 0.851 (0.001) |
| Average | 0.986 | 0.917 | 0.934 | 0.978 | 0.932 | 0.946 |
| Testing Case | EA-IM | EA |
|---|---|---|
| 101 | 1459 | 32,762 |
| 103 | 1346 | 32,382 |
| 104 | 1448 | 32,214 |
| 201 | 1639 | 32,267 |
| 203 | 1899 | 32,802 |
| 204 | 2116 | 33,212 |
| 205 | 2130 | 33,267 |
| 206 | 1995 | 32,613 |
| 207 | 1784 | 33,615 |
| 221 | 1552 | 32,863 |
| 222 | 1623 | 32,832 |
| 223 | 1663 | 33,643 |
| 224 | 1479 | 33,913 |
| 225 | 2103 | 33,455 |
| 228 | 1721 | 22,436 |
| 230 | 2071 | 28,423 |
| 231 | 1951 | 33,460 |
| 232 | 2066 | 33,181 |
| 233 | 1738 | 22,404 |
| 236 | 1328 | 22,636 |
| 237 | 1735 | 32,362 |
| 238 | 2323 | 34,396 |
| 239 | 1708 | 22,190 |
| 240 | 2005 | 22,326 |
| 241 | 1830 | 22,696 |
| 246 | 1905 | 21,829 |
| 247 | 1818 | 22,177 |
| 248 | 2149 | 32,493 |
| 301 | 2031 | 26,488 |
| 302 | 1869 | 23,982 |
| 303 | 2125 | 25,481 |
| Average | 1826 | 29,395 |
| Testing Case | Edna | AgrMaker | AROMA | ASMOV | CODI | Ef2Match | Falcon | GeRMeSMB | MapPSO | RiMOM | SOBOM | TaxoMap | EA-IM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 101 | 1.00 | 0.99 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.51 | 1.00 |
| 103 | 1.00 | 0.99 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.51 | 1.00 |
| 104 | 1.00 | 0.99 | 0.99 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.51 | 1.00 |
| 201 | 0.04 | 0.92 | 0.95 | 1.00 | 0.13 | 0.77 | 0.97 | 0.94 | 0.42 | 1.00 | 0.95 | 0.51 | 0.95 |
| 203 | 1.00 | 0.98 | 0.80 | 1.00 | 0.86 | 1.00 | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 | 0.49 | 0.99 |
| 204 | 0.93 | 0.97 | 0.97 | 1.00 | 0.74 | 0.99 | 0.96 | 0.98 | 0.98 | 1.00 | 0.99 | 0.51 | 0.99 |
| 205 | 0.34 | 0.92 | 0.95 | 0.99 | 0.28 | 0.84 | 0.97 | 0.99 | 0.73 | 0.99 | 0.96 | 0.51 | 0.88 |
| 206 | 0.54 | 0.93 | 0.95 | 0.99 | 0.39 | 0.87 | 0.94 | 0.92 | 0.85 | 0.99 | 0.96 | 0.51 | 0.93 |
| 207 | 0.54 | 0.93 | 0.95 | 0.99 | 0.42 | 0.87 | 0.96 | 0.96 | 0.81 | 0.99 | 0.96 | 0.51 | 0.94 |
| 221 | 1.00 | 0.97 | 0.99 | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.51 | 0.99 |
| 222 | 0.98 | 0.98 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 0.46 | 1.00 |
| 223 | 1.00 | 0.95 | 0.93 | 1.00 | 1.00 | 1.00 | 1.00 | 0.96 | 0.98 | 0.98 | 0.99 | 0.45 | 0.99 |
| 224 | 1.00 | 0.99 | 0.97 | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 0.51 | 1.00 |
| 225 | 1.00 | 0.99 | 0.99 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.51 | 1.00 |
| 228 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 230 | 0.85 | 0.90 | 0.93 | 0.97 | 0.98 | 0.97 | 0.97 | 0.94 | 0.98 | 0.97 | 0.97 | 0.49 | 0.97 |
| 231 | 1.00 | 0.99 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.51 | 1.00 |
| 232 | 1.00 | 0.97 | 0.97 | 1.00 | 0.97 | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 1.00 | 0.51 | 1.00 |
| 233 | 1.00 | 1.00 | 1.00 | 1.00 | 0.94 | 1.00 | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 236 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 237 | 0.98 | 0.98 | 0.97 | 1.00 | 0.99 | 1.00 | 0.99 | 1.00 | 0.99 | 1.00 | 1.00 | 0.46 | 1.00 |
| 238 | 1.00 | 0.94 | 0.92 | 1.00 | 0.99 | 1.00 | 0.99 | 0.96 | 0.97 | 0.98 | 0.98 | 0.45 | 0.98 |
| 239 | 0.50 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 1.00 | 0.98 | 0.98 | 0.98 | 0.98 | 0.94 | 1.00 |
| 240 | 0.55 | 0.91 | 0.83 | 0.98 | 0.95 | 0.98 | 1.00 | 0.85 | 0.92 | 0.94 | 0.98 | 0.88 | 0.95 |
| 241 | 1.00 | 0.98 | 0.98 | 1.00 | 0.94 | 1.00 | 1.00 | 0.98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| 246 | 0.50 | 0.98 | 0.97 | 0.98 | 0.98 | 0.98 | 1.00 | 0.98 | 0.98 | 0.98 | 0.95 | 0.94 | 0.98 |
| 247 | 0.55 | 0.88 | 0.80 | 0.98 | 0.98 | 0.98 | 1.00 | 0.91 | 0.89 | 0.94 | 0.98 | 0.88 | 0.95 |
| 248 | 0.03 | 0.72 | 0.00 | 0.87 | 0.00 | 0.02 | 0.00 | 0.37 | 0.05 | 0.64 | 0.48 | 0.02 | 0.02 |
| 301 | 0.59 | 0.59 | 0.73 | 0.86 | 0.38 | 0.71 | 0.78 | 0.71 | 0.64 | 0.73 | 0.84 | 0.43 | 0.88 |
| 302 | 0.43 | 0.32 | 0.35 | 0.73 | 0.59 | 0.71 | 0.71 | 0.41 | 0.04 | 0.73 | 0.74 | 0.40 | 0.73 |
| 303 | 0.00 | 0.78 | 0.59 | 0.83 | 0.65 | 0.83 | 0.77 | 0.00 | 0.00 | 0.86 | 0.50 | 0.36 | 0.82 |
| Average | 0.75 | 0.92 | 0.88 | 0.97 | 0.81 | 0.92 | 0.94 | 0.90 | 0.85 | 0.96 | 0.94 | 0.59 | 0.93 |
| Testing Case | Running Time (Second) | F-Measure per Second |
|---|---|---|
| AML | 120 | 0.0031 |
| CroMatcher | 1100 | 0.0008 |
| Lily | 2211 | 0.0004 |
| LogMap | 194 | 0.0028 |
| PhenoMF | 1632 | 0.0000 |
| PhenoMM | 1743 | 0.0000 |
| PhenoMP | 1833 | 0.0000 |
| XMap | 123 | 0.0045 |
| LogMapBio | 54,439 | 0.0000 |
| EA | 29.395 | 0.0322 |
| EA-IM | 1.826 | 0.5115 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, X.; Wu, Q.; Ye, M.; Lv, J. Efficient Ontology Meta-Matching Based on Interpolation Model Assisted Evolutionary Algorithm. Mathematics 2022, 10, 3212. https://doi.org/10.3390/math10173212
Xue X, Wu Q, Ye M, Lv J. Efficient Ontology Meta-Matching Based on Interpolation Model Assisted Evolutionary Algorithm. Mathematics. 2022; 10(17):3212. https://doi.org/10.3390/math10173212
Chicago/Turabian StyleXue, Xingsi, Qi Wu, Miao Ye, and Jianhui Lv. 2022. "Efficient Ontology Meta-Matching Based on Interpolation Model Assisted Evolutionary Algorithm" Mathematics 10, no. 17: 3212. https://doi.org/10.3390/math10173212
APA StyleXue, X., Wu, Q., Ye, M., & Lv, J. (2022). Efficient Ontology Meta-Matching Based on Interpolation Model Assisted Evolutionary Algorithm. Mathematics, 10(17), 3212. https://doi.org/10.3390/math10173212