Price, Complexity, and Mathematical Model

Abstract

The whole world has entered the era of the Vuca. Some traditional methods of problem analysis begin to fail. Complexity science is needed to study and solve problems from the perspective of complex systems. As a complex system full of volatility and uncertainty, price fluctuations have attracted wide attention from researchers. Therefore, through a literature review, this paper analyzes the research on complex theories on price prediction. The following conclusions are drawn: (1) The price forecast receives widespread attention year by year, and the number of published articles also shows a rapid rising trend. (2) The hybrid model can achieve higher prediction accuracy than the single model. (3) The complexity of models is increasing. In the future, the more complex methods will be applied to price forecast, including AI technologies such as LLM. (4) Crude-oil prices and stock prices will continue to be the focus of research, with carbon prices, gold prices, Bitcoin, and others becoming new research hotspots. The innovation of this research mainly includes the following three aspects: (1) The whole analysis of all the articles on price prediction using mathematical models in the past 10 years rather than the analysis of a single field such as oil price or stock price. (2) Classify the research methods of price forecasting in different fields, and found the common problems of price forecasting in different fields (including data processing methods and model selection, etc.), which provide references for different researchers to select price forecasting models. (3) Use VOSviewer to analyze the hot words appearing in recent years according to the timeline, find the research trend, and provide references for researchers to choose the future research direction.

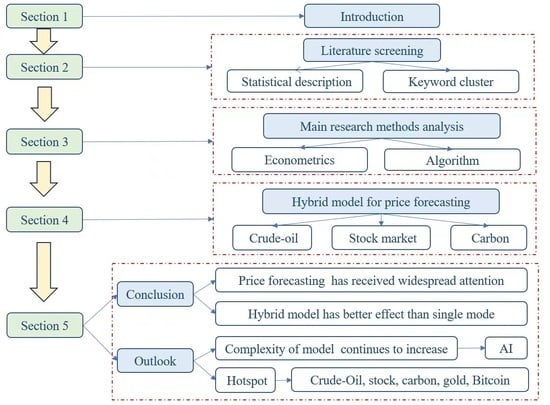
1. Introduction

The world has entered an era of great change. Under the combined effect of the technological revolution, the Internet wave, the economic crisis, regional conflicts, and the social changes brought about by globalization, the world has entered an era of Vuca: full of volatility, uncertainty, complexity, and ambiguity. Before the Vuca era, the world was systematic, precise, and convergent, and many problems could be solved by a fixed theoretical paradigm. However, the problems in the Vuca era have the characteristics of self-growing, constantly jumping, changing, and iterating, which makes the problems intractable and uncontrollable, and traditional methods begin to fail. Complex science has been applied to study and solve problems from the perspective of complex systems.

Complexity science is a new stage in the development of systems science and also one of the frontier fields in the development of contemporary science. Complexity theory is now being applied more and more widely in many fields, such as biology, physics, chemistry, and so on. Hawking S.W., the famous physicist, said that “the 21st century will be the century of complexity science”. Because there are also a large number of nonlinear interactions in economics with dynamic variability and other complex characteristics, complex theory is also widely used in the field of economics (Wu and Ma., 2018 [1]; Ma et al., 2020 [2]; Wu et al., 2023 [3]). Ma and Ren (2016) [4] used a fractional-order IS-LM system to analyze the Hopf bifurcation phenomenon in economic systems and found that the movement of the economic system is characterized by periodicity when the order of the system satisfies certain conditions. Wu and Ma (2023) [5] analyzed the research structure and theoretical evolution of complex economic games through visualization techniques, pointing out that artificial intelligence (AI) is the direction of future research in complex economics.

As one of the important variables in the market economy, price fluctuations are also characterized by complexity. Price not only has the function of conveying market information to people and reflecting changes in supply and demand relations, but also has the function of adjusting economic relations and regulating economic activities (Ma et al., 2022 [6]. Accurate price forecasting can guide enterprises to make correct production and business decisions and reduce the instability of the economic operation process to a certain extent (Ma et al., 2019 [7]). However, due to the influence of various factors, price fluctuations have characteristics such as uncertainty, nonlinearity, and instability, which possess the characteristics of chaotic systems, making accurate price prediction extremely complex (Ma et al., 2021 [8]).

Chaos is the most important discovery in complex systems, and it is the bridge between the two theoretical systems of certainty theory and probability theory. Although there is no consensus on the definition of chaos in the academic community, there is a common understanding of the basic characteristics of chaotic systems. The first characteristic of chaotic systems is ergodicity. Particles moving in chaotic systems will traverse all orbits in a finite time. The second characteristic is internal randomness. Because chaotic systems are sensitive to initial values, small changes in the input will cause huge differences in the output, resulting in the randomness of the output results. The third characteristic is fractal dimension, that is, the random property of chaotic systems is not completely random. Different from completely random systems, chaotic systems have obvious self-similar characteristics and certain internal rules. The last characteristic of chaotic systems is boundedness. The movement of particles in chaotic systems is limited to a certain range. Although the movement seems chaotic and irregular in the short term, it is predictable in the long term. This important conclusion greatly expands the application value of chaotic system analysis and provides support for the long-term prediction of economic systems, financial markets, and weather. The characteristics of price series, such as multiple time scales and nonlinear fluctuations, have the characteristics of chaotic systems.

Many researchers have used complexity theory to predict price fluctuation trends. Many complex mathematical models are used in order to improve prediction accuracy (Ma et al., 2021 [9]). Fan et al. (2015) [10] used the MLE, correlation dimension, and Kolmogorov entropy, the three classical indicators of chaos theory, to identify the chaotic characteristics of the carbon price sequence. And based on phase reconstruction, we established a MPN (multi-layer perceptron neural network) prediction model of carbon prices to characterize its strong nonlinearity. Wang et al. (2018) [11] combined DFN (data fluctuation network) and several AI algorithms, using a complex network time series analysis technique to identify chaotic features of crude oil prices and pre-process the raw data, as shown in Figure 1.

Wu et al. (2021) [12] used bifurcation diagram, Lyapunov exponent, parameter basin, and fractal dimension to analyzed the volatility of electricity price, as showed in Figure 2.

Therefore, this paper will provide an overview of research on this aspect and put forward future research directions to achieve the purpose of more accurate prediction of price fluctuations and reduce the interference on the economy.

The specific structure is arranged as follows: Section 1 is the introduction; Section 2 is the literature screening, statistical description, and keyword analysis; Section 3 is the main research methods analysis; Section 4 is the analysis of hybrid models for price forecasting; and Section 5 is the research conclusion and outlook.

2. Literature Screening, Statistical Description, and Keyword Analysis

2.1. Literature Screening

In order to ensure the quality of this research review, selected two databases, SCIE and SSCI, from the Web of Science Core Collection as the literature source databases. The process of literature review and selection is shown in Figure 3.

Firstly, search for the topics “price fluctuations/price volatility/price forecast/price predict” + All field “mathematical model” (570/2508/1028/4 articles), respectively. After merging and removing duplicate literature, 3590 were left. Removing reviews, left 3553. In order to reflect the latest research trends of the past 10 years, excluding those before 2015, leaving 2349. Last, select 2349 pieces of literature as the basis for analysis. This section first provides a basic statistical description and analysis of the literature.

2.2. Statistical Descriptive Analysis

After preliminary analysis, it was found that these articles have the following four characteristics.

2.2.1. The Number of Publications and Citations Basically Increased Year by Year

By classifying these articles in chronological order, it can be found that the number of publications and citations has been increasing year by year since 2015, as shown in Figure 4.

In 2015, the number of citations was only 79, and in 2016, it reached 288. Although the number of publications in 2022 decreased slightly, it increased significantly, reaching 6166. In the first quarter of 2023, the number of publications and citations has reached 92 and 2163, and at this speed, the annual number of publications and citations should exceed 400 and 7000. This indicates that the topic of price forecasting is becoming more and more attention year by year, which is related to the increasing uncertainty of global economic development and the intensification of fluctuations in various commodity prices, seriously affecting the normal development of the economy. At the same time, the high citation also indicates that the research topic of price prediction has not only attracted more and more researchers’ attention but also provided a foundation for related research.

The specific citations of these articles are shown in

Table 1. The citations of articles.

	Citing Articles	Times Cited	H-Index
total	16,125	21,613	59
Without self-citations	15,173	19,455
Average per item		9.2

.

As can be seen from Table 1, these articles were cited a total of 21,613 times, with an average of 9.2 times. A total of 15,173 articles cited the views of these articles, including 59 highly cited articles. This not only shows that the level of these articles is relatively high but also shows that, as the main means to ensure market stability and policy intervention, price forecasting has become an important reference for other studies.

The details of the five articles with a high citation rate are shown in

Table 2. Specific details of five H-cited articles.

Articles Information	Citations Information
	Previous Year			Per Year	Total
	2023	2022	2021
Deep learning for finance: deep portfolios Heaton, J.B.; Polson, N.G; Witte, J.H. Jan-feb 2017 | 33 (1), pp.3–12 APPLIED STOCHASTIC MODELS IN BUSINESS AND INDUSTRY	11	45	44	30	210
A CNN-LSTM model for gold price time-series forecasting Livieris, I.E; Pintelas, E; Pintelas, P. Dec 2020|32 (23), pp.351–360 NEURAL COMPUTING & APPLICATIONS	18	104	54	46.25	185
Investor Attention and Stock Market Volatility Andrei, D.; Hasler, M. Jan 2015|28 (1), pp.33–72 REVIEW OF FINANCIAL STUDIES	30	41	47	19.89	179
Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series Ribeiro, M.H.D.; Coelho, L.D. Jan 2020|86 APPLIED SOFT COMPUTING	22	68	57	43.5	174
Interaction between oil and US dollar exchange rate: nonlinear causality, time-varying influence and structural breaks in volatility Wen, F.H.; Xiao, J.H.; et al. 2018|50(3), pp.319–334 APPLIED ECONOMICS	5	24	32	25	150

.

From Table 2, it can be seen that the research on price predication has strong applicability. From the title of the article, it can also be seen that these highly cited articles involve multiple fields such as finance, gold, stocks, energy, agricultural products, etc. It indicates that price forecasting issues in various fields have attracted widespread attention, especially in the financial field, which represents a barometer of the product market; gold and energy, which are influenced by both economic and political factors; and bulk agricultural commodities, which are influenced by multiple factors such as economy and weather. The price fluctuations of these products are characterized by strong uncertainty and volatility.

2.2.2. Recognized by the Chief Editors of Many Publications

In terms of publication title, these articles are distributed in 486 publications. It can be seen that many journals’ editors and reviewers are very interested in this topic. The distribution of the top 10 journals in terms of publication volume is shown in Figure 5. Among the top 10 journals, six belong to the field of mathematics and it applications, with 99 articles published in Mathematical Problems in Engineering, accounting for 4.22% of the total publication entries. A total of 49 articles were published in Mathematics, accounting for 2.09%, showing that the application of mathematical models to price forecasting has been recognized by experts in the field of mathematics. A total of 86 and 49 articles were published in Quantitative Finance and Energy Economics, respectively. This not only shows the importance of price forecasting in the financial and energy fields but also indicates that price forecasting with mathematical models is recognized by experts in the financial and energy fields. There are also 55 and 42 articles published in Mathematical Finance and SaiM journals on financial mathematics, indicating that this research topic is also a hot topic in the application of financial mathematics.

2.2.3. Wide Geographical Distribution

From the distribution of researchers’ countries/regions, it can be seen that the authors of these articles are widely distributed in 100 countries/regions worldwide, indicating that this research topic is of a global nature and has attracted the attention of researchers from various countries/regions.

2.3. Keywords Cluster Analysis

Currently, many complex models are used for data retrieval and literature analysis, such as Citespace, CNN, etc., to realize the visualization and ensure that the analysis is more accurate and easier to understand. ensuring more accurate and understandable analysis. Rehman et al. (2019) [13] provide a comprehensive survey of the relationship between CNN with different pre-trained learning methodologies and its optimization effects and further develop the state-of-the-art algorithms in recognition, classification, and detection of images, speeches, texts, and videos. In this part, VOSviewer was used to cluster the density and network relationships of keywords in these 2349 articles.

2.3.1. Density Analysis

Using VOSviewer for density analysis, the results are shown in Figure 6.

In Figure 6, it can be seen that in addition to high-frequency words such as model, forecasting, and prediction, the main research methods used in mathematical models, especially those involving complex systems, such as NN (neural-network), decomposition, ML (Machine learning), DP (deep learning), ISTM, ARIMA, and Regression, also appear in high-density hot words, indicating that many classical mathematical models are used for price prediction.

Secondly, words such as Chaos, spectrum, spiders, time series, uncertainty, noise, variance, jump, vix, dynamic, and stochastic, which represent the characteristics of price fluctuations, also appear in high-density hot words, indicating that price fluctuations have complex characteristics such as extremely strong uncertainty, greatly increasing the difficulty of prediction. On the other hand, it also indicated that when making price predictions, these features are being incorporated into the model as much as possible to improve the accuracy of the prediction.

Thirdly, energy, crude oil, crypto-currency, bitcoin, gold, stock, and exchange rate appear in the high-density hot words, indicating that these commodities are the key research fields of price prediction. The reason is that the price of these commodities fluctuates more violently than other general commodities. The characteristics of Chaos, uncertainty, etc. are more obvious, which makes it more difficult to accurately predict the price fluctuation trend of these commodities. More complex mixed models are needed to improve the accuracy of prediction. Therefore, it has attracted more attention, and many researchers hope to improve the prediction accuracy of these commodities through complex mathematical models and provide a more accurate basis for decision-makers.

Fourthly, spot, futures, and option also appeared in the high-density hot words, among which future and option appeared more frequently than spot, indicating that researchers not only pay attention to the price fluctuations in the spot market but also pay more attention to the price fluctuations of futures and options. Futures and options were originally designed as a hedge against risk, but now they have become a tool for many people to speculate, making them more volatile. In addition, because the actual occurrence time of these two prices is far from the initial transaction and forecast time, they are more difficult to predict than the spot market price, so they have attracted more researchers’ attention.

Fifth, keywords such as optimization, accuracy, equilibrium, and efficiency, which represent the results pursued in price forecasting, also appear in high-density hot words.

2.3.2. Network Analysis

As can be seen from Figure 7, volatility, model, option, predication, and optimization, etc. are all key connection points in the network. This part will focus on the analysis of these words.

1.

Volatility and Stochastic Volatility

As important features of price fluctuations, volatility and stochastic volatility are important bridges linking related research. Most research focused on this topic; almost all of the aforementioned high-density words are related to these two words, as shown in Figure 8.

2.

Model, time-series, and algorithm

The model is a method of price prediction. No matter what commodity price prediction is made, it cannot be separated from the use of a model. Therefore, the keyword network associated with the model is almost consistent with the entire keyword network diagram, as shown in Figure 9. It can also be seen that various research methods, such as NN, GARCH, and ISTM, and commodity categories, such as gold, oil, and bitcoin (the high-density words appear above), are almost all related to the model.

As two major types of price prediction methods, time-series and algorithms are associated with many research methods, as shown in Figure 10.

At the same time, there is also a strong correlation between these two methods. Because it is difficult to use a single model to effectively describe and express the complexity of price fluctuations. Many hybrid models are used to predict price fluctuations; they can not only identify the chaotic characteristics of time-series data but also solve nonlinear problems. It has better prediction accuracy than a single model and has been widely used. For example, Chen et al. (2022) [14] used the ELM model to predict the non-stationary trend series, while the high-frequency series and low-frequency series are predicted using ARMA after using the EEMD method to decompose the carbon futures price into two IMF (intrinsic mode functions) and a residual and using the FE (fuzzy entropy) and K-means clustering method to reconstruct the IMF and the residual. Liu et al. (2022) [15] integrated ARIMA, GARCH, BPNN, LSTM, and SVM to predict the carbon price on the basis of three interval-based multi-scale decomposition methods: IDWT, IEMD, and IVMD.

3.

Forecasting and Predication

As the main research objectives, forecasting and prediction are also hot topics in the research networks. In terms of prediction behavior, these two words are more associated with specific prediction methods, such as ARIMA, Machine Learning, wavelet transform and big date, as shown in Figure 11. These two words are also associated with volatility, indicating that no matter what kind of forecasting method is adopted, it is necessary to consider the key characteristic of price volatility. Both words are also associated with the Market, indicating that the behavior of forecasting is aimed at mitigating the wild fluctuations of market prices.

4.

Return, optimization, and risk

Investors pursue a high rate of return, and model often pursues the optimal state. The essence of price prediction is to express various factors affecting price fluctuation with suitable parameters, and realize accurate prediction of price fluctuation trends through various complex mathematical models, so as to find the key risk points, avoid investment risks and achieve high investment returns. Therefore, the keywords return, optimization and risk are three aspects that need to be considered in price prediction, among which the identification of risk is the connection point to realize the optimal model and the high return in reality, as shown in Figure 12.

5.

Options and option-pricing

As an important tool for avoiding the risk of income fluctuations caused by price fluctuations, options have received dual attention from both the theoretical circle and industry sectors. The prediction of option prices is also one of the key topics in the field of price prediction. Therefore, options and option pricing are also hot topics in the research network, as shown in Figure 13. As different options pricing methods appear, American options, European options, and Asian options all appear in the related network of this hot word.

6.

Stock, gold, and Crude oil

The financial market is naturally chaotic and uncertain. The accurate prediction of financial asset prices can increase investors’ returns. Therefore, forecasting fast-fluctuating and high-frequency financial data has long been a focus of economic research. Due to the complexity of the stock market, such as its noisy, non-stationary, and heteroscedastic structure, price prediction is always a challenging problem (Mahmoodi et al., 2022 [16]).

Gold price fluctuations have always attracted the attention of governments, institutions, and individuals. As a precious metal, gold is not only widely used in jewelry, investment, and industrial applications but is also regarded as a safe haven for hedging fluctuations, such as an inflation hedging tool and a hedging tool to avoid exchange rate fluctuations (Wen and Cheng, 2018 [17]). However, due to the fact that gold price fluctuations are often influenced by various factors, including market demand, supply, monetary policy, and geopolitical risks, especially in recent years with the increase of uncertain events such as black swans and rhinoceroses, gold price fluctuations have become more violent, the status of hedging tools has been increasingly questioned, and more and more studies have put forward different views. (Choudhry et al., 2015 [18]; Shahzad et al., 2017 [19]; Iqbal., 2017 [20]). Therefore, accurate prediction of gold prices has also become a focus of research.

As the “blood” of the world economy, the price of crude oil is bound to become the focus of global attention. The price fluctuations of crude oil not only have an impact on the energy industry but also have a significant impact on the stability of the entire world’s economic development. The decrease or increase in crude oil prices has a direct impact on economic indicators as well as on stock markets. It has a more direct function of reflecting the economic “barometer”, while the stock index is more of a barometer of money liquidity and asset bubbles (Khalfaoui et al., 2019 [21]). Because the US dollar (USD) is the major invoicing currency for international crude oil trading, changes in the USD exchange rate are considered an important factor in crude oil price fluctuations. The relationship between the dollar and oil prices is also the subject of much research (Wen et al., 2017 [22]).

With the recovery of the world economy, energy demand will further increase. Due to limited crude oil reserves, the supply-demand contradiction will exacerbate price fluctuations. There will be more and more researchers studying the fluctuations of oil prices and the relationship between oil prices and other commodity prices. This also explains why there is an association between crude oil and gold in the network diagram of keywords, as shown in Figure 14.

As the most well-known cryptocurrency, the volatility of bitcoin, which is highly endogenous, highly random, highly risky, and speculative, just like chaos (Baek, 2015 [23]), has attracted the attention of researchers. Research has found that Bitcoin prices have characteristics such as asymmetry, a heavy tail, autocorrelation, etc. (Al-Yahyaee, 2018 [24]; Alvarez-Ramirez, 2018 [25]; Wu and Chen, 2020 [26]). The uncertainty of the global economy provides the possibility that bitcoin becomes a new basket for diversified investment (Demir, 2020 [27]), bringing it closer to general financial products such as oil futures or gold. Therefore, the relationship between bitcoin and other financial assets has attracted the attention of many researchers (Kim et al., 2020 [28]; Zhang and He, 2021 [29]). Bildirici et al. (2022) [30] designed the Markov switching generalized autoregressive conditional heteroskedasticity copula (MS-GARCH—copula) and MS-GARCH-copula-causality method to analyze the regime-dependent and tail dependence among oil, VIX, gold, exchange rates, and BIST stock market returns.

7.

Research method

Based on the complexity of price prediction, many classical and cutting-edge models are used for price prediction, as shown in Figure 15. The next section will summarize and analyze the various models used for price forecasting.

3. Main Research Methods and Analysis

Price forecasting models can be roughly divided into two main categories: one type is based on econometric methods, another is based on algorithms. The model based on econometrics has the advantage of capturing the characteristics of time-varying price fluctuations but cannot accurately describe the nonlinear characteristics of price fluctuations. Compared with the first type of model, the second type of model has a stronger ability to handle nonlinear data and is more widely used in the field of price prediction.

3.1. The Prediction Models Based on Econometrics

The prediction models based on econometrics are further divided into two types. One is the time series prediction model, including AR (Autoregressive), ARCH (Autoregressive conditional heteroskedasticity model), ARIMA (Autoregressive Integrated Moving Average), ARFIMA (autoregressive fractional integrated moving average, Bukhari et al., 2020 [31]), GARCH (Generalized ARCH, Qureshi et al., 2020 [32]), GARCH expansion (Kristjanpoller and Minutolo, 2018 [33]), etc. For example, Segnon et al. (2017) [34] extended the GARCH model to a model with long-term dependence and institutional transformation, realizing the simulation and prediction of the dynamics of carbon prices. Huang et al. (2021) [35] used the GARCH model to predict the high-frequency sub-mode of carbon prices. However, this type of model does not consider other factors and only relies on historical prices for prediction.

Another is structural models, such as ECM (Error Correction Model), VECM (Vector ECM), and VAR (Vector Autoregressive). These models use linear regression to process data, and influencing factors can include not only historical price data but also corresponding exogenous variables. The model setting mainly involves using historical price data as regression variables and using linear combinations of random variables from early stages to describe the characteristics of random variables at a certain future time. It is widely used in various predictions and analyses. Price data, as a time series with strong autocorrelation, can obtain satisfactory forecasting results using these methods to analyze its internal characteristics. For example, Hammoudeh et al. (2015) [36] analyzed the short-term dynamic effects of carbon prices on the price changes of oil, coal, natural gas, and electricity by using VAR and VECM.

Although these models have some shortcomings, the number of citations is still high. Among them, the cited times of Hammoudeh et al. (2015) are close to 100. Segnon et al. (2017) have also been cited more than 50 times. Indicating that these methods are all very classical methods that have been recognized by the academic circle and widely applied. At the same time, it can be seen from the following analysis that many hybrid models have also applied these methods as one of their basic methods.

3.2. Prediction Models Based on Algorithms

In order to alleviate the influence of nonlinear fluctuations in price series on the prediction results, a machine learning model has also been introduced to solve the complex nonlinear problems.

3.2.1. Decomposition-Integration Method

This kind of method mainly includes LCD, MS, PSR, WT, HP analysis, EMD, VMD, etc., as shown in

Table 3. Decomposition-integration method.

Research Methods	Meaning
Local Characteristic Scale decomposition, LCD	Adaptively decompose a complex signal into the sum of several Intrinsic scale component (ISC) with physical significance
Multi-Scale, MS	Provide a bridge for data at different lengths and time scales, enabling models suitable for different scales to communicate with each other.
Phase Space reconstruction, PSR	A method for recovering and characterizing a prime mover system from a known time series.
Hodrick–Prescott, HP	Determine long-term trends of time series by discounting the importance of short-term price fluctuations.
Wavelet transform, WT	By transforming, fully highlighting the characteristics of some aspects of the problem, locally analyze the time (space) frequency. The signal (function) can be gradually refined at multiple scales through scaling and translation operations, ultimately achieving time subdivision at high-frequencies and frequency subdivision at low-frequencies, which can automatically adapt to the requirements of time-frequency signal analysis, thus focusing on any details of the signal.
Empirical Mode Decomposition, EMD	The signal is decomposed according to the time scale characteristics of the data itself, without setting any basis function in advance. The essence is to identify all vibration modes contained in the signal through the characteristic time scale.
Variational mode decomposition, VMD	An adaptive and completely non recursive method for modal change and signal processing. By iteratively searching for the optimal solution of the variational problem, determining the frequency and bandwidth of each decomposed component, realize the effective separation of the natural mode components, and ultimately obtaining the optimal solution of the variational problem.

. This kind of model can decompose the original complex time series at multiple scales and transform it into simple and easy-to-analyze submodules, which is conducive to the suggestion and analysis of the model and has been verified as an efficient time series prediction method. For example, Sun et al. (2018) [37] used WT to eliminate the high-frequency components of the carbon price data of the previous day to enhance the prediction accuracy.

Sun and Zhang (2022) [38] decomposed the carbon price into several ISC through LCD to obtain their characteristics and then predict.

Among the data decomposition methods, EMD and its extension method are the most popular. EMD does not need any pre-defined primary functions, is adaptive, and is a completely data-driven, unsupervised signal decomposition method. EMD reconstructs the original signal into decomposition modules of different frequencies by reconstructing signal data into IMFs and residual terms. This method is not only applied in the field of price prediction but also performs well in the fields of the wind speed, traffic load, power load, and so on. In order to reduce the end effects and mode aliasing problems that may exist in EMD methods, researchers have made a lot of improvements to them. More suitable models for price prediction are designed, such as EEMD (Ensemble EMD, Chen et al., 2022 [14]), MEEMD (Modified Ensemble EMD, Yang et al., 2020 [39]), ICEEMD (Improved Complete Ensemble EMD, Ji et al., 2022 [40]), CEEMDAN (the extension of EMD, Zhang et al., 2022 [41], etc.).

In addition to EMD, the non-recursive VMD method has also been widely applied in the prediction field in recent years due to its insensitivity to noise and more rigorous theoretical basis (Zhu et al., 2019 [42]). Chai et al. (2021) [43] used the VMD to decompose the carbon price data and used sample entropy to reconstruct the decomposed sequence.

Due to the nonlinear, non-stationary, and uncertain price series, many research methods are continuously optimized to improve the accuracy and stability of predictions. Liu et al. (2022) [15] further optimized the above decomposition methods on the basis of previous studies, proposed a hybrid prediction model based on mixed interval multi-scale decomposition, and developed three interval multi-scale decomposition methods. Including the IDWT (Interval DWT), IEMD (Interval EMD), and IVMD (Interval VMD) methods, decompose interval value carbon price into interval trend and residual.

3.2.2. Machine Learning Model

ML is a multi-disciplinary cross-specialty, covering Probability theory, statistics knowledge, approximate theory, complex algorithms, and other knowledge. It realizes the automatic improvement of algorithms by simulating human learning methods. At present, both traditional ML algorithms such as KL (kernel Learning), RF (Yang et al., 2020 [39]), PSO, and DN models, including ANN (Gocken et al., 2016 [44]; Montri et al., 2016 [45]; Reza et al., 2015 [46]), that are closer to AI, are widely used for price forecasting.

For example, Li et al. (2020) [47] used BPNN to simulate the long-term trend of carbon futures price changes under six scenarios, considering factors such as energy prices and stocks of clean companies. Atsalakis and George (2016) [48] used three computational intelligence technologies to provide accurate and timely prediction of carbon price changes, including a closed-loop feedback mechanism called PATSOS, an ANN-based system, and ANFIS. Zhang and Ci (2020) [49] used the DBN model to forecast the gold price. Weng et al. (2020) [50] proposed a GA-ROS-ELM (genetic algorithm regularization online ELM) to predict gold price data collected from public websites. Mahmoodi et al. (2022) [16] combined the SVM-PSO to predict the stock price.

Figure 16 shows some ML algorithms in price forecasting and their logical relationships. The specific meanings of some commonly used algorithms are shown in

Table 4. Machine learning model.

Research Methods	Meaning
Support Vector Machine, SVM	A kind of generalized linear classifier that classifies data binary according to supervised learning.
Support Vector Machine, SVR	SVR is an important branch of SVM. By SVR, a regression plane can be found and the distance between all data in a set and the plane can be minimized.
Least square support vector machine, LSSVM	A kernel function learning machine following the principle of structural risk minimization (SRM).
Random Forest, RF	Refers to a classifier that uses multiple trees to train and predict samples.
A convolutional neural network, CNN	Imitate human vision and can effectively reduce the dimensionality of a large amount of data into a small amount of data without affecting the result.
Artificial Neural Network, ANNs	Intelligent and nonparametric mathematical models inspired by the biological nervous system, realizing the purpose of processing information by adjusting the interconnection between a large number of internal nodes.
Feedforward neural network, FNN	The simplest kind of neural network in which neurons are arranged in layers, and each neuron is only connected to the neurons in the previous layer.
Extreme Learning Machine, ELM	A kind of machine learning system or method based on FNN.
Back propagation neural network, BPNN	Add the backward propagation algorithm to the structure of feedforward network.
The adaptive neuro-fuzzy inference system, ANFIS	A type of fuzzy reasoning system structure that organically combines fuzzy logic and neural network and adopts the mixed algorithm of back propagation algorithm and least square method to adjust the premise parameters and conclusion parameters.
Deep belief network, DBN	A probabilistic generative model composed of multiple simple learning modules
Recursive neural network, RNN	Which takes sequence data as input, recursion in sequence evolution direction, and all nodes (cyclic units) are connected by chain
Long Short-Term memory, LSTM	By improving the gradient propagation process of the RNN model, it can alleviate the phenomenon of gradient disappearance of words far away from the end of the sentence is easy to occur in the reverse propagation process.
Gated Recurrent Units, GRU	The gating mechanism of the introduced recurrent neural network, which belongs to the variant of LSTM.
Particle Swarm Optimization, PSO	Simulate the swarm behavior of animals, such as insects, birds, and fish. These animals swarm and seek food in a cooperative manner. In order to achieve optimal results, each member of the swarm constantly changes search mode by learning experiences of itself and other members.

.

Kumar and Haider (2020) [51] used the RNN–LSTM network integrated with a metaheuristic optimization technique to predicate stock price to enhance the intra-day stock market prediction. Zhou et al. (2022) [52] combined VMD-CEEMDAN to decompose the carbon price sequence and then used the RNN optimized by LSTM to predict. Vidal and Kristjanpoller (2020) [53] combined two DP methodologies, LSTM and convolutional NN, to improve the forecast of gold volatility.

3.2.3. Animal Algorithm

Animal algorithms also belong to ML, they are the metaheuristic optimization algorithms, but they are all designed by imitating animal foraging behavior and named by animal names, so here we temporarily call them animal algorithms. Mainly including ACO (Ant Colony Optimization), FFO (Fruit Fly Optimization), AFSA (Artificial Fish Swarms Algorithm), BOA (Bat Optimization Algorithm), GOA (Grasshopper Optimization Algorithm), GWO (Gray Wolf Optimization), SSA (Sparrow Search Algorithm, Zhou and Chen, 2021 [54]; Sun and Zhang, 2022 [38]; Ji et al., 2022 [40]), WOA (Whale Optimization Algorithm), etc. The foraging behavior of these animals basically has a common feature: it is seemingly chaotic, but in fact there are certain rules. That are similar to the chaotic characteristics of prices, so many researchers use animal algorithms to simulate and predict the nonlinear complex system by simulating the seemingly irregular but actually regular behavior of animals, especially price prediction. Sahoo and Mohanty (2020) [55] applied the GWO technique to tune the parameters of ANN for forecasting the stock price of the BSE (Bombay Stock Exchange) for one day, fifteen days, and thirty days ahead.

Taking FFO and WOA as examples to illustrate the application of animal algorithms in the field of price prediction.

• FFO

The FFO Algorithm is a method for finding global optimization based on the food-finding behavior of the fruit fly. The fruit fly itself is superior to other species in sensing and perception, especially in apheresis and vision, as shown in Figure 17. The apheresis organs of fruit flies can find all kinds of scents floating in the air; they can even smell food sources from 40 km away. Then, after it becomes close to the food location, it can also use its sensitive vision to find food and the company’s flocking location and fly in that direction too (Pan, 2012) [56].

Gowthul et al. (2019) [57] developed a parameter tuning approach using the FFO algorithm to forecast stock prices.

2.

WOA

WOA is inspired by the hunting behavior of humpback whales, which is termed the bubble-net hunting strategy. These whales use two mechanisms for searching for the location of prey and subsequently attacking it, as illustrated in Figure 18.

They initially encircle the prey and eventually create bubble nets. In view of an optimization point, the exploration of search space is achieved when the whales look for prey, and exploitation occurs during the attack behavior. The major difference between WOA and other algorithms lies in the rules that improve the candidate solutions at every step of optimization. Zakaria et al. (2019) [59] used WOA as a trainer to learn the multilayer perceptron NN to forecast long-term gold price fluctuations.

4. Analysis of Hybrid Models for Price Forecasting

Although numerous classic econometric and various machine learning methods are utilized to predict prices. Nevertheless, the chaotic characteristics of price series are difficult to effectively describe and express with a single model. Therefore, many researchers use a hybrid method to make predictions. This section will take some product price predictions as an example to analyze the basic modeling ideas and main research method combinations of hybrid models.

4.1. Crude Oil Price

According to the previous keyword cluster analysis, oil prices are an important branch in the field of price prediction. Many hybrid models are used to forecast oil prices. For example, EEMD-LSSVM-PSO-GARCH (Zhang et al., 2015 [60]), GA-NN (Chiroma et al., 2015 [61]), DL-CNN (Li et al., 2018 [62]), etc. AI algorithms based on the ANN-LSSVR model by using Compressed Sensing-based Denoising (CSD) were used to filter out the noises in the crude oil price data (Yu et al., 2015 [63]). Yu et al. (2017) [64] compared five methods, including SVM, FNN, ARIMA, ARFIMA, and MS-ARFIMA (Marv-Switching ARFIMA). Finding that SVM has the highest prediction accuracy. Elaziz et al. (2019) [65] improved the ANFIS model by using the GA (genetic algorithm) and a modified SSA to predict crude oil prices.

4.2. Stock-Market Price

Stock trend forecasting has gained significant attraction due to its prospective economic benefits (Vanguri et al., 2022 [66]). However, concerning its various interrelated factors, stock market prices are dynamic, highly sensitive, nonlinear, and chaotic, stock forecasting remains a challenging task. It requires an effective prediction technique for determining the most informative factors; hybrid models have better prediction performance, such as ANN-GA (Montri et al., 2016 [45]), BNN (bat-NN)-MAS (multi-agent system, Reza et al., 2015 [46]), DPSO (discrete PSO)/PSO-FFNN (feed-forward NN, Kumar et al., 2022 [51]), APSO (adaptive PSO)-LSTM (Kumar et al., 2022 [67]), and ARFIMA-LSTM (Bukhari et al., 2020 [31]).

4.3. Cardon Price

Some countries have formulated carbon neutrality plans to deal with global warming, and these plans have derived various carbon trading markets. All parties involved in carbon trading hope to obtain the maximum benefits from it; the carbon trading price is crucial to both sellers and purchasers, which requires participants to accurately determine the price of carbon trading (Wang and Qiu, 2022 [68]; Ma and Wang, 2022 [69]; Cao and Liu, 2023 [70]). Therefore, carbon price forecasting is also a research hotspot in the field of price forecasting.

For example, Qin et al. (2022) [71] used the HP filter to identify the repetitive upper and lower structural features around a specific carbon price, conducted a preliminary decomposition of carbon prices, and then used multi-scale decomposition to decompose the residual term so as to obtain more accurate carbon price prediction results from the EU ETS. It has certain competitive advantages in terms of prediction accuracy and time cost. Li et al. (2020) [72] used the BPNN model optimized by the average impact algorithm to determine the main influencing factors of the carbon price, simulate the change trend of the carbon price under different economic development and energy consumption levels, and help the government realize advance planning and formulate various countermeasures. Ren et al. (2022) [73] selected prediction factors and forecast carbon price and carbon futures income through the dimensionality reduction mechanisms of LASSO (Least absolute shrinkage and selection operator) and SCAD (Smoothly Clipped Absolute Deviation) models. The research found that this mixed model is superior to many other models in terms of forecasting accuracy. In addition, many other hybrid models are used to forecast oil prices, such as VMD—EMD-PSO (Cui et al., 2022 [74]), VMD-LSTM (Wang and Qiu, 2022 [68]), and CEEMDAN-PE (permutation entropy)-LSTM-RVM (Yang et al., 2022 [75]).

Wang et al. (2022) [76] established a VMD-ELM-SSA model, as shown in Figure 19. Firstly, use the improved VMD to decompose data, in which CF (center frequency) and MI (mutual information) are introduced to determine the number of decomposition layers comprehensively. Secondly, introduce MSE (multiscale entropy) to measure the complexity of each IMF; moreover, a threshold is set to classify the IMF. The IMFs with more noise are classified into one category, and the remaining are classified into another. Thirdly, the SSA is introduced to optimize the above parameters of the ELM model and give full play to the advantages of ELM in nonlinear data sets. Specifically, after ELM is optimized by SSA, its initial threshold can more easily adapt to the original data, so the prediction results are more accurate.

4.4. Summary of Modeling Ideas

According to the above analysis, it can be seen that no matter what price is predicted, these hybrid models can be roughly divided into three categories: Decomposition + Machine Learning; Decomposition + Regression + Machine Learning; and Decomposition + Animal Algorithm + Machine learning. And for either combination, the decomposition model is used. Basically, the complex price sequence is first broken down into a relatively simple sequence, which is then predicted by various algorithms.

4.4.1. Decomposition + Machine Learning

The prediction idea of these articles is basically to decompose the price sequence using VMD or EMD, or their combination (Sun and Huang, 2020 [77]), or their extended combination, and then predict, as shown in Figure 20.

Some researchers also conduct chaotic feature analysis before data decomposition. For example, Tian and Hao (2020) [78] used the MLE to carry out chaos analysis on the price sequence before using VMD to decompose, and then the reconstructed sequences by PSR technology were used as the optimal input and output variables of the prediction model. Finally, an ANFIS was used to point out the prediction of carbon prices. Based on the distribution function of price series determined by point prediction results and analysis module, the interval prediction is realized.

Zhu et al. (2019) [79] proposed a VMD-CCI (comprehensive contribution index), MR (modes reconstruction), and CFM (optimal combined forecasting model), the major steps of method are shown in Figure 21.

4.4.2. Decomposition + Regression + Machine Learning

The idea of building prediction models in these articles is similar to the one above. Basically, VMD or EMD, or their combination, or their extended combination, are used to decompose price sequences, and then regression and machine learning are used to predict different sequences, as shown in Figure 22. For example, Huang et al. (2021) [35] used the LSTM network to predict low-frequency sub-patterns, used the GARCH model to predict high-frequency sub-patterns, on the basis of using VMD to decompose carbon valence, and then integrated the prediction from sub-patterns through the LSTM nonlinear integration method. The empirical results show that the model is very suitable for predicting the carbon price rise in the later stage of the third stage of the EU ETS, providing participants with a good insight into risk aversion.

Wang et al. (2021) [80] constructed a model that combines optimal feature reconstruction and biphasic DL to predict carbon prices, which DRNN (Deep RNN)-GRU is used to predict after using VMD-SE to extract different features from the original carbon price effectively. Similarly, on the basis of decomposing and reconstructing the original price sequence by using VDM-SE, Chai et al. (2021) [43] predicted the subsequence by using the ELM optimized by particle PSO.

4.4.3. Decomposition + Regression + Animal Algorithm + Machine Learning

Similarly, chaos feature recognition and decomposition of price sequences are also carried out in this kind of mixed model. The difference is that the animal algorithm is used in these articles to optimize the ML algorithm before price prediction is carried out, as shown in Figure 23.

The optimization and combination of the two algorithms make the prediction more accurate. For example, Yang et al. (2020) [39] decomposed the MEEMD into nine IMFs and a residual and used LSTM optimized by the IWOA to predict carbon prices.

Sun et al. (2018) [36] applied the PACF (partial auto-correlation function) to analyze the correlation among historical carbon prices to select the inputs for the forecasting model, on the basis of using WT to eliminate the high-frequency components of the previous day’s carbon price data to improve the accuracy of prediction, and then used BOA to optimize the parameters of the K-ELM model to predict the carbon price. Sun and Zhang (2022) [38] used MLE to detect the chaos of the intrinsic scale component on the basis of LCD decomposition carbon price, and the chaotic ISC is further reconstructed by PSR. At the same time, the influence variables of non-chaotic ISC are also selected by PACF. Then the LSSVM optimized by AFSA is established to predict the ISC components of the carbon price series, and the ISC components are combined into carbon price prediction results.

Zhou and Chen (2021) [54] also reconstructed the data according to the Lempel-Ziv complexity algorithm on the basis of obtaining the IMF and a residual from the original data decomposed by ICEEMDAN and determined the input variables of the model through the PSR algorithm combined with PACF. Then SSA was used to optimize the ELM model for carbon price prediction. Similarly, Ji et al. (2022) [40] used SSA to optimize the BPNN for point prediction of carbon price and combined the KDM (kernel density estimation) method to achieve interval prediction of carbon price. Zhang et al. (2018) [81] used ACA to optimize the GNN (Grey NN) to predict the carbon price.

From the above, it can be seen that no matter what kind of combination there is, the basic idea is to decompose the complex price series before reconstruction and then use various algorithms for prediction and integration.

The decomposition-reconstruction-prediction-integration strategy is an effective method to predict the price.

5. Research Conclusions and Outlook

Due to the complexity, nonlinearity, and instability of price fluctuations, many classical and advanced mathematical models have been used in price prediction (Ma, 2020–2021–2023 [2,82,83]). Compared with the single model, the hybrid model can provide more accurate prediction results. However, there is still room for improvement in prediction accuracy. How to select effective model combinations to further improve the accuracy of price prediction is the direction of future research.

As a breakthrough in AI technology, LLM (Language Model for the World) has become the darling of numerous researchers. LLM is a giant Natural language processing (NLP) model launched by Google in 2019. It is a neural network with a large number of parameters (one billion or more) and has achieved leading performance on a number of NLP tasks. In 2022, OpenAI released the application of ChatGPT based on GPT-3 technology, which shocked the entire industry with its large model effect. Using LLM for price prediction should also significantly improve prediction accuracy and achieve breakthroughs in the field of price prediction. Therefore, the use of LLM for price prediction will be an important research direction in the future.

For the research object, use VOSviewer to analyze the timeline of keywords, as shown in Figure 24.

It can be seen that future economic growth is facing instability, uncertainty, and complexity, and price fluctuations such as energy and gold have been the focus of research. At the same time, the emergence of cryptocurrencies, especially Bitcoin, has changed the wealth structure of many people, and cryptocurrency price fluctuations have become an important research object.

Due to more and more extreme weather brought about by environmental change, destructive power is also growing. How to protect the ecological environment and achieve sustainable economic growth is a concern for all governments. As an important means of protecting the environment, carbon emission trading has been recognized by more and more countries and enterprises, so carbon price prediction will also be an important direction of future research.