Numerical Approach of the Equilibrium Solutions of a Global Climate Model
Abstract
:1. Introduction
2. The Energy Balance Model (EBM)
3. The Coupled Model: Deep Ocean-EBM
- (H1)
- is a bounded maximal monotone graph of , such that there exist two constants and , such that if , if .
- (H2)
- S() and a.e.
- (H3)
- .
- (H4)
- The constants B, A, R, Q, , , and are positive.
Stationary Model
4. Numerical Resolution
4.1. Spatial WENO Reconstruction
- One central stencil: ,
- One fully biased to the left stencil: , , ,
- One fully biased to the right stencil: , , ,
- Two central stencils: , , and , ,
- One left-sided stencil: , , ,
- One right-sided stencil: , , .
4.2. Time Integration
- For the solution in the surface (EBM)where is the discrete operator, whose expression is given in (19) and refers to the cell average of the solution for the 1D control volume i at time .
- For the deep ocean, we havewhere is the discrete operator, whose expression is given in (23) and refers to the cell average of the solution for the control 2D volume at time .
5. Results
| Algorithm 1 Marching in time up to stationary solution |
| 1: while do |
| 2: Prescribed , |
| 3: for to N do |
| 4: while do |
| 5: Compute |
| 6: |
| 7: |
| 8: |
| 9: end while |
| 10: end for |
| 11: Increment the value of Q |
| 12: end while |
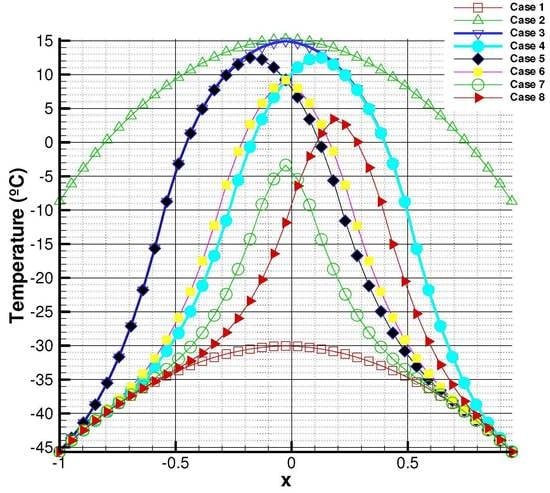
5.1. Non-Coupled Model
- Case 1:
- Case 2:
- Cases 3–6:
- Case 7:
- Case 8:
5.2. Coupled Model
6. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EBM | Energy Balance Model |
| DOM | Deep Ocean Model |
| TVD | Total Variation Diminishing |
| WENO | Weighted Essentially Non Oscillatory |
| RK | Runge-Kutta |
| RK3-TVD | Third order Runge-Kutta TVD |
| FV | Finite Volume |
| FTCS | Forward in Time Centred in Space |
| ODE | Ordinary Differential Equation |
| PDE | Partial Differential Equation |
| ADER | Arbitrary high order DErivative Riemann problem |
| CFL | Courant-Friedrichs-Lewy |
References
- Budyko, M.I. The effect of solar radiation variations on the climate of the Earth. Tellus 1969, 21, 611–619. [Google Scholar] [CrossRef] [Green Version]
- Sellers, W.D. A Global Climatic Model Based on the Energy Balance of the Earth-Atmosphere System. J. Appl. Meteorol. 1969, 8, 392–400. [Google Scholar] [CrossRef]
- Díaz, J.I. On the mathematical treatment of energy balance climate models. In The Mathematics of Models for Climatology and Environment; Díaz, J.I., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 217–251. [Google Scholar]
- North, G.R. Multiple solutions in energy balance climate models. Palaeogeogr. Palaeoclimatol. Palaeoecol. 1990, 82, 225–235. [Google Scholar] [CrossRef]
- Hetzer, G. The structure of the principal component for semilinear diffusion equations from energy balance climate models. Houst. J. Math. 1990, 16, 203–216. [Google Scholar]
- Díaz, J.; Hetzer, G.; Tello, L. An energy balance climate model with hysteresis. Nonlinear Anal. Theory Methods Appl. 2006, 64, 2053–2074. [Google Scholar] [CrossRef]
- Ghil, M.; Childress, S. Topics in geophysical fluid dynamics atmospheric dynamics, dynamo theory, and climate dynamics. In Applied Mathematical Sciences; Springer: New York, NY, USA, 1987. [Google Scholar] [CrossRef]
- Watts, R.G.; Morantine, M. Rapid climatic change and the deep ocean. Clim. Chang. 1990, 16, 83–97. [Google Scholar] [CrossRef]
- Díaz, J.I.; Tello, L. A nonlinear parabolic problem on a Riemannian manifold without boundary arising in climatology. Collect. Math. 1999, 50, 19–51. [Google Scholar]
- Diaz, J.I.; Tello, L. A 2D climate energy balance model coupled with a 3D deep ocean model. Electron. J. Differ. Equ. 2007, 16, 129–135. [Google Scholar]
- Bermejo, R.; Carpio, J.; Diaz, J.; Tello, L. Mathematical and numerical analysis of a nonlinear diffusive climate energy balance model. Math. Comput. Model. 2009, 49, 1180–1210. [Google Scholar] [CrossRef]
- Bermejo, R.; Carpio, J.; Díaz, J.I.; Galán del Sastre, P. A Finite Element Algorithm of a Nonlinear Diffusive Climate Energy Balance Model. Pure Appl. Geophys. 2008, 165, 1025–1047. [Google Scholar] [CrossRef]
- Díaz, J.I.; Hidalgo, A.; Tello, L. Multiple solutions and numerical analysis to the dynamic and stationary models coupling a delayed energy balance model involving latent heat and discontinuous albedo with a deep ocean. Proc. R. Soc. A 2014. [Google Scholar] [CrossRef] [Green Version]
- Hidalgo, A.; Tello, L. A Finite Volume Scheme for Simulating the Coupling between Deep Ocean and an Atmospheric Energy Balance Model. In Modern Mathematical Tools and Techniques in Capturing Complexity; Springer: Berlin/Heidelberg, Germany, 2011; pp. 239–255. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite-Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Godunov, S. A Difference Scheme for Numerical Solution of Discontinuous Solution of Hydrodynamic Equations. Math. Sb. 1959, 47, 271–306. [Google Scholar]
- Toro, E. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Vázquez-Cendón, M. Solving Hyperbolic Equations with Finite Volume Methods; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Harten, A.; Engquist, B.; Osher, S.; Chakravarthy, S.R. Uniformly High Order Accurate Essentially Non-oscillatory Schemes, III. J. Comput. Phys. 1997, 131, 3–47. [Google Scholar] [CrossRef]
- Liu, X.D.; Osher, S.; Chan, T. Weighted Essentially Non-oscillatory Schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef] [Green Version]
- Shu, C. Essentially Non-Oscillatory and Weighted Essentially Non-Oscillatory Schemes for Hyperbolic Conservation Laws. In Advanced Numerical Approximation of Nonlinear Hyperbolic Equations; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Balsara, D.S.; Shu, C.W. Monotonicity Preserving Weighted Essentially Non-oscillatory Schemes with Increasingly High Order of Accuracy. J. Comput. Phys. 2000, 160, 405–452. [Google Scholar] [CrossRef] [Green Version]
- Titarev, V.; Toro, E. Finite-volume WENO schemes for three-dimensional conservation laws. J. Comput. Phys. 2004, 201, 238–260. [Google Scholar] [CrossRef]
- Dumbser, M.; Zanotti, O.; Hidalgo, A.; Balsara, D.S. ADER-WENO finite volume schemes with space–time adaptive mesh refinement. J. Comput. Phys. 2013, 248, 257–286. [Google Scholar] [CrossRef] [Green Version]
- Dumbser, M.; Hidalgo, A.; Zanotti, O. High order space-time adaptive ADER-WENO finite volume schemes for non-conservative hyperbolic systems. Comput. Methods Appl. Mech. Eng. 2014, 268, 359–387. [Google Scholar] [CrossRef] [Green Version]
- Levy, D.; Puppo, G.; Russo, G. Central WENO schemes for hyperbolic systems of conservation laws. ESAIM Modél. Math. Anal. Numér. 1999, 33, 547–571. [Google Scholar] [CrossRef]
- Levy, D.; Nayak, S.; Shu, C.; Zhang, Y. Central WENO schemes for Hamilton-Jacobi equations on triangular meshes. SIAM J. Sci. Comput. 2006, 28, 2229–2247. [Google Scholar] [CrossRef] [Green Version]
- Dumbser, M.; Boscheri, W.; Semplice, M.; Russo, G. Central Weighted ENO Schemes for Hyperbolic Conservation Laws on Fixed and Moving Unstructured Meshes. SIAM J. Sci. Comput. 2017, 39, A2564–A2591. [Google Scholar] [CrossRef]
- Castro, M.J.; Semplice, M. Third- and fourth-order well-balanced schemes for the shallow water equations based on the CWENO reconstruction. Math. Comput. Model. 2019, 89, 304–325. [Google Scholar] [CrossRef]
- Baeza, A.; Bürger, R.; Mulet, P.; Zorío, D. Central WENO Schemes Through a Global Average Weight. J. Sci. Comput. 2019, 78, 499–530. [Google Scholar] [CrossRef]
- Baeza, A.; Bürger, R.; Mulet, P.; Zorío, D. On the Efficient Computation of Smoothness Indicators for a Class of WENO Reconstructions. J. Sci. Comput. 2019, 80, 1240–1530. [Google Scholar] [CrossRef]
- Baeza, A.; Bürger, R.; Mulet, P.; Zorío, D. An Efficient Third-Order WENO Scheme with Unconditionally Optimal Accuracy. SIAM J. Sci. Comput. 2020, 42, A1028–A1051. [Google Scholar] [CrossRef]
- Balsara, D.S.; Garain, S.; Florinski, V.; Boscheri, W. An efficient class of WENO schemes with adaptive order for unstructured meshes. J. Comput. Phys. 2020, 404, 109062. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef] [Green Version]
- Gottlieb, S.; Shu, C.W. Total Variation Diminishing Runge-Kutta schemes. Math. Comput. 1998, 67, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1983, 49, 357–393. [Google Scholar] [CrossRef] [Green Version]
- Cannarsa, P.; Malfitana, M.; Martínez, P. Parameter Determination for Energy Balance Models with Memory. In Mathematical Approach to Climate Change and Its Impacts; Cannarsa, P., Mansutti, D., Provenzale, A., Eds.; Springer INdAM Series; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef] [Green Version]
- Floridia, G. Approximate controllability for nonlinear degenerate parabolic problems with bilinear control. J. Differ. Equ. 2014, 257, 3382–3422. [Google Scholar] [CrossRef]
- Díaz, J.I.; Tello, L. On a climate model with a dynamic nonlinear diffusive boundary condition. Discret. Contin. Dyn. Syst. S 2008, 1, 253. [Google Scholar] [CrossRef]
- Díaz, J.I.; Hernández, J.; Tello, L. On the Multiplicity of Equilibrium Solutions to a Nonlinear Diffusion Equation on a Manifold Arising in Climatology. J. Math. Anal. Appl. 1997, 216, 593–613. [Google Scholar] [CrossRef] [Green Version]
- Hetzer, G. The shift-semiflow of a multi-valued evolution equation from climate modelling. Nonlinear Anal. Theory Methods Appl. 2001, 47, 2905–2916. [Google Scholar] [CrossRef]
- Hetzer, G. The number of stationary solutions for a one-dimensional Budyko-type climate model. Nonlinear Anal. Real World Appl. 2001, 2, 259–272. [Google Scholar] [CrossRef]
- Díaz, J.I.; Tello, L. Infinitely many stationary solutions for a simple climate model via a shooting method. Math. Methods Appl. Sci. 2002, 25, 327–334. [Google Scholar] [CrossRef]
- Arcoya, D.; Diaz, J.; Tello, L. S-Shaped Bifurcation Branch in a Quasilinear Multivalued Model Arising in Climatology. J. Differ. Equ. 1998, 150, 215–225. [Google Scholar] [CrossRef] [Green Version]
- Stone, P.H. A simplified radiative-dynamical model for the static stability of rotating atmospheres. J. Atmos. Sci. 1972, 29, 405–418. [Google Scholar] [CrossRef] [Green Version]
- Díaz, J.I. Mathematical analysis of some diffusive energy balance models in Climatology. In Mathematics, Climate and Environment; Díaz, J.I., Lions, J.L., Eds.; Research Notes in Applied Mathematics n° 27; Masson: Paris, France, 1993; pp. 28–56. [Google Scholar]
- Hidalgo, A.; Tello, L. On a climatological energy balance model with continents distribution. Discret. Continu. Dyn. Syst. A 2015, 35, 1503. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef] [Green Version]
- Cravero, I.; Puppo, G.; Semplice, M.; Visconti, G. CWENO: Uniformly accurate reconstructions for balance laws. Math. Comp. 2018, 87, 1689–1719. [Google Scholar] [CrossRef] [Green Version]
- Toro, E.F.; Millington, R.C.; Nejad, L.A.M. Towards Very High Order Godunov Schemes. In Godunov Methods; Toro, E.F., Ed.; Springer: Boston, MA, USA, 2001; pp. 907–940. [Google Scholar]
- Titarev, V.; Toro, E. ADER: Arbitrary High Order Godunov Approach. J. Sci. Comput. 2002, 17, 609–618. [Google Scholar] [CrossRef]
- Toro, E.F.; Hidalgo, A. ADER finite volume schemes for nonlinear reaction diffusion equations. Appl. Numer. Math. 2009, 59, 73–100. [Google Scholar] [CrossRef]
- Gassner, G.; Loercher, F.; Munz, C.D. A contribution to the construction of diffusion fluxes for finite volume and Discontinuous Galerkin schemes. J. Comput. Phys. 2007, 224, 1049–1063. [Google Scholar] [CrossRef]
- Hidalgo, A.; Tello, L.; Toro, E.F. Numerical and analytical study of an atherosclerosis inflammatory disease model. J. Math. Biol. 2014, 68, 1785–1814. [Google Scholar] [CrossRef] [Green Version]













| Parameter | Value |
|---|---|
| c, | |
| Q | 340 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hidalgo, A.; Tello, L. Numerical Approach of the Equilibrium Solutions of a Global Climate Model. Mathematics 2020, 8, 1542. https://doi.org/10.3390/math8091542
Hidalgo A, Tello L. Numerical Approach of the Equilibrium Solutions of a Global Climate Model. Mathematics. 2020; 8(9):1542. https://doi.org/10.3390/math8091542
Chicago/Turabian StyleHidalgo, Arturo, and Lourdes Tello. 2020. "Numerical Approach of the Equilibrium Solutions of a Global Climate Model" Mathematics 8, no. 9: 1542. https://doi.org/10.3390/math8091542
APA StyleHidalgo, A., & Tello, L. (2020). Numerical Approach of the Equilibrium Solutions of a Global Climate Model. Mathematics, 8(9), 1542. https://doi.org/10.3390/math8091542